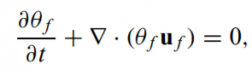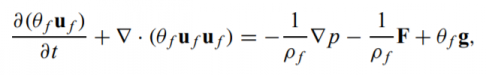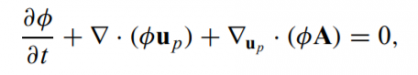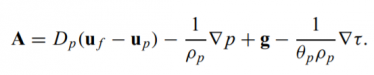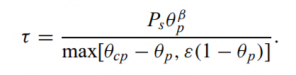Difference between revisions of "Tugas Besar CFD - Josiah Enrico S"
JosiahEnrico (talk | contribs) (→Result and Analysis) |
JosiahEnrico (talk | contribs) (→Result and Analysis) |
||
| Line 114: | Line 114: | ||
[[File:Tugas Besar CFD Mesh1 Jos.png|x500px]][[File:Tugas Besar CFD Mesh2 Jos.png|x500px]] | [[File:Tugas Besar CFD Mesh1 Jos.png|x500px]][[File:Tugas Besar CFD Mesh2 Jos.png|x500px]] | ||
| − | {| class="wikitable" | + | {| class="wikitable" style="width: auto; margin-left: auto; margin-right: auto;" |
|+ style="text-align: center;" | Grid Independent Study | |+ style="text-align: center;" | Grid Independent Study | ||
|- | |- | ||
Revision as of 12:15, 5 January 2021
Contents
Title: CFD Investigation of Dust Particle Elutriation in Plastic Pellet Industry
Abstract
As elutriator, or an apparatus used to separate suspended solid particles according to size, have been used in the plastic industry regarding dust particles such as streamer or angel hair elimination, there is a need to observe the effectiveness of this control process to produce cleaner plastic pellet. In doing so theoretically, some recent studies show differences in particle size are exploited when they are subjected to an upward flowing current of fluid, leading to separation into size-based underflow and overflow streams. The tendency of a particle to report to either stream is dependent on its terminal sedimentation velocity, as well as the upward velocity of the fluid. Where the terminal velocity exceeds the fluid velocity, the particle will settle against the current and report to the underflow and vice versa. This research will recreate the flow using computational fluid dynamics application to help us understand the variation of particle size or density of particles leading to different sedimentation velocities in the separation process.
Introduction
Plastic pellets, also introduced as nurdles, are the building blocks for almost every product made of plastic. About the size of a lentil, plastic pellets are produced by petrochemical chemical companies and transported to plastic manufacturing facilities where they are melted down and shaped into a final product. In 2015, it is estimated that 270 million metric tons of plastic are produced around the globe every year, much of which begins its life as a plastic pellet.
One typical problem along this industry is that producing plastic pellet always comes with some contaminants or dust which need to be removed. Those matters occur naturally in products like minerals, food, tablets, and other bulk solids, while others are caused by the way the products are handled. Impurities in plastic pellets, both fines (dust) and angel hair (streamers), are generated by the friction in conveying lines. Dilute phase systems create large amounts of dust and streamers; the higher the velocity, the larger the amounts of impurities.
For instance, as depicted in figure 1, these bends cause pellets to hit the inner wall of the elbow. Depending on the resin properties, elbow design, and air velocities, some resins get deflected to other areas of the elbow and some get deflected back to the air stream. Most slide against the elbow wall. This sliding generates frictional heat. pellets with low melting points, soften and smear along the wall. This smearing happens fast, and once started, it often grows as incoming pellets rub against the existing smear. Incoming conveyed pellets randomly break off the smeared plastic into long, ribbon-like strands, almost like loose bird’s nests which are called angel hair.
Cleaning bulk solids in the plastics industry is important to improve the quality of both the pellets and the finished plastic product. Dust and angel hair can contaminate resins at the receiver, including changing the resin’s properties and color. This problem also leads to lower quality end products such as weak spots in fibers, blurry surfaces resulting from vaporized dust particles, flaws in wire insulation, etc. the mixture of these impurities with unaffected resin often plugging a feed area and eventually starving a receiver. These clogged vent or duct resulting in shorter machine and equipment lifespan wherein increasing factory cost.
Therefore, separators based on a variation of density, size, and geometry are necessary to overcome the problem. Typical separator like screening isn’t appropriate for fines removal because the thread-like angel hair gets stuck in the mesh openings and gradually blinds the screen. While it is true that using airflow is very effective, the cyclonic separator is also unfavored since the movement along the cylindrical chamber would generate additional dust due to surface friction. This is why elutriator stands compared to the other method.
In a simple elutriator, as shown in Figure 2, the multiphase fluid flow will enter vertically into the elutriation chamber through the inlet located at the top of the elutriator. This flow will then be channeled to a diffuser at the center of the cylinder so that the fluid flow will form an annulus dome between the diffuser and the apparatus wall and the plastic pellet is evenly distributed. This distribution allows all pellets to be exposed to the wash air that blows upward and the elutriation will run optimally. In the elutriation zone, dust and contaminants that are relatively light will rise upwards and form an overflow. This overflow is discharged from the elutriator to a dust collector. Simultaneously, the plastic pellets will slowly fall down and form an underflow to the elutriator’s outlet, where a rotary airlock valve continuously discharges the pellets to the downstream process. In a pressure conveying system, the valve’s airlock function minimizes the leaking flow of wash air from the elutriator outlet, and in a vacuum conveying system, it minimizes airflow entering the elutriator.
Elutriation Principle
The interaction of particles moving through a fluid or in reverse is the basis of elutriation. Elutriation (the converse of sedimentation) is where a fluid (usually a gas) is forced through a powder bed, and can thus be used to determine particle size distributions. The elutriator utilizes a rising current of fluid to sweep the system free of particles smaller than a specific size. When the velocity of a rising current in a fluid system equals the terminal settling velocity of certain particle size, the particles remain stationary in the rising fluid. Larger particles have a greater terminal velocity and will settle toward the bottom. The size of a particle that remains suspended in a rising current of a given velocity will herein be referred to as the critical size. The settling velocity of particles in a rising current of fluid is governed by Stokes's Law. Therefore, A. Doroszkowski formulated the wash air velocity as follows:
Terminal-velocity constants for common shaped particles are
The particles can be fractionated according to size by varying the quantity of air passing through the air jets or by altering the size of the elutriation chamber. One can thus obtain a cumulative size distribution by collecting the various fractions in settling containers. Since different elutriators are difficult to govern generally, each plant must be analyzed particularly.
Objectives
Using computational fluid dynamics (CFD) application, the objectives of this study are as follows:
1. Performing CFD simulation of elutriation in selected geometry using various parameters from literatures
2. Investigating the relation between inlet velocity of wash fluid and the plastic pellet density in elutriation chamber.
3. Verifying the results through residual (or relative change) convergence test
4. Validating the results to existing study or literature.
Methodology
MP-PIC (Multi-phase Particle-in-cell)
Multiphase particle-in-cell (MP-PIC) is a mathematical model of separated particulate multiphase flow using a continuum for the fluid and a Lagrangian model for particles. This method allows an economical solution for flows with a wide range of particle types, sizes, shapes, and velocities. The MP-PIC method is described by the governing equations, interpolation operators, and the particle stress model.
- Fluid phase (continuum)
- The continuity equation for the fluid with no interphase mass transfer is
- where u f is the fluid velocity and θ f is the fluid volume fraction. The momentum equation for the fluid is
- where ρ f is the fluid density, p is fluid pressure, and g is the gravitational acceleration. F is the rate of momentum exchange per volume between the fluid and particle phases. The fluid phase is incompressible and fluid and particle phases are isothermal. The momentum equation presented here neglects viscous molecular diffusion in the fluid but retains the viscous drag between particles and fluid through the interphase drag force, F.
- Particle phase (lagragian)
- The dynamics of the particle phase is described using the particle probability distribution function φ (x, up, ρp, Ωp, t), where x is the particle position, up is the particle velocity, ρp is the particle density, and Äp is the particle volume. For the present, it is assumed that the mass of each particle is constant in time (no mass transfer between particles or to the fluid), but particles may have a range of sizes and densities. The particle φ change over time is obtained by solving a Liouville equation for the particle distribution function,
- where ∇u is the divergence operator with respect to velocity. where A is the particle acceleration discrete particle acceleration equals to
- The terms represent acceleration due to aerodynamic drag, pressure gradient, gravity, and gradient in the interparticle stress, τ.
- A numerical solution of the particle phase is obtained by dividing the distribution into a finite number of "computational particles" that each represents a number of real particles with identical mass density, volume, velocity, and location. At each time step, the velocity and location of each computational particle are updated using a discretized form of the above equations. The use of computational particles allows for a significant reduction in computational requirements with a negligible impact on accuracy under many conditions. The use of the computational particle in the Multiphase Particle-in-Cell method allows a full particle size distribution (PSD) to be modeled within the system as well as the modeling of polydisperse solids.
- Interpolation operators
- Particle properties are interpolated to and from the Eulerian grid in the MP-PIC scheme. Interpolation operator properties are defined which are both locally and globally conservative in mapping to and from the grid. Snider (2001) uses a staggered grid where momentum properties are calculated at cell faces and scalar properties are calculated at cell centers. Both scalar and momentum particle properties are needed. The continuity equation and pressure equation are calculated at cell centers. The momentum transfer between particles and gas is calculated at cell surfaces. This requires four sets of interpolation operators in three dimensions. Scalar properties, at cell centers, are mapped with one set of interpolation functions. Momentum properties, at face centers, are mapped with three other sets. The operators have the same definition but have different support in the axis of interpolation. Those transfer of particle properties is performed using linear interpolation functions.
- Particle stress model
- The particle normal stress is modeled by a continuum calculation of the particle pressure and the subsequent normal stress force is applied to discrete particles. The Lagrangian discrete particle stress model which uses the stress gradient, eliminates the need for an implicit solution for the particle normal stress (particle volume fraction). The model is robust and fast which makes it well suited for three-dimensional calculation. Collisions between particles, where particles are modeled as a continuum, are estimated by an isotropic interparticle stress where the off-diagonal elements of the stress tensor are neglected. Snider (2001) has suggested calculating the particle stress as τ;
- here θc is the close-pack volume fraction and β, Ps and ε are constants.
Simulation Properties
Geometry Model and Meshing
Boundary Condition
Computational Model and Simulation
Result and Analysis
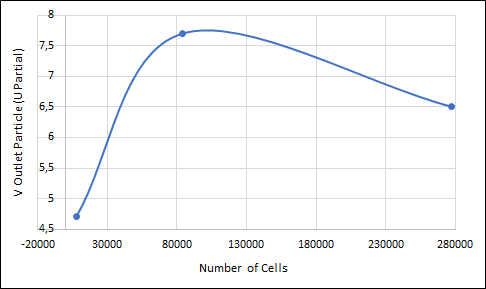
Mesh Independency Study
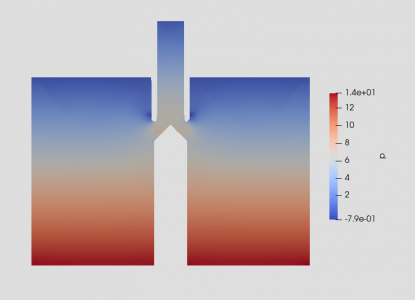
Mesh independency study is one criterion to assure the independence of solution from numerical error due to mesh resolution. Not checking this is a common cause of erroneous results in CFD, and this process should at least be carried out once for each type of problem that is analyzed. To perform the test, the value variable interest is monitored first in a small number of cells. Then, we can increase the number of mesh and recheck the interest value. This work must be undertaken until the interest value does not change with respect to the number of cells. In this observation, the value of variable interest is considered to be the pressure drop along the horizontal plane surrounding the diffuser. The result is given in the following figure
| Number of Cells | V Particle (Outlet) (m/s) |
|---|---|
| 7616 | 4,52 |
| 24861 | 6,1 |
| 84251 | 7,72 |
| 277504 | 6,5 |
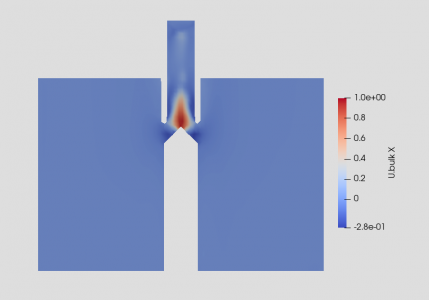
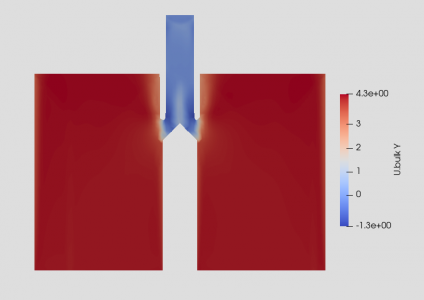
Distribution of U Bulk
Distribution of Pressure