Difference between revisions of "Tri Aji Setyawan"
(→MINGGU KE 3) |
(→MINGGU KE 3) |
||
| Line 46: | Line 46: | ||
| − | + | // Gauss-Jordan Algorithm | |
| + | // Transforms input matrix A into reduced row echelon form matrix B | ||
| + | // Christopher S.E. November 2020 | ||
| + | input Real [:,:] A; // An augmented matrix of m*n | ||
| + | output Real [:,:] B; // Output matrix in reduced row echelon form | ||
| + | // Local variables | ||
| − | + | protected | |
| + | Integer h = 1; // Initialize pivot row | ||
| + | Integer k = 1; // Initialize pivot column | ||
| + | Integer m = size(A,1); // Number of rows in matrix | ||
| + | Integer n = size(A,2); // Number of columns in matrix | ||
| + | Integer c = 0; // Index counter | ||
| + | Integer max_row; // Row index of max number in pivot column | ||
| − | + | Real [:] pivot_column; // Vector containing pivot column data | |
| − | + | Real [:] pivot_row; // Vector containing backwards pivot row data | |
| − | + | Real [:,:] temp_array; // Stores matrix data when switching rows | |
| − | + | Real r; // Ratio value used for row operations | |
| − | |||
| − | Real | ||
| − | Real | ||
| − | Real | ||
| − | Real | ||
| − | |||
| − | |||
| − | |||
| − | // | + | // Limit to handle floating point errors |
| − | + | Real float_error = 10e-10; | |
| − | |||
| − | + | algorithm | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | // Transfer input matrix A into variable B |
| − | + | B := A; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | while h <= m and k <= n loop |
| − | + | ||
| − | + | // Dealing with floating point errors | |
| − | + | for i in 1:m loop | |
| − | + | for j in 1:n loop | |
| − | + | if abs(B[i,j]) <= float_error then | |
| − | + | B[i,j] := 0; | |
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| − | // | + | // Finding the pivot |
| − | + | pivot_column := {B[i,h] for i in h:m}; | |
| − | + | ||
| − | + | // Get position index of lowest row with greatest pivot number | |
| − | + | c:= h-1; | |
| − | + | for element in pivot_column loop | |
| − | + | c := c+1; | |
| + | if abs(element) == max(abs(pivot_column)) then | ||
| + | max_row := c; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | // No pivot in this column, move on to next column | ||
| + | if B[max_row, k] == 0 then | ||
| + | k := k+1; | ||
| + | |||
| + | else | ||
| + | // Swap Rows h <-> max_row | ||
| + | temp_array := B; | ||
| + | temp_array[h] := B[max_row]; | ||
| + | temp_array[max_row] := B[h]; | ||
| + | B:= temp_array; | ||
| + | |||
| + | // Divide pivot row by pivot number | ||
| + | B[h] := B[h]/B[h,k]; | ||
| + | |||
| + | // For all rows below the pivot | ||
| + | for i in (h+1):m loop | ||
| + | |||
| + | // Store the ratio of the row to the pivot | ||
| + | r := B[i,k] / B[h,k]; | ||
| + | |||
| + | // Set lower part of pivot column to zero | ||
| + | B[i,k] := 0; | ||
| + | |||
| + | // Operations on the remaining row elements | ||
| + | for j in (k+1):n loop | ||
| + | B[i,j] := B[i,j] - B[h,j] * r; | ||
| + | end for; | ||
| + | |||
| + | end for; | ||
| + | |||
| + | // Move on to next pivot row and column | ||
| + | h := h+1; | ||
| + | k := k+1; | ||
| + | |||
| + | end if; | ||
| + | |||
| + | end while; | ||
| − | // | + | // The matrix is now in row echelon form |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | // | + | // Set values of (h,k) to (m,n) |
| − | + | h := m; | |
| − | + | k := n; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | while h >= 1 and k >=1 loop | |
| − | |||
| − | |||
| − | + | // Dealing with floating point errors | |
| + | for i in 1:m loop | ||
| + | for j in 1:n loop | ||
| + | if abs(B[i,j]) <= float_error then | ||
| + | B[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| − | // | + | // Finding the pivot |
| − | + | pivot_row := {B[h,i] for i in 1:k}; | |
| − | + | ||
| + | // Get position index k of pivot | ||
| + | c := 0; | ||
| + | for element in pivot_row loop | ||
| + | c := c+1; | ||
| + | if element <> 0 then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | k := c; | ||
| − | + | // No pivot in this row, move on to next row | |
| − | + | if B[h, k] == 0 then | |
| + | h := h-1; | ||
| + | |||
| + | else | ||
| + | |||
| + | // Perform row operations | ||
| + | for i in 1:(h-1) loop | ||
| + | r := B[i,k]; | ||
| + | B[i] := B[i] - B[h] * r; | ||
| + | end for; | ||
| + | |||
| + | // Move on to next pivot row and column | ||
| + | h := h-1; | ||
| + | k := k-1; | ||
| + | |||
| + | end if; | ||
| − | + | end while; | |
| − | |||
| − | + | // The matrix is now in reduced row echelon form | |
| − | |||
| − | + | end GaussJordan; | |
| − | |||
| − | + | === Tugas 3 Metode Numerik === | |
| − | + | Di akhir kelas, Pak Dai memberikan kami tugas yaitu menyelesaikan persoalan berikut: | |
| − | + | [[File:pr3-1.png|720px|center]] | |
| − | |||
| − | + | Berikut adalah penyelesaiannya: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <syntaxhighlight lang="modelica"> | |
| − | |||
| − | |||
| − | |||
| − | + | *class Trusses | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
parameter Integer N=8; //Global matrice = 2*points connected | parameter Integer N=8; //Global matrice = 2*points connected | ||
parameter Real A=0.001; //Area m2 | parameter Real A=0.001; //Area m2 | ||
| Line 282: | Line 301: | ||
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| − | end | + | end Trusses; |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 14:04, 2 December 2020
Biodata
Tri Aji Setyawan 1906301324
Saya merupakan mahasiswa teknik mesin UI angkatan 2019. saya menyukai teknik mesin karena tertarik pada bidang manufaktur dan karena teknik mesin sendiri memiliki prospek kerja yang luas. hal yang saya pelajari sebelum uts ini adalah mengenai turunan numerik, deret mclaurin , interpolasi, regresi, pengertian dari metode numerik, pseucode.
MINGGU KE 1
- Tujuan mempelajari metode numerik
- 1. matching dengan tujuan belajar: memahami konsep dan prinsip dasar di dalam metnum. contoh persamaan aljabar, algorithma, pencocokan kurva, persamaan diferensial parsial.
- 2. dapat menerapkan pemahaman terhadap konsep di dalam permodelan numerik ( pengaplikasian metode numerik )
- 3. mampu menerapkan metnum di dalam persoalan keteknikan.
- 4. untuk mencapai poin 1,2,3, yaitu dengan cara moral value (adab). untuk menambah nilai tambah / adabsehingga kita menjadi orang yang lebih beradab
TUGAS 1
Pada pertemuan sebelumnya , saya mendapatkan tugas untuk membuat video terkait penggunaan aplikasi open modelica
MINGGU KE 2
perbedaan openmodelica dengan python , open modelicca lebih ke bahasa permodelan sedangkan python hanya bahasa cpoding. kelebihan dari open modelicca yaitu :
- menggunakan bahasa permodelan yang cocok untuk seorang engineer
- proses perhitungan lebih cepat
- pengguna aplikasi openmodelica cukup banyak penggunanya, dan termasuk open teknologi (free).
pada minggu kedua, saya mempelajari mengenai cara memanggil fungsi dalam suatu kelas tertentu
Tugas 2
mengaplikasikan penggunaan fitur function dan class pada open modelica. Membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut. Persamaan aljabar simultan adalah sebuah persoalan matematika yang kompleks sehingga penyelesaian perlu dengan menggunakan tools, agar dapat dibuat lebih sederhana.
pada tugas kali ini saya mencoba menyelesaikan suatu soal sistem persamaan linier menggunakan metode gauss
MINGGU KE 3
// Gauss-Jordan Algorithm // Transforms input matrix A into reduced row echelon form matrix B // Christopher S.E. November 2020 input Real [:,:] A; // An augmented matrix of m*n output Real [:,:] B; // Output matrix in reduced row echelon form // Local variables
protected Integer h = 1; // Initialize pivot row Integer k = 1; // Initialize pivot column Integer m = size(A,1); // Number of rows in matrix Integer n = size(A,2); // Number of columns in matrix Integer c = 0; // Index counter Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column; // Vector containing pivot column data Real [:] pivot_row; // Vector containing backwards pivot row data Real [:,:] temp_array; // Stores matrix data when switching rows Real r; // Ratio value used for row operations
// Limit to handle floating point errors Real float_error = 10e-10;
algorithm
// Transfer input matrix A into variable B B := A;
while h <= m and k <= n loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_column := {B[i,h] for i in h:m};
// Get position index of lowest row with greatest pivot number
c:= h-1;
for element in pivot_column loop
c := c+1;
if abs(element) == max(abs(pivot_column)) then
max_row := c;
end if;
end for;
// No pivot in this column, move on to next column
if B[max_row, k] == 0 then
k := k+1;
else
// Swap Rows h <-> max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
// Divide pivot row by pivot number
B[h] := B[h]/B[h,k];
// For all rows below the pivot
for i in (h+1):m loop
// Store the ratio of the row to the pivot
r := B[i,k] / B[h,k];
// Set lower part of pivot column to zero
B[i,k] := 0;
// Operations on the remaining row elements
for j in (k+1):n loop
B[i,j] := B[i,j] - B[h,j] * r;
end for;
end for;
// Move on to next pivot row and column
h := h+1;
k := k+1;
end if;
end while;
// The matrix is now in row echelon form
// Set values of (h,k) to (m,n) h := m; k := n;
while h >= 1 and k >=1 loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_row := {B[h,i] for i in 1:k};
// Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k := c;
// No pivot in this row, move on to next row
if B[h, k] == 0 then
h := h-1;
else
// Perform row operations
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] * r;
end for;
// Move on to next pivot row and column
h := h-1;
k := k-1;
end if;
end while;
// The matrix is now in reduced row echelon form
end GaussJordan;
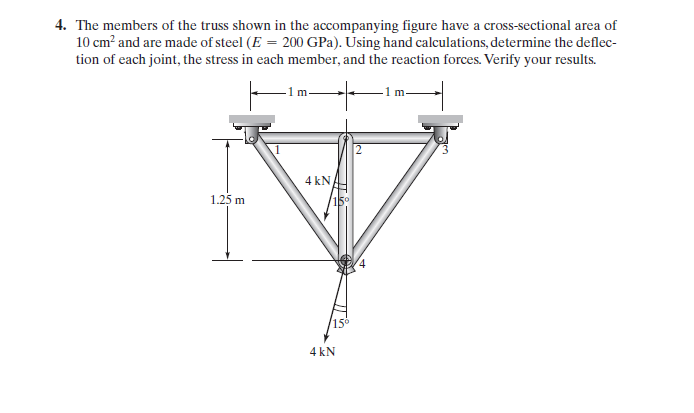
Tugas 3 Metode Numerik
Di akhir kelas, Pak Dai memberikan kami tugas yaitu menyelesaikan persoalan berikut:
Berikut adalah penyelesaiannya:
<syntaxhighlight lang="modelica">
- class Trusses
parameter Integer N=8; //Global matrice = 2*points connected parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1];
//boundary condition Integer b1=1; Integer b2=3;
//truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N];
//truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N];
//truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N];
//truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N];
//truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N];
/* for each truss, please ensure pXa is lower then pXb (X represents truss element number)
- /
algorithm
//creating global matrice K1:=Stiffness_Matrices(X1); G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2); G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3); G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4); G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5); G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5; Ginitial:=G;
//implementing boundary condition for i in 1:N loop
G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1;
//solving displacement Sol:=Gauss_Jordan(N,G,X);
//solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;