Difference between revisions of "Analisis pondasi rumah panggung oleh Ruhama Sidqy"
Ruhamasidqy (talk | contribs) (Created page with "PR 2 KOMPUTASI TEKNIK: ANALISIS PONDASI RUMAH PANGGUNG '''Tugas''': Analisis hubungan tegangan dan regangan dari sebuah pondasi yang dikenai gaya aksial ke bawah sebesar F =...") |
Ruhamasidqy (talk | contribs) |
||
| Line 1: | Line 1: | ||
PR 2 KOMPUTASI TEKNIK: ANALISIS PONDASI RUMAH PANGGUNG | PR 2 KOMPUTASI TEKNIK: ANALISIS PONDASI RUMAH PANGGUNG | ||
| + | |||
| + | Oleh: Ruhama Sidqy - 1806244553 | ||
'''Tugas''': Analisis hubungan tegangan dan regangan dari sebuah pondasi yang dikenai gaya aksial ke bawah sebesar F = 100 N seperti ditunjukkan pada gambar. | '''Tugas''': Analisis hubungan tegangan dan regangan dari sebuah pondasi yang dikenai gaya aksial ke bawah sebesar F = 100 N seperti ditunjukkan pada gambar. | ||
Latest revision as of 07:25, 17 February 2019
PR 2 KOMPUTASI TEKNIK: ANALISIS PONDASI RUMAH PANGGUNG
Oleh: Ruhama Sidqy - 1806244553
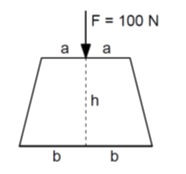
Tugas: Analisis hubungan tegangan dan regangan dari sebuah pondasi yang dikenai gaya aksial ke bawah sebesar F = 100 N seperti ditunjukkan pada gambar.
Asumsi: Pondasi berbentuk seperti potongan kerucut dengan jari-jari tutup adalah a dan jari-jari alas adalah b, serta tinggi h. Abaikan pengaruh gaya berat terhadap regangan yang dialami pondasi.
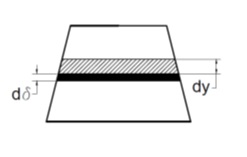
Solusi: Karena luas permukaan melintang pondasi tidak sama dan bergantung pada y maka kita ambil irisan dari pondasi dengan ketebalan dy. Irisan tersebut kemudian kita tinjau dan integralkan untuk mendapatkan deformasi total. Nilai y diukur dari atas ke bawah.
Pada pondasi bekerja suatu gaya aksial sehingga pondasi tersebut mengalami tegangan tekan yang besarnya didapatkan dari persamaan
σ=F/A=F/(πr^2 )
di mana A dan r masing-masing adalah luas dan jari-jari dari permukaan melintang. Nilai r adalah fungsi dari y yaitu
r=a+(b-a)/h y
Akibat tegangan normal, pondasi mengalami deformasi sebesar dδ dan menghasilkan regangan sebesar
ϵ=dδ/dy
Dari hukum Hooke diketahui bahwa tegangan berbanding lurus terhadap regangan dengan konstanta perbandingan yang disebut sebagai modulus elastisitas atau modulus Young, persamaan ini dapat dituliskan sebagai σ=Eϵ.
Dengan menggabungkan persamaan-persamaan di atas maka kita akan mendapatkan
F/(πr^2 )=dδ/dy
Dengan mensubtitusi nilai r kemudian mengintegralkan persamaan di atas – pengintegralan dapat dilakukan secara manual atau menggunakan software seperti EES atau MATLAB – maka akan kita dapatkan persamaan berikut
δ=Fh/πEab
Persamaan di atas menunjukkan deformasi total yang dialami oleh pondasi