Tugas Pertemuan 1 (Rizki Aldila Umas)
Pertanyaan: Selesaikan persaman matematika berikut ini, dengan menggunakan pendekatan metode numerik!
Berapakah f(x) saat x = 1?
Jawab:
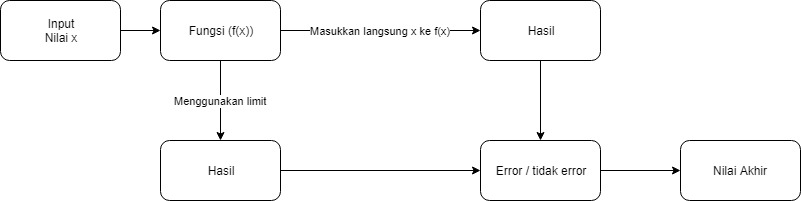
Flowchart penyelesaian masalah matematis:
Sebelum berlanjut, disini saya menggunakan JupyterLab yang berada di dalam Anaconda Navigator. Graphical User Interface (GUI) ini dapat membantu dalam pembelajaran ini, terutama saat mempelajari bahasa pemrograman Python.
Memasukkan nilai x langsung ke dalam fungsi
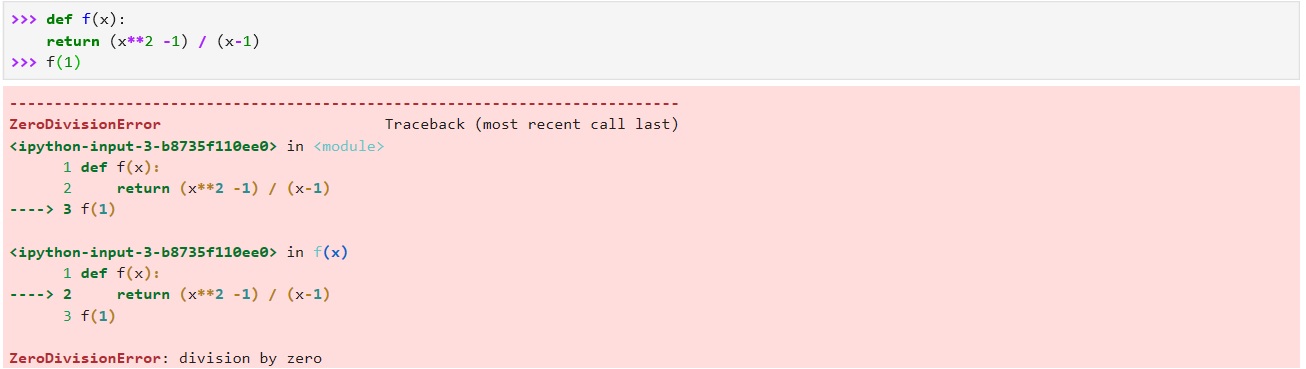
Dalam melakukan penghitungan untuk suatu fungsi seperti ini, terlebih dahulu kita coba mendefinisikan langsung fungsinya dan kemudian memasukkan nilai x yang tertera yakni dalam hal ini adalah x=1. Hal ini ditujukan untuk mengecek apa yang akan terjadi pada penghitungan tersebut, jika mendapatkan suatu nilai yang langsung / tetap maka jawaban tersebut dapat diterima.
Dan dapat dilihat, ternyata terjadi error yaitu karena pembagian oleh 0 yang akan dibahas pada bagian selanjutnya.
0/0
Error yang terjadi adalah 0/0 tidak terdefinisi. Para matematikawan sepakat bahwa semua angka dibagi dengan 0 akan menghasilkan suatu nilai tidak terdefinisi, oleh karenanya mari kita berpikir dengan logika matematika seperti filosofi matematika yang ada di halaman pertama profil ini. Untuk mencari nilai 0/0 diperlukan beberapa argumen, dan dalam kasus ini saya ingin mencoba membahasnya 1 per 1. Berikut ini penjelasannya:
Untuk mendekati nilai 0/0 maka ada 2 cara yang dapat dinggap valid dan keduanya menggunakan argumen yang sama, bahwa tidak ada angka yang 100% eksak seperti yang dituliskan pada profil awal. Cara yang pertama adalah sebagai berikut:
Untuk mendekati nilai 0/0, maka kita dapat menggunakan angka yang sangat kecil sehingga mendekati 0/0 contohnya dengan 0,0000001/0,000001 yang hasilnya adalah 1. Mungkin kita akan membuatnya lebih kecil lagi, misalkan 0,0000000001/0,0000000001 yang hasilnya akan tetap sama yaitu 1. Oleh karenanya, dengan argumen berikut diterima hasil dari 0/0 =1 dapat diterima.
Namun tidak berhenti sampai disitu saja, ada cara kedua dalam menyelesaikan masalah ini yaitu:
Untuk mendekati nilai 0/0, maka dapat dengan cara 0 dibagi dengan angka yang sangat kecil sehingga mendekati 0/0, contohnya adalah dengan 0/0,00001 yang hasilnya adalah 0. Atau mungkin membuat pembaginya lebih kecil lagi, misalkan dengan 0/0,0000000001 dan hasilnya akan tetap sama yaitu 0. Dengan diterimanya argumen ini maka hasil 0/0 = 1 dapat diterima
Oleh karenanya, ketika kita menggunakan argumen pertama, maka argumen kedua harus ditolak, dan begitu juga sebaliknya padahal pendekatannya relatif sama. Oleh karena itu 0/0 disepakati menghasilkan suatu bilangan yang tidak terdefinisikan .
Menggunakan limit mendekati 1
Operasi limit digunakan karena nilai 0/0 yang tidak terdefinisi jika x langsung dimasukkan saja. Operasi limit ini dalam suatu sistem pemrograman python harus didefinisikan terlebih dahulu sebelum dapat dimulai perhitungannya. Karena pada dasarnya python hanya dapat melakukan operasi perhitungan matematis +;-;x;:; (tambah, kurang, kali, dan bagi) saja. Karena pengetahuan saya yang terbatas hanya pada pendefinisian fungsi, tanpa tau bagaimana cara membuat loop agar dapat mendefinisikan limit. Maka saya mengerjakan tugas ini dengan cara merubah input (x) sehingga mendekati x=1 seperti cara berikut ini.
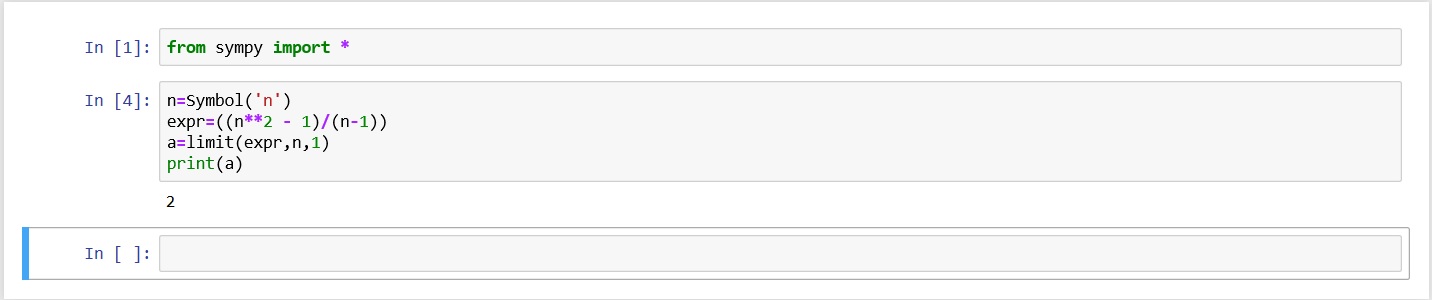
Terdapat cara lain untuk melakukan pendefinisian yang dapat dimengerti oleh python yaitu dengan menggunakan syntax yang sudah ditulis oleh orang lain dalam SymPy ,yang di webnya mendefinisikan mereka sendiri sebagai "perpustakaan dari simbol dan operasi matematis untuk python". Mereka telah mendefinsikan limit, sehingga dapat digunakan oleh kepentingan umum. Dengan menggunakan syntax yang di import dari Sympy maka hasilnya adalah sebagai berikut: