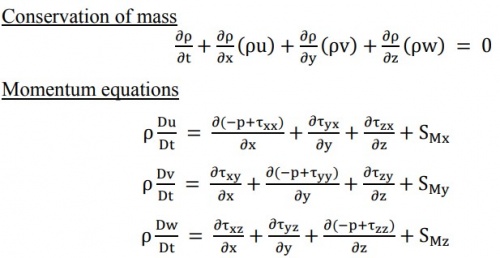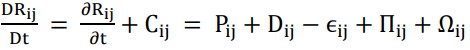Difference between revisions of "TUGAS BESAR APLIKASI CFD: '''Two-Phase Simulation in Horizontal Flow Gas-Liquid Separator'''"
Alesdaniel (talk | contribs) (→Conclusions) |
Alesdaniel (talk | contribs) (→Acknowledgement) |
||
| Line 155: | Line 155: | ||
== Acknowledgement == | == Acknowledgement == | ||
| − | This | + | This work was carried out as a final assignment in the Computational Fluid Dynamics course at the Department of Mechanical Engineering, University of Indonesia. The author gratefully acknowledges the help provided by Dr. Ir. Ahmad Indra Siswantara, as this paper's advisor. The author also thanks M Hilman Gumilar Syafei, Abdullah Robanni, Bintang Farhan, Abi Rizky, Elvin, Agus P Nuryadi, Josiah Enrico, and the rest of my colleagues who took this course. |
== References == | == References == | ||
Revision as of 19:29, 5 January 2021
Contents
Abstract
Introduction
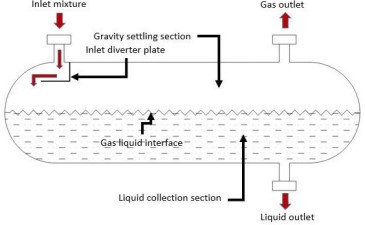
Petroleum reaches the surface as a mixture consisting of gas and fluid substance. To achieve an adequate quality of petroleum, one needs to satisfy a petroleum refinery process, which requires deliberation in multiphase separation. A gas-liquid separator was designed to separate two different substances using a diverter inside the system. To acquire efficient separation, one needs to consider the effective diverter near the system's inlet. This consideration requires a perilous investigation, which numerical modeling would be utilized in achieving the low cost and minimum risk investigation upon the system. In petroleum production, there are several types of separators. The separators are used based on the numbers of phases, crude oil properties, and separator conditions. These are vertical, horizontal, and spherical separators, which are widely used in production. Regarding the lowes cost expense in these separators, the horizontal separator has the lowest ones. This separator is considered as a gravity-based facility that was designed to provide sufficient time for droplets separation. The schematic flow direction of this system will be depicted below to ensure the simplicity of the system.
Objectives
In this simulation, there will be various assumptions due to the model limitations. First of all, the model that will be simulated applies for a two-phase separator only. The real case in using the system would be in a three-phase consideration. Second, there would be numerous neglections since the simulation only focuses on the two-phase separation. There would be no other additional phase separators, such as coalescer, vortex breaker, or baffle, widely used in the actual system. The simulation will only focus on the inlet velocity and separator distance variation to acquire its effectiveness. For further objectives will be mentioned below:
1. To evaluate the system's effectiveness by comparing the previous simulation with the redesigned 3D simulation.
2. To investigate the most efficient separator within several distances from the inlet and various inlet velocities.
3. To investigate the suitable separator with and without a perforated separator.
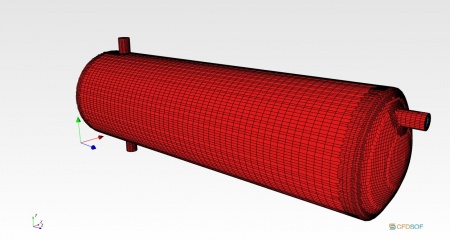
Numerical Geometry
The geometry would be the same as the previous study by Efendioglu, et al. (2014), and the regulations on oil handling systems. For simplicity in simulation, the geometry would be in two-dimension, and the result's validation will be performed to achieve the similarities from the 3D simulation. The additional internal apparatuses would be neglected and only using the diverter considered in the simulation. This would point out each of the phase separations as perceptible as the post-processor can with acceptable information to a certain condition. In this simulation, the diverter's distance bears a close resemblance to the one proposed by Bayraktar, et al. (2017), with customization of limiting the diverter distance up to 180 mm from the inlet. The distances are an interval of 20 mm from 100 mm until 140 mm, and an additional 180 mm distance. It was decided that the best method for this study was to evaluate the actual approach in obtaining the flow rate at the system's outlet.
The diverter would then be modified into a perforated baffle applied in an actual horizontal separator. In this case, the procedure used is as proposed by Efendioglu et al. (2014) and Wilkinson et al. (2000) [5]. The perforated baffle diameter is 12 mm and 25 mm (Figure 4. and Figure 5.), and each of them is compared with the unperforated baffle (Figure 3.). This then will also be compared between the flow rate at the system's outlet. The scope of this study is to obtain evidence that using a perforated separator would increase the efficiency in delivering the oil into the outlet.
Methodology
Software
The numerical simulation will be using CFDSOF® (for the pre-processing and the processing step), the first Indonesian CFD software established by PT CCIT Group Indonesia, and ParaView as the post-processor of the simulation.
Mathematical Model (Verification)
The simulation was solved using the Large Eddy Simulation (LES), k-ε turbulence model. In order to ease the visualization between phases, the multiphase Eulerian-Langrangian model is being implemented, which attributes separate momentum and continuity equations for each phase. The flow is assumed to be incompressible, which then the governing equation in this simulation can be written as below:
These equations represent the simulation between the phases, which in this case is between oil droplets and gas. Because the flow incompressibility occurs during the numerical simulation, the energy equation is neglected. The turbulence equation for the gas phase has been widely addressed by previous researchers using the Reynolds stress equation[6]. It can be written as:
Cij represents the rate of convection, Pij is the production rate, Dij is the transport by diffusion, ϵij is the rate of dissipation, Πij is the transport due to turbulent pressure strain interactions Ωij is the transport due to rotation.
In this study, the oil is considered as droplets with a certain diameter. In this case, the droplets are assumed to be 10 μm. The drag that occurred upon droplets is presumably in the sphere-drag model, injected through the system's inlet. In this simulation, there is no evidence regarding the parcel numbers that occur in the system from the previous studies. However, the simulation setup bears a close resemblance to the same as the one proposed by Efendioglu, et al. [6] and Yayla, et al. [1]. The simulation is assumed to use the mass flow rate from both pieces of literature in order to reach the similarity in numerical simulation. Such an unjustified assumption can lead to grave consequences with regard to the result of the simulation. It is satisfied by the two-dimensional numerical simulation result.
Grid Independent Study
A grid independent study was performed to achieve minimum error in the simulation. The geometry without separator was used in this study to achieve the result. Mesh changes in each of the coordinates were compared with the velocity at the outlet. The study was started from the coarse grid until the fine grid to point out some differences. However, this study has a limitation when applying the solved geometry in the Paraview post-processor. A satisfactory justification regarding the mesh is varying the mesh in low numbers. This achieves an acceptable result by comparing velocities in each of the simulation outlets. In this grid independent study, the mesh that has been used for further simulations are 75x75x60 divisions. A division that exceeds the current division resulted in an error in post-processing visualization. The data that has been measured is explained in detail division measures below:
| Mesh Division | Velocity (m/s) |
|---|---|
| 10 x 10 x 10 | 2,04 |
| 30 x 30 x 30 | 2,7 |
| 45 x 45 x 45 | 4,08 |
| 60 x 60 x 60 | 4,8 |
| 75 x 75 x 60 | 5,32 |
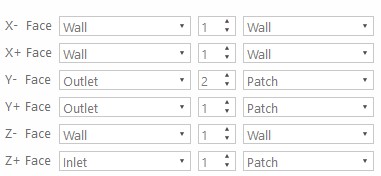
Boundary Conditions and Solver Control
The boundary conditions are assumed to be one inlet and two outlets. Both of the outlets use a different amount of pressure due to the height effect. The bottom outlet is 14.58 Pa, and the upper outlet is 0 Pa. This assumption is based on the basic hydrostatic pressure formula. Although the previous studies have shown that the inlet flow was set to be a certain mass flow rate, this simulation uses a certain amount of velocity regarding the software's limitations. In this simulation, the velocity inlet was assumed to be 5 m/s for both oil droplets and airflow through the inlet. Given that these findings are based on a limited flow rate available from the software, the results from such analyses should thus be treated with many assumptions. The height uses the bottom outlet as the datum, and gas density is used. The fluid properties on both phases and boundary conditions are written specifically in the table below:
| Fluid Type | Density (kg/m3) | Dynamic Viscosity (Pa.s) | Mass Flow Rate (kg/s) |
|---|---|---|---|
| Oil | 824.95 | 0.00237 | 0.5 |
| Gas | 1.225 | 1.79E-5 | 0.5 |
Results and Discussions
Validation
The simulation was first investigated under two-dimensional numerical simulation, using the same geometry. The two-dimensional simulation opted for simplification regarding the simulation. A single-phase simulation was examined in the simulation to achieve a simplification of the validity of the results. This was done utilizing CFDSof software with Paraview as the post-processor. However, it was found that the simulation does not satisfy the governing equation. These findings are in contradiction to previous results reported in the literature. It somehow differs from the basic equation of hydrostatic pressure in visualizing the system's pressure and velocity. The study was unsuccessful in proving that two-dimensional numerical simulation would satisfy a justification for the three-dimensional approach. Despite the unsatisfactory results, the next simulation is using a three-dimensional and multiphase approach. The simulation is still restricted only using two-phase, which are gas and oil droplets. It is plausible that a number of limitations could have influenced the results obtained.
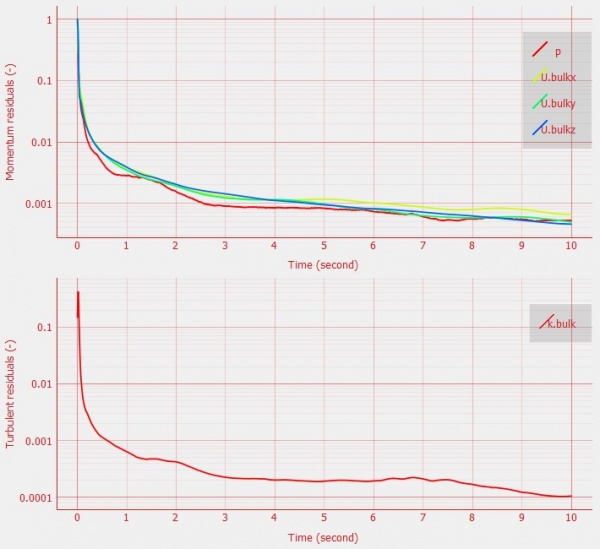
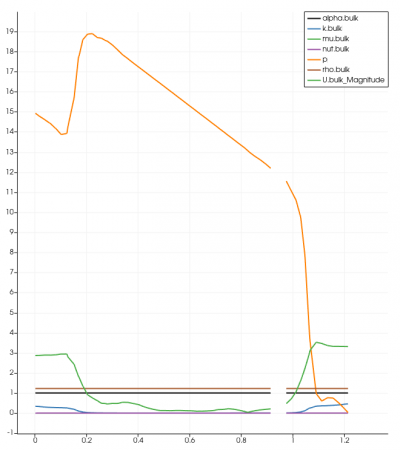
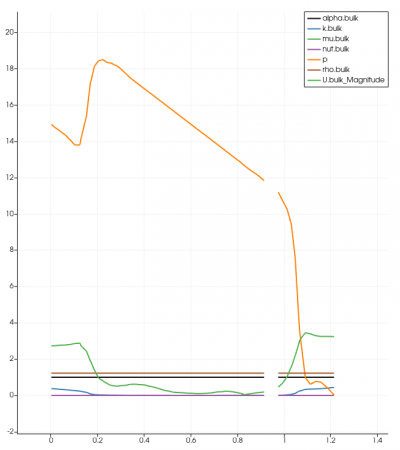
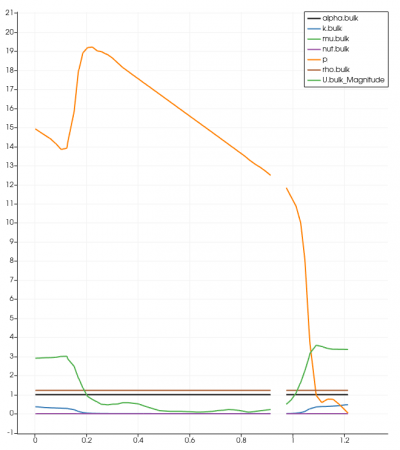
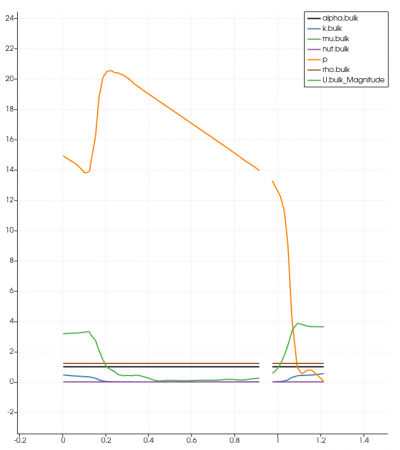
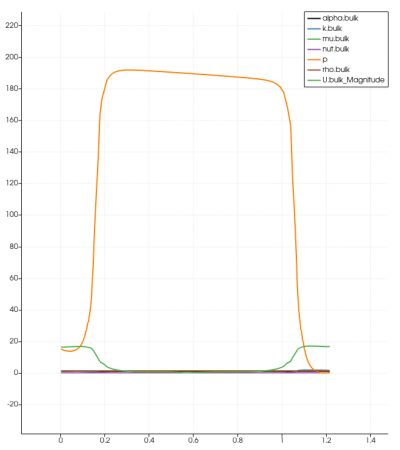
The simulation was done in transient-state with the LES Turbulence model. It was solved in 10 seconds time control with 0.01 seconds time step. The expected residual in this simulation was 10-6 for every iteration performed. Unfortunately, the results did not achieve the targeted amount after 10 seconds of iteration. This could lead to insufficiency in terms of providing accurate data and visualization. However, the residual was acceptable although it did not meet the required amount. It reached under 10-4, which in this case is acceptable. The graph for every simulation was similar to another, and below is one of the residual graphs:
Results
Separator Distance Variations
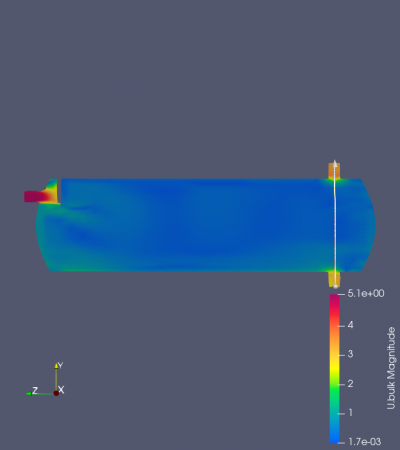
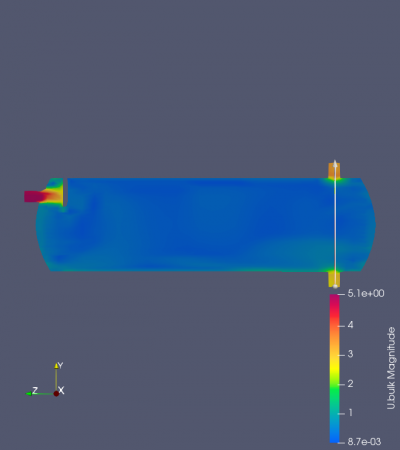
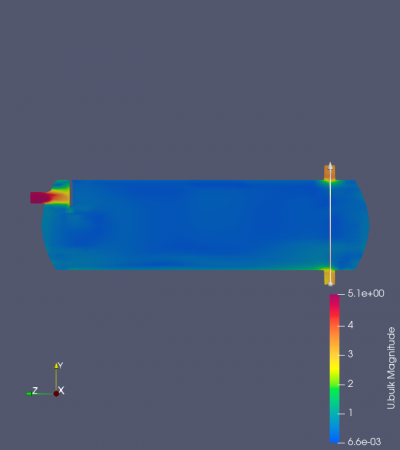
Surprisingly, with an assumed value of velocity inlet around 5 m/s, magnitudes of the system were found in different separator distances. As might have been expected, every result was not successful in proving similarities with the previous research. It was found that using the variety of separator distances and the magnitude did not indicate oil droplets and gas migration into the system's outlet (Figure). Despite the lack of visualization, the findings are compared with the previous results regarding the system's outlet in various separator distances. Figure _ until _ depicts that the system's velocity outlet in the Y-axis increases in separator distance increment. These results have shown a similarity between the present study with the previous study by Bayraktar, et al. (2017) and Efendioglu et al. (2014). Although the performance was not ideal, this simulation is still believed that there is a satisfactory agreement in both the system's outlets.
Regarding the system's efficiency, there were some discrepancies due to the software's limitation in boundary conditions, as expected beforehand. The efficiency is calculated from the bottom outlet's mass flow rate to the inlet's mass flow rate. The mass flow rate for the system's inlet was assumed to be 0.5 kg/s, according to the previous study by Bayraktar, et al. (2017). In this case, due to the software's limitation, oil droplets were assumed to be in a discrete phase, which was also considered as a particle. This led to a discrepancy in achieving the viscous effect that occurs during the simulation. A manual investigation by integrating the surface vector using the integrate variable feature in the ParaView software was also done to find the flow rate. It still did not fulfill the requirement to achieve the system's efficiency due to the velocity outlet that is greater than the inlet. Another alternative was then found by using lower mesh divisions because the higher mesh indicated a piece of information that stated Failed 1 mesh checks. It was then finally managed through another investigation and resulted in significant differences.
An alternative version was done to prove the previous study. It also managed to calculate the system's efficiency, although the calculation was not performed through mass flow rate. The mass flow rate calculation was unable to be performed due to the limitations in ParaView software. The efficiency was obtained through the surface integral of the outlet's area to the inlet's area. It was then calculated based on the flow rate that occurs in the system. This is slightly different from the previous attempt through mass flow rate calculation. Despite the different methods, the current calculation is acceptable regarding the velocity should meet the indication of the flow that travels in the system. Based on the result, the more distance between the inlet and the separator should increase the number of efficiencies, which in this case, the 180 mm distance reaches 60.3%. This is slightly different from the previous attempt by Bayraktar, et al. (2017) and Efendioglu et al. (2014), which shows a large percentage of efficiency around more than 90%. Despite that, this simulation succeeds in fulfilling the requirement in achieving the systems that should have done. The evidence from this study implies that a much farther distance of the separator would increase the system's efficiency.
| Mesh Division | Distance from Inlet Velocity (m) |
|---|---|
| 100 mm | 53.1% |
| 120 mm | 51.5% |
| 140 mm | 54.5% |
| 180 mm | 60.3% |
Perforated Separator
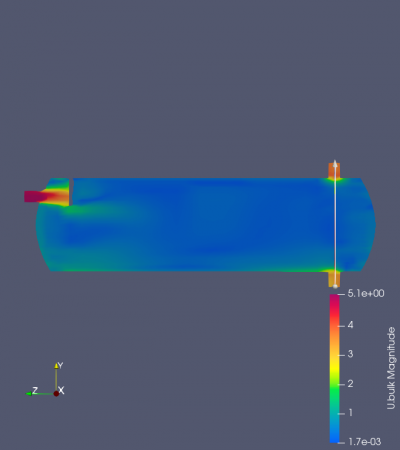
In this section, the same simulation was performed as the previous one. The differences here were perforated separators by previous studies from Wilkinson et al. (2000). These simulations then compared with the previous result with the one unperforated separator. This comparison is fixed in one distance between the inlet and the separator, at 100 mm. Based on the visualized velocity magnitude, the perforated result achieved a greater velocity than the previous one (Figure _.). Based on the visualization by ParaView software, it shows that the flow penetrates through the hole of the perforated separator. This then embarked on the perforated separator's advantage in providing a sufficient mass flow rate. However, this result still brought a discrepancy in the expected result. It achieved a greater outlet velocity (Graph _.), but still far as expectation regarding the flow separated by the separator should have been lowered when travels into the system's outlet. In the actual previous study, the perforated separator should have increased the system's efficiency due to the filtered oil droplets that occurred. Although the current result slightly misses proofing the past evidence, it still shows that the separator increases the system's efficiency in delivering oil droplets into the system's outlet. The result of this study suggests that an additional perforated separator increases the flow rate of the oil droplets that travel inside the system.
The other perforated separator, which is 25 mm in diameter, should be analyzed regarding the results. The current 12 mm in diameter perforated separator should also be analyzed using the previous section simulation with 30x30x30 division to achieve a successful mesh generation. However, there was a problem that unable to perform such kind of simulation. The meshed separator was generated in unperforated conditions for the 12 mm in diameter and the other disappears after the mesh has been generated. Although such limitations occurred during the simulation and not able to obtain the same result from the previous studies, it was still acceptable from the current result that it satisfies the calculation.
Conclusions
In summary, the work of two-phase numerical simulation in horizontal flow gas-liquid separator could gain a beneficial impact in processing crude oil. Although some evidence from the simulation implies that the current effectiveness is lower than the previous study, it still provides acceptable results. The separator will suffice the separation if the distance is large enough to achieve a greater outlet flow rate. The additional perforated separator also increases the effectiveness of the system in separating the oil and the gas. The work clearly has some limitations. Nevertheless, this work could be a framework for future numerical simulation. It is recommended that further research should be undertaken with accurate meshing and actual data of both phases. This numerical simulation and development in horizontal separators will be a challenge for us for next years.
Acknowledgement
This work was carried out as a final assignment in the Computational Fluid Dynamics course at the Department of Mechanical Engineering, University of Indonesia. The author gratefully acknowledges the help provided by Dr. Ir. Ahmad Indra Siswantara, as this paper's advisor. The author also thanks M Hilman Gumilar Syafei, Abdullah Robanni, Bintang Farhan, Abi Rizky, Elvin, Agus P Nuryadi, Josiah Enrico, and the rest of my colleagues who took this course.
References
[1] Yayla, Sedat & Kamal, Karwan & Bayraktar, Seyfettin & Oruç, Mehmet. (2017). TWO PHASE FLOW SEPARATION IN A HORIZONTAL SEPARATOR BY INLET DIVERTER PLATE IN OILFIELD INDUSTRIES.
[2] Eissa, M., 2013. Influence of Flow Characteristics on the Design of Two-Phase Horizontal Separators. Journal of Engineering and Computer Science (JECS), 15(2), pp.50-62.
[3] Adeniyi, O., 2004. Development of Model and Simulation of a Two-Phase, Gas-Liquid Horizontal Separator. Leonardo Journal of Sciences, 3(5), pp.34-45.
[4] Kharoua, N., Khezzar, L. and Saadawi, H., 2013. CFD modelling of a horizontal three-phase separator: a population balance approach. American Journal of Fluid Dynamics, 3(4), pp.101-118.
[5] Wilkinson, D., Waldie, B., Nor, M.M. and Lee, H.Y., 2000. Baffle plate configurations to enhance separation in horizontal primary separators. Chemical Engineering Journal, 77(3), pp.221-226.
[6] Efendioglu, A., Mendez, J. and Turkoglu, H., 2014. The numerical analysis of the flow and separation efficiency of a two-phase horizontal oil-gas separator with an inlet diverter and perforated plates. Advances in Fluid Mechanics, 10, p.133.
[7] Stewart, M. and Arnold, K.E., 2011. Surface production operations, Volume 1: Design of oil handling systems and facilities (Vol. 1). Elsevier.