Metode Simpson untuk Integrasi Numerik

1. Latar Belakang

Seiring pesatnya perkembangan teknologi dan kemajuan zaman, maka diperlukan suatu produk dengan ketelitian dan akurasi tinggi, dan waktu pengerjaan yang singkat. Begitu juga dengan permasalahan dalam bidang ilmu pengetahuan fisika murni maupun terapan, bidang rekayasa teknik metalurgi, mesin, elektro, sipil dan lain-lain dituntut hal yang sama, dimana dalam suatu perhitungan dengan data numerik membutuhkan ketelitian dan akurasi yang cukup baik. Pada saat teknologi informasi belum ada atau boleh dikatakan belum maju pesat, para praktisi dan profesional di bidang rekayasa teknik dan sain menganalisa dengan perhitungan manual. Simplifikasi digunakan dimana struktur yang sangat kompleks disederhanakan menjadi struktur yang lebih sederhana. Artinya akan terjadi perbedaan dari suatu permodelan dengan kondisi aktual. Hal ini dilakukan untuk menghindari kesulitan dalam analisa.

Adanya perkembangan teknologi informasi yang sangat pesat pada saat ini mendorong para praktisi untuk mengembangkan cara baru agar pekerjaan analisa dapat dilakukan dengan lebih baik dan lebih efektif. Metode kalkulasi dengan matriks dapat dilakukan dengan mudah menggunakan teknologi informasi. Sudah banyak persoalan di bidang teknik maupun sain yang dapat diselesaikan dengan menggunakan permodelan matematika. Sering kali permodelan matematika tersebut muncul dalam bentuk yang tidak ideal, sehingga tidak dapat diselesaikan dengan menggunakan metode analitik untuk mendapatkan solusi sejatinya (exact solution).

Jika persoalan-persoalan yang kita hadapi tidak dapat diselesaikan dengan metode permodelan matematika metode analitik menggunakan dalil-dalil kalkulus, maka solusinya dapat diperoleh dengan metode numerik. Metode numerik secara harfiah berarti suatu cara berhitung dengan menggunakan angka-angka, sedangkan secara istilah metode numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat diselesaikan dengan operasi aritmatika biasa.

Dengan menggunakan metode numerik, solusi exact dari persoalan yang dihadapi tidak akan diperoleh. Metode numerik hanya bisa memberikan solusi yang mendekati atau menghampiri solusi sejati sehingga solusi numerik dinamakan juga solusi hampiran ( approximation solution). Pendekatan solusi ini tentu saja tidak tepat sama dengan solusi sejati, sehingga ada selisih antara keduanya. Solusi tersebut disebut solusi galat (error). Semakin kecil galat yang diperoleh berarti semakin dekat solusi hampiran yang diperoleh dengan solusi sejatinya.

Berikut ini adalah beberapa metode integrasi numerik yang popular digunakan:

a. Trapezoidal Rule (Aturan Trapesium)

b. Simpson’s 1/3 Rule

c. Multiple -application Simpson’s 1/3 Rule

d. Simpson’s 3/8 Rule.

e. Newton Cotes.

f. Romberg Integration.

g. Gauss Quadrature.

Pada bahasan ini akan difokuskan pada integrasi numerik dengan menggunakan metode integrasi Simpson.

2. Metode Integrasi Simpson

Metode ini berasal dari matematikawan Thomas Simpson (1710–1761), yang berasal dari Leicestershire, Inggris. Kaidah Simpson banyak digunakan, misalnya oleh arsitektur perkapalan untuk menghitung kapasitas kapal atau sekoci.

Metode integrasi Simpson menggunakan polinomial order lebih tinggi (dibanding metode Trapesium) untuk menghubungkan titik-titik data. Misalnya, apabila terdapat satu titik tambahan di antara f (a) dan f (b), maka ketiga titik dapat dihubungkan dengan fungsi parabola (Gambar 1a). Apabila terdapat dua titik tambahan dengan jarak yang sama antara f (a) dan f (b), maka keempat titik tersebut dapat dihubungkan dengan polinomial order tiga (Gambar 1b). Rumus yang dihasilkan oleh integral di bawah polinomial tersebut dikenal dengan metode (aturan) Simpson.

Gambar 1. Aturan Simpson

A. Aturan Simpson 1/3

Gambar 2. Penurunan Metode Simpson

Di dalam aturan Simpson 1/3 digunakan polinomial order dua (persamaan parabola) yang melalui titik f (xi – 1), f (xi) dan f (xi + 1) untuk mendekati fungsi. Rumus Simpson dapat diturunkan berdasarkan deret Taylor. Untuk itu, dipandang bentuk integral berikut ini.

......(Persamaan 1)

Apabila bentuk tersebut didiferensialkan terhadap x, akan menjadi:

......(Persamaan 2)

Dengan memperhatikan Gambar 2 dan persamaan (2) maka persamaan deret Taylor adalah:

......(Persamaan 3)

......(Persamaan 4)

Pada Gambar 1, nilai I (xi + 1) adalah luasan dibawah fungsi f (x) antara batas a dan xi + 1. Sedangkan nilai I (xi - 1) adalah luasan antara batas a dan I (xi - 1). Dengan demikian luasan di bawah fungsi antara batas xi - 1 dan xi + 1 yaitu (Ai), adalah luasan I (xi + 1) dikurangi I (xi - 1) atau persamaan (3) dikurangi persamaan (4).

Ai = I (xi + 1) – I (xi - 1)

Atau,

......(Persamaan 5)

Nilai f(xi) ditulis dalam bentuk diferensial terpusat:

Kemudian bentuk diatas disubstitusikan ke dalam persamaan 5. Untuk memudahkan penulisan, selanjutnya notasi f (xi) ditulis dalam bentuk fi, sehingga persamaan 5 menjadi:

atau

......(Persamaan 6)

Persamaan 6 dikenal dengan metode Simpson 1/3. Diberi tambahan nama 1/3 karena delta x dibagi dengan 3. Pada pemakaian satu pias, sehingga persamaan 6 dapat ditulis dalam bentuk:

......(Persamaan 7)

dengan titik c adalah titik tengah antara a dan b. Kesalahan pemotongan yang terjadi dari metode Simpson 1/3 untuk satu pias adalah:

Oleh karena , maka:

---

Secara garis besar kaidah simpson adalah sebagai berikut :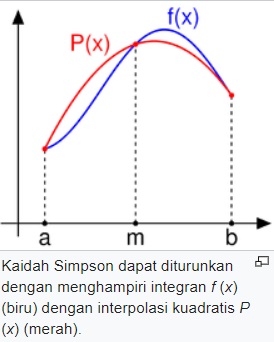

Dengan perumusan kaidah sebagai berikut :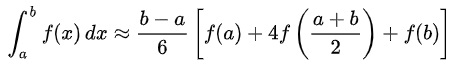

---

B. Aturan Simpson 1/3 dengan banyak pias

Seperti dalam metode trapesium, metode Simpson dapat diperbaiki dengan membagi luasan dalam sejumlah pias dengan panjang interval yang sama (Gambar 3): dengan n adalah jumlah pias

Gambar 3. Metode Simpson dengan banyak pias

Luas total diperoleh dengan menjumlahkan semua pias, seperti pada Gambar 3.

......(Persamaan 8)

Dalam metode Simpson ini jumlah interval adalah genap. Apabila persamaan 6 disubstitusikan ke dalam persamaan 8 akan diperoleh:

atau,

......(Persamaan 9)

Seperti pada Gambar 3, dalam penggunaan metode Simpson dengan banyak pias ini jumlah interval adalah genap. Perkiraan kesalahan yang terjadi pada aturan Simpson untuk banyak pias adalah:

dengan adalah rerata dari turunan keempat untuk setiap interval.

C. Metode Simpson 3/8

Metode Simpson 3/8 diturunkan dengan menggunakan persamaan polinomial order tiga yang melalui empat titik. Dengan cara yang sama pada penurunan aturan Simpson 1/3, akhirnya diperoleh:

......(Persamaan 10)

Dengan,

Persamaan 10 disebut dengan metode Simpson 3/8 karena x dikalikan dengan 3/8. Metode Simpson 3/8 dapat juga ditulis dalam bentuk:

......(Persamaan 11)

Metode Simpson 3/8 mempunyai kesalahan pemotongan sebesar:

......(Persamaan 12a)

Mengingat , maka:

......(Persamaan 12b)

Metode Simpson 1/3 biasanya lebih disukai karena mencapai ketelitian order tiga dan hanya memerlukan tiga titik, dibandingkan metode Simpson 3/8 yang membutuhkan empat titik. Dalam pemakaian banyak pias, metode Simpson 1/3 hanya berlaku untuk jumlah pias genap. Apabila dikehendaki jumlah pias ganjil, maka dapat digunakan metode trapesium. Tetapi metode ini tidak begitu baik karena adanya kesalahan yang cukup besar. Untuk itu kedua metode dapat digabung, yaitu sejumlah genap pias digunakan metode Simpson 1/3 sedang 3 pias sisanya digunakan metode Simpson 3/8.