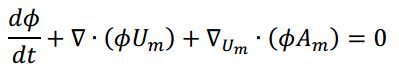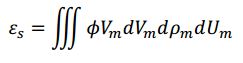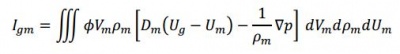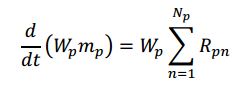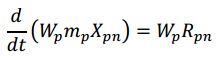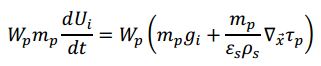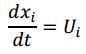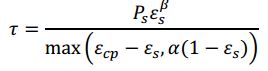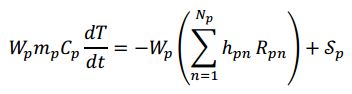MMPIC
1.Background
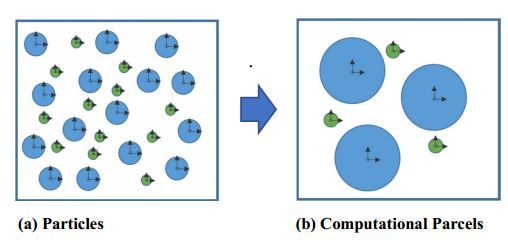
The MMPIC solids model tracks the position and trajectory of computational parcels, statistical groups of particles that share the same physical characteristics (e.g. diameter and density). In the present formulation, different diameter particles of the same material must be defined as separate solid phases, each with its own statistical classification. Figure 1 illustrates this idea.
Figure 1: Visual concept of particle consolidation to computational parcels by type. (a) A single cell populated with particles. (b) The same single cell after a statistical weight has been applied to each particle type.
If one imagines that Figure 1 represents a single cell, there are 15 blue particles represented by 3 blue computational parcels, and 12 green particles represented by 3 green computational parcels. In simple terms, 1 blue parcel carries a statistical weight of 5 particles/parcel, and 1 green parcel carries a statistical weight of 4 particles/parcel. Figure 1 one can immediately perceive the natural solution degradation that is inherent to this kind of statistical consolidation of particles. For example, the method must immediately lose the precise physics associated with particle-to-particle contacts and instead use more generalized representations of particle interactions. In particular, without resolving particle collisions or managing Newtonian mechanics in any way, the PIC model creates an aggregated solids stress momentum source term that affects local solids velocity directly. Snider (2001) refers to this source term as a frictional stress model.
The frictional stress model is driven by an evaluation of local solids volume fraction gradient and averaged field quantities. This statement implies that the model implementation is algebraic, and therefore computationally efficient. Consequently, the PIC model can deliver computational predictions for suitable large industrial applications intractable wall time. Aside from the frictional stress model, the PIC can support subsidiary models (e.g. a collisional stress model, wall friction models) that may add to the fidelity of results. As with all coupled computational fluid dynamics (CFD) simulations, these subsidiary models will add time to the solution.
2.Assumption
a. Particles are assumed spherical in shape within computational parcels. Why? Subsidiary models used in the formulation of pre-assume particles are spherical such as Wen-Yu, Gidaspow, Gidaspow-Blend, or Syamlal-O’Brien drag models, Likewise, any surface area or volume-dependent calculations rely on the radial (assumed sphere) definition, like chemical reactions.
b. Computational parcels must be defined by phase and maintain a mean density. Why? Subsidiary calculations for drag, thermal transfer, and chemical reaction rely on particle-level definitions. This allows for more simple calculations of particle diameter within each tracked parcel. For example, when density is assumed constant, and a chemical reaction takes place, a new particle diameter (within the parcel) can be calculated to reflect a mass gain/loss. Simply, accounting is easier (and faster) with this assumption.
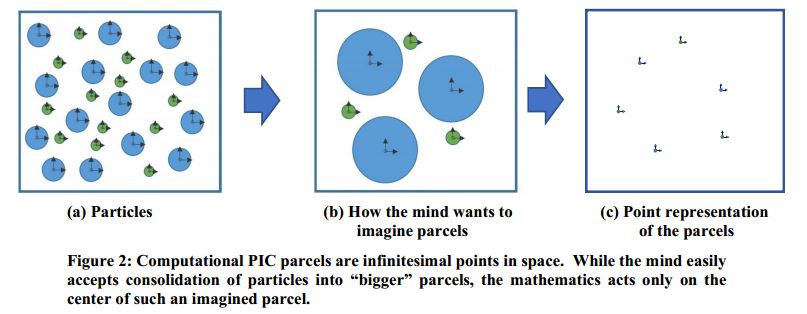
c. Computational parcels are isothermal. Why? To maintains no physical representation of how particles might populate a parcel. Mathematics treats each PIC parcel as a single point in space. There are no particle or parcel surfaces or other 3-dimensional physical features on which to act. The imagined surfaces of the computational parcels are irrelevant to the mathematical model. Figure 2 illustrates how the mind wants to give computational parcels structure
d. Computational parcels do not experience rotation. Why? Figure 2 illustrates the point representation of parcels in PIC. Points cannot experience rotation.
e. There are no formally modeled collisions; parcels may pass freely through each other when velocity fields warrant motion.
f. The PIC method is inappropriate for use in very dilute flows; a single parcel is the least amount of solids representative in any single cell, based on initial conditions. Why? The model requires the formation of solids fraction gradients to create estimates of changes in solids velocity. In very dilute flow (and at fully dense pack flows), the solids fraction gradients in a simulation will approach zero2. When this happens, the PIC may predict no solids movement (with respect to other solids) and subtle flow changes become indiscriminate. For cases that involve very dilute flow or very dense nearly close-packed flows, loss of accuracy in those areas is expected.
g. Parcels interact with walls through 3-dimensional reflection. Why? Again, because no formal parcel geometry is maintained, and only a center point is known, a point reflection method is applied to parcels at the walls.
h. The method is not formulated for 2-dimensional simulation.
3. Multiphase particle in cell (MPPIC)
The multiphase particle-in-cell (MP-PIC) numerical method for predicting dense gas-solids flow. The MP-PIC method is a hybrid method such as IBM method, where the gas-phase is treated as a continuum in the Eulerian reference frame and the solids are modeled in the Lagrangian reference frame by tracking computational particles. The MP-PIC is a derivative of the Particle-in-Cell (PIC) method for multiphase flows and the method employs a fixed Eulerian grid and Lagrangian parcels are used to transport mass, momentum, and energy through this grid in a way that preserves the identities of the different materials associated with the particles. The main distinction with traditional Eulerian-Lagrangian methods is that the interactions between the particles are calculated on the Eulerian grid. The Eulerian-Lagrangian method and the multiphase particle in cell (MPPIC) method have been used in this study. The model of the MPPIC is a Model Collision in CFDSOF, first of all, PIC models are derived from a Liouville equation describing the time evolution of a particle distribution function.
where X is particle position, ܷUm is particle velocity, p m is particle density, ܸ Vm is particle volume, and t is time. The subscript ݉m is indicative of nodding to solids phase ݉, which in this case would indicate a unique solids class of particles.
Here ∇ um is the divergence operator with respect to the velocity, ܷUm and A m is the discrete particle-phase acceleration. The particle distribution function integrated over velocity and mass will yield the likely number of particles per unit volume at the position, X, at time t, for small intervals of (Vm + dVm, pm + dpm, Um + dUm). The solids volume fraction, Es, can then by represented through the distribution function using a volume integral.
The solids phase is coupled to the Eulerian governing equations through the interphase momentum transfer term. Allowing Igm to be the contribution due to interphase momentum transfer between the gas and the m th solid phase, Where Dm is drag coefficient and ∇ p is pressure gradient.
4. Conservation Equation
The word particle, a single piece of material, spherical in nature, having physical characteristics that can be uniquely defined (like density, chemical composition, etc.); the word parcel indicates a statistical collection of particles of similar physical characteristics.
Conservation of Mass
The conservation of mass (or continuity equation) for the p th MPPIC parcel is given by managing the particle’s statistical weight, Wp, and considering its mass change, dm/dt, under the effects of a chemical reaction.
where R pn is the rate of production/consumption of the n th chemical species, and Np is the number of chemical species. This is not unlike the conservation of mass equation defined in Musser and Carney (2020). Specifically, the right-hand side of (eq above) accounts for interphase mass transfer because of heterogeneous chemical reactions or physical processes, like evaporation. In non-chemically reactive simulations (or those without phase change), the right side of Equation (eq above) equals zero.
Conservation of Species Mass
The n th species mass conservation equation for the MMPIC parcel is given by:
Where X pn is the n th chemical species mass fraction, and R pn is the rate of formation of species mass attributed to chemical reactions or physical processes. In non-chemically reactive simulations (or those without phase change), the right side of Equation (above) equals zero.
Conservation of Translational Momentum
The general conservation of translation momentum for the p th MMPIC parcel in the i th coordinate direction is given by:
where ܷU i is the parcel velocity, and ݃g i is the gravity body force. The first term on the right-hand side is the gravitational body force. The second term is a PIC-specific term derived from interparticle stress, described in detail in the section Interparticle Stress below.
As expected, the position of a parcel is related to its velocity through:
where Xi is the parcel position in the ݅i th coordinate direction.
Interparticle Stress
The interparticle stress variable follows the form suggested by Snider (2001). Specifically,
where E cp indicates a pre-determined, problem-specific, close-pack volume fraction for the solids phase. P s is an empirical pressure constant relatable to the scale and unit of the problem under evaluation, and B is an empirical unitless exponent, usually between 2 and 5. alpha is a tiny constant (e.g. 1e-7) to assure a non-zero denominator in calculations.
Conservation of Internal Energy
The general conservation of internal energy for the p th MMPIC parcel follows the same theoretical underpinnings as DEM. The internal energy is presented in terms of temperature. For an isothermal parcel (a PIC assumption),
where C p and ܶT are parcel specific heat and temperature (same as particle values). The first term on the right-hand side represents changes in internal energy accompanying species formation or destruction from a chemical reaction and/or phase change (h pn is the n the species-specific enthalpy) The last term, S p is a general source term. Note that S p might represent particle-particle heat transfer (currently 0 in PIC; there is no conduction model), fluid-particle heat transfer (convection), or radiative heat transfer (currently 0 in PIC; radiation model is pending).