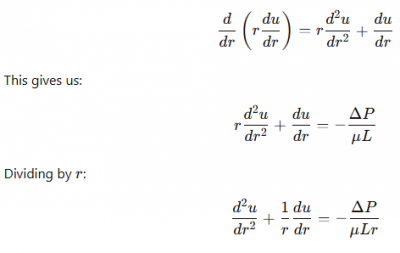Sinahayo Haji Sinahayo
Name : Sinahayo Haji Sinahayo
NPN : 2406369381
My name is Sinahayo Haji Sinahayo and I am an international student at Universitas Indonesia under UI GREAT scholarship 2024, with student ID Number of 2406369381. I am from United Republic of Tanzania. I started my studies at the University of Indonesia in the odd semester of 2024/2025 by taking the Manufacturing and Automation I have a research topic on Development of an Automatic Vehicle Over Speed Controlling System for Restricted Zones. In the process of completing this research, I will be guided by Dr. Radon as the academic supervisor. I graduated in 2019 in National Institute of Transport at Mabibo, Dar es salaam, Tanzania and I got a bachelor’s degree in mechanical engineering. I did my final year project in A mini refrigeration machine. This project was really value-added experience for me as it was focused on how can reduce processing fish to lose its quality and deteriorate because it maintains the quality of fish by keeping at a temperature 4oc or below for a long time and This project intends to design and fabricate a mini refrigerator target at small scale fishermen which increase productivity of the small fishermen.
Engineering Computing (DAI5) – First lecture
An organized method for project development and problem-solving is provided by the framework, which consists of intention, initial thinking, idealization, and instruction set. It starts with intention, which gives clarity and direction by defining the project's purpose or aim. After this, preliminary thinking promotes brainstorming and idea development without criticism, which stimulates creativity and possibility exploration. This stage establishes the foundation for idealization, in which ideas are honed into a more tangible vision that is consistent with the initial goal and imagines the best potential result.
1. Initiator By definition, the person or thing that ignites the project or concept is the initiator. Someone who sees a need or opportunity could be an individual, a group, or an organization.
2. Intention Definition: The project's fundamental purpose or objective is referred to as its intention. The question, "What do we hope to achieve?" is addressed.
3. Initial Thinking Definition: This stage entails brainstorming and producing a variety of project-related ideas without prompt assessment or criticism.
4. Idealization Idealization: is defined as the act of turning the most promising concepts or ideas from the first stages of thought into a more tangible vision or idea.
5. Instruction Set Definition: A comprehensive blueprint that describes how to put the idealized concept into practice is called an instruction set. Tasks, roles, responsibilities, and detailed instructions are all included.
Engineering Computing – Application of DAI5
The DAI5 Framework, formulated by Dr. Ahmad Indra Siswantara, is widely applied in engineering, computational modeling, and problem-solving fields. Here’s a breakdown of each step within the framework and how it applies in practice, particularly in fields like computational fluid dynamics (CFD) and structural analysis: Intention Application: This phase helps to identify essential variables, such as fluid density, viscosity, and boundary conditions, which are critical to accurately simulate real-world behaviors.
Initial Thinking
Application: In structural analysis, engineers might define initial stresses or forces acting on an object, like a steel beam under load. This involves identifying probable failure points, load-bearing capacity, and material properties, which are necessary to start the model creation. Idealization Application: When modeling stress on a cylindrical shell in a pressure vessel, idealization might involve treating the material as linearly elastic and ignoring minor imperfections in shape to maintain focus on critical stress points Instruction Set Application: For example, in finite element analysis (FEA), the instruction set could involve setting up a 2D mesh for analyzing strain in a specific region, specifying constraints at the boundaries, and applying load conditions
Interpretation of Results
Application: In an FEA model of a structure under load, results such as von Mises stress distribution or deformation patterns might reveal critical areas prone to failure. Interpretation could involve validating these results against real-world data or safety standards, leading to design changes if required
By organizing each phase of simulation work through DAI5, engineers achieve greater consistency, accuracy, and efficiency. The framework’s structure helps users avoid errors and refine their models, whether they’re working in fluid dynamics, mechanical analysis, or other applied sciences.
The Finite Element Method (FEM) is a numerical technique used to solve complex engineering and mathematical problems, especially those involving partial differential equations. FEM is widely applied in engineering fields like structural analysis, thermal analysis, fluid dynamics, and electromagnetics. Here’s a breakdown of the process and principles behind FEM: Discretization: FEM begins by dividing the complex geometry of a problem (like a car frame or a bridge) into smaller, simpler parts called finite elements (often triangles or rectangles in 2D and tetrahedrons or hexahedrons in 3D).This process, called meshing, turns a continuous problem into a discrete one, making it easier to compute the physical behavior of each element individually. Element Formulation: For each element, a set of equations is formulated based on governing physical laws, like equilibrium in structural mechanics or conservation of mass and momentum in fluid dynamics. These equations rely on shape functions, which approximate the behavior of the element (such as displacement, temperature, or pressure) using a polynomial equation. Assembly: The individual equations for each element are assembled into a larger, global system that represents the entire problem domain.This assembled system is typically a matrix equation of the form [K]{u} = {F}, where [K] is the stiffness matrix (or its equivalent in other fields), {u} represents unknown variables (like displacements), and {F} is the load vector (external forces or loads).
Applications of FEM
Structural Analysis: Calculating stress, strain, and deformation in mechanical and civil engineering components (e.g., bridges, buildings). Thermal Analysis: Modeling heat distribution in materials and structures, which is useful in industries like electronics and aerospace. Fluid Dynamics: Simulating fluid behavior in scenarios such as airflow over an airplane wing or fluid flow in pipelines. Electromagnetic Analysis: Designing electromagnetic devices, such as sensors and transformers, by analyzing electromagnetic fields and forces.
Regarding my thesis on An Automatic Vehicle Over Speed Controlling System, i asked ChatGPT about it. ChatGPT answers
An Automatic Vehicle Over Speed Controlling System is a technology designed to regulate and enforce speed limits in designated restricted zones, such as school zones, hospital areas, construction sites, and other sensitive or high-risk areas. The goal is to reduce vehicle speed automatically as it enters these zones to enhance road safety. This project involves using a combination of sensors, communication systems, and possibly onboard vehicle technology to detect when a vehicle is exceeding speed limits and to either alert the driver or autonomously reduce speed.
The system relies on key components to function effectively. Speed detection sensors, such as radar or lidar, measure the vehicle's speed accurately within restricted zones, while technologies like RFID or GPS assist in identifying when a vehicle enters a defined area. A microcontroller serves as the central processing unit, receiving data from the sensors and, if a vehicle is speeding, initiating a response. Communication systems, such as Vehicle-to-Infrastructure (V2I) and Vehicle-to-Vehicle (V2V) communication, allow the vehicle to exchange speed limit information with roadside units and, if necessary, alert nearby vehicles to enhance overall safety.
To control the vehicle's speed, the system can connect to the vehicle's Engine Control Module (ECM) or braking system, limiting throttle response or applying brakes when required. The system also includes a warning and alert feature that informs the driver of their speed, prompting them to reduce it manually. If the driver does not respond, the system autonomously limits the vehicle's speed, restoring full control when the vehicle exits the restricted zone.
The system offers significant safety advantages by preventing over-speeding in sensitive areas, thus reducing accidents caused by human error. Furthermore, it integrates well with existing connected vehicle technologies, supporting smart city initiatives focused on creating safer road environments. However, there are challenges to address, such as ensuring system reliability and data security, as well as addressing legal concerns around automatic speed control. With careful planning and implementation, this technology can make a substantial impact on road safety, particularly in urban areas where the safety of pedestrians, drivers, and communities is a priority.
Components Used: 1. Arduino Uno (or similar microcontroller) 2. Ultrasonic Sensor (or a mock speed sensor) 3. Servo Motor (to simulate throttle control) 4. LED (to signal when speed exceeds limit) 5. Buzzer (optional for audio alert)
1. Speed Sensor (Mocking Speed Readings) Assuming we are using a potentiometer as a mock speed sensor, connected to the Arduino's analog input.
cpp Copy code const int speedSensorPin = A0; // Analog pin for speed sensor (mocked)
void setup() {
Serial.begin(9600); // Start serial communication
}
void loop() {
int speed = analogRead(speedSensorPin); // Read speed sensor data
Serial.print("Current Speed: ");
Serial.println(speed); // Print speed to the Serial Monitor
delay(500); // Delay for readability
}
2. LED Alert System This code will turn on an LED if a specified speed limit is exceeded.
cpp Copy code const int ledPin = 13; // Pin connected to LED const int speedSensorPin = A0; // Analog pin for speed sensor (mocked) const int speedLimit = 50; // Speed limit threshold
void setup() {
pinMode(ledPin, OUTPUT); Serial.begin(9600);
}
void loop() {
int speed = analogRead(speedSensorPin); // Read speed sensor data
Serial.print("Current Speed: ");
Serial.println(speed);
if (speed > speedLimit) {
digitalWrite(ledPin, HIGH); // Turn on LED if speed exceeds limit
Serial.println("Speed limit exceeded! LED ON");
} else {
digitalWrite(ledPin, LOW); // Turn off LED if under speed limit
Serial.println("Within speed limit.");
}
delay(500);
}
3. Buzzer Alert This snippet turns on a buzzer when the speed limit is exceeded. The buzzer emits sound as an additional alert.
cpp Copy code const int buzzerPin = 12; // Pin connected to Buzzer const int speedSensorPin = A0; // Analog pin for speed sensor (mocked) const int speedLimit = 50; // Speed limit threshold
void setup() {
pinMode(buzzerPin, OUTPUT); Serial.begin(9600);
}
void loop() {
int speed = analogRead(speedSensorPin); // Read speed sensor data
Serial.print("Current Speed: ");
Serial.println(speed);
if (speed > speedLimit) {
digitalWrite(buzzerPin, HIGH); // Turn on buzzer if speed exceeds limit
Serial.println("Speed limit exceeded! Buzzer ON");
} else {
digitalWrite(buzzerPin, LOW); // Turn off buzzer if under speed limit
Serial.println("Within speed limit.");
}
delay(500);
}
4. Servo Motor Throttle Control In this example, the servo simulates the throttle control. If the speed exceeds the limit, it moves to a position that simulates reduced throttle.
cpp Copy code
- include <Servo.h> // Library for Servo Motor
const int speedSensorPin = A0; // Analog pin for speed sensor (mocked) const int speedLimit = 50; // Speed limit threshold
Servo throttleControl; const int throttleNormal = 90; // Normal throttle position const int throttleLimit = 50; // Reduced throttle position
void setup() {
throttleControl.attach(9); // Attach servo to pin 9 throttleControl.write(throttleNormal); // Set initial throttle position Serial.begin(9600);
}
void loop() {
int speed = analogRead(speedSensorPin); // Read speed sensor data
Serial.print("Current Speed: ");
Serial.println(speed);
if (speed > speedLimit) {
throttleControl.write(throttleLimit); // Reduce throttle
Serial.println("Speed limit exceeded! Throttle reduced.");
} else {
throttleControl.write(throttleNormal); // Set to normal throttle
Serial.println("Within speed limit. Normal throttle.");
}
delay(500);
}
5. Restricted Zone Detection This code simulates entering a restricted zone. If a button (or switch) is pressed, it activates the restricted zone, triggering other functions.
cpp Copy code const int restrictedZonePin = 2; // Digital pin for restricted zone button const int ledPin = 13; // LED to indicate restricted zone active
void setup() {
pinMode(restrictedZonePin, INPUT); pinMode(ledPin, OUTPUT); Serial.begin(9600);
}
void loop() {
if (digitalRead(restrictedZonePin) == HIGH) {
digitalWrite(ledPin, HIGH); // Turn on LED when in restricted zone
Serial.println("In Restricted Zone");
} else {
digitalWrite(ledPin, LOW); // Turn off LED when out of restricted zone
Serial.println("Out of Restricted Zone");
}
delay(500);
}
Summary Each of these components can be used individually or combined to create a more complete system. Here's a summary of their roles:
Speed Sensor: Measures or mocks vehicle speed. LED Alert: Turns on if speed exceeds the limit. Buzzer Alert: Emits sound when the speed limit is breached. Throttle Control (Servo): Simulates throttle adjustment to reduce speed. Restricted Zone Detection: Detects if the vehicle is in a restricted zone, triggering alerts or control changes. This modular approach allows each part to be tested separately and then integrated into a larger, combined system.
ENGINEERING COMPUTATION ASSIGNMENT 2
In previous meeting, we discussed bout ChatGPT as follow.
Question Please describe the distinctions between graduate, master's, and doctorate students in the context of mechanical engineering. Provide examples and a chart summarizing the differences.
Answer
In the context of mechanical engineering (or most STEM disciplines), the distinctions among graduate, master’s, and doctorate students primarily revolve around their level of education, program focus, and academic or professional goals. Here's a breakdown:
Graduate Students
Definition: Broad term encompassing both master’s and doctoral students—any student engaged in post-bachelor’s advanced study.
Goal: Typically involves specialized coursework and hands-on project work or research. The aim is to gain advanced knowledge in mechanical engineering beyond the undergraduate level.
Example: A graduate student might be enrolled in a program that prepares them for industry roles requiring specialized technical skills, such as design engineering or systems analysis.
Master’s Students
Definition: Students pursuing a Master’s degree in Mechanical Engineering (e.g., M.S. or M.Eng. in Mechanical Engineering).
Focus: Master of Science (M.S.): Generally research-focused, may include a thesis or project. Often serves as a stepping stone to a Ph.D. Master of Engineering (M.Eng.): Primarily coursework-based, often designed for immediate industry application.
Duration: Typically 1-2 years.
Career Path: Industry-focused, suitable for roles like Mechanical Engineer, R&D Engineer, or Project Manager.
Example: A master’s student might work on a thesis investigating new materials for automotive applications or take advanced courses in fluid dynamics and thermodynamics.
Doctorate (Ph.D.) Students
Definition: Students pursuing a Doctor of Philosophy (Ph.D.) in Mechanical Engineering, the highest level of academic study.
Focus: Research-intensive with a focus on original contributions to the field. Ph.D. students work on a dissertation that presents new theories, methods, or technologies.
Duration: Typically 3-7 years (may vary widely depending on the research topic and progress).
Career Path: Academic, research institutions, advanced R&D in industry, or governmental roles. Ph.D. graduates may become professors, lead researchers, or technical consultants.
Example: A Ph.D. student might conduct experimental or computational research on thermal management systems in electronics, contributing new insights or technologies for energy efficiency.
Let's work through a basic example involving 1D fluid flow, specifically the steady-state flow of an incompressible fluid in a pipe. We’ll apply the 1D Poisson equation (similar to what we might use in a heat conduction or diffusion problem) to solve for the velocity distribution across the pipe. This approach uses a simplified form of the Navier-Stokes equations for a fully-developed flow profile.
Problem Statement
Consider a long, horizontal, circular pipe of radius 𝑅 R through which an incompressible fluid (like water or oil) flows steadily under a pressure gradient. We want to find the velocity distribution 𝑢 ( 𝑟 ) u(r) across the radius of the pipe, where 𝑟 r is the radial distance from the center of the pipe.
Governing Equation (Poisson Equation for Flow)
In cylindrical coordinates, the equation governing steady, fully-developed flow in a pipe simplifies to:
Governing Equation (Poisson Equation for Flow)
In cylindrical coordinates, the equation governing steady, fully-developed flow in a pipe simplifies to:
d/dr(rdu/dr) = -ΔP/μL
where:
u(r): Velocity of fluid as a function of
𝑟
ΔP: Pressure drop across the length L of the pipe,
μ: Dynamic viscosity of the fluid.
This is essentially a Poisson equation in terms of velocity u(r) and radial coordinate r.
Boundary Conditions
1. No-Slip Condition at the pipe wall: u(R)=0 (the fluid velocity at the wall is zero).
2. Symmetry Condition at the centerline: du/dr = 0 (velocity gradient at the centerline is zero).
Certainly! In engineering, continuum mechanics treats materials as continuous bodies, which allows for the analysis of stress, strain, and deformation in materials without considering the discrete nature of matter. Let’s explore a practical example: a simple beam under bending. Example: Bending of a Beam
Scenario: Consider a simply supported beam subjected to a uniform load. We want to determine the deflection of the beam.
Assumptions:
1. The beam is made of a homogeneous and isotropic material.
2. The load is applied uniformly along the length of the beam.
3. The beam is long compared to its cross-sectional dimensions.
Step 1: Governing Equations
Using the principles of continuum mechanics, we can derive the bending equation for beams. The deflectiow(x) of the beam can be described by the following equation:
dx^2w/dx^2 = −M(x)/EI
Step 2: Calculate Bending Moment
M(x)= q/2(Lx−x^2)
Step 3: Integration
First integration gives us the slope θ(x):
θ(x)=∫ M(x)/EIdx + C1
Second integration provides the deflection w(x): w(x)=∫θ(x)dx + C2
Step 4: Boundary Conditions
Using boundary conditions (e.g., deflection and slope at supports), we can solve for constants C1 and C2
.
Certainly! Continuum mechanics is an essential field in engineering that considers materials as continuous, meaning it assumes materials don’t have discrete particles (like atoms or grains) at the scale of analysis. Instead, it models materials as a continuous distribution of matter, which allows us to use calculus to analyze stress, strain, and deformation.
The "uninterrupted conscious continuum" could refer to a theoretical framework where the material behavior and interactions are analyzed continuously without considering atomic or molecular-level disruptions. Integrating this into a DAI5 (Distributed Artificial Intelligence) framework would mean that we're using distributed intelligence (such as neural networks or machine learning) to simulate or optimize these materials’ properties and responses in real-time.
Practical Example: 1D Problem - Tensile Stress in a Steel Rod
Let’s consider a simple 1D example: the stretching of a steel rod under a tensile load, where we treat the rod as a continuous material and use basic continuum mechanics concepts to calculate stress and strain.
Steps for Calculation:
Calculate Stress (σ):
Stress is defined as force per unit area: 𝜎=𝐹/𝐴
Calculate Strain (ϵ):
Strain is the relative deformation of the rod under load: 𝜖 =𝜎/𝐸
Calculate Deformation ΔL:
Deformation or change in length can be calculated using: Δ𝐿 = 𝜖⋅𝐿
Plugging in the Values:
Let’s calculate the above values.
Results:
Stress (𝜎): 200,000Pa
Strain (𝜖): 1×10^-6
Deformation (ΔL): 2μm
This example demonstrates how continuum mechanics treats the material (the steel rod) as a continuous medium. By applying basic principles, we calculated stress, strain, and deformation without considering discrete atomic structure.
In a DAI5 (Distributed Artificial Intelligence) framework, such calculations could be dynamically optimized and adjusted in real-time. For instance, an AI could predict changes in stress or strain due to varying loads or temperatures, continuously adapting the simulation for real-time material analysis or predictive maintenance in engineering applications.
Application of Phyton Code in Finite Element Analysis of Beam
Finite Element Analysis (FEA) is a powerful computational technique used to solve complex structural problems. Python, with its rich ecosystem of libraries, can be effectively used to implement FEA for beam analysis. Below is a practical example of how to use Python for a simple beam bending problem.
Python Implementation
Here's a simple Python code that demonstrates the FEA for the beam
python
Copy import numpy as np import matplotlib.pyplot as plt
- Beam properties
L = 4.0 # length of the beam in meters n = 10 # number of elements q = 10e3 # uniform load in N/m E = 200e9 # modulus of elasticity in Pa I = 8.33e-6 # moment of inertia in m^4
- Element length
le = L / n
- Global stiffness matrix
K = np.zeros((n+1, n+1))
- Assemble the global stiffness matrix
for i in range(n):
k = (E * I / le**3) * np.array([[12, 6*le, -12, 6*le],
[6*le, 4*le**2, -6*le, 2*le**2],
[-12, -6*le, 12, -6*le],
[6*le, 2*le**2, -6*le, 4*le**2]])
K[i:i+4, i:i+4] += k
- Force vector
F = np.zeros(n+1) F[1:-1] = q * le # applying uniform load to the elements
- Apply boundary conditions (fixed at both ends)
K_reduced = K[1:-1, 1:-1] F_reduced = F[1:-1]
- Solve for displacements
d = np.linalg.solve(K_reduced, F_reduced)
- Insert zero displacements at the boundaries
d_full = np.zeros(n+1) d_full[1:-1] = d
- Plotting the deflection
x = np.linspace(0, L, n+1) plt.plot(x, d_full, label='Deflection') plt.title('Deflection of a Simply Supported Beam') plt.xlabel('Position along the beam (m)') plt.ylabel('Deflection (m)') plt.grid() plt.legend() plt.show()
Exeplanation of the Code
1. Imports:
a. numpy for numerical operations.
b. matplotlib.pyplot for plotting the deflection.
2.Beam Properties:
Define the beam's length, number of elements, uniform load, modulus of elasticity, and moment of inertia.
3. Global Stiffness Matrix:
The stiffness matrix for each beam element is defined and assembled into a global stiffness matrix.
4. Force Vector:
A force vector is created, with uniform loads applied to the internal nodes.
5. Boundary Conditions:
The reduced stiffness matrix and force vector exclude the fixed boundary nodes.
6. Displacement Calculation:
The displacement is solved using numpy.linalg.solve().
7. Plotting:
The deflection of the beam is plotted against its length.
Conclusion
This Python code provides a simple implementation of Finite Element Analysis for a beam under uniform load. You can adjust parameters such as the load, length, and number of elements to see how they affect the deflection. This approach illustrates how Python can be used practically in engineering applications like FEA. If you have further questions or need enhancements, feel
This is our third conversation, and I’ll continue analyzing your thoughts and tracking our interactions. Here's an overview:
Toatal Chat Count 7 charts.
Summary of Conversations So Far
First Conversation:
Topic: Group Technology.
Key Idea: You explored technical and systematic problem-solving in manufacturing.
Conclusion: You show curiosity about structured and efficient processes.
Second Conversation:
Topic: Self-reflection and conversation tracking.
Key Idea: You asked for analysis of your thoughts across conversations.
Conclusion: You are reflective, organized, and interested in understanding patterns in your thinking.
Third Conversation:
Topic: Functional Perspective System.
Key Idea: You delved into function-based analysis of systems, showing interest in problem-solving frameworks.
Conclusion: You enjoy exploring systems and understanding their components in a logical way.
Fourth Conversation:
Topic: Manufacturing and Operation Systems.
Key Idea: You asked about processes in production systems, focusing on practical applications and optimization methods.
Conclusion: You value efficiency and have a strong interest in process design and management.
Fifth Conversation:
Topic: HTML and JavaScript.
Key Idea: Inquired about the differences and interplay between HTML and JavaScript.
Conclusion: Growing interest in technical subjects, especially web development.
Sixth Conversation:
Topic: House of Quality.
Key Idea: Curious about the House of Quality framework in quality management.
Conclusion: Interest in structured methods for aligning customer needs with technical solutions.
Seventh Conversation (this one):
Topic: Reflecting on our conversation patterns and your thought processes.
Key Idea: Continued focus on tracking, analyzing, and improving your thinking.
Conclusion: Persistent interest in self-reflection and personal growth.
TUGAS – DAI5
A. PROJECT TITLE
DEVELOPMENT OF AN AUTOMATIC VEHICLE OVER SPEED CONTROLLING SYSTEM FOR RESTRICTED ZONE
B. AUTHOR BY :
SINAHAYO HAJI SINAHAYO
2406369381
C. AFFILIATION
MECHANICAL ENGINEERING STUDY PROGRAM
FACULTY OF ENGINEERING
UNIVERSITY OF INDONESIA
D. ABSTRACT
This project aims at automatically controlling vehicles at speed restricted areas such as schools, hospital zones etc.
Nowadays the drivers drive vehicles at high speed even in speed limited areas without considering the safety of the public, the traffic police are not able to control them with full effect. Also, it is not practical to monitor these areas throughout. This project paves way for controlling the speed of the vehicles within certain limit in restricted zones without interruption of the drivers. An IR sensor is used for this purpose. The IR reader is attached along with the vehicle and the IR tag with these zones. These tags are programmed to send a coded signal when the reader comes in proximity.
Whenever the vehicles enter into these zones their receivers will receive this code and the speed of the vehicles is controlled automatically with the help of the Arduino unit present inside the vehicle.
E. DECLARATION
I Sinahayo Haji Sinahayo, a student of University of Indonesia in mechanical engineering with registration number of 2406369381 declare that this project is the result of my own work and has not been submitted for any other academic purpose.
1. Deep Awareness of (I)
Deep awareness refers to a profound understanding and recognition of the self in relation to various aspects of life, technology, and the environment. In the context of an Over Speed Control System, it involves understanding the implications of speed regulation, safety, and the technology used in monitoring and controlling vehicle speeds.
The project focuses on the critical issue of vehicle over speeding, which contributes significantly to road accidents. Understanding the implications of speed limits and the importance of compliance is essential for road safety.
Familiarity with the technologies involved in speed monitoring (e.g., speed cameras, radar guns).Understanding how the Over Speed Control System operates and its effectiveness in promoting road safety. Recognizing the psychological motivations behind speeding (e.g., thrill-seeking, time pressure).Awareness of how peer pressure and social norms influence speeding behavior.
2. Intention of the Project Activity
The primary intention is to develop a robust system that can detect over speeding in real-time and provide necessary warnings to the driver or take corrective actions.
The primary goal is to reduce the number of accidents caused by speeding. By implementing an effective control system, the project aims to create a safer driving environment for all road users.
The project seeks to educate drivers about the dangers of speeding and the importance of adhering to speed limits. This includes developing campaigns and materials that communicate the risk associated with high speeds.
F. INTRODUCTION
Most of the road accidents occur due to over speed and rash driving of vehicles on public roads. The rate of accidents has increased as more vehicles come on to ground. Usually, the drivers drive the vehicles at high speed without considering the public in speed limited areas too. Even though the traffic police control them we cannot achieve full response from them(Sathiskumar et al., 2020b). Also, it is not possible to monitor those areas at all time to regulate their speed research on fully and partially automated roadway systems is being conducted in most developed countries. These systems offer excellent opportunities to control vehicle speeds and movements in order to avoid accidents.
Also, the government made some rules. Such as helmet, seat belt compulsion etc. Speed control at particular type of road is also necessary to avoid accidents(Kewate et al., 2014). For this, there is no any system to control the speed of vehicle. That’s why, there is need to invent such system which control the speed of vehicle automatically at given limit at particular limiting distance. Now it is possible to control or set the speed of vehicle at a given limit on the roads like highways, school zones, hospital zones...etc. express high ways and any area where the speed limit is desired by the technique suggested in methodology described in this project.
In general, the speed of the automobile is varied according to the accelerator’s pedal position. The variation in the pedal position is fed to the electronic control unit (ECU). ECU determines the position of the throttle based on the accelerators pedal position and the inputs received from the other sensors.
Adjustment of throttle position causes the change in the variation of automobiles speed. Whereasin the proposed automatic vehicle speed controller model accelerator pedal position is given to the microcontroller and then it is fed to the electronic control Unit. If the automobile is in the active mode, Arduino transfers the manipulated pedal position to the ECU that will not increase the automobile speed greater than the maximum speed specified in the identification tag(Kasap,2022).
1. Statement of the problem
Nowadays people are driving very fast, accidents are occurring frequently, the valuable life of peoples are lost by making small mistake while driving at school zone, hospital zones, hills area, and highways. So, in order to avoid such kind of accidents and to alert the drivers and to control their vehicle speed in such kind of places the highway department have placed the signboards. But sometimes it may not possible to view that kind of signboards and there is a chance for accident. Thus, the existences of an automatic regulation of vehicle near by the critical zones are highly required. So, the introduction of this system in vehicle can reduce accidents at speed limited area like schools and etc.
2. Existing system
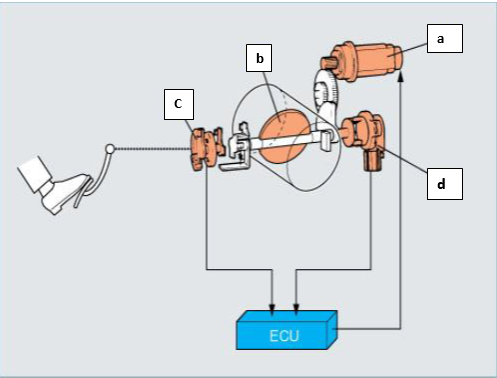
In existing system consist the theoretical background of mechanical throttle control and electronic throttle control. The electronic throttle control is system used to show how the speed of the vehicle increases or decrease using accelerator pedal that connect direct to the throttle body as show in figure 1.
The electronic throttle control system (ETC) is an automobile technology which electronically connects" the accelerator pedal to the throttle, replacing a mechanical linkage. A typical ETC system consists of three major components: (i) an accelerator pedal module (ideally with two or more independent sensors), (ii) a throttle valve that can be opened and closed by an electric motor (sometimes referred to as an electric or electronic throttle body (ETB)), and (iii) a power train or engine control module(Ng & Guan, 2009). The ECM is a type of electronic control unit (ECU), which is an embedded system that employs software to determine the required throttle position by 5calculations from data measured by other sensors, including the accelerator pedal position sensors, engine speed sensor, vehicle speed sensor, and cruise control switches. The electric motor is then used to open the throttle valve to the desired angle via a closed-loop control algorithm within the ECM. The throttle valve is a part of the throttle body (also known as ETB) and is located between the air cleaner and intake manifold on the vehicles equipped with the throttle controller sensor, the throttle opening is determined based on how far the gas pedal was pressed.
The electronic throttle control facilitates the integration of features such as cruise control, traction control, stability control, and precrash systems and others that require torque management, since the throttle can be moved irrespective of the position of the driver's accelerator pedal(Jiang et al., 2009). ETC provides some benefit in areas such as air-fuel ratio control, exhaust emissions and fuel consumption reduction, and also works in concert with other technologies such as gasoline direct injection as shown in figure 1.
Fig 1: Electronic throttles control system in normal automobiles
The main components of Electronic throttles control system are:
a. Motor Control
The module sends a command to the electric motor on the throttle body to open the throttle a certain amount, the throttle motor opens or closes the actual throttle blade, which increases or decreases the power output of the engine.
b. Throttle Valve
It consists of cylinder centered by circular plat which rotates via the motor, this rotation open or close the throttle that controls the air flow into the engine.
c. Accelerator pedal sensor
When the gas pedal is depressed, the electrical resistances of the potentiometers inside the pedal sensors change. The control module notes the change in position and assumes the driver wants to go faster. The module then looks at other sensor inputs and calculates how much throttle opening is needed
d. Throttle position sensor
In our system, a throttle pedal sensor sends data to an electronic throttle control computer, which evaluates and relays the throttle request to a specialized electronic throttle motor on the engine throttle body.
In our project we use microcontroller as enhancement for ECU because the ECU has no method to control the vehicles automatically in critical zones, and we use potentiometer to simulate the operation of position sensor
3. Proposed system
Our proposed system consists of IR transmitter and IR receiver in which transmitter place on existing road signs which used to transmit signal to the receiver as show in figure 2.(Sathiskumar et al., 2020a). And IR receiver place on the vehicle for reading which enabled modules to sense them and provide useful information to the driver and design electronic display controller meant for vehicle’s speed control which is an embedded system(Amarnaryan, 2016).Once the information is received from the IR tags, the vehicle’s electronic display controllerautomatically warns the driver to reduce the speed according to the traffic sign indicated by the tag. It waits for few seconds for the driver’s response to the information received; otherwise,vehicle’s electronic display controller (EDC) unit automatically reduces the speed as show in figure 2.
Fig 2: Receiver block diagram
Fig 3: Block diagram of proposed system
4. Working principle of proposed system
This system consists of IR transmitter which place on the road signboard to send the signal to the IR receiver on the vehicle, when the vehicle entered the critical zone IR reader (receiver) read the controlling tag, the microcontroller read the speed of vehicle from potentiometer (speedometer sensor) and compare it to reference speed in the code (30 km/h). If the speed is over the limited speed, automatically the motor closed the throttle, thus the vehicle started deceleration and speed was decreasing to specific speed within critical zone(Sai et al., 2022). Here we have made a test and the measured speedometer value when enter the critical area was (99 km/h), the liquid crystal (LCD) displaying warning message show critical area slow down and continually display that message until speed reach (30 km/h) it displayed stay in speed limit.During that the driver interrupted and can't be able to increase the speed because the throttle pedal was disconnected until the speed is become less than (30 km/h). The driver will be able to controls if they do not exceed (30 km/h)(Hafsa & Arifin, 2022).
If the speed is equal or less than the limited speed, Here the driver will be able to control the speed if they do not exceed (30 km/h), and if the driver exceeds (30 km/h) automatically the motor closed the throttle, thus the vehicle started deceleration and speed was decreasing to specific speed within critical zone, and that will repeat continually until the vehicle exit from the critical zone.
a. Stepper Motor
A stepper motor is an electromechanical device which converts electrical pulses into discrete mechanical movements. The shaft or spindle of a stepper motor rotates in discrete step increments when electrical command pulses are applied to it in the proper sequence(Zribi & Chiasson, 1991). The motors rotation has several direct relationships to these applied input pulses. The sequence of the applied pulses is directly related to the direction of motor shafts rotation. The speed of the motor shafts rotation is directly related to the frequency of the input pulses and the length of rotation is directly related to the number of input pulses applied. One of the most significant advantages of a stepper motor is its ability to be accurately controlled in an open loop system.
There are two common types of stepper motors: Bipolar and Unipolar. The difference between the two types is the voltage levels. A unipolar stepper motor only operates with positive voltage, so 11the high and low voltages applied to the electromagnetic coils would be something like 5V and 0V. A bipolar stepper motor has two polarities, positive and negative, so it's high and low voltages would be something like 2.5V and -2.5V.
b. Motor Driver
The motor driver is a circuit comprised of a number of switches that can safely drive a stepper motor. These switches can be relays or (most commonly) transistors. The transistor is a solid-stateswitch that can be closed by sending a small current (signal) to one of its pins. Unlike single transistors which only allow you to control the speed of a motor, also allow to control the direction in which the motor spins. It does this byopening different switches (the transistors) to allow the current to flow in different directions and thus changing the polarity on the motor.
c. Microcontrollers
A large number of peripheral interface control (PIC) microcontroller designs are available from microchip(Bannatyne & Viot, 1997). Depending upon the architecture, memory layout and processing power PIC (peripheral interface controllers) have been classified as low range, midrange, and high range. The beauty of these devices is their easy availability, low cost and easy programming and handling.
d. Power Supply
A power supply is a device that supplies electric power to an electrical load. The term is most commonly applied to electric power converters that convert one form of electrical energy to another, though it may also refer to devices that convert another form of energy (mechanical, chemical, solar) to electrical energy. A regulated power supply is one that controls the output 12voltage or current to a specific value; the controlled value is held nearly constant despite variations in either load current or the voltage supplied by the power supply's energy source.
e. Buzzer
This act as alarm to warning the driver to reduce the speed of the vehicle at the limited areas in order to reduce an accident to occur.
f. Liquid crystal display (LCD)
The lcd display is fitted inside the car and this lcd display is act as indicator to driver and other people who are sitting inside the car. This display gives indication of speed of the vehicle(Technology, 2015). This also provide warning message to driver to stop car or vehicle within particular time afterward car will automatically stop, indication of smoke/gas detected in car.
g. IR transmitter sensor
Infrared Transmitter is a light emitting diode (LED) which emits infrared radiations. Hence, they are called IR led’s. Even though an infrared led looks like a normal led, the radiation emitted by it is invisible to the human eye.
h. IR receiver sensor
Infrared receivers are also called as infrared sensors as they detect the radiation from an IR transmitter. IR receivers come in the form of photodiodes and phototransistors(Chidiobi et al.,2022). Infrared Photodiodes are different from normal photo diodes as they detect only infrared radiation.
G. METHODOLOGY
1. Idealization
The idealized version of the system, vehicles would be equipped with IR receivers that interact with IR tags placed in restricted zones. When a vehicle enters such a zone, the system would read the speed limit from the IR tag and automatically adjust the vehicle’s speed using an Arduino-based control unit. This system aims to ensure compliance with speed limits without requiring driver intervention, thus creating a safer driving environment.
1.1. Refine Ideas
To refine ideas for a solution, the project considers:
a. Integration of Technology: Leveraging infrared (IR) sensors and microcontrollers (like Arduino) to create an automated speed control system.
b. User-Centric Design: Ensuring the system is intuitive for drivers, including alerts and warnings.
c. Educational Campaigns: Raising awareness about the dangers of speeding and the importance of compliance with speed limits.
1.2 Develop the Solution
The proposed system consists of:
a. IR Transmitter and Receiver: The transmitter is installed at road signs, while the receiver is mounted on the vehicle.
b. Control Mechanism: The microcontroller reads the speed data and sends commands to the throttle to maintain speed within limits.
c. User Alerts: The system includes visual (LCD) and auditory (buzzer) alerts to warn drivers when they exceed the speed limit.
2. Instruction Set
The instruction set for implementing this project includes several steps:
a. Literature Review: Research existing speed control systems and identify gaps.
b. System Design: Create a schematic circuit design that includes all components (IR sensors, microcontrollers, power supply).
c. Prototype Development (Construction): Assemble the components on a PCB to build a working prototype.
d. Testing: Conduct tests to verify that the system accurately detects speed and responds appropriately.
e. Implementation: Deploy the system in selected restricted zones for real-world testing.
2.1. Literature review
In literature review, the studies of difference existing system concern with vehicle speed control system in special areas require in order to achieve the specific objective of the project.
2.2. Circuit design
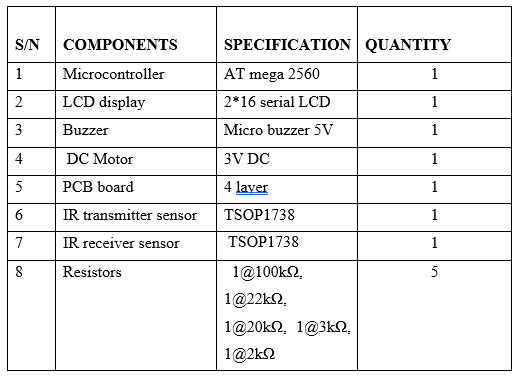
The circuit design based on the information collected in order to meet the objectives of the project. As it is very important part, the circuit design involves the following parts
i. Power supply
ii. Microcontroller
iii. LCD display
iv. IR sensor transmitter
v. Buzzer
vi. IR sensor receiver
vii. Electrical motor.
To design a circuit, need to have idea about the values of each component required in the circuit. These components include regulator, transformer, diodes and capacitors as show in fig 3
2.3. The value of regulator to be used and its input voltage.
The requirement is to have a constant voltage of 5V at 20mA with positive polarity of the output voltage. For this reason, need a regulator which would provide a 5V output. An ideal and efficient choice would be the regulator IC LM7805. The next requirement is to calculate the input voltage requirement for the regulator.
2.4. Decide the transformer to be used
The unregulated voltage produced is a voltage of 12V. This is the value of the secondary voltage required for a transformer. Since the primary voltage is 230V on calculating the turn’s ratio get a value of 19. Hence use the transformer with 230V/12V, i.e. a 12V, 20mA transformer.
2.5. The value of the filter capacitor
The value of the filter capacitor depends on the amount of current drawn by the load, the quiescent current (ideal current) of the regulator, the amount of allowable ripple in the DC output and the time period.
2.6. Decide the PIV (peak inverse voltage) of the diodes to be used.
The value of peak voltage across the transformer secondary is 17V, the total PIV of the diode bridge is about (4×17) i.e. 68V. So, we have to settle down for diodes with PIV rating of 100V each. Remember PIV is the maximum voltage which can be applied to the diode in its reverse biased condition, without causing breakdown.
Fig 4 : Presents a detailed design circuit of the proposed system
In the fig 4 of the circuit diagram of proposed system, there are two-part transmitter and receiver in which the transmitter place in the road sign which supported by the resistor when the amount of current is too high. And receiver place on the vehicle to receive the signal when the vehicles
approach at restricted areas like school, hospital and so on. So, this receiver transmits the signal to the microcontroller process it and allow the motor to decelerate when the speed is high.
2.7. Parts of circuit design
i. The power supply to the circuit
ii. Control system like microcontroller
iii. The Sensor used and location to be place
2.8. Power supply design
The power supply is a system used to transmit the power into the circuit in order the circuit operates the work properly. The power supply consists four components like Regulator, Transformer, Bridge or Diodes and capacitor. The regulator to be used decides to have 12V for primary and 240V for secondary coil.
In this system, there are two amount of voltage that will need for operation to take place.
i. 5V dc power supply for the microcontroller and sensor. In which 240V ac convert to 5V dc using the step-down transformer that will reduce the voltage.
ii. 12V dc power supply for motor driver used to driver a motor for high speed in the system. It easy way to regulate this voltage by using a7805 regulator whose output is 5V and 7812 regulator whose output is 12V
2.9. Control system
The control system includes the microcontroller, LCD display, motor driver and etc. This used to control the system operation in circuit. The type of microcontroller used is Arduino AT mega2560, It has 54 digital input/output pins, 16 analog inputs, 4 hardware serial ports, a 16 MHz It contains everything needed to support the microcontroller control the system operation in circuit.
Fig 5: Present the Arduino type of microcontroller
2.10. The sensor used and selection to be place
The sensor to be used is IR receiver sensor and IR transmitter sensor; in which receiver sensor place at the vehicle to give driver information concern the speed of vehicle at speed limiter areas. And IR transmitter place at road sign to transmit the signal to the driver for the system to take place.
The operating Voltage of this sensor is 3.0V – 5.0V and Current Consumption: at 3.3V: ~23 mA,at 5.0V: ~43 mA
2.11. Construction
This involved the physical connection of the components on the printed circuit board (PCB) after designing of the circuit, in this stage the construction of prototype is required for fulfillment of the project.
2.12. Simulation
The simulation is the imitation of the operation of a real-world process or system. The purpose of making circuit simulation is to check the performance of the designed circuit before the physical implementation of the prototype. The simulation will do in proteus 8 professional.
Different parts of this system after design were simulated in order to observe results of each part before implementing the complete circuit. The simulation of the circuit and the analysis of the result have been done in this part of the project and the available software used to fulfill the requirements.
2.13. Implementation and testing
The results obtained from the simulation compared with the result obtained in this part, in which the prototype realized from the circuit diagram and have been implemented on the PCB board the corrective procedures will be taken if the results will not meet the project requirements. However, if the results obtained will be correct then the circuit will further be taken to the test stage.
H. RESULTS AND DISCUSSION
Scope for the future, this method works very well to reduce excessive speeding and unintentional collisions in limited areas. Current technologies lack a vehicle's autonomous speed limit to prevent collisions. Therefore, more investigation and improvement of the autonomous vehicle speed control system will enable us to incorporate it into automobiles for increased roadside pedestrian, passenger, and other user safety.
I. CONCLUSION
The development of an automatic vehicle over-speed controlling system for restricted zones addresses a critical issue in road safety. By leveraging IR technology and microcontroller units, this project effectively monitors and regulates vehicle speeds in areas such as school zones and hospital areas where safety is paramount.
The system not only automates speed control but also enhances driver awareness and compliance with speed limits. This proactive approach has the potential to significantly reduce the frequency and severity of accidents caused by over-speeding, ultimately contributing to a safer driving environment for all road users.
The successful implementation of this technology suggests that further research and development could lead to broader applications in various traffic management systems. As autonomous driving technologies continue to evolve, integrating such systems can enhance safety measures and pave the way for smarter transportation solutions.
J. ACKNOWLEDGEMENTS
I, would like to thank my guide Dr.Ir. Ahmad Indra Siswantara for his continuous support and guidance. Because of his guidance, we completed our project successfully. I am extremely thankful to University of Indonesia for the support and encouragement.
K. REFFERENCES
Amarnaryan, S. C. M. C. K. A. and N. S. (2016). Automatic Over Speed Controlling of Vehicle. International Journal of Combined Research Development, 5(5), 706–709.
Bannatyne, R., & Viot, G. (1997). Introduction to microcontrollers. Wescon Conference Record, 564–574. https://doi.org/10.1201/9781420077681.ch1
Chidiobi, E., Obinna, M., & Okorie, E. E. (2022). Development On Automatic Vehicle Speed Control Using Radio Frequency Technology. 33(1), 503–513.
Hafsa, U., & Arifin, F. (2022). Design and Implementation of an Automatic Speed Control System of Vehicles for Avoiding Road Accidents in Bangladesh. Journal of Physics: Conference Series, 2312(1). https://doi.org/10.1088/1742-6596/2312/1/012006
Jiang, S., Smith, M. H., & Kitchen, J. (2009). Optimization of PID control for engine electronic throttle system using iterative feedback tuning. SAE Technical Papers, 4970.
https://doi.org/10.4271/2009-01-0370 Kasap, A. (2022). Autonomous Vehicles: Tracing the Locus of Regulation and Liability. Edward Elgar Publishing.
Kewate, S. R., Karmare, S. V, Sayankar, N., & Gavhale, S. (2014). Automatic Speed Control System by the Color Sensor for Automobiles–An Innovative Model Based Approach. International Journal of Advanced Mechanical Engineering, 4(2), 223–230.
Ng, I., & Guan, H. (2009). Electronic Throttle Control by.
Sai, C., Reddy, K., Reddy, S. A., Reddy, M. N., & Rajesh, A. (2022). Automatic Speed Control of Vechiles in Restricted Areas Using Ir and Gsm. International Research Journal of Modernization in Engineering Technology and Science Www.Irjmets.Com @International Research Journal of Modernization in Engineering, 5487(06), 2582–5208. www.irjmets.com
Sathiskumar, S., Navean, G. V., Hari Prakash, R., & Vishnu Praveen, S. (2020a). Automatic vehicle speed control system in a restricted zone. International Journal of Scientific and Technology Research, 9(2), 2207–2210.
Sathiskumar, S., Navean, G. V, Hari Prakash, R., & Vishnu Praveen, S. (2020b). Automatic vehicle speed control system in a restricted zone. International Journal Of Scientific & Technology Research, 9(02).
Technology, H. (2015). Liquid Crystal Display-LCD Technology and Application. http://www.handsontec.com
Zribi, M., & Chiasson, J. (1991). Position Control of a PM Stepper Motor by Exact Linearization. IEEE Transactions on Automatic Control, 36(5), 620–625. https://doi.org/10.1109/9.7636
L. APPENDICES
Table