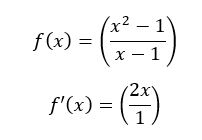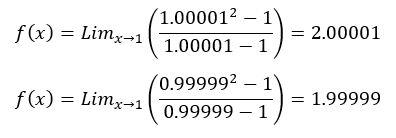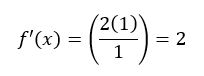Romy Rizky

Introduction

Nama : Romy Rizky

NPM  : 1806155365

Jurusan : Teknik Mesin

Peminatan : Konversi Energi

Resume Komputasi Teknik

Resume kelas Komputasi Teknik tanggal 4 Februari 2019:

Beberapa kasus khusunya di bidang rekayasa atau engineering sering didapati suatu persoalan yang dapat didapatkan dengan perhitungan matematis, analitik dan numerik. Namun ketika dihadapi dengan keterlibatan banyak parameter membuat persoalan tersebut sulit di selesaikan dengan cara analitik sehingga dibutuhkan perhitungan dengan metode numeric untuk menyelesaikannya. Untuk memudahkan perhitungan secara numeric bantuan komputer sangat di perlukan untuk memudahkan perhitungan secara berulang atau iterasi dan bisa di sebut juga komputasi. Mengetahui tentang komputasi menjadi penting, namun prinsip dasarnya adalah bukan untuk mempelajari software, tetapi lebih pada mengenal fenomena pesoalan dan membuat permodelan dengan menggunakan software sesuai dengan kebutuhan. Dalam mempelajari komputasi teknik diantara memahami konsep algoritma, flow chart, model iterasi dan sebagainya sehingga dapat diaplikasikan. Dalam kuliah komputasi teknik diharapkan mahasiswa mampu mengaplikasikan dalam kehidupan sebagai seorang pembelajar. Namun tidak hanya pada persoalan matematis dan keteknikan saja, diharapkan juga mampu memahami hal-hal positif untuk dapat menjadi pribadi yang lebih baik. Berpikir secara logis dengan mengedepankan akal disetiap menyelesaikan permasalah. Misalnya dalam penyelesaian soal (x^2-9)/(x-3)=⋯? Jika Penyelesaian persoalan tersebut dengan menggunakan subtitisi langsung x=3, akan menghasilkan nilai 0/0, maka persoalan tersebut diselesaikan dengan menggunakan konsep limit metode pemfaktoran sehingga penyelesaiannya menjadi (x^2-9)/(x-3)=lim┬(x=3)⁡〖((x+3)(x-3))/((x-3))〗=lim┬(x=3)⁡〖(x+3)=6〗.

5. Bayangan tentang ilmu Koputasi Teknik yaitu, kita harus mengetahui konsep modelling ata computer modelling dengan parameter sebagai berikut:

- Software : Aplikasi yang kita gunakan

- Hardware : Perangkat fisik yang kita gunakan

- Brainware : Kita sebagai user

Jelaskan konsep "Infinite"

Jika kita berbicara tentang definisi, Definisi dari simbol tak hingga (Infinity) adalah sebuah konsep abstrak yang menggambarkan sesuatu yang tanpa batas dan relevan dalam sejumlah bidang, terutama matematika dan fisika.Tak hingga (Infinity) itu dalam daftar simbol matematika yang telah diorganisir menurut jenis simbolnya termasuk ke dalam daftar simbol bukan huruf yang lain dan merupakan kategori bilangan.Namun, ada beberapa orang yang berpendapat bahwa tak hingga bukan benar-benar bilangan. Tak berlaku seperti bilangan yang biasa kita gunakan. Bilangan yang kita gunakan seluruhnya memiliki akhir, tetapi tak hingga tidak memilikinya. Beberapa orang juga ada yang berpendapat bahwa tak hingga ialah tiap bilangan (kecuali 0) yang dibagi oleh 0 sehingga bernilai tak hingga.

Bagaimana anda menjelaskan secara rasional atas pertanyaan berapa nilai (x2-1)/(x-1) jika x=1 ?

Dimana nilai dari x = 1 Jika kita langsung memasukkan angka tersebut pada persamaan yang digunakan, maka hasil yang diperoleh adalah infinite atau tak terhingga karena 0 dibagi dengan 0 adalah tak terhingga. Namun kita dapat menyelesaikan persamaan tersebut dengan beberapa cara matematis. Menurut saya terdapat 3 cara untuk mengatasi persamaan tersebut, yaitu:

1. Menggunakan Limit Menggunakan Limit pada persamaan ini didasari pada nilai x=1 memiliki digit dibelakangnya sehingga hasil yang dihasilkan nantinya tidak seutuhnya adalah nol. Dimana dengan menggunakan limit, nilai yang digunakan adalah mendekati nilai 1. Sebagai contoh: Dimana, x = 1.00001 x = 0.99999

Sehingga dihasilkan:

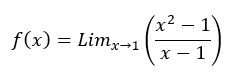
2. Menyederhanakan Bentuk persamaan Menyederhanakan persamaan yang akan digunakan terlebih dahulu kemudian barulah dapat dimasukkan angkanya. Sehingga hasil yang diperoleh nantinya tidak akan menghasilkan angka tak terhingga.

Sehingga dihasilkan:

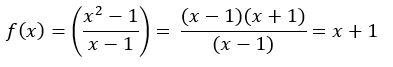
3. Menurunkan Persamaan Menurunkan persamaan yang digunakan terlebih dahulu sebelum melakukan subtitusi nilai 1

Sehingga dihasilkan:

KOMPUTASI TEKNIK PR1

[1]

KOMPUTASI TEKNIK PR2

[2]

KOMPUTASI TEKNIK PR3

[3]

KOMPUTASI TEKNIK QUIZ1

[4]

KOMPUTASI TEKNIK PR4

[5]

KOMPUTASI TEKNIK PR5

[6]

KOMPUTASI TEKNIK PR6

[7]

KOMPUTASI TEKNIK TUGAS UTS

[8]

KOMPUTASI TEKNIK PR7

[9]

KOMPUTASI TEKNIK PR8

[10]

KOMPUTASI TEKNIK PROGRES1 TUGAS BESAR

[11] [12]