Revaldy Putra Agatha

1 Biodata Diri
2 Metode Numerik
3 Review Materi Sebelum UTS
4 REVIEW PERTEMUAN
5 Pertemuan Minggu Ke-1 ( Rabu, 11 November 2020 )
- 5.1 Tugas Minggu Pertama
6 Pertemuan Minggu Ke-2 ( Rabu, 18 November 2020 )
- 6.1 Tugas Minggu Ke-2
7 Pertemuan Minggu Ke-3 ( Rabu, 25 November 2020 )
8 Senin, 14-12-2020
9 Rabu, 16-12-2020
10 Tugas Besar Metode Numerik
11 UAS

Biodata Diri

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Nama : Revaldy Putra Agatha

NPM : 1906379125

Prodi : S1 Teknik Mesin Reguler

TTL : Surabaya, 27 Juli 2000

Angkatan : 2019

Alasan saya masuk ke program studi teknik mesin adalah karena saya waktu SMA sangat suka dengan pelajaran fisika dan matematika sehingga saya berkeinginan untuk mempelajarinya lebih dalam lagi terutama penerapannya langsung dalam kehidupan. Nantinya dengan saya menempuh bidang studi teknik mesin ini saya berharap saya dapat membantu orang lain dalam memecahkan suatu masalah mengenai mesin maupun tentang keteknikan karena dalam suatu hadits Rasulullah SAW pernah bersabda : خَيْرُ الناسِ أَنفَعُهُم لِلنَّاسِ “Sebaik-baik manusia adalah yang paling bermanfaat bagi orang lain.” (Hadits Riwayat ath-Thabrani, Al-Mu’jam al-Ausath, juz VII, hal. 58, dari Jabir bin Abdullah r.a.. Dishahihkan Muhammad Nashiruddin al-Albani dalam kitab: As-Silsilah Ash-Shahîhah).

Metode Numerik

Metode Numerik adalah teknik penyelesaian permasalahn yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis yang tidak dapat diselesaikan menggunakan metode analitik. Jikapun terdapat penyelesaiannya secara analitik, proses penyelesaiaannya sering kali cukup rumit dan memakan banyak waktu sehingga tidak efisien.

Review Materi Sebelum UTS

Sebelum UTS sampai UTS berlangsung kelas Metode Numerik 2 diampu oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Beberapa materi yang telah dibahas antara lain :

Pseudocode

Deret Taylor dan Mclaurin

Penyelesaian suatu sistem persamaan dengan menggunakan beberapa metode :

 - Metode Newton Rhapson
 - Metode Sekan
 - Metode Biseksi

Interpolasi

Turunan Numerik

Regresi Linear

Sedangkan untuk materi sesudah UTS sampai UAS berlangsung kelas ini akan diampu oleh Bapak Dr. Ir. Ahmad Indra Siswantara.

REVIEW PERTEMUAN

Pertemuan Minggu Ke-1 ( Rabu, 11 November 2020 )

Pada minggu ini saya dijelaskan beberapa tujuan dalam kita mempelajari metode numerik, antara lain :

1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik. Contoh : Persamaan aljabar, algoritma, pencocokan kurva, persamaan diferensial parsial, dll.

2. Mengerti aplikasi dari belajar metode numerik

3. Mampu menerapkan metode numerik dalam persoalan keteknikan

4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab

Selain itu juga pada minggu ini juga mencoba mensimulasikan perangkat lunak openmodellica dalam kegunaannya untuk menyelesaikan suatu sistem persamaan.

Tugas Minggu Pertama

Pada tugas minggu pertama saya diberi tugas untuk mempelajari open modellica. Dalam mempelajari open modellica saya menggunakan referensi dari video berikut :

https://www.youtube.com/watch?v=m0Ahs8fEN28&ab_channel=NSTUFACE

https://www.youtube.com/watch?v=GhtBMIlO70w&ab_channel=Processdynamicsandcontrol

Berikut adalah link dari tugas saya yang mengangkat permasalahan mengenai penyelesaian dari sistem persamaan linear:

Pertemuan Minggu Ke-2 ( Rabu, 18 November 2020 )

Pada pertemuan minggu ke-2 ini dimulai dengan mempresentasikan tugas yang diberikan di minggu kemarin oleh beberapa mahasiswa. disela-sela presentasi kami juga membahas mengenai fitur class function dan dijelaskan alasan mengapa menggunakan aplikasi open modellica sebagai media untuk mempelajari metode numerik. Jawaban dari pertanyaan tersebut adalah karena aplikasi open modellica lebih mudah untuk digunakan di berbagai perangkat ( tidak harus perangkat dengan spesifikasi tinggi ) dan yang paling penting lagi murah.

Tugas Minggu Ke-2

Pada tugas minggu kedua ditugaskan untuk membuat suatu sistem untuk menyelesaikan persamaan aljabar simultan. Berikut link video dari tugas saya :

Pertemuan Minggu Ke-3 ( Rabu, 25 November 2020 )

Pada pertemuan minggu ke-3 ini dimulai dengan review tugas yang telah diberikan di minggu kemarin oleh beberapa mahasiswa. Selanjutnya Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada Computation Fluid Dynamics (CFD), lalu Finite Element Analysis, dan Metode Stokastik. CFD dan FEA berbasis ilmu fisika, kemudian metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik :

Riset masalah tekniknya terlebih dahulu
Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya)
Membuat model matematika
Membuat model numerik
Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan output yang diinginkan

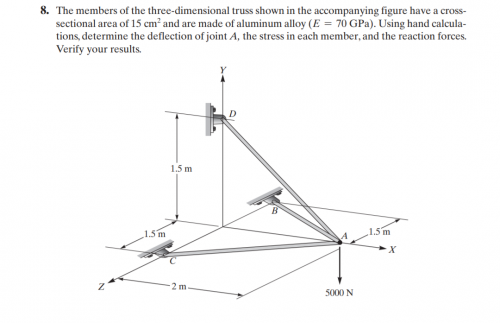
Agar Kami bisa lebih paham tentang dasar-dasar metode numerik, Pak Dai menyuruh Kami untuk mencoba membuat fungsi untuk menyelesaikan Persamaan 9.12 di buku Numerical Methods for Engineers 7th Edition oleh Chapra dengan cara apapun (misalnya eliminasi gauss). Kedua, Kami disuru latihan menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan cara pseudocode 9.4 untuk menjawab soal 9.5 yang ada di buku yang sama juga. Latihan yang kedua ini dimaksudkan agar Kami paham dalam penggunaan array dalam penggunaan OpenModelica, yang dimana array ini dapat memudahkan mengumpulkan himpunan penyelesaian.

Tugas Minggu Ke-3

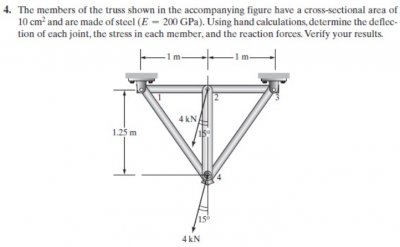
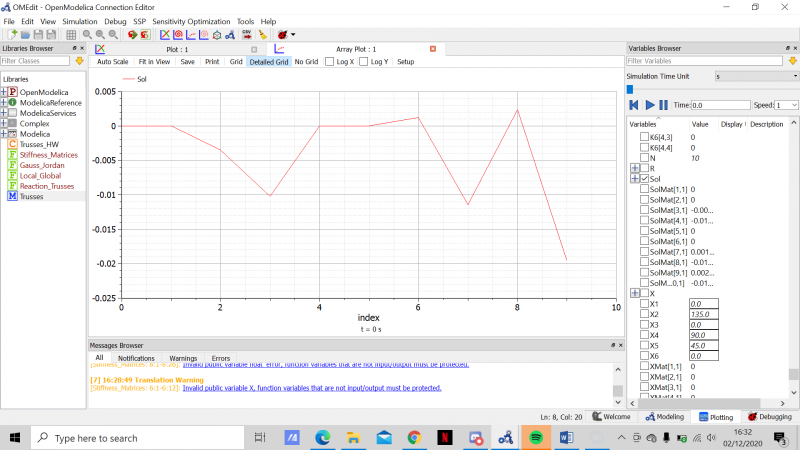
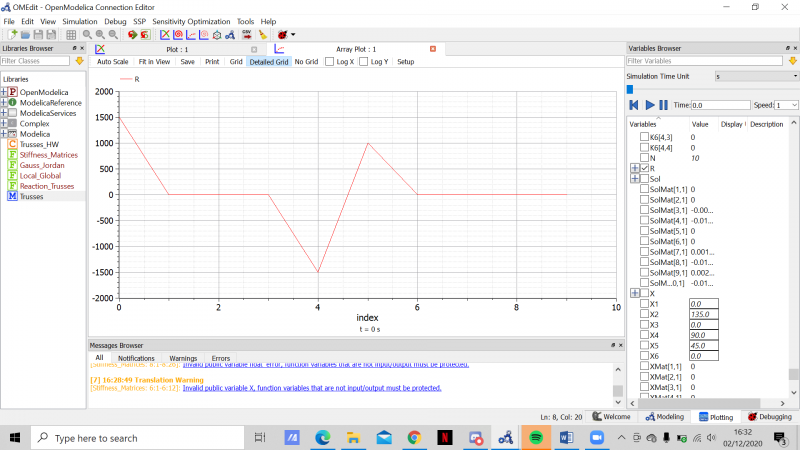
Kami diberi tugas oleh Pak Dai untuk membuat program sederhana atau penyelesaian dari soal statika struktur dibawah ini dengan OpenModelica

Trusses

class Trusses_HW

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_HW;

Fungsi Panggil

Matrice Transformation

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Reaction Matrice Equation

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;

Gauss Jordan

function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10;

algorithm X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop

 if abs(X[i]) <= float_error then
   X[i] := 0;
 end if;

end for;

end Gauss_Jordan;

Hasil Perhitungan

Quiz Flowchart dan Diagram Class

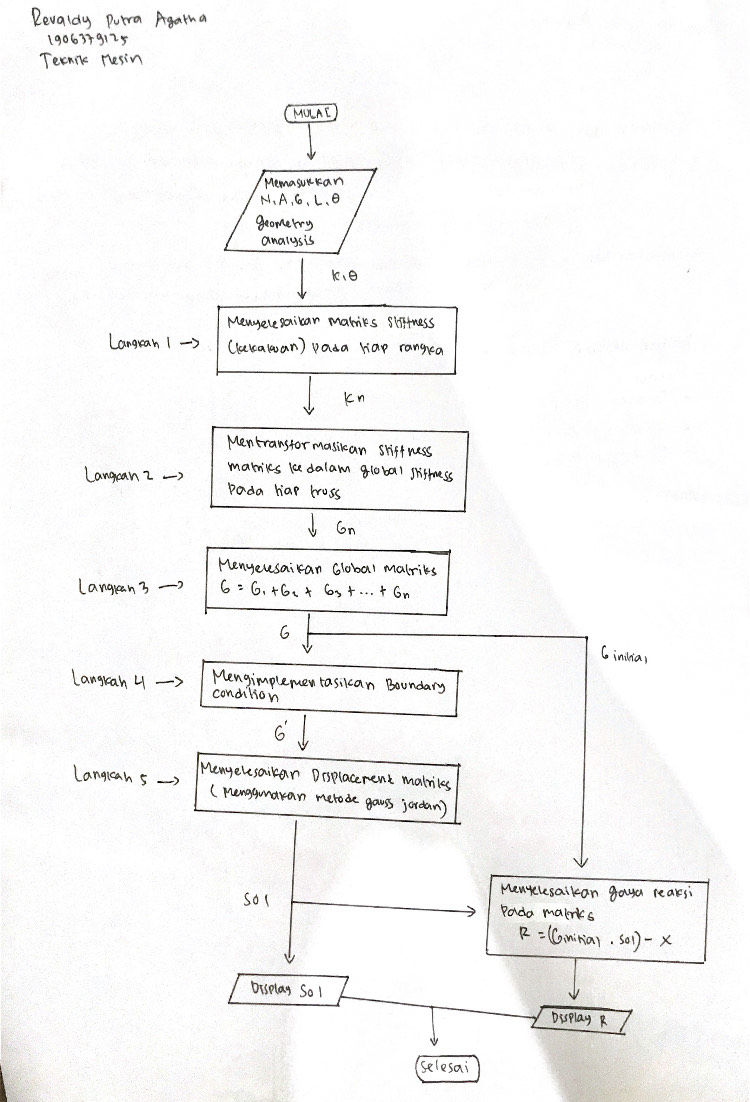
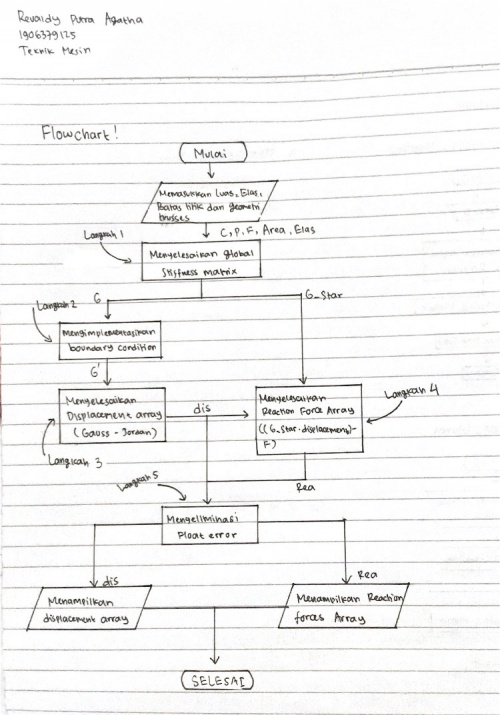
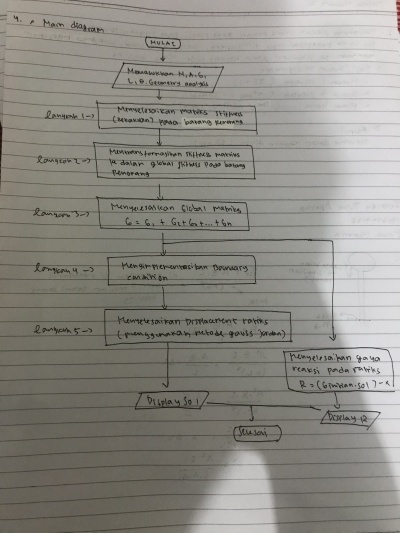
Dalam quiz kali ini diberi tugas untuk membuat suatu flowchart yang menggambarkan proses dalam memperoleh penmyelesaian dari kasus trusses

flowchart

Tugas 4

Membuat flowchart dan open modellica dari soal nomor 8

Trusses3D

class Trusses3D

//define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Area=0.0015; //Area
parameter Real Elas=70e9; //Elasticity

//define connection
parameter Integer C[Trusses,2]=[1,2;
                                1,3;
                                1,4];
                              
//define coordinates (please put orderly)
parameter Real P[Points,3]=[2,0,0;
                            0,0,1.5;
                            0,0,-1.5;
                            0,1.5,0]; 

//define external force (please put orderly)
parameter Real F[Points*3]={0,-5000,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0}; 

//define boundary
parameter Integer b[:]={2,3,4};

//solution
Real displacement[N], reaction[N];

protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, E, X[3,3];

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
   q1[j]:=P[C[i,1],j];
   q2[j]:=P[C[i,2],j];
 end for;
       
       //Solving Constant
       L:=Modelica.Math.Vectors.length(q2-q1);
       E:=Area*Elas/L;

       //Solving Matrix
       cx:=(q2[1]-q1[1])/L;
       cy:=(q2[2]-q1[2])/L;
       cz:=(q2[3]-q1[3])/L; 
       X:=E*[cx^2,cx*cy,cx*cz;
             cy*cx,cy^2,cy*cz;
             cz*cx,cz*cy,cz^2];

       //Transforming to global matrix
       g:=zeros(N,N); 
       for m,n in 1:3 loop
         g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
         g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
         g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
         g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
       end for;  
 
 G_star:=G+g;
 G:=G_star;
end for;

//Implementing boundary
for i in boundary loop
 for j in 1:N loop
   G[i,j]:=id[i,j];
 end for;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

end Trusses3D;

Video Penjelasan

Senin, 14-12-2020

Kelas pengganti Metode Numerik pada Rabu 9 Desember 2020, Pada kelas ini kami juga diajarkan kembali tentang sistem trusses menggunakan software open modelica. Pak Dai sebagai dosen metnum juga mengajarkan tentang pelajaran-pelajaran hidup. Pada pertemuan kali ini kami diajarkan untuk melakukan muhasabah terhadap penilaian diri sendiri mengenai materi Metode Numerik yang sudah diberikan oleh Pak Dai. Setelah itu kami juga diajarkan mengenai sistem trusses dengan metode belajar kelompok bersama kelas Metnum 2 dan Metnum 3.

Rabu, 16-12-2020

Pada pertemuan Metnum Rabu, 16 Desesmber 2020 kami diajarkan tentang optimasi menggunakan Open Modelica. Optimasi merupakan sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada pertemuan ini Asisten Dosen Metode Numerik yaitu Bu Chandra memberikan tutorial atau mengajarkan cara untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu grafik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan hingga melakukan optimasi grafik tanpa sebuah konstrain.

Berikut merupakan coding open modelica yang diajarkan oleh Bu Chandra:

Fungsi panggil

function f_obj3
import Modelica.Math;
input Real x;
output Real y;
algorithm
y:= 2*Math.sin(x)-x^2/10;
end f_obj3;

Setelah itu dibuat lah model optimasi sistem bracketnya:

model bracket_optimation3
parameter Integer n=8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real d;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
algorithm
xup :=4;
xlow:=0;
for i in (1:n) loop
  d:= (5^(1/2)-1)/2*(xup-xlow);
  x1[i]:= xlow+d;
  x2[i]:= xup-d;
  f1[i]:= f_obj3(x1[i]);
  f2[i]:= f_obj3(x2[i]);
  if f1[i]>f2[i] then
  xup:= xup;
  xlow:= x2[i];
  xopt:= xup;
  yopt:= f1[i];
  else
  xlow:= xlow;
  xup:= x1[i];
  xopt:= xup;
  end if;
  end for;
end bracket_optimation3;

Tugas Besar Metode Numerik

Soal Tugas Besar Metode Numerik

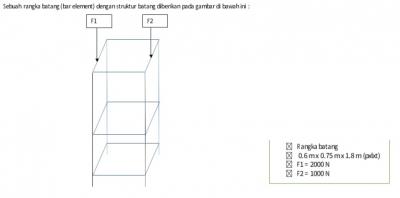
Tugas besar Metode Numerik yaitu mengoptimasi harga pembuatan rangka truss sederhana dengan memvariasi dimensi dan elastisitas material. Variabel-variabel penting dalam menentukan cost terendah:

Jenis material
Harga material
Luas penampang truss
Mencari nilai displacement, reaction, dan streess

Lalu melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode Numerik dan aplikasi Open Modelica.

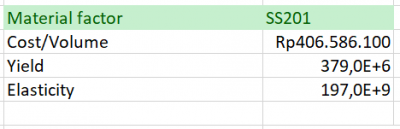
Langkah Pertama yaitu menentukan material yang ingin digunakan, saya memilih stainless steel 201 dengan Mechanical Properties yaitu: Yield=379 MPa, Elasticity= 197 GPa, dan luas truss 184 mm^2 (L profile 25x25mm thickness 4mm).

Lalu melakukan coding di OpenModelica dengan program sebagai berikut:

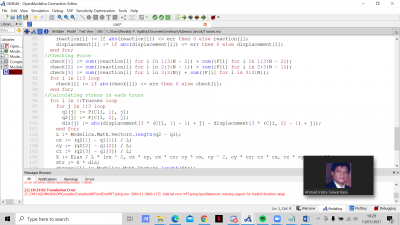
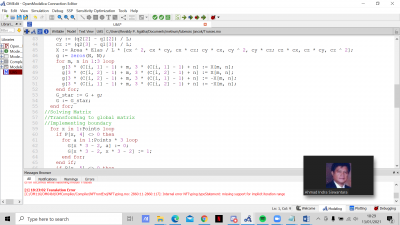
model Tugas_3D_Besar_Safety

/define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=379e6; //Yield Strength (Pa)
parameter Real Area=0.000184;   //Area L Profile (Dimension=25x25mm, Thickness=4mm) (m2)
parameter Real Elas=197e9;     //Elasticity SS 201  (Pa)

//define connection
parameter Integer C[:,2]=[1,5; 
                          2,6;
                          3,7;
                          4,8;
                          5,6;  //1st floor
                          6,7;  //1st floor
                          7,8;  //1st floor
                          5,8;  //1st floor
                          5,9;
                         6,10;
                         7,11;
                         8,12;
                         9,10; //2nd floor
                         10,11;//2nd floor 
                         11,12;//2nd floor
                          9,12; //2nd floor
                          9,13;
                         10,14;
                         11,15;
                         12,16;
                         13,14;//3rd floor
                         14,15;//3rd floor
                         15,16;//3rd floor
                        13,16];//3rd floor
                                                              
//define coordinates (please put orderly)
parameter Real P[:,6]=[-0.6,0,0,1,1,1;//1
                         0,0,0,1,1,1;//2
                         0,0.75,0,1,1,1;//3
                      -0.6,0.75,0,1,1,1;//4
                      -0.6,0,0.6,0,0,0;//5
                         0,0,0.6,0,0,0;//6
                         0,0.75,0.6,0,0,0;//7
                      -0.6,0.75,0.6,0,0,0;//8
                      -0.6,0,1.2,0,0,0;//9
                         0,0,1.2,0,0,0;//10  
                         0,0.75,1.2,0,0,0;//11
                      -0.6,0.75,1.2,0,0,0;//12
                      -0.6,0,1.8,0,0,0;//13
                         0,0,1.8,0,0,0;//14
                         0,0.75,1.8,0,0,0;//15
                      -0.6,0.75,1.8,0,0,0];//16
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,-500, 
                            0,0,-1000, 
                            0,0,-1000, 
                            0,0,-500}; 

//solution
Real displacement[N], reaction[N];
Real check[3];

Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
 
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2];

   //Transforming to global matrix
   g:=zeros(N,N); 
   for m,n in 1:3 loop
     g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
     g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
     g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
   end for;  

 G_star:=G+g;
 G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
 if P[x,4] <> 0 then
   for a in 1:Points*3 loop
     G[(x*3)-2,a]:=0;
     G[(x*3)-2,(x*3)-2]:=1;
   end for;
 end if;
 if P[x,5] <> 0 then
   for a in 1:Points*3 loop
     G[(x*3)-1,a]:=0;
     G[(x*3)-1,(x*3)-1]:=1;
   end for;
 end if;
 if P[x,6] <> 0 then
   for a in 1:Points*3 loop
     G[x*3,a]:=0;
     G[x*3,x*3]:=1;
   end for;
 end if;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
  
for i in 1:3 loop
 check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;

//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];
   
   Str:=(X*dis);
   stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;

//Safety factor
for i in 1:Trusses loop
 if stress1[i]>0 then
   safety[i]:=Yield/stress1[i];
 else
   safety[i]:=0;
 end if; 
end for;

end Trusses_3D_Tugas_Besar_Safety;

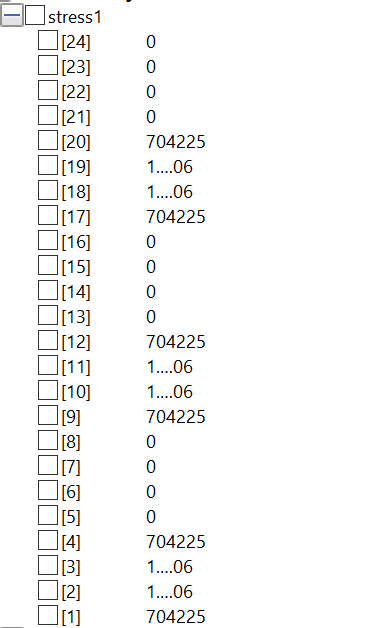
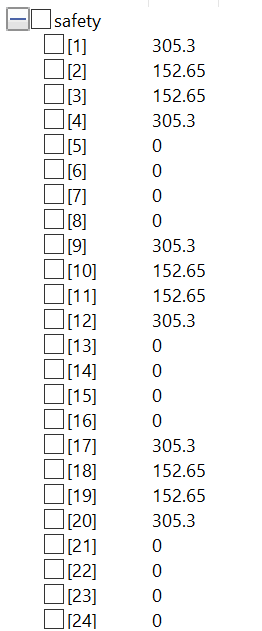
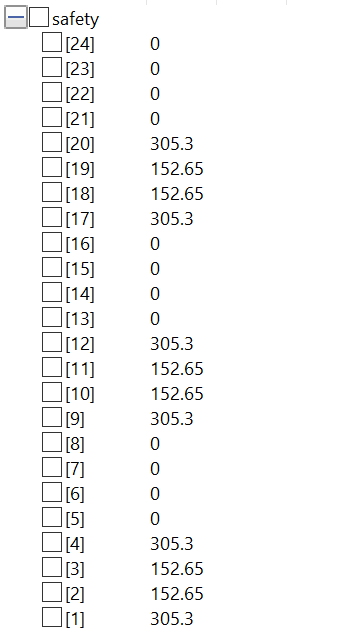
Berikut ini merupakan hasil dari perhitungan menggunakan program tersebut :

Displacement

Stress

Safety Factor

Reaction

Setelah ditemukan data-data diatas dilakukan optimasi dengan menggunakan dua metode yaitu : 1. Material tetap dan Luas penampang berubah-ubah

  Material yang digunakan tetap menggunakan SS201

2. Luas Penampang tetap dan Material Berubah-ubah

  Luas yang digunakan tetap menggunakan luas penampang sebesar 184 mm^2

setiuap metode tersebut nantinya akan dihitung nilai total harga, safety factor, dan rasio. Kemudian dilakukan curve fitting dan melakukan optimasi.

1. Jenis Material Tetap

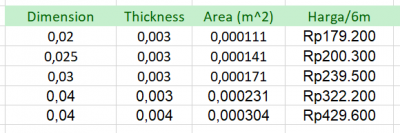
Setelah dilakukan perhitungan didapatkan data sebagai berikut :

Selanjutnya dilakukan optimasi dan didapatkan hasil sebagai berikut :

Dari hasil yang didapat , dapat disimpulkan bahwa dengan menggunkan material ss201 luas area yang optimum adalah dengan 303 mm^2.

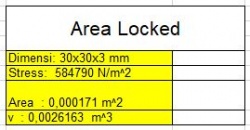
2.Untuk area penampang yang sama

Data yang dipakai adalah

Hasil perhitungan yang didapat adalah

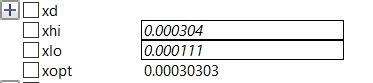
Kemudian kita gunakan open modelica untuk mengoptimasi data yang sudah didapat. pada kali ini saya menggunakan nilai minimum xlo=193e+11 dan nilai maksimum xhi= 200e+11. Maka didapatlah hasil optimasi seperti berikut:

Dari hasil yang didapat, dapat disimpulkan bahwa dengan luas area truss sebesar 171 mm^2 , material yang paling cocok untuk bahan dasar rangka adalah material stainless steel s201 dengan modulus elastisitas sebesar 1.93035x10^13 Pa

UAS

Revaldy Putra Agatha

1906379125

Metode Numerik 2

Program dalam open modellica :

model UAS_Rev
//define initial variable
parameter Integer Points = size(P, 1);
//Number of Points
parameter Integer Trusses = size(C, 1);
//Number of Trusses
parameter Real Yield = 305e6;
//Yield Strength (Pa)
parameter Real Area = 40;
//Area L Profile
parameter Real Elas = 70e9;
//Elasticity Al 6061 (Pa)
//define connection
parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4];
//define coordinates (please put orderly)
parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1
6.5, 6.5, 36.5, 1, 1, 1; //2
6.5, 6.5, 36.5, 1, 1, 1; //3
6.5, 6.5, 36.5, 1, 1, 1]; //4
//define external force (please put orderly)
parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N = 3 * Points;
Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3];
Real err = 10e-10, ers = 10e-4;
algorithm
//Creating Global Matrix
G := id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
g := zeros(N, N);
for m, n in 1:3 loop
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n];
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n];
end for;
G_star := G + g;
G := G_star;
end for;
//Solving Matrix
//Transforming to global matrix
//Implementing boundary
for x in 1:Points loop
if P[x, 4] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 2, a] := 0;
G[x * 3 - 2, x * 3 - 2] := 1;
end for;
end if;
if P[x, 5] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 1, a] := 0;
G[x * 3 - 1, x * 3 - 1] := 1;
end for;
end if;
if P[x, 6] <> 0 then
for a in 1:Points * 3 loop
G[x * 3, a] := 0;
G[x * 3, x * 3] := 1;
end for;
end if;
end for;
//Solving displacement
displacement := Modelica.Math.Matrices.solve(G, F);
//Solving reaction
reaction := G_star * displacement - F;
//Eliminating float error
for i in 1:N loop
reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i];
displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i];
end for;
//Checking Force
check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2});
check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1});
check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N});
for i in 1:3 loop
check[i] := if abs(check[i]) <= ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]);
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
Str := X * dis;
stress1[i] := Modelica.Math.Vectors.length(Str);
end for;
//Solving Matrix
//Safety factor
for i in 1:Trusses loop
if stress1[i] > 0 then
safety[i] := Yield / stress1[i];
else
safety[i] := 0;
end if;
end for;
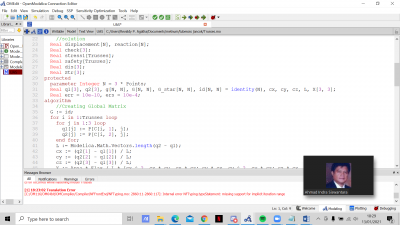
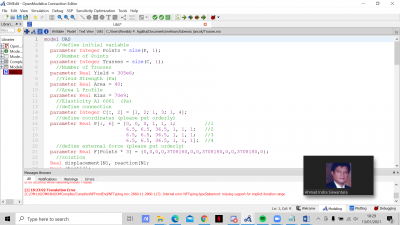
end UAS_Rev;