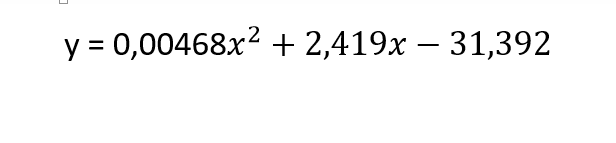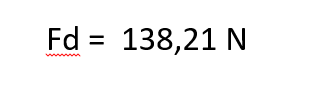Report Tugas Kelompok 9 : Metode Numerik 2019

From ccitonlinewiki
Jump to: navigation, search

Nama Kelompok:

Abraham thedorus, (1706036103)

Dimas fahrul rozi (1706986340)

Muhammad ichsan (1706036122)


Tugas 1

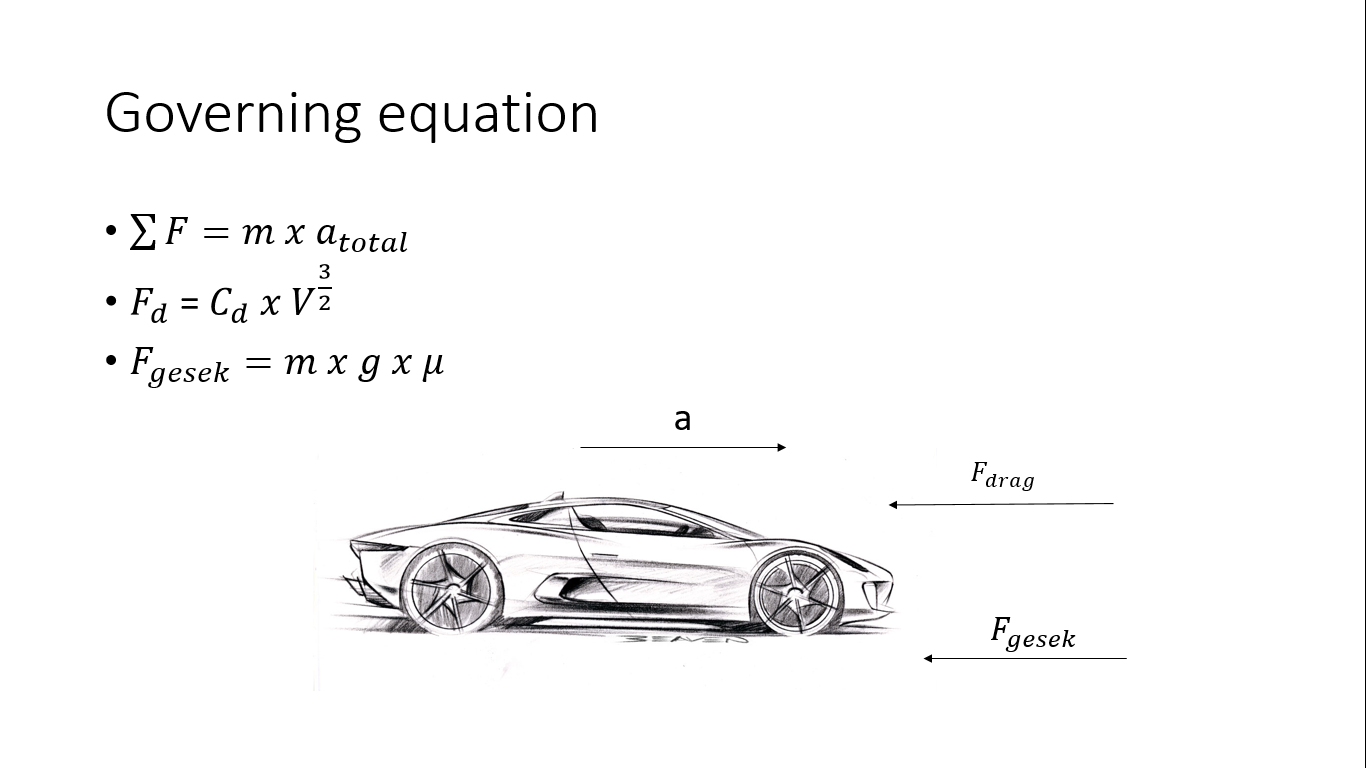
Dimana kita menggunakan aplikasi phyton untuk mencari waktu top speed. pada masalah yang ada pada governing equation. Kita juga dituntut untuk menggunakan methode kutta


Mobilmobil.png Mobil1mobil.png Mobil2mobil.png


Pseudocode memasukkan nilai variabel yang diperlukan

g= float(9.8) #gravitational_acceleration

cd=eval(input("drag coefficient: "))

myu= float(input("koefisien gesek dinamis: "))

v0=eval(input("initial velocity (m/s): "))

m=eval(input("mass (kg): "))

a=eval(input("acceleration (m/s^2): "))

vt=eval(input("top speed (m/s): "))

semua dibagi m

fgesek=g*myu

fdrag=(cd*vt**(3/2))/m

ft=a

atot=ft-fdrag-fgesek

t=(vt-v0)/atot

print("waktu mobil untuk mencapai top speed: ",t, "detik")

Kemudian

Penjelasan dari saya berupa video




Tugas 2

Drag force

(Gaya hambat)

Dalam dinamika fluida, gaya hambat (yang kadang-kadang disebut hambatan fluida atau seretan) adalah gaya yang menghambat pergerakan sebuah benda padat melalui sebuah fluida ( cairan atau gas). Bentuk gaya hambat yang paling umum tersusun dari sejumlah gaya gesek, yang bertindak sejajar dengan permukaan benda, plus gaya tekanan, yang bertindak dalam arah tegak lurus dengan permukaan benda. Bagi sebuah benda padat yang bergerak melalui sebuah fluida, gaya hambat merupakan komponen dari aerodinamika gaya resultan atau gaya dinamika fluida yang bekerja dalam arahnya pergerakan. Komponen tegak lurus terhadap arah pergerakan ini dianggap sebagai gaya angkat. Dengan begitu gaya hambat berlawanan dengan arah pergerakan benda, dan dalam sebuah kendaraan yang digerakkan mesin diatasi dengan gaya dorong.

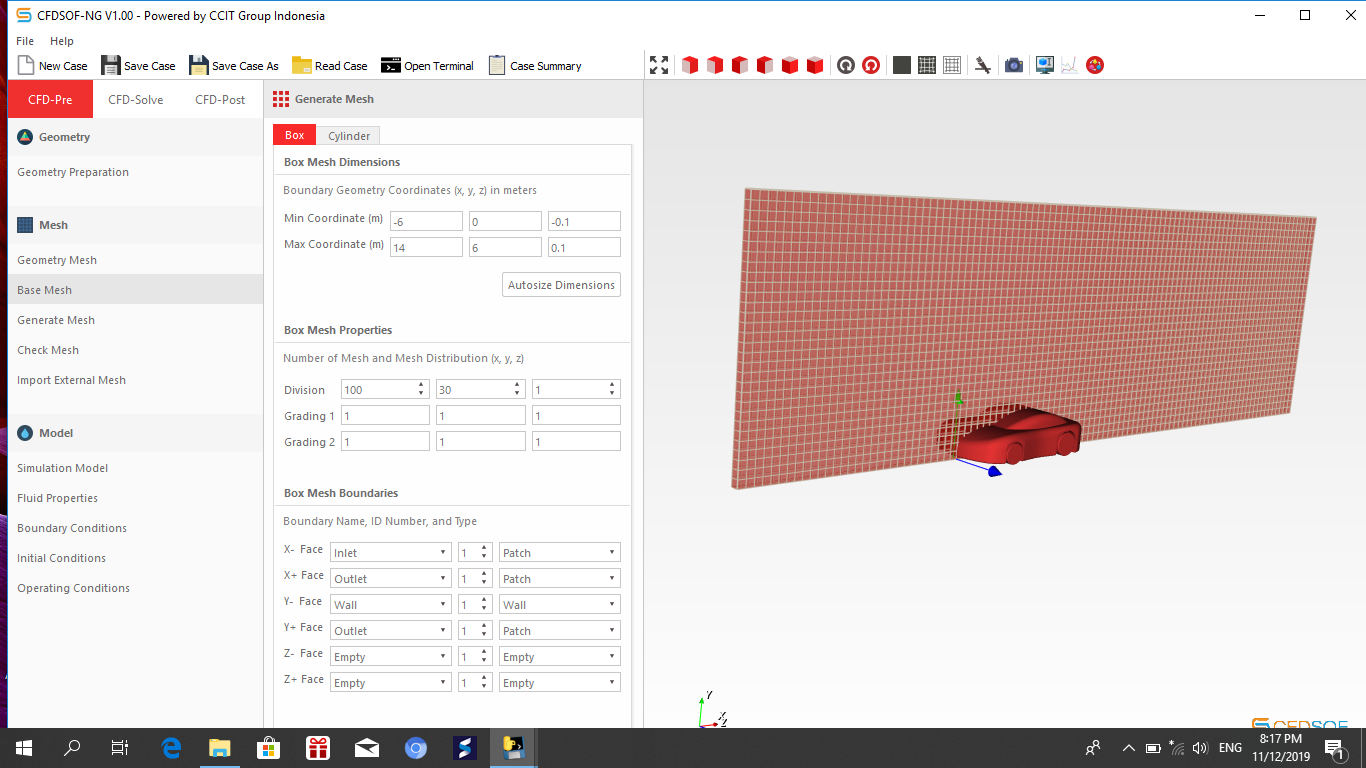
Parameter meshing

Parameter meshing yang kami gunakan pada CFDSOF:

Tugastugas11.png

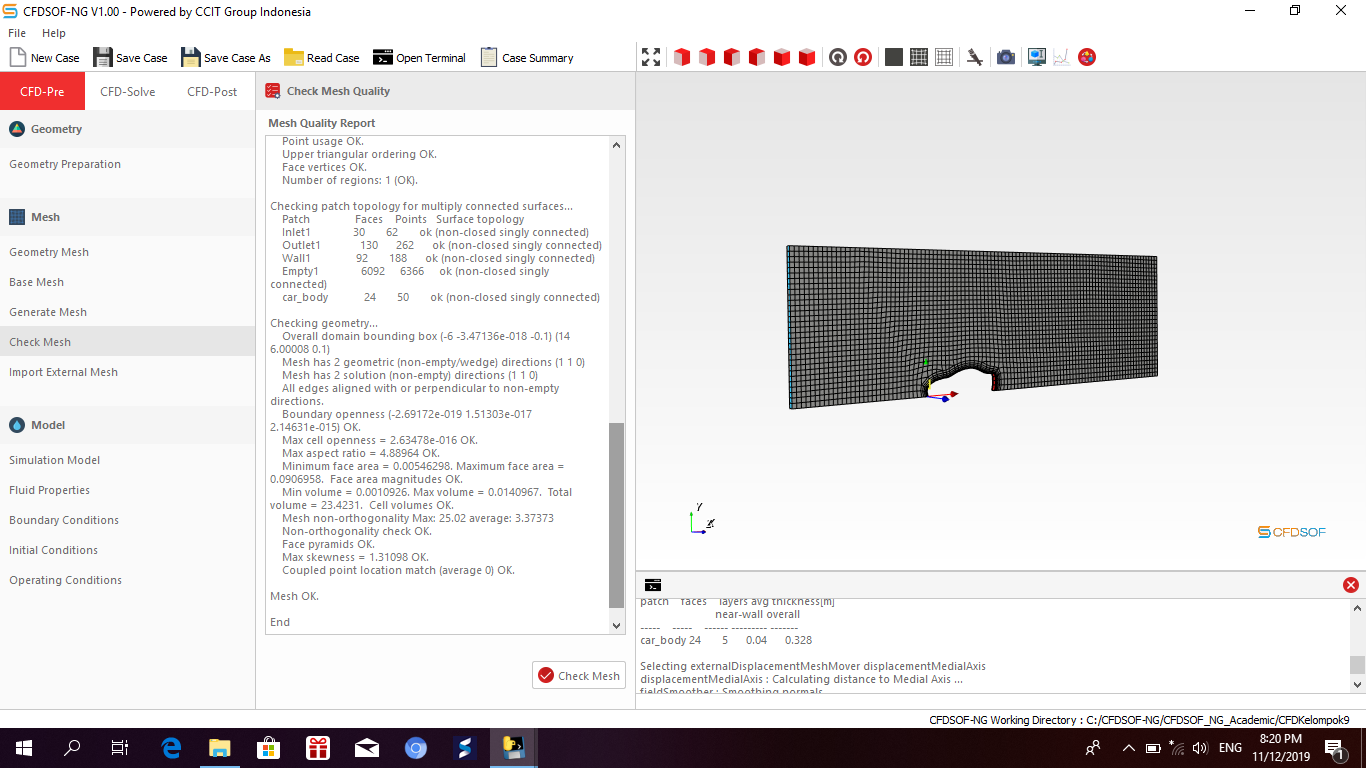
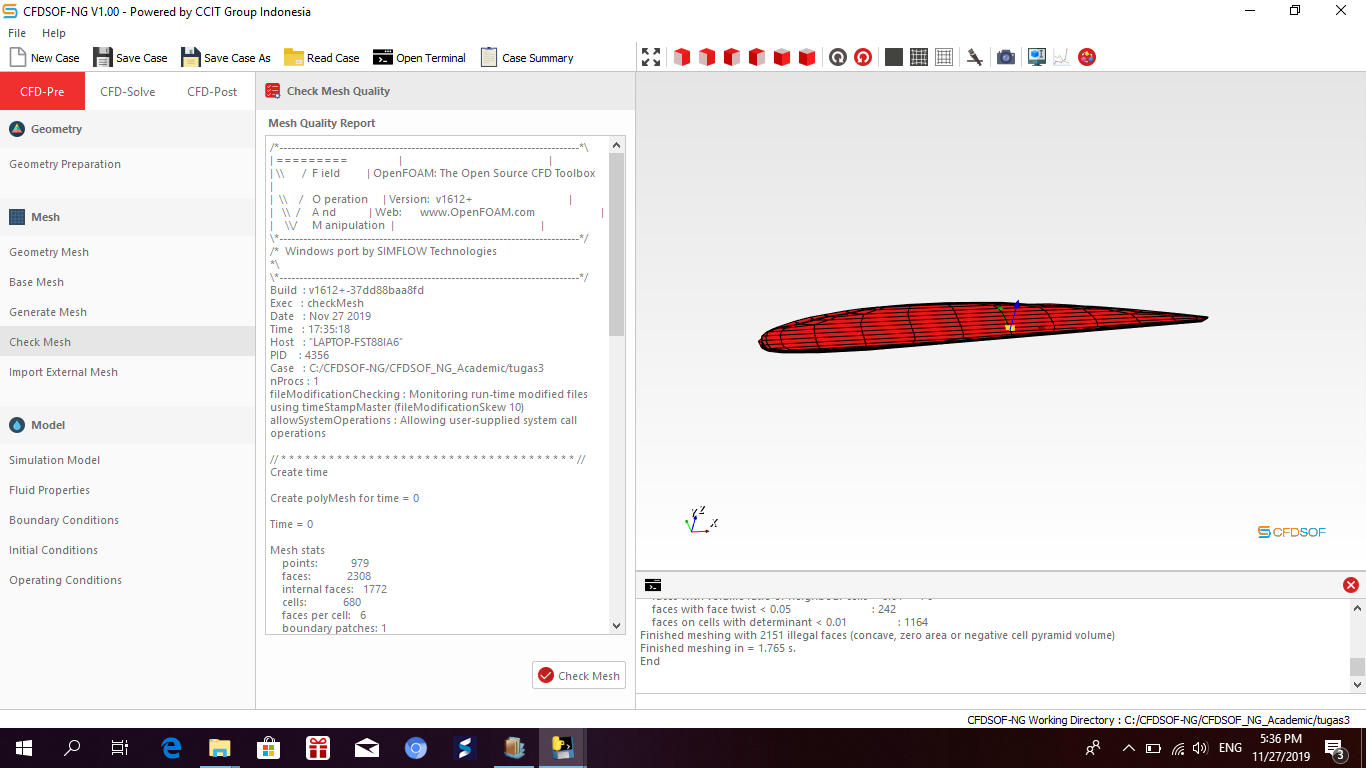
Check mesh quality

111111tugas.png

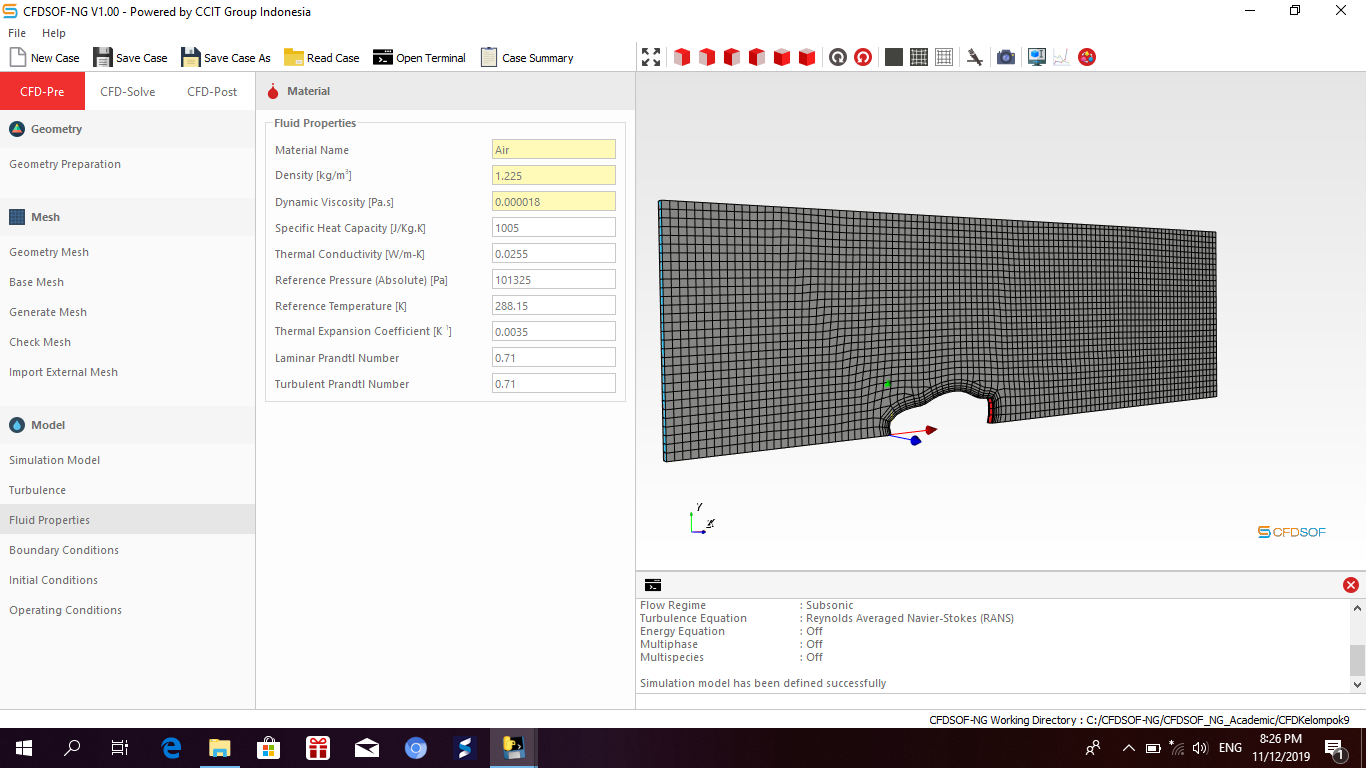
FLuida properties

123tug.png

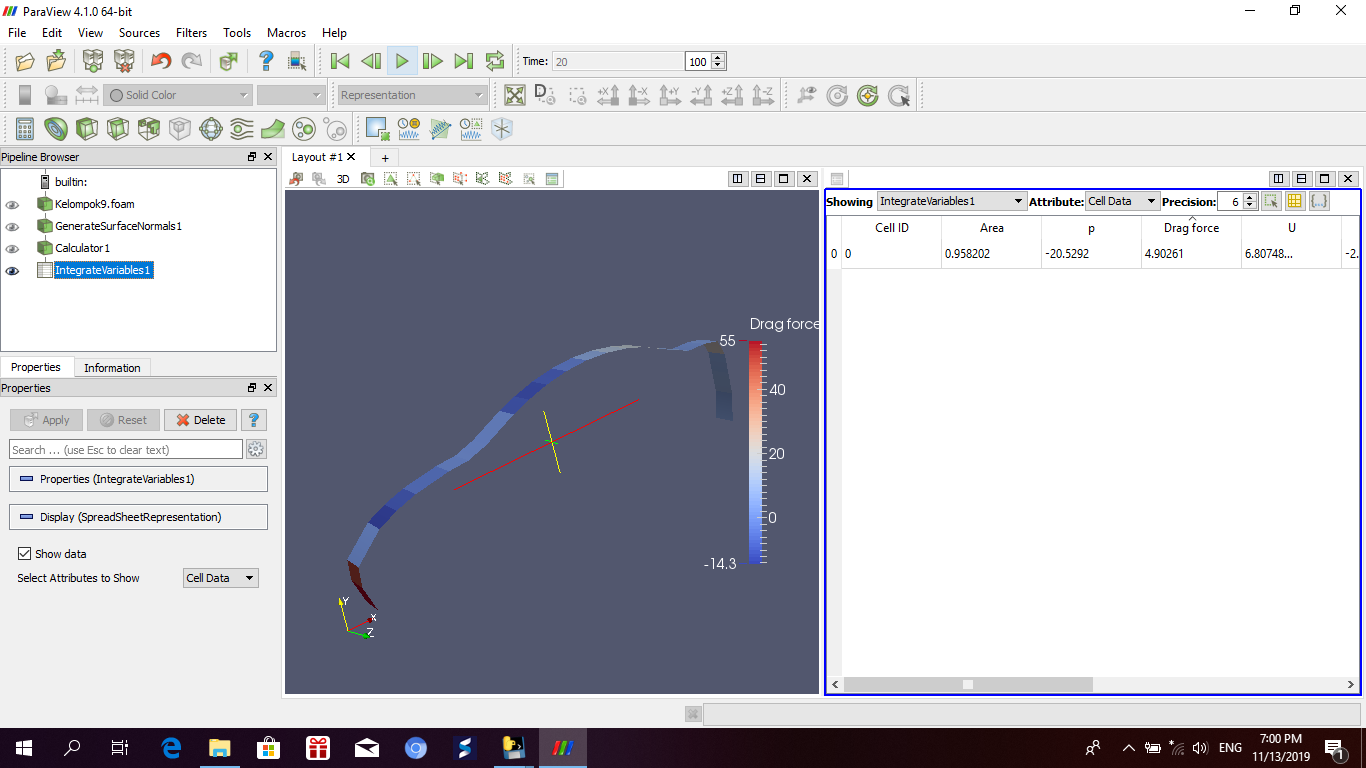
Dragforce in paraview

kami mengawali pengambilan data kecepatan dari kecepatan 20m/s hingga 80m/s. dalam pengambilan data kecepatan kami melakukan dengan kenaikan 5 m/s maka akan didapat sebagai berikut:

Tugastugas.png

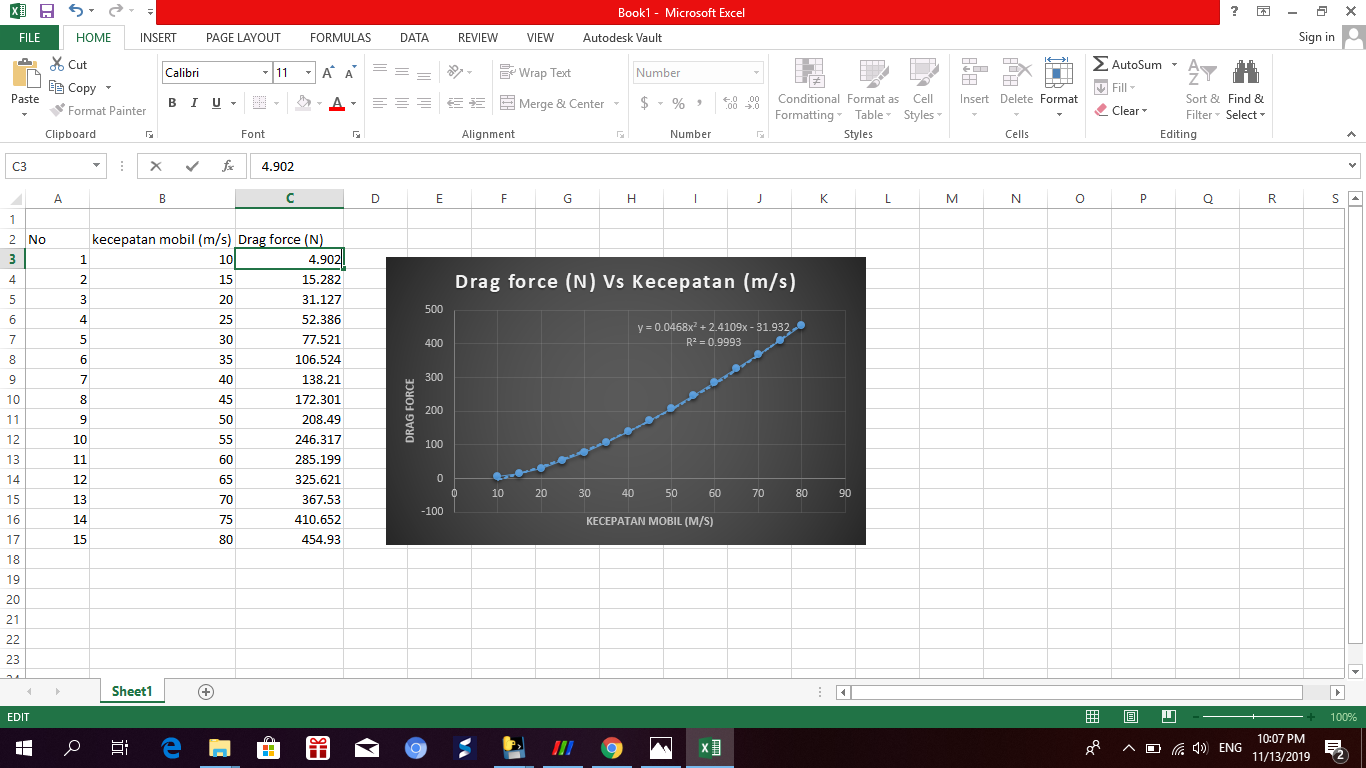
Hasil data dan plotting curve

Dalam hasil data dan plotting ini kami menggunakan hubungan drag force dengan kecepatan. setiap kecepatan mobil akan di plotting dan dilakukan curve fitting

Curvefittingkel9rev.png

hasil curve fitting yang kami lakukan di excel menunjukkan bahwa kurva antara kecepatan terhadap gaya drag menunjukkan hubungan berupa persamaan polinominal dalam hal ini merupakan polinimial pangkat 2. menurut kami hasil curve fitting ini cukup akurat, karena nilai R kuadrat mendekati 1.

karena kkecepatan dan drag force sesuai dengan persamaan berikut maka

Ininiini.png


Sehingga

Inini2.png

karena kecepatan pada tugas pertama nilai kecepatan = 40 m/s maka nilai drag forcenya adalah

Edietdoeloeniech.png


Tugas 3

Airfoil

Airfoil merupakan suatu struktur aerodinamika yang banyak digunakan baik pada sayap pesawat maupun mesin - mesin fluida seperti pompa, kompresor, dan turbin. Airfoil pada sayap pesawat digunakan untuk mengangkat badan pesawat. Perbedaan tekanan antara bagian atas dan bawah airfoil menyebabkan pesawat mendapat gaya angkat


Airfoil yang diteliti

1. Tipe airfoil yang digunakan adalah airfoil NACA 0012. 2. Fluida kerja yang digunakan adalah udara yang mengalir secara steady flow, incompressible, viscous, dan uniform pada aliran freestream inlet. 3. Simulasi dilakukan pada kondisi adiabatik. 4. Penelitian tidak mengikutsertakan analisa bahan yang diguanakan. 5. Airfoil merupakan benda tegar yang tidak berdeformasi.

Karakteristik airfoil

Karakteristik aerodinamika yang meliputi: a. Total lift coefficient (Cl) b. Total drag coefficient (Cd)


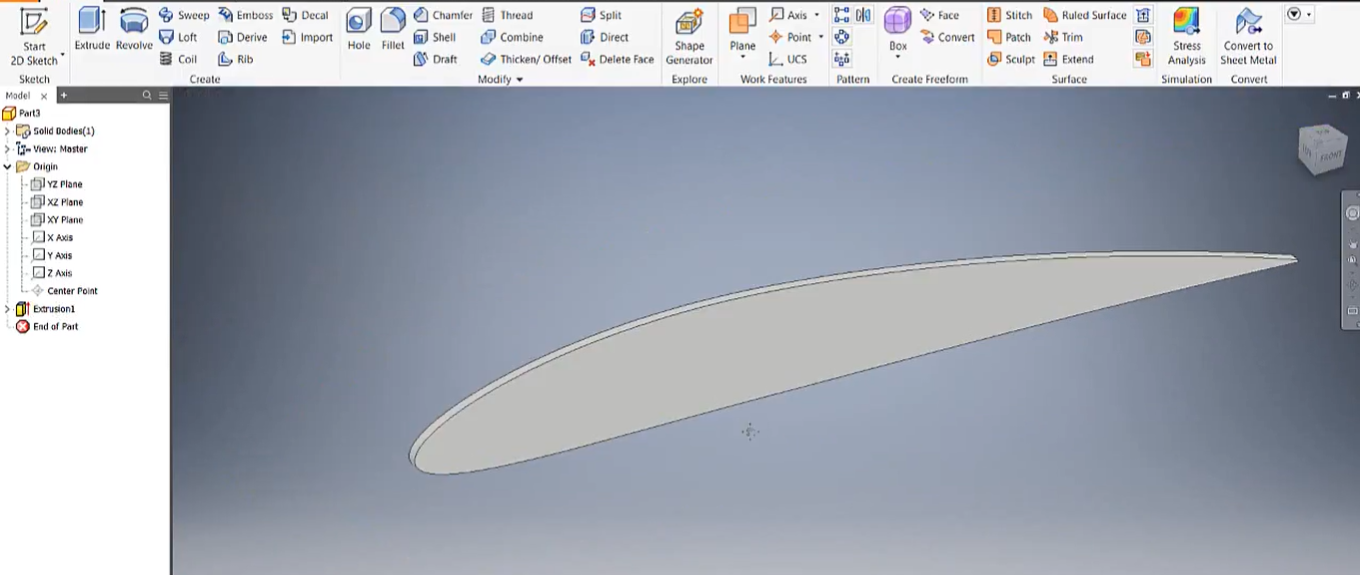
Pembuatan airfoil di Inventor

Tugaskuy.png

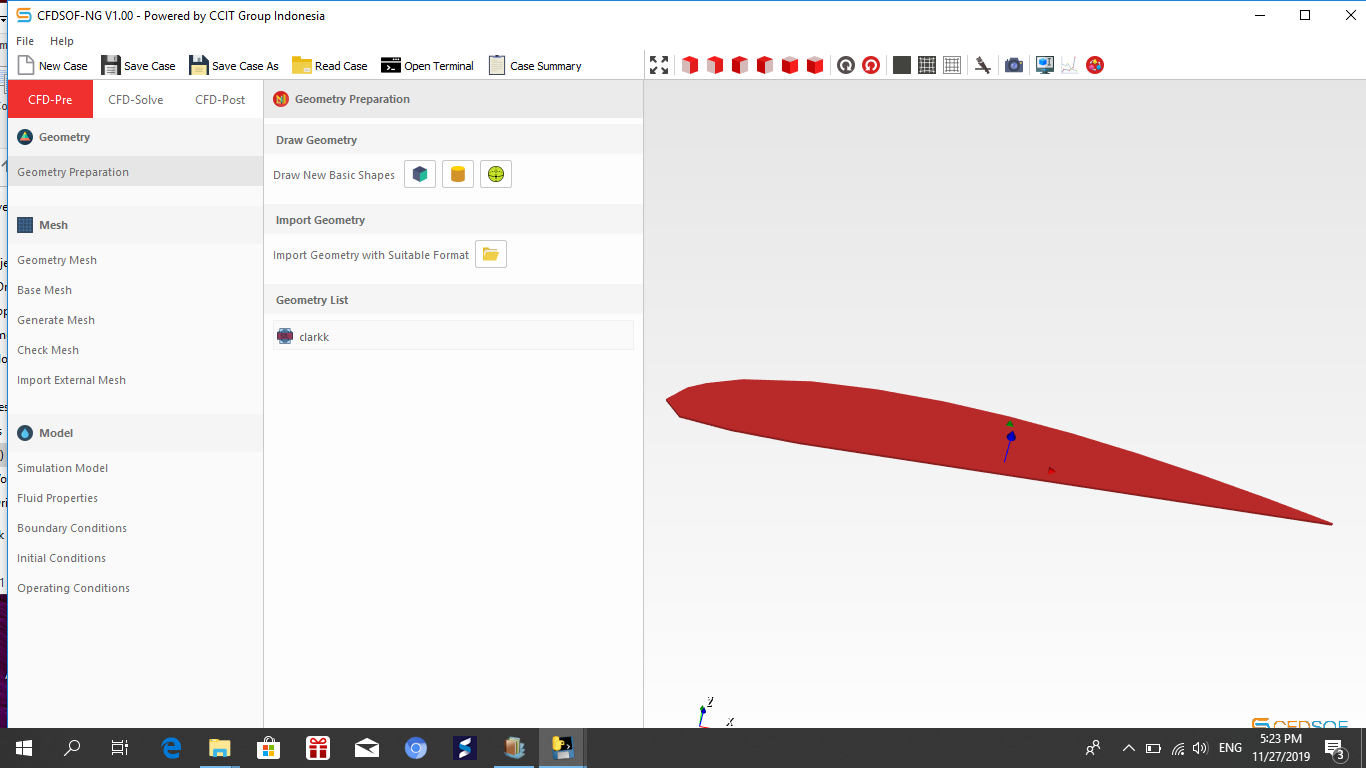
Pemindahan airfoil dari inventor ke CFD Sof

Tugaskuy1.png

Proses Meshing pada CFD Sof

Tugaskuy2.png

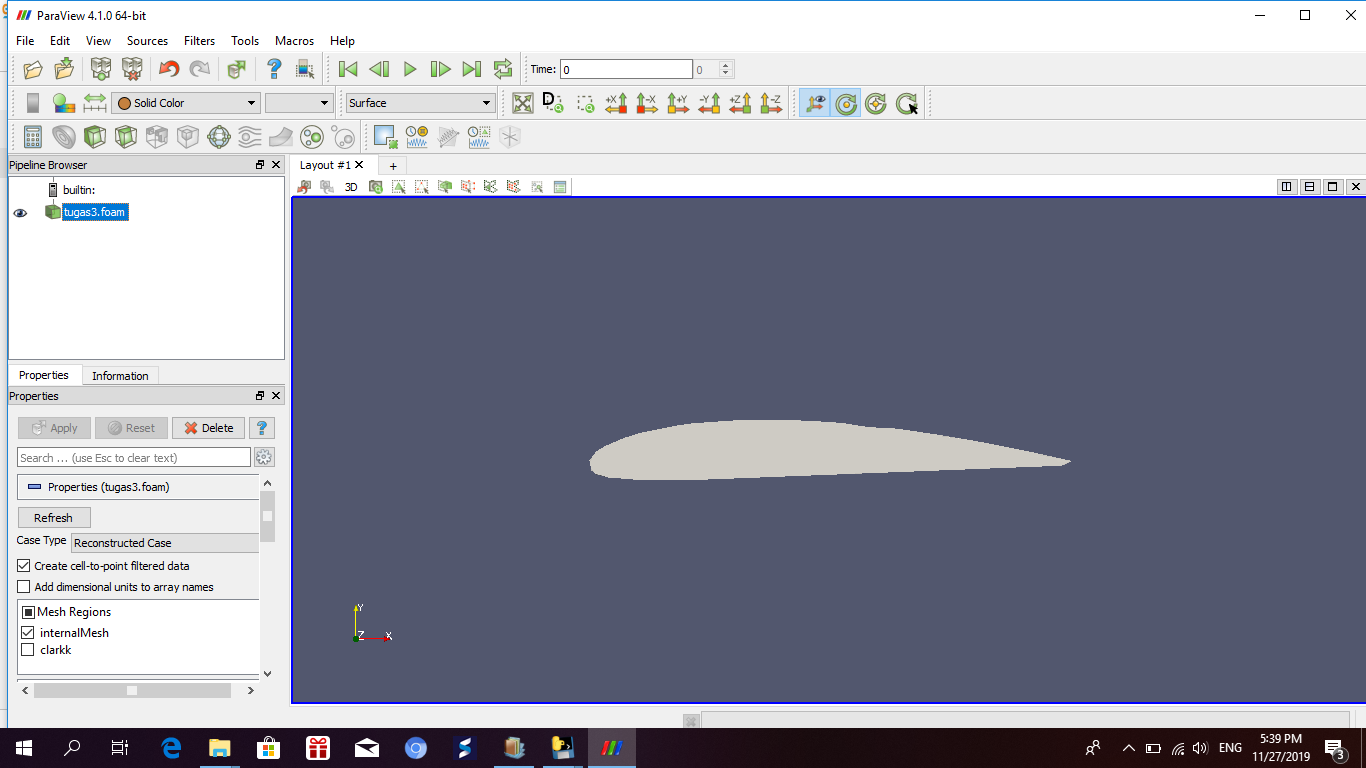
Penghitungan force drag and force lift di paraview

Tugaskuy3.png

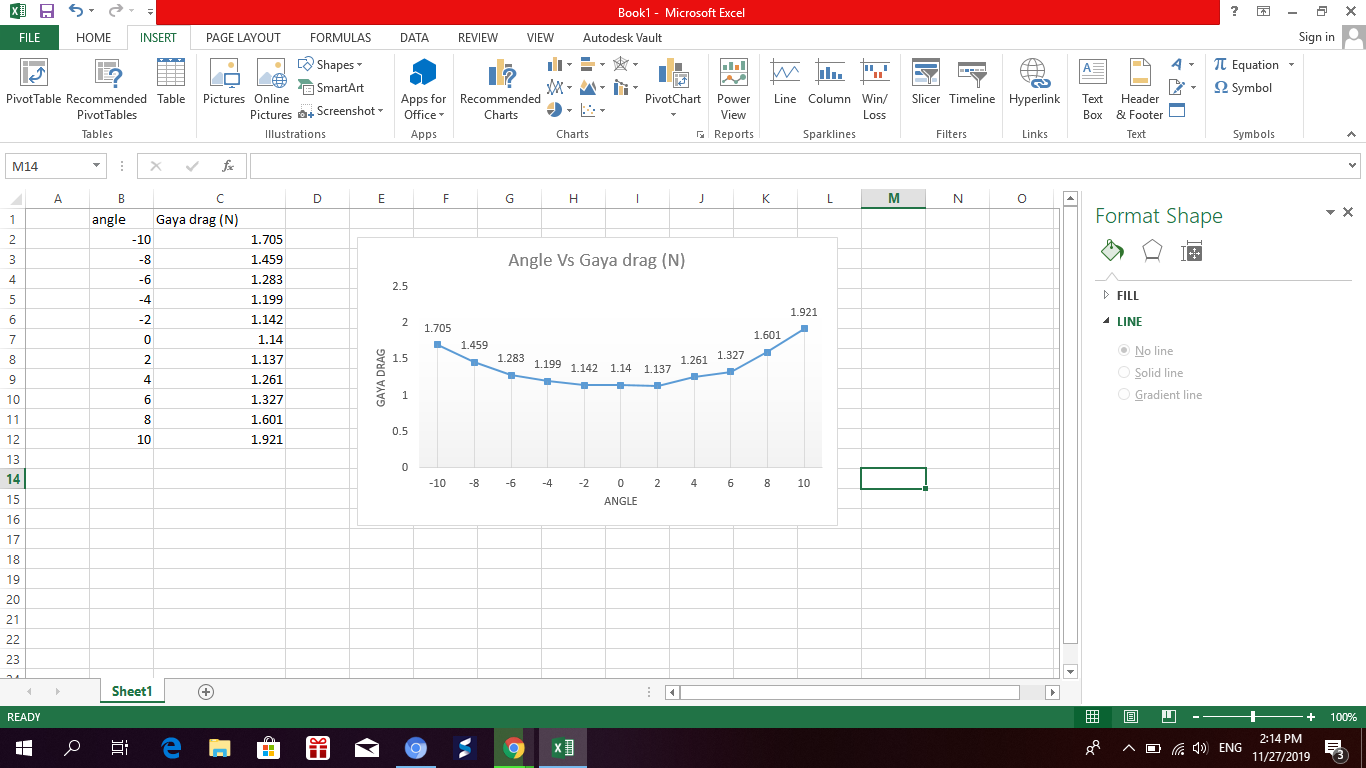
Hasil grafik angle vs gaya drag

Tugaskuy4.png

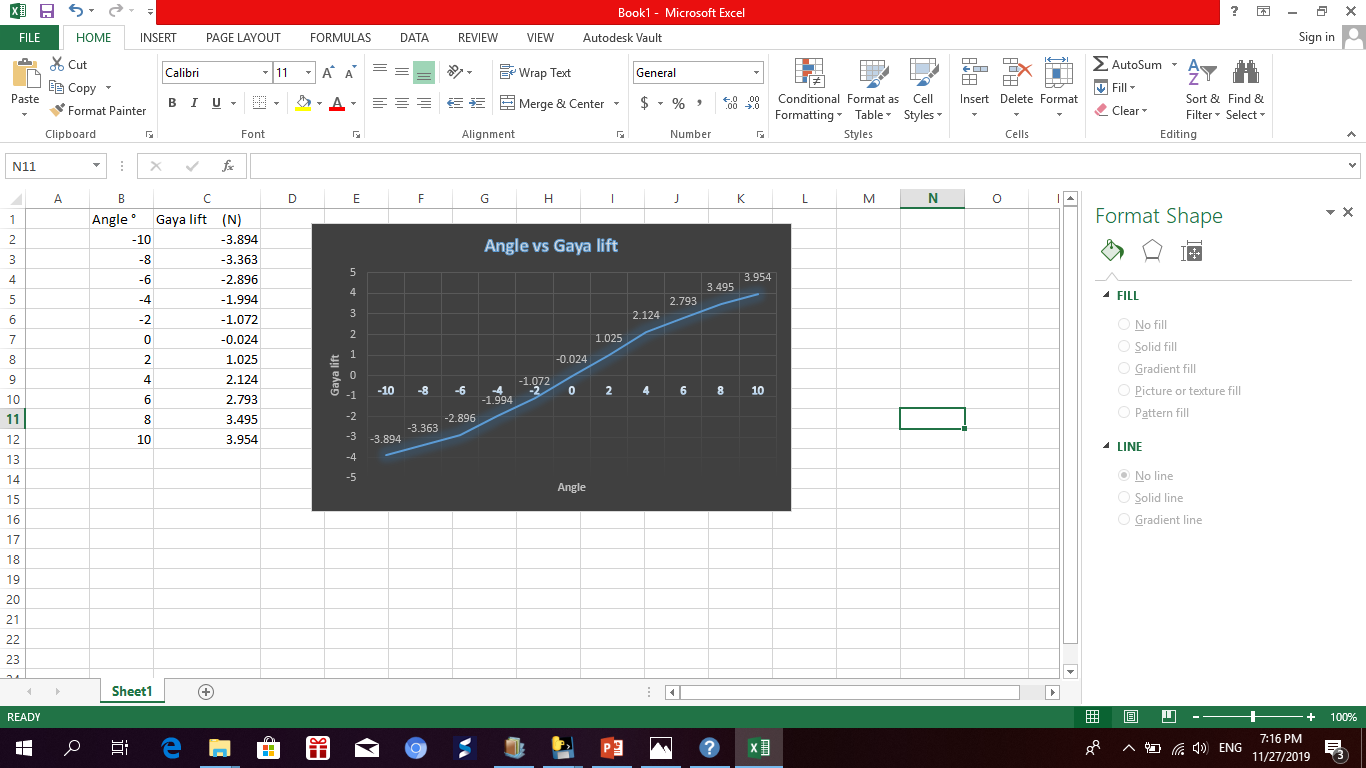
Hasil grafik angle vs gaya lift

Tugaskuy5.png

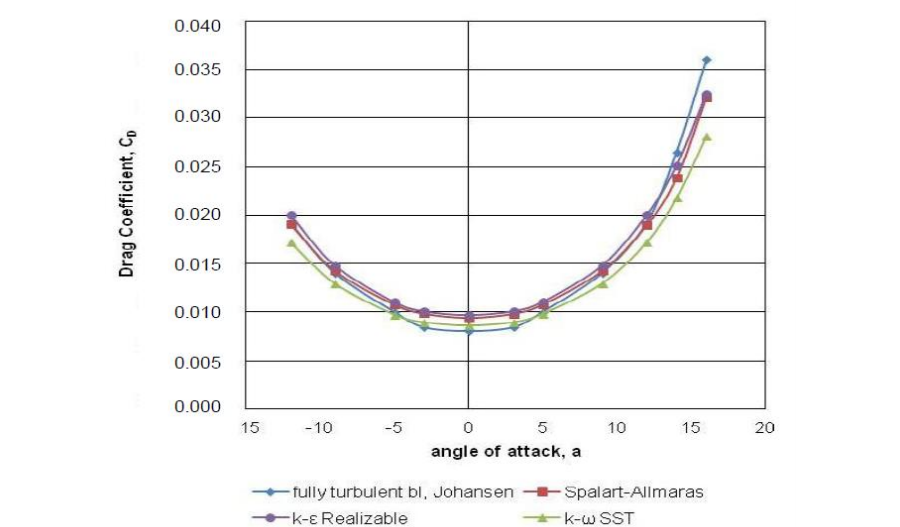
grafik angle vs Cd

Tugaskuy6.png

grafik angle vs Cl

Tugaskuy7.png


Optimasi

  1. !/usr/bin/env python
  2. coding: utf-8
  1. In[11]:


import numpy as np from scipy.optimize import minimize


def calc_drag(x):#drag 

   x1 = x[0]
   drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716
   return drag

def calc_lift(x): #lift 

   x1 = x[0]
   lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313
   return lift

def objective(x): #volume yang diminimalkan 

   return calc_drag(x)

def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag 

   return 90 - calc_drag(x)

def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift 

   return 90 - calc_lift(x)

con1=({'type':'ineq','fun':constraint1}) con2=({'type':'ineq','fun':constraint2}) cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess])

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x forceopt = -sol.fun

dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal

print ('sudut optimal = '+str(-xopt[0])) print ('total force optimal = '+str(forceopt)) print ('drag force optimal = '+str(-dragopt)) print ('lift force optimal = '+str(liftopt))


  1. In[10]:


import nump as np from scipy.optimize import minimize


def calc_drag(x):#drag 

   x1 = x[0]
   drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716
   return drag

def calc_lift(x): #lift 

   x1 = x[0]
   lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313
   return lift

def objective(x): #volume yang diminimalkan 

   return calc_lift(x)

def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag 

   return 90 - calc_drag(x)

def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift 

   return 90 - calc_lift(x)

con1=({'type':'ineq','fun':constraint1}) con2=({'type':'ineq','fun':constraint2}) cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess])

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x forceopt = -sol.fun

dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal

print ('sudut optimal = '+str(xopt[0])) print ('total force optimal = '+str(-forceopt)) print ('drag force optimal = '+str(dragopt)) print ('lift force optimal = '+str(liftopt))


  1. In[ ]:


Hasil optimasi

Hasil optimasi minimum Fd/Fl = -0,29198

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Report_Tugas_Kelompok_9_:_Metode_Numerik_2019&oldid=16791"