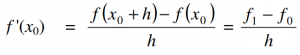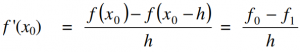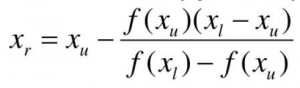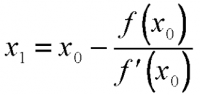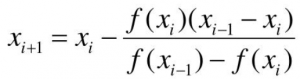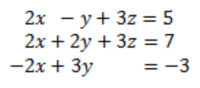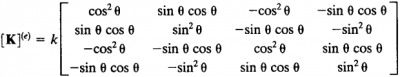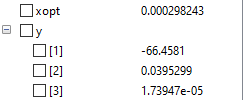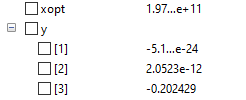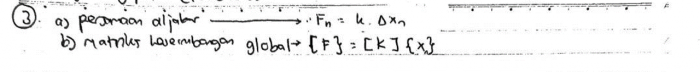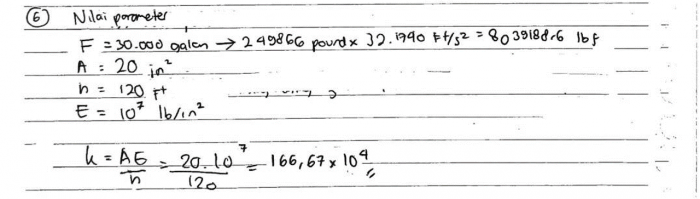Metnum03-Raditya Aryaputra Adityawarman
Contents
- 1 Biodata Diri
- 2 Pertemuan 1: Senin, 9 November 2020
- 3 Pertemuan 2: Senin, 16 November 2020
- 4 Pertemuan 3: Senin, 23 November 2020
- 5 Pertemuan 4: Senin, 30 November 2020
- 6 Pertemuan 5: Senin, 7 Desember 2020
- 7 Pertemuan 6: Senin, 14 Desember 2020
- 8 Pertemuan 7: Senin, 21 Desember 2020
- 9 Tugas Besar Metode Numerik
- 10 UJIAN AKHIR SEMESTER
Biodata Diri
Nama: Raditya Aryaputra Adityawarman
NPM:1806181691
Program Studi: S1 Teknik Mesin Paralel
Kelas: Metode Numerik-03
Pertemuan 1: Senin, 9 November 2020
Pada pertemuan pertama setelah UTS, Pak Dai memberikan arahan kepada kami untuk memanfaatkan air.eng.ui.ac.id sebagai bahan untuk belajar. Selain itu, Pak Dai menjelaskan 4 indikator penilaian untuk pembelajaran metode numerik. Indikator pertama adalah memahami konsep dan prinsip. Konsep yaitu gagasa pemikiran mengenai apa saja yang sudah dipelajari, sedangkan prinsip yaitu pemahaman kita dalam memasukkan rumus-rumus. Indikator kedua adalah menerapkan konsep tersebut dalam memecahkan sebuah masalah. Indikator ketiga memahami aplikasi metode numerik ke dalam masalah keteknikan. Indikator yang terakhir adalah nilai tambah dalam mengenal diri kita sendiri sebagai tolak ukur apakah dari pembelajaran metode numerik diri kita bisa berkembang
Materi Sebelum UTS
Pada pertemuan sebelum UTS, kami telah belajar 3 materi utama, yaitu turunan numerik, mencari akar-akar, dan membaca pola.
1. Turunan Numerik
- turunan numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menentukan turunan:
- Turunan maju
- Turunan mundur
- Turunan pusat
2. Mencari Akar
- Pada materi ini, kami belajar cara mencari akar dengan metode numerik. Ada 2 cara dalam mengerjakannya, yaitu bracketing method dan open method.
- Bracketing method
- Bracketing method adalah metode mencari akar dengan cara menebak dua nilai, kemudian mengurung kedua nilai tersebut sehingga kita dapat menemukan akar-akar dari persamaan. Pada metode ini, ada beberapa cara penyelesaian, yaitu metode graphical, metode bisection, dan false-position.
- Metode Graphical
- Metode ini digunakan dengan cara membuat grafik fungsi dan melihat perpotongan sumbu horizontal atau sumbu x.
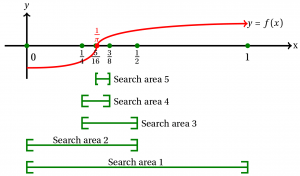
- Metode Bisection
- Metode ini dilakukan dengan cara membagi dua kurva yang diwakili oleh suatu titik yang nilainya dikalikan oleh nilai tertinggi dan yang terendah. Metode ini terus dilakukan hingga menemukan akar.
- False Position
- Metode ini mirip dengan bisection, namun bedanya untuk penentuan titik tengah menggunakan segitiga dari titik perpotongan kurva dengan garis yang ditentukan.
- Open Method
- Metode ini hanya menggunakan 1 titik sebagai acuan pertama untuk menemukan akar yang dicari. Open method terbagi menjadi 3 cara, yaitu newton rhapson, secant, dan simple fix point.
- Newton Rhapson
- Metode ini dilakukan dengan cara menentukan suatu titik dan menarik garis singgung terhadap kurva. Cara menentukan garis singgung tersebut dengan turunan.
- Secant
- Metode ini mirip dengan Newton Rhapson, tapi estimasi dengan 2 titik jika pada newton rhapson f'(x) tidak dapat dicari.
- Simple Fix Point
- Metode ini menghitung seluruh kemungkinan x yang dihasilkan dan dicari x konvergen sehingga x=g(x).
3. Membaca Pola
- Ada dua cara dalam membaca pola suatu data, yaitu dengan regresi dan interpolasi
- Regresi
- Interpolasi
Tugas 1 Software OpenModelica
Saya mempelajari OpenModelica dengan referensi sebagai berikut:
https://www.youtube.com/watch?v=Dw66ODbMS2A&feature=youtu.be
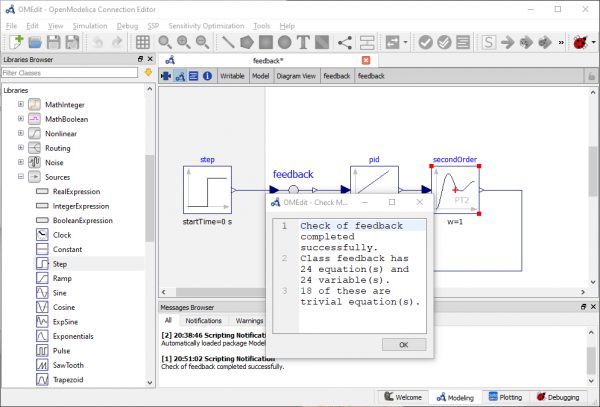
Video tersebut menjelaskan tutorial simulasi feedback control system. Berikut tahapan-tahapan simulasi:
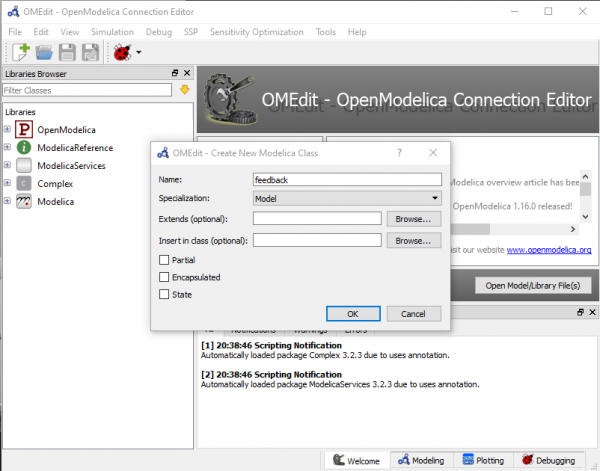
- Pertama, buka OpenModelica dengan nama feedback
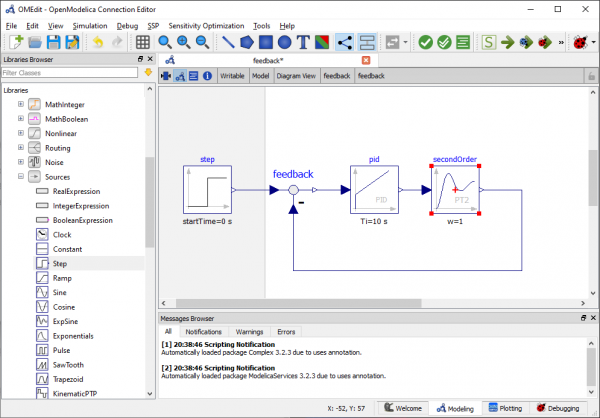
- Semua diagram blok yang akan disimulasikan terdapat pada tab blocks modelica. Pada simulasi ini, saya menggunakan sistem linear dan simple second order system untuk kontrol.
- Kemudian saya memakai PID controller pada menu continuous
- Pilih blok PID dan second order
- Pada menu math, pilih blok feedback
- Pada menu sources, pilih step sebagai input
- Setelah itu, blok-blok tersebut dihubungkan dengan cara menarik garis antar blok sehingga sistem menjadi closed loop
- Kemudian mengatur parameter yang diinginkan. Sistem tersebut underdamped, sehingga nilai damping yang dimasukkan <0.7
- Cek model apakah sudah siap untuk diset up atau belum
- Setelah siap untuk disimulasikan, kita menyimpan terlebih dahulu pada tempat default
- Jalankan simulasi dan tunggu hingga selesai
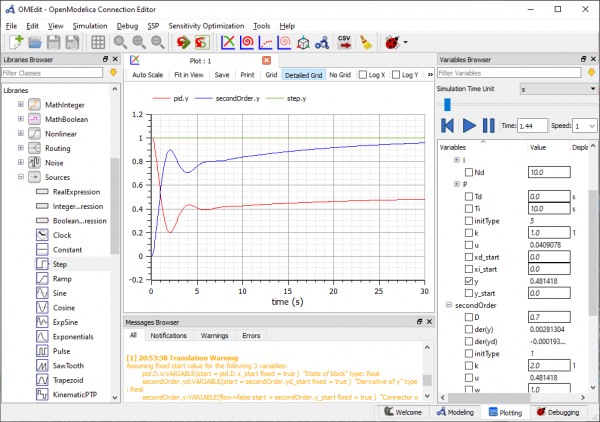
- Setelah simulasi selesai dilakukan, untuk melihat kurva centang y pada PID, step, dan second order
- Hasil simulasi didapatkan. Kita bisa mengubah parameter sehingga hasil simulasi lebih jelas
Lampiran
Pertemuan 2: Senin, 16 November 2020
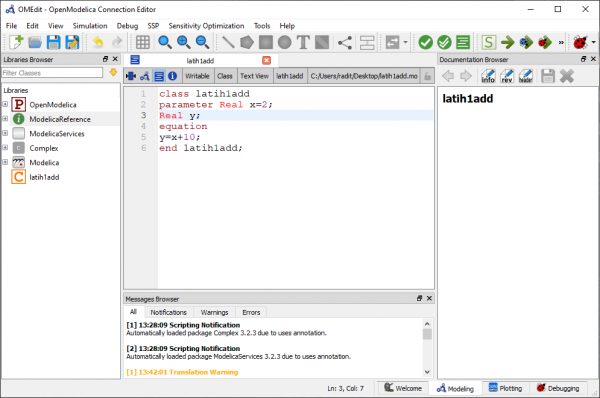
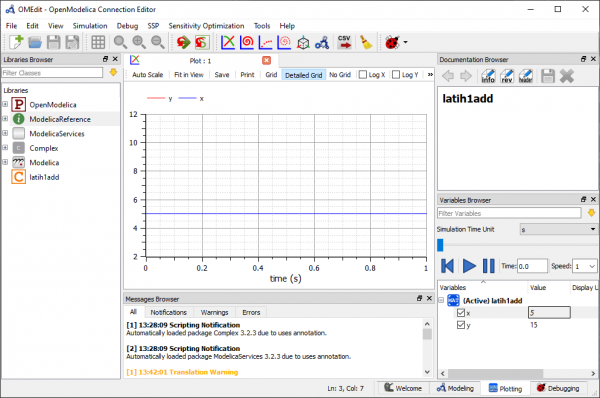
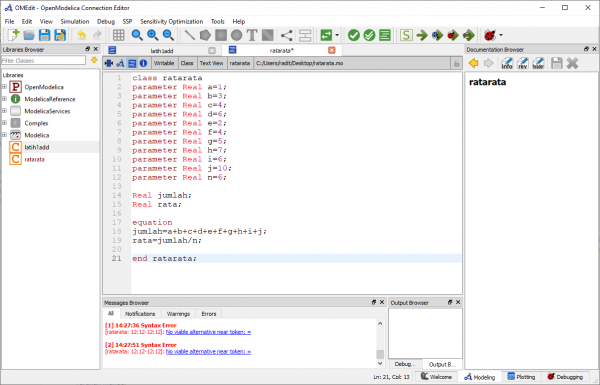
Pada pertemuan ini, Pak Dai meminta setiap mahasiswa menunjukkan tugas minggu lalu, yaitu belajar OpenModelica. Lalu kami simulasi membuat program sederhana didalam modelica untuk menjumlahkan angka 10 kepada sebuah variabel. Berikut parameter dan hasilnya:
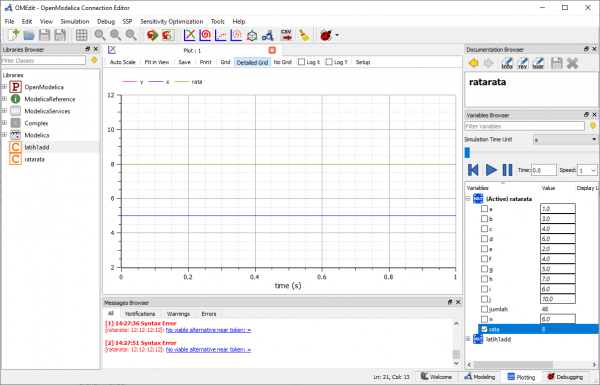
Lalu kami diminta untuk membuat program untuk mencari nilai rata-rata. Berikut parameter dan hasilnya:
Tugas 2 Menyelesaikan Aljabar Simultan
Pada tugas ini saya menggunakan persamaan berikut untuk mengerjakan tugas 2.
Dalam hal ini, bisa dilakukan beberapa metode dalam mengerjakannya, seperti menggunakan eliminasi gauss, gauss jordan, crammer, dan gauss seidel.
- Eliminasi gauss adalah suatu tahapan untuk memecahkan persamaan dengan cara mereduksi / menyederhanakan matriks persamaan tersebut. Prosedur dalam metode Gauuss akan menghasilkan bentuk matrik pada eselon tereduksi.
- Gauss jordan merupakan pengembangan metode eliminasi Gauss, hanya saja augmented matrik, pada sebelah kiri diubah menjadi matrik diagonal.
- Metode Cramer menggunakan determinan suatu matriks dan matriks lain yang diperoleh dengan mengganti salah satu kolom dengan vektor yang terdiri dari angka di sebelah kanan persamaannya.
- Gauss seidel digunakan untuk menyelesaikan sistem persamaan linear (SPL) berukuran besar dan proporsi koefisien nolnya besar, seperti sistem-sistem yang banyak ditemukan dalam sistem persamaan diferensial.
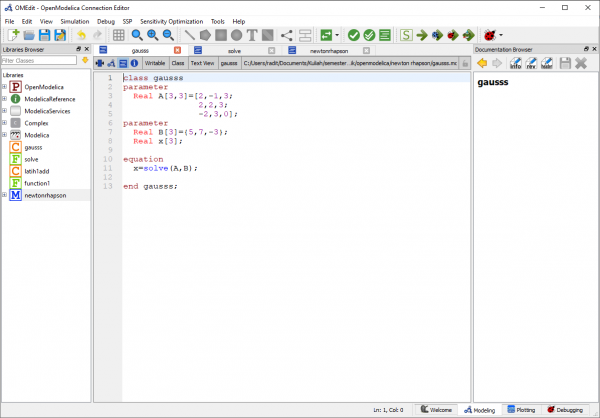
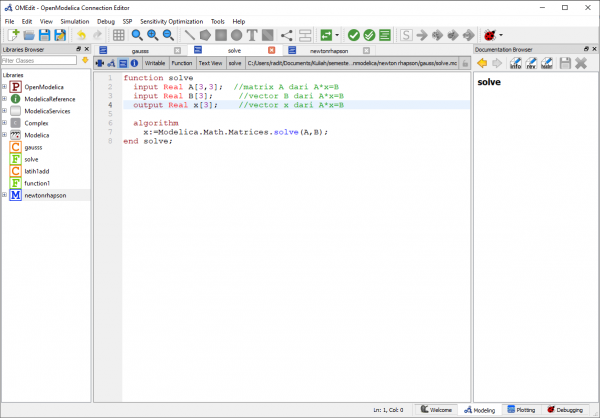
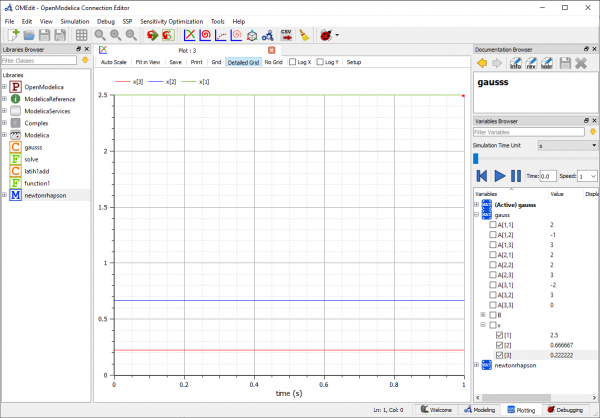
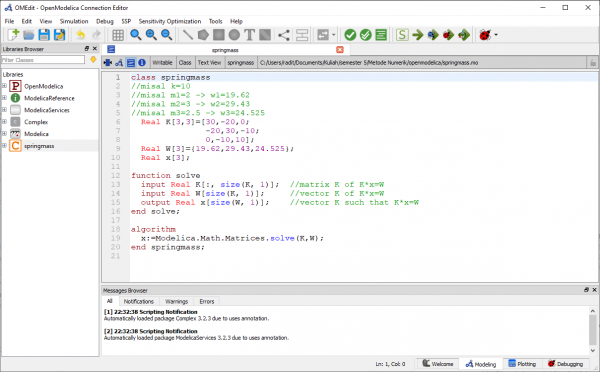
Pada tugas ini, saya memakai metode eliminasi gauss dalam menyelesaikannya. Berikut percobaan yang saya lakukan:
Dari simulasi ini didapatkan hasil x=2.5, y=0.66667, dan z=0.22222
Referensi dari percobaan di atas didapat dari https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html.
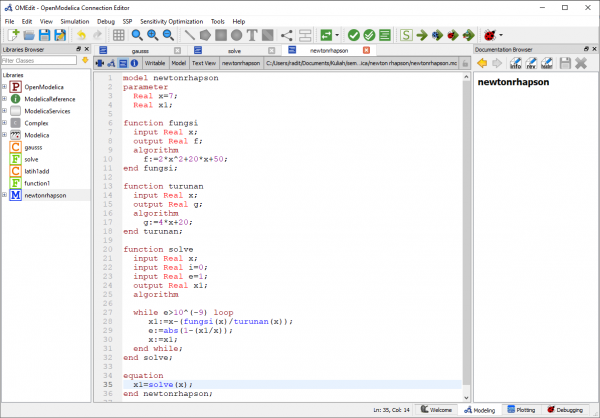
Selain itu, saya mencoba membuat persamaan Newton Rhapson. Metode ini dilakukan dengan cara menentukan suatu titik dan menarik garis singgung terhadap kurva. Cara menentukan garis singgung tersebut dengan turunan. Kelebihan dari metode ini adalah hasilnya didapatkan dengan cepat, hanya memerlukan satu titik saja, dan caranya sederhana. Namun, kekurangan dari metode ini adalah tidak semua persamaan konvergen sehingga beberapa persamaan tidak mempunyai solusi dengan metode ini. Selain itu ketika memilih titik yang turunannya=0, cara ini tidak bisa digunakan.
Pertama-tama saya membuat fungsi pada function. Persamaan yang saya gunakan yaitu y=2x^2+20x+50. Selanjutnya, saya membuat fungsi turunan dengan persamaan y'=4x+20.
Kemudian saya membuat rumus newton rhapson pada function solve. Rumusnya yaitu Xn=(xn-1)-(f(xn-1)/f'(xn-1)). Input yang dimasukkan x0, i=0, dan x1. X sebagai variabel yang dimasukkan. Sementara i merupakan iterasi. Saya menggunakan loop while, sehingga program terus melakukan looping selama error lebih besar dari 10^-9.
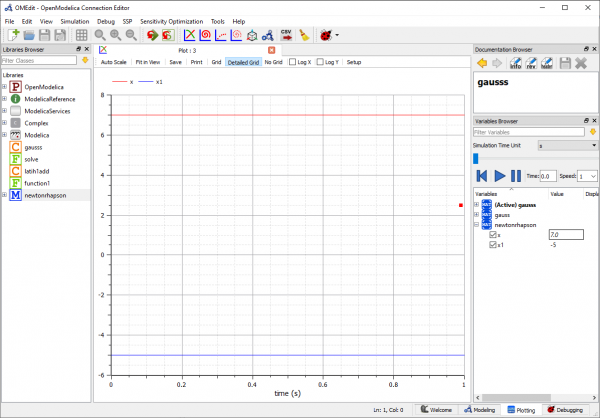
Lalu saya membuat equation. Equation ini untuk menghitung fungsi-fungsi yang sudah dibuat. Parameternya yaitu x0=7 dan x1. x0=7 merupakan titik yang ditentukan.
Setelah dilakukan simulasi, maka didapatkan hasil dari persamaan y=2x^2+20x+50 yaitu titik yang memotong garis horizontal x=-5.
Pertemuan 3: Senin, 23 November 2020
Pada pertemuan ini, kami diminta untuk menjelaskan tugas minggu lalu, yaitu penyelesaian aljabar simultan. Selain itu, Pak Dai menjelaskan aplikasi metode numerik dalam permasalahan teknik. Urutan penyelesaiannya yaitu:
- masalah teknik, yaitu tahapan membuat gambaran mengenai masalah yang ada, seperti parameter dan metode yang digunakan.
- analisis masalah, yaitu respon dari kasus yang ada. Pada tahap ini menganalisis permasalahan dari parameter-parameter yang sudah diketahui
- model matematis, membuat model matematika dari variabel yang ada dengan hukum fisika.
- model numerik, yaitu menggunakan bahasa pemrograman untuk menyelesaikan permasalahan yang ada, contohnya menggunakan open modelica untuk menyelesaikan aljabar simultan.
- komputer, yaitu menggunakan software untuk menyelesaikan perhitungan, seperti open modelica, cfdsof, mathlab, dll.
- solusi, hasil dari simulasi didapatkan.
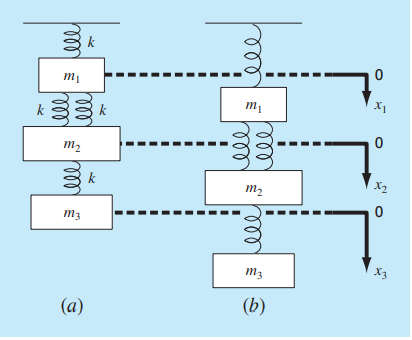
Selanjutnya Pak Dai memberi tugas untuk menyelesaikan permasalahan pegas massa yang terdapat pada bab 12 dari buku Numerical Method. Berikut soalnya:
Untuk menyelesaikan soal ini, pertama-tama membuat free body diagram dari masing-masing sistem. Kemudian menuliskan persamaannya. Setelah itu, persamaan tersebut dapat diselesaikan dengan metode numerik, yaitu membuat matriks dan diselesaikan dengan eliminasi gauss. Berikut kode yang digunakan:
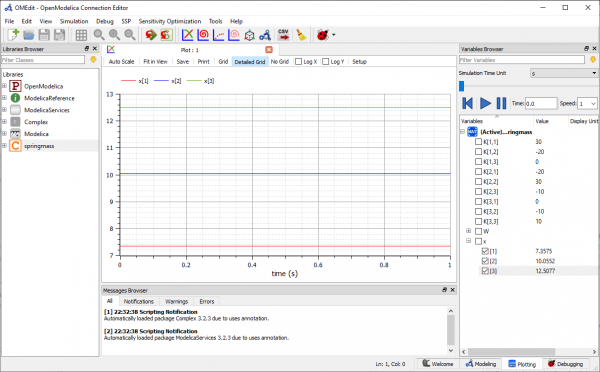
Berikut hasilnya, di mana x1 = 7,36, x2 = 10,06, x3 = 12,51
Tugas 3 Menghitung Displacement dan Gaya Reaksi pada Trusses
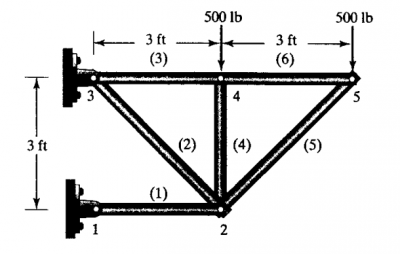
Tugas yang diberikan pada pertemuan ketiga yaitu menghitung displacement dan gaya reaksi pada balcony truss dengan metode Finite Element Analysis (FEA) menggunakan aplikasi open modelica.
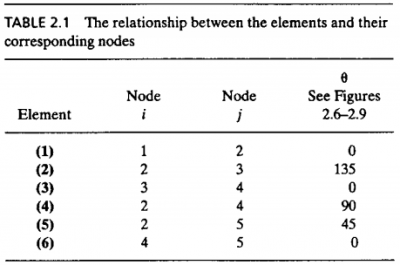
Penyelesaiannya sebagai berikut: 1.Pertama-tama, menentukan elemen-elemen setiap batang, menentukan sudut, dan node-nodenya.
2.Lalu menentukan kekakuan setiap batang. Rumus dari konstanta kekakuan yaitu k=AE/L dengan A luas penampang, E modulus elastisitas, dan L panjang batang. Karena batang 1,3,4,6 mempunyai panjang yang sama sebesar 36 in maka k juga sama. Begitu pula dengan k pada batang 2 dan 5 dengan panjang 50.9 in.
3. Kemudian membuat persamaan matriks pada elemen. Rumusnya sebagai berikut:
Persamaan tersebut kemudian dihitung pada tiap elemen menjadi matriks lokal. Dalam perhitungan, perhatikan juga nodenya karena akan dimasukkan ke dalam matriks global.
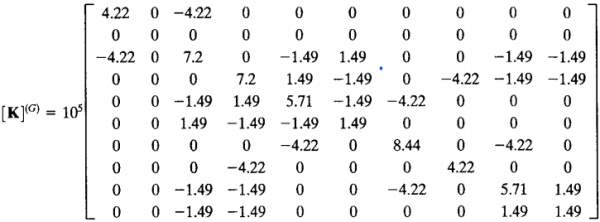
4. Gabungkan semua matriks lokal tiap elemen ke matriks global. Rumusnya: [K]G=[K1]+[K2]+[K3]+[k4]+[k5]+[k6]
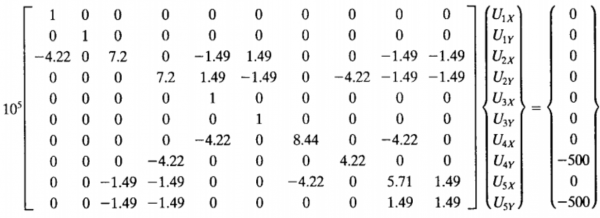
5. Lalu masukkan boundary conditionnya. Pada node 1 dan 3 fix, sehingga U1x,U1y,U3x,U3y=0. Pada node 4 dan 5 diberikan gaya eksternal dengan F4y = -500 lb dan F5y = -500 lb. Boundary condition tersebut kemudian dimasukkan dalam persamaan {F}=[K]g*[U].
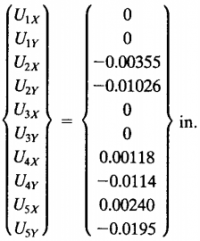
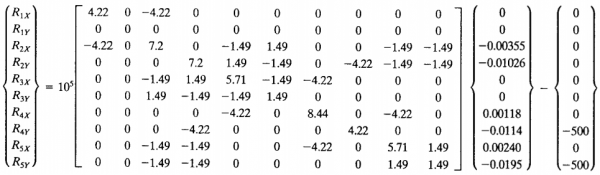
6. Dari matriks tersebut bisa diselesaikan dengan eliminasi gauss, menghasilkan displacement U2x=-0.00355 in, U2Y=-0.01026 in, U4x=0.00118 in, U4y= -0.0114 in, U5x = 0.00240 in, dan U5y = -0.0195 in. Berikut matriks globalnya:
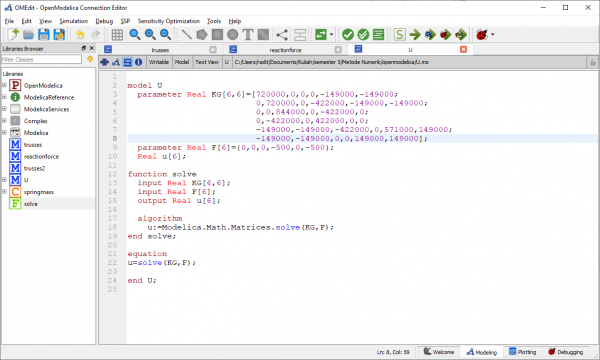
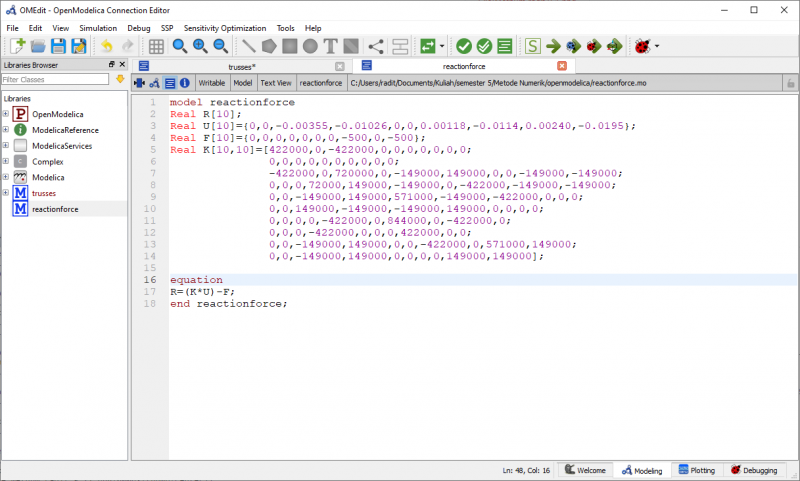
Berikut kode yang sudah saya buat dalam aplikasi openmodelica:
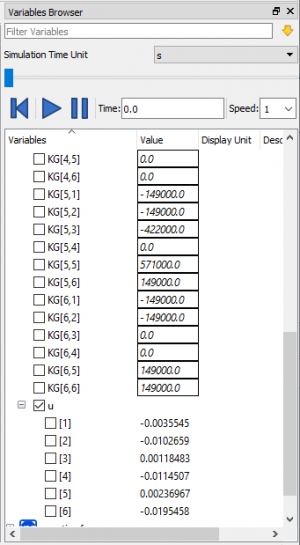
Berikut hasilnya:
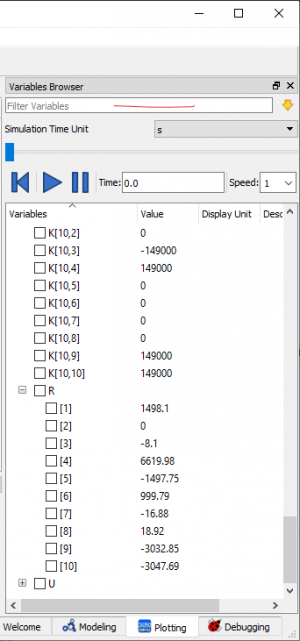
7. Kemudian menentukan gaya reaksi dengan rumus {R}=[K]g{U}-{F}. Berikut hasilnya:
Berikut kode yang sudah saya buat dalam aplikasi openmodelica:
Berikut hasilnya:
Berikut file openmodelica yang saya buat: https://drive.google.com/drive/folders/1VxlNZBhgml-QFlUVyLImvTKod26Yo2i7?usp=sharing
Pertemuan 4: Senin, 30 November 2020
Quiz
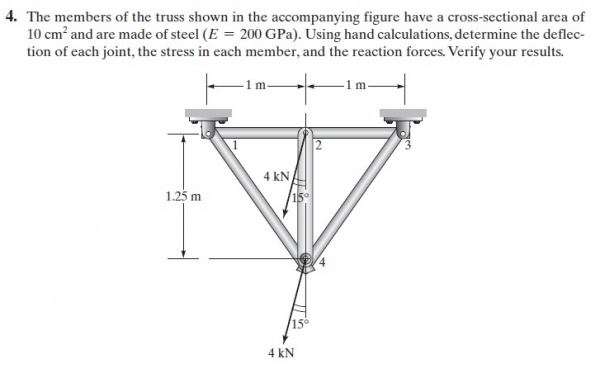
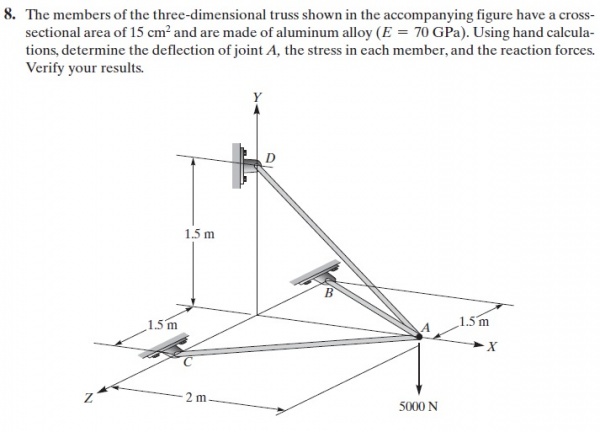
Pada pertemuan ini diberikan quiz menghitung defleksi dan gaya reaksi dengan menggunakan Openmodelica. Berikut soal yang diberikan:
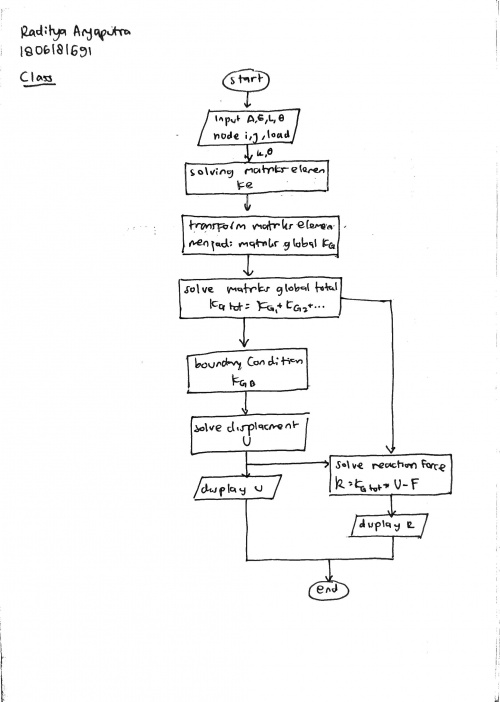
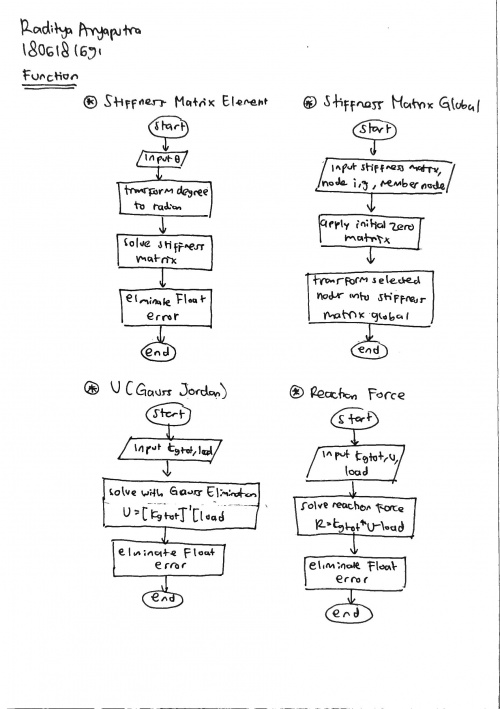
Berikut flow chart urutan pengerjaan soal di atas:
Kemudian berikut cara manual mengerjakan soal nomor 4 dan 8:
Berikut kode yang saya gunakan dalam mengerjakan soal nomor 4:
Fungsi Utama
Sebelum disederhanakan
class truss
//Data inisiasi [elemen #, node i, node j, theta(degrees), area(m^2), modulus(Pa), panjang(m)]
parameter Real [:,7] inisiasi = [1, 1, 2, 0, 10e-4, 200e9, 1.00;
2, 2, 3, 0, 10e-4, 200e9, 1.00;
3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
4, 2, 4, 270.00, 10e-4, 200e9, 1.25;
5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
//Data node [node i, node j]
parameter Integer [:,2] node = [1, 2;
2, 3;
1, 4;
2, 4;
3, 4];
//External load pada tiap node [node #, FX, FY]
parameter Real [:,3] node_load = [1, 0, 0;
2, -1035.28, -3863.70;
3, 0, 0;
4, -1035.28, -3863.70];
parameter Integer y = size(node,1); //jumlah node
parameter Integer x = 2*(size(node_load,1)); //total node tiap batang
parameter Integer [:] Boundary = {1,3}; //node pada boundary
parameter Real [x] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70}; //load tiap node
Integer z = sum(Boundary); //jumlah boundary
Real [y] k;
Real [y,4,4] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,5] * inisiasi[i,6] / inisiasi[i,7]) for i in 1:size(inisiasi,1)}; //stiffness constant
Ke = StiffnessMatrixElement(inisiasi); //matriks lokal
Kg = StiffnessMatrixGlobal(node, x, y, Ke); //matriks global
KgTot = SumStiffnessMatrixGlobal(x,y,Kg); //total matriks global
KgB = BoundaryStiffnessMatrixGlobal(x,z,KgTot,Boundary); //boundary
U = GaussJordan(x,KgB,load); //displacement
R = ReactionForce(x,KgTot,U,load); //reaction force
end truss; |
Matriks elemen
function StiffnessMatrixElement
input Real [:,7] inisiasi_mat;
output Real [size(inisiasi_mat,1),4,4] Ke_mat;
protected
Real theta;
Real [3] StiffTrig;
Real [4,4] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
Real float_error = 10e-10;
algorithm
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / inisiasi_mat[i,7]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(3);
StiffTrans := zeros(4,4);
// Converting degrees to radians
theta := Modelica.SIunits.Conversions.from_deg(inisiasi_mat[i,4]);
// {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2,
(Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
// Handle float error elements in StiffTrig
for t in 1:size(StiffTrig,1) loop
if abs(StiffTrig[t]) <= float_error then
StiffTrig[t] := 0;
end if;
end for;
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3];
StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2];
-1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3];
-1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:4 loop
for n in 1:4 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement; |
Matriks Global
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,4,4] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2];
Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1];
Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1];
Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2];
Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4];
Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3];
Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3];
Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4];
Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2];
Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1];
Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1];
Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2];
Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4];
Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3];
Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3];
Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal; |
Total Matriks Global
function StiffnessMatrixGlobal
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] :=sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;Boundary function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:z-1 loop
KgB_met[2*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:z-1 loop
KgB_met[2*Boundary_met[a]-b,z*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal; |
Gauss Jordan
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;Reaction Force function ReactionForce
input Integer x;
input Real [x,x] KgTot_met;
input Real [x] U_met;
input Real [x] load_met;
output Real [x] R_met;
algorithm
R_met := (KgTot_met*U_met)-load_met;
end ReactionForce; |
Pertemuan 5: Senin, 7 Desember 2020
Pada pertemuan ini, kami diminta Pak Dai membahas mengenai proses pengerjaan soal quiz minggu lalu. Lalu Fahmi menjelaskan coding yang dibuat untuk mengerjakan quiz minggu lalu mengenai plane truss dan space truss. Kemudian kami mengerjakan soal truss pada 3 dimensi. Penjelasan yang diberikan Fahmi yaitu penggunaan fungsi for untuk looping, membuat data dalam bentuk array, menggunakan fungsi if, floating number pada komputer dan pengaruh pada hasil simulasi, apa itu protected variable, dan perbedaan antara class dan function.
Selanjutnya kami diberikan tugas untuk minggu depan oleh Pak Dai, yaitu: Tugas untuk Minggu depan
- Mempelajari codingan 3d fahmi
- Mengaplikasikan pada soal example 3.3
- memberikan masukan atas codingan fahmi
Tugas 4:Three dimensional Truss
Masukan pada codingan
Beberapa masukan pada kode yang dibuat fahmi diantaranya:
1. Penyederhanaan parameter sehingga variabel yang dimasukkan lebih sedikit dan tidak berulang-ulang:
Sebelum disederhanakan
parameter Real [:,7] inisiasi = [1, 1, 2, 0, 10e-4, 200e9, 1.00;
2, 2, 3, 0, 10e-4, 200e9, 1.00;
3, 1, 4, 308.66, 10e-4, 200e9, 1.60;
4, 2, 4, 270.00, 10e-4, 200e9, 1.25;
5, 3, 4, 231.34, 10e-4, 200e9, 1.60];
//Data node [node i, node j]
parameter Integer [:,2] node = [1, 2;
2, 3;
1, 4;
2, 4;
3, 4];
//External load pada tiap node [node #, FX, FY]
parameter Real [:,3] node_load = [1, 0, 0;
2, -1035.28, -3863.70;
3, 0, 0;
4, -1035.28, -3863.70];
parameter Integer y = size(node,1); //jumlah node
parameter Integer x = 2*(size(node_load,1)); //total node tiap batang
parameter Integer [:] Boundary = {1,3}; //node pada boundary
parameter Real [x] load = {0,0,-1035.28,-3863.70,0,0,-1035.28,-3863.70}; //load tiap node
Integer z = sum(Boundary); //jumlah boundary |
Setelah disederhanakan
parameter Real [:,5] inisiasi = [1, 0, 8, 1.9e6, 36; //inisiasi
2,135, 8, 1.9e6, 50.9;
3, 0, 8, 1.9e6, 36;
4, 90, 8, 1.9e6, 36;
5, 45, 8, 1.9e6, 50.9;
6, 0, 8, 1.9e6, 36];
parameter Integer [:,2] node = [1, 2; //node = [ i, j]
2, 3;
3, 4;
2, 4;
2, 5;
4, 5];
parameter Integer n = 5; //jumlah node
parameter Integer [:] Boundary = {1,3}; //titik node boundary
parameter Real [:] load = {0,0,0,0,0,0,0,-500,0,-500}; //load = [ F1x, F1y,..., Fnx, Fny] |
2. Memodifikasi fungsi zeros pada kode matrix global karena untuk membuat matriks 0 tidak memerlukan looping
Sebelum disederhanakan
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for; |
Setelah disederhanakan
algorithm
Kg_mat := zeros(size(Ke_mat,1),2*x,2*x); |
3. Penambahan float error pada reaction force sehingga pada pengecekan gaya total (reaction+load) = 0
Sebelum diubah
algorithm
R_met := (KgTot_met*U_met)-load_met; |
Setelah diubah
algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for; |
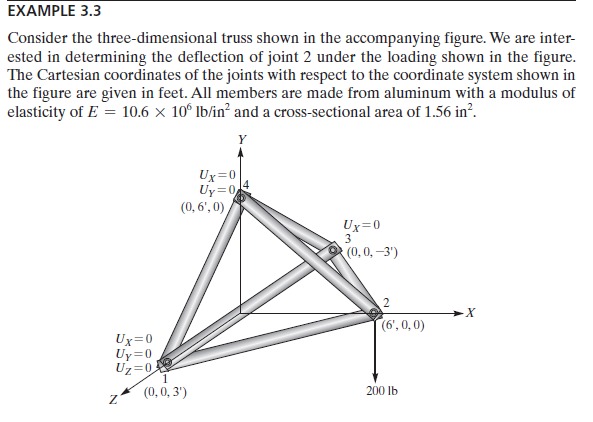
2. Soal example 3.3
Pada soal ini, proses pengerjaan sama dengan soal tugas minggu lalu yang sudah dijelaskan oleh Fahmi. Namun, beberapa parameter diubah karena tidak diketahui sudut dan panjang batangnya, melainkan koordinat node tiap batang. Berikut beberapa parameter yang diubah:
- pada parameter inisiasi, sudut pada batang diubah menjadi selisih dari koordinat node tiap batang
- boundary disesuaikan berdasarkan Ux,Uy,dan Uz pada soal
- dimensi load ditambahkan menjadi Fx,Fy,dan Fz
- penambahan equation panjang dari koordinat node batang
Space truss
class spacetruss
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //inisiasi = [ elemen#, dX, dY, dZ, A, E]
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
parameter Integer [size(inisiasi,1),2] node = [1, 2; //node = [ i, j]
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
parameter Integer n = 4; //jumlah node
parameter Integer [:] Boundary_xyz = {1}; //titik pada node
parameter Integer [:] Boundary_xy = {4};
parameter Integer [:] Boundary_xz = {0};
parameter Integer [:] Boundary_yz = {0};
parameter Integer [:] Boundary_x = {3};
parameter Integer [:] Boundary_y = {0};
parameter Integer [:] Boundary_z = {0};
parameter Real [3*n] load = {0, 0, 0, //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L;
Real [size(inisiasi,1)] k;
Real [size(inisiasi,1),6,6] Ke;
Real [size(inisiasi,1),3*n,3*n] Kg;
Real [3*n,3*n] KgTot;
Real [3*n,3*n] KgB;
Real [3*n] U;
Real [3*n] R;
Real [3] F;
equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(n, node, Ke);
KgTot = SumStiffnessMatrixGlobal(Kg);
KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);
U = GaussJordan(KgB, load);
R = ReactionForce(KgTot, U, load);
F = CheckForce(load,R);
end spacetruss; |
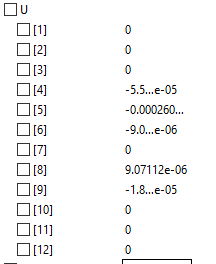
Hasil Displacement
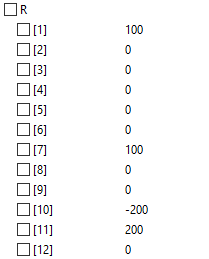
Hasil Gaya Reaksi Hasil Total Gaya |
Pertemuan 6: Senin, 14 Desember 2020
Pada pertemuan ini, kami melakukan muhasabah diri terkait pemahaman kami terhadap aplikasi metode numerik. Berikut muhasabah diri saya:
Menurut saya, selama mengikuti mata perkuliahan ini, saya sudah cukup memahami materi yang diberikan sebelum UTS. Materi tersebut menjadi acuan untuk mengerjakan soal-soal atau permasalahan menggunakan aplikasi Openmodelica yang dilaksanakan setelah UTS. Dalam pengerjaannya, kita harus tahu hubungan antara model matematis, model numerik, dan komputer sebelum disimulasikan. Penelesaian-penyelesaian tersebut terbantu oleh metode numerik dengan menggunakan Openmodelica. Kami telah berhasil menyelesaikan defleksi pada batang dengan menggunakan code, sesuai modul yang diberikan. Tahapan-tahapan yang dilakukan yaitu analisis parameter dan masalah terlebih dahulu, membuat flowchart, dan membuat model numerik berupa code dari flowchart tersebut. Dalam memahami pembelajaran ini, saya sudah cukup paham mengenai code yang digunakan dan pengaplikasiannya, namun masih kesulitan dalam membuat code dari permasalahan yang diberikan dan harus belajar lagi tentang fungsi-fungsi yang ada di bahasa modelica.
Pertemuan 7: Senin, 21 Desember 2020
Pada pertemuan ini, kami melakukan praktek aplikasi metode numerik dalam kasus optimasi. Pak Dai pertama-tama menjelaskan pada truss ada 3 derajat kebebasan, yaitu x, y, z. Sedangkan beam terdapat 6 derajat kebebasan, yaitu x, y, z, dan momen yaitu theta, r, x. Pada penyelesaian tugas besar ini, kita asumsikan sebagai truss. Tujuan dari tugas besar ini adalah untuk menekan biaya dalam desaun yang digunakan. Optimasi ini mencari gaya dan kesetimbangan gaya. Dalam perhitungannya mencari stress, dann bandingkan dengan kekuatan material. Tegangan yang terjadi tidak boleh melebihi 1/2 kekuatannya.
Kemudian kita harus menentukan jenis material yang digunakan, seperti stainless steel. Setelah itu identifikasi dimensi yang digunakan, biaya yang dikeluarkan, spesifikasi, dan perbandingannya dengan material lain.
Tugas Besar Metode Numerik
Brikut pembahasan tugas besar metode numerik yang saya kerjakan:
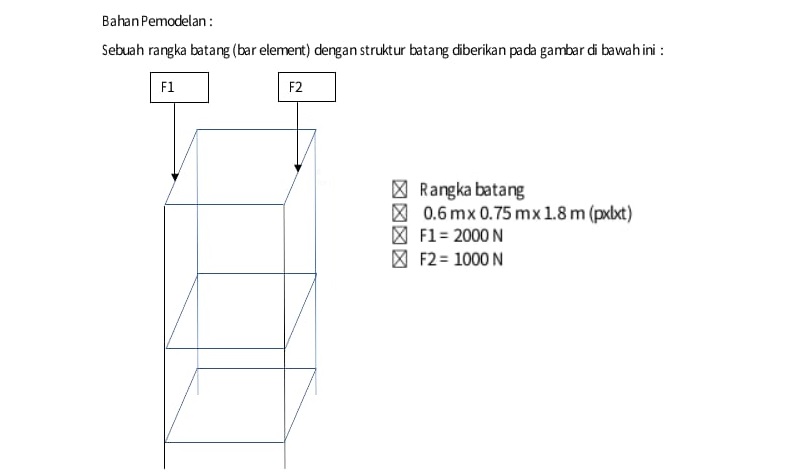
Pada tugas besar ini, kami persoalan dengan objektif mengoptimasi harga pembuatan rangka truss sederhana dengan variasi dimensi dan elastisitas material.
Diketahui:
- F1=2000 N
- F2=1000 N
- spesifikasi truss
- geometri truss
Asumsi yang diberikan:
- variasi stiffness terkait dengan material yang digunakan
- beban terdistribusi pada node (karena trusses)
- safety factor bernilai 2
- batas displacement 0,001 m sebelum buckling
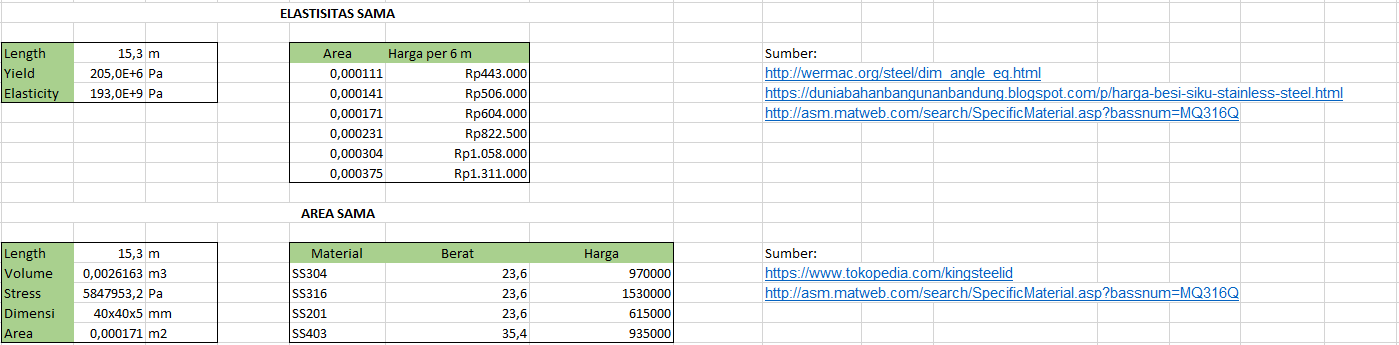
Data yang digunakan:
Pada bagian dengan elastisitas yang sama, saya menggunakan material AISI Type 316L Stainless Steel (SS316L) dengan variasi area. Sementara pada bagian Area sama, saya menggunakan 6 sampel material yaitu SS304, SS316, SS201, dan SS403.
Kode yang digunakan
Perhitungan displacement, reaction force, dan stress:
Model Trusses 3D
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety; |
Curve fitting untuk menemukan nilai terhadap data yang sudah ada:
Class curve fitting
class curvefitting
parameter Real X[:]={1109363,1109363,531152,538341}; //input variabel x
parameter Real Y[:]={290e6,290e6,379e6,275e6}; //input variabel y
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end curvefitting; |
Fungsi panggil curve fitting
function Curve_Fitting
input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];
protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);
A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);
end Curve_Fitting; |
Perhitungan Golden section method untuk optimasi
Golden Section
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold; |
Hasil Perhitungan
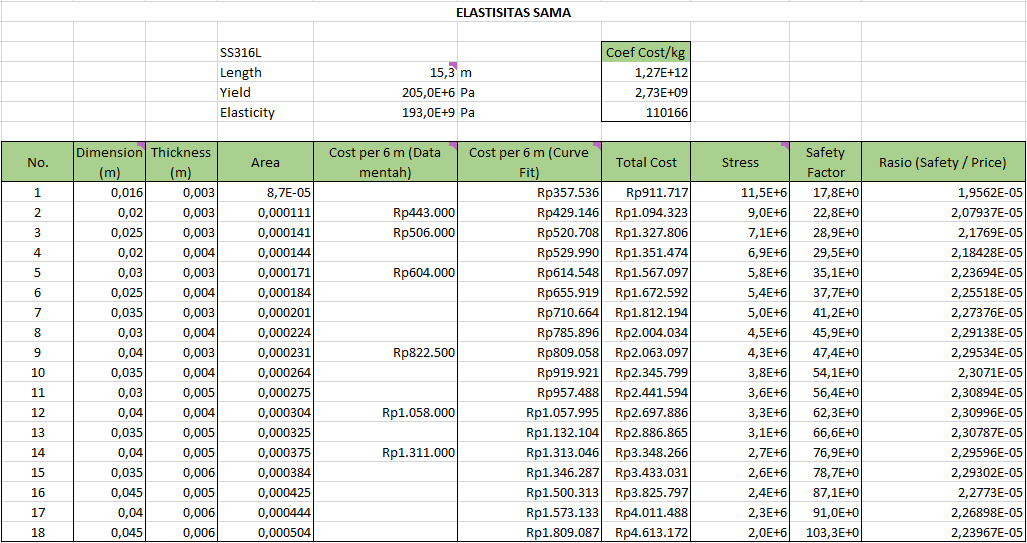
Berikut adalah hasil perhitungan nilai rasio safety factor dengan harga total. Pada elastisitas sama, untuk mencari harga lain yang tidak ada pada sampel saya melakukan curve fitting sehingga harga-harga lainnya dapat diketahui. Nilai stress didapatkan dari aplikasi openmodelica. Pada bagian area yang sama dilakukan curve fitting pada bagian cost per kg, density, dan yield.
1) Elastisitas Sama
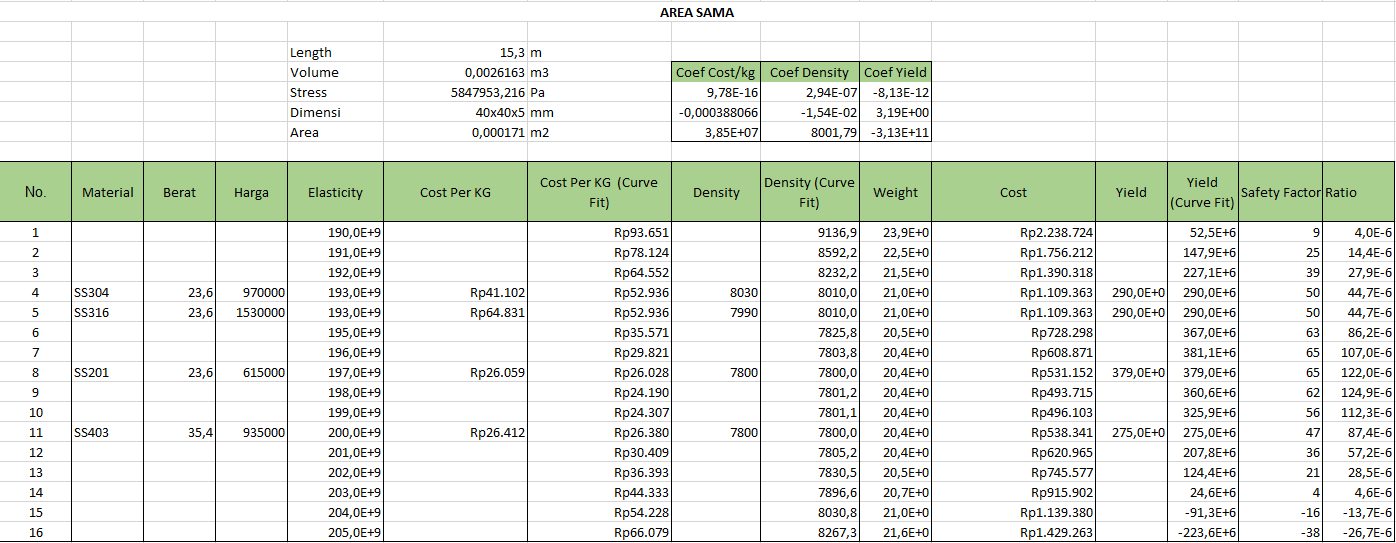
2) Area Sama
Setelah ditemukan rasio masing-masing data, kemudian dilakukan optimasi dengan metode golden ratio. Berikut hasil dari optimasi tersebut:
1) Elastisitas Sama
Pada kasus elastisitas sama, nilai luas area penampang optimum untuk material SS316L adalah 219mm^2. Jika melihat tabel di atas, maka batang paling optimum dengan dimensi 30 mm dengan tebal 4mm.
2) Area Sama Pada kasus area sama, material paling optimum untuk luas penampang 171mm^2 adalah material dengan elastisitas 1.97e^11 N/m^2 sehingga batang paling optimum yaitu SS201.
UJIAN AKHIR SEMESTER
Berikut jawaban UAS Metode Numerik yang diadakan pada hari Rabu, 13 Januari 2020.
1. Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut.
- membuat desain dasar bangunan yang diamati
- menentukan variabel/parameter yang dihitung misalnya dimensi, harga, material
- membuat perhitungan numerik untuk mencari safety factor yaitu yield material dibagi stress bangunan
- memvariasikan data dengan luas material tetap dan elastisitas material tetap
- melakukan curve fitting untuk menccari data-data lainnya
- setelah data ditemukan, mencari rasio safety factor dengan variabel yang divariasikan, area untuk area tetap dan elastisitas untuk elastisitas tetap
- melakukan optimasi dengan menggunakan powell method sehingga didapatkan nilai paling optimum
2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan!
- tujuan pemodelan: mendapatkan struktur dengan material dan harga yang paling optimal pada water tower sehingga biaya dapat ditekan dan tetap dapat menahan struktur yang ada.
- hukum fisika: statika struktur, stress, strain, hukum hooke, dan konstanta kekakuan
- asumsi: beban material diabaikan, struktur berupa trusses, struktur statis
3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D).
a)Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal)
b)Matriks kesetimbangan global
- persamaan aljabar -> Fn=k*∆x. Rumus ini diturunkan menjadi:
R-K1(U2-U1)=0 K1(U2-U1)-K2(U3-U2)=0 K2(U3-U2)-F=0
- matriks keseimbangan global -> [K]*{X}={F}. Rumus ini, diturunkan menjadi:
[K, -K1, 0; [U1; [-R1, -K1,K1+K2,-K2; * U2; = 0 0, -K2, K2+K3] U3] F]
4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya
- input parameter yang diperlukan(A,E,L,load)
- mencari konstanta kekakuan (k=AE/L)
- menyelesaikan matriks kekakuan elemen
- transformasi matriks elemen ke matriks global [K]g
- menjumlahkan matriks global total
- menerapkan boundary condition pada matriks global
- menyelesaikan displacement dari matriks global, force, dan boundary {X}=[K]^-1*{F}
5. Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut!
- fungsi objektif: untuk mencari stress pada water tower berdasarkan data yang diketahui
- constraint
- beban = 30.000 galon
- tinggi = 120 feet
6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas!
- V = 30.000 galon -> 249866 lb
- F = 249866 lb * 32,1740 ft/s^2 = 803918,6 lbf
- A = 20 in^2
- h = 120 ft
- E = 10^7 lb/in^2
- k = A*E/h = 20*10^7/120=166,7*10^4
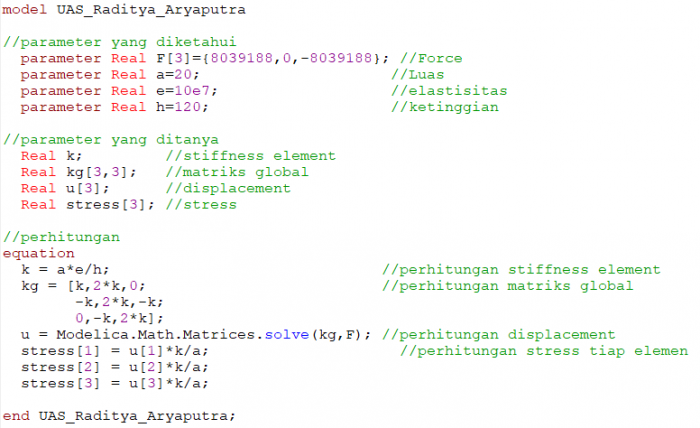
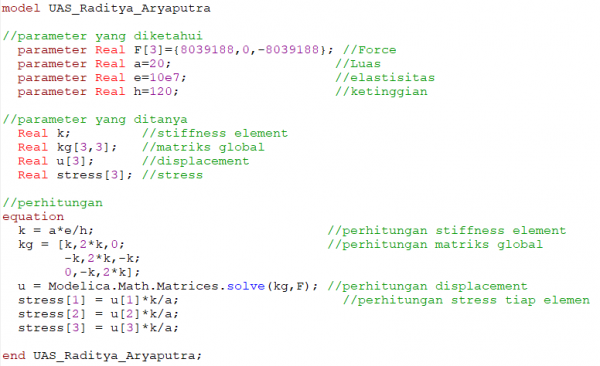
7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6!
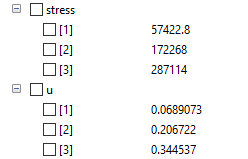
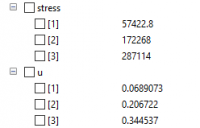
Hasil dari perhitungan ini adalah
- stress 1 = 57422,8 lbf/in^2
- stress 2 = 172268 lbf/in^2
- stress 3 = 287114 lbf/in^2
- displacement 1 = 0.06 ft
- displacement 2 = 0.02 ft
- displacement 1 = 0.03 ft
Lampiran Foto Progress