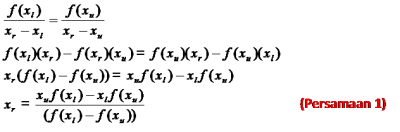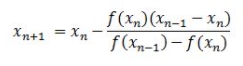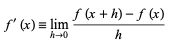Metnum03-Mizan Eryandhika Guntorozi
Contents
Pendahuluan
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan, nama saya Mizan Eryandhika Guntorozi atau yang biasa dipanggil Mizan, saya merupakan mahasiswa S1 Paralel Teknik Mesin Universitas Indonesia. Berikut adalah biodata diri saya dan juga catatan-catatan saya mengenai Perkuliahan Jarak Jauh(PJJ) mata kuliah Metode Numerik sampai dengan Ujian Akhir Semester(UAS). Catatan tersebut meliputi tugas yang diberikan pada setiap pertemuan juga progress pembelajaran saya setiap diadakan pertemuan. Saya berharap page ini dapat memberikan manfaat bagi siapapun yang membaca. Terimakasih.
Pertemuan 1: 9 November 2020
Pada pertemuan kali ini, Pak Dai meminta mahasiswa untuk bisa aktif berdiskusi selama pembelajaran, juga pada pertemuan kali ini mahasiswa ditekankan untuk tetap terus belajar dan bisa mengaplikasikan teknologi untuk membantu pembelajaran, pada mata kuliah metode numerik ini aplikasi yang diharapkan untuk bisa dikuasai mahasiswa adalah aplikasi Open Modelica.
Materi sebelum UTS
Pada saat sebelum UTS, perkuliahan metoda numerik yang diajar oleh Pak Engkos dengan referensi buku Numerical Method For Engineers oleh Steven Chapra meliputi beberapa bahasan seperti berikut:
1. Truncation error
Truncation error merupakan error yang terjadi karena pemotongan dari suatu deret tak hingga menjadi deret berhingga. Pendekatan yang sering dipakai pada penyelesaian numerik adalah deret taylor. Untuk menyederhanakan permasalahan biasanya perhatian hanya ditujukan pada beberapa suku dari deret taylor tersebut, sedangkan suku lainnya diabaikan. Pengabaian suku inilah yang menyebabkan truncation error. Deret taylor sendiri merupakan dasar untuk menyelesaikan masalah dalam metode numerik, terutama penyelesaian persamaan diferensial. Jika fungsi f(x) diketahui di titik xi dan semua turunan dari f terhadap x diketahui pada titik tersebut. Dengan deret Taylor dapat dinyatakan nilai f pada titik xi+1 yang terletak pada jarak Dx dari titik xi.
Truncation error terjadi ketika suatu rumus komputasi disederhanakan dengan cara membuang suku yang berderajat tinggi. Sebagai contoh nilai cosinus (cos(x)) dapat didekati dengan deret Taylor, sebagai berikut:
cos(x) = 1 – x2/2! + x4/4! – x6/6! + x8/8! – x10/10! + …
misalkan x=1.5, maka nilai eksak cos(1.5) = 0.070737, namun jika cos(1.5) dihitung menurut deret Taylor hingga suku ke-4 saja, maka:
cos(1.5) = 1 – (1.5)2/2! + (1.5)4/4! – (1.5)6/6! = 0.070187
dengan demikian ada kesalahan sebesar 0.000550 dari nilai sebenarnya akibat adanya “truncation” atau pemotongan.
2. Roots of Equation - Bracketing Method dan Open Method
Bracketing Method: Metode ini adalah suatu metode dalam metode numerik yang berfungsi untuk mencari akar-akar dari suatu persamaan dengan cara menebak dua nilai,kemudian kita mengurung dengan menggunakan kedua nilai tersebut hingga kita dapat menemukan akar-akar dari persamaan tersebut.
a) Metode Bisection
Akar-akar persamaan pada metode bisection memiliki persyaratan sebagai berikut:
f(xl).f(xu) < 0,
yang artinya:
Akan ada paling sedikit satu akar persamaan diantara xl dan xu. xl adalah x di bawah, xu adalah x di atas.
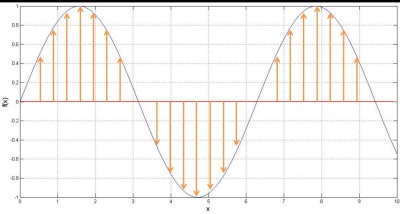
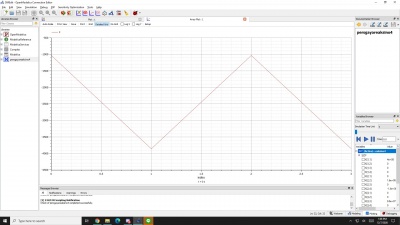
Metode bisection digunakan dalam mencari akar persamaan yang dilakukan dengan cara membagi dua setiap interval yang ada. Posisi akar persamaan dapat ditentukan dengan cara melihat perubahan tanda pada gelombang yang terjadi. Contohnya seperti grafik di bawah:
Terlihat saat perubahan tanda (arah panah berubah) maka akan ada paling sedikit satu akar persamaan. Pada contoh di atas f(x) = sinx, terlihat ada sekitar empat akar persamaan yaitu saat x = 0, x = π, x = 2 π, x = 3 π.
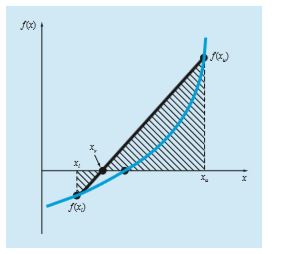
b) Metode False position
Jika f(xl) dan f(xu) dihubungkan dengan garis lurus, perpotongan garis dengan sumbu x menunjukkan adanya akar pendekatan (estimate of root). Seperti gambar di bawah ini:
Pada metode ini nilai xr juga dapat digunakan prinsip persamaan di bawah ini:
Setelah nilai xr didapat, kemudian xr menggantikan nilai tebakan awal xl atau xu, dengan cara ini nilai xl dan xu akan selalu mengurung nilai akar. Cara ini dilakukan terus sampai menemukan akar dengan error yang diinginkan.
Open Method: Metode ini adalah metode yang didasarkan pada formula yang hanya membutuhkan nilai awal tunggal x atau dua nilai. Berbeda dengan Metode Bracketing yang perhitungannya menggunakan perkiraan yang lebih dekat dari nilai sebenarnya dari akar dan yang dikatakan konvergen.
a) Metode Iterasi Sederhana (Simple Fixed-Point Iteration Method)
Metode terbuka menggunakan rumus untuk memprediksi akar. Formula seperti itu dapat dikembangkan untuk Simple Fixed-Point Iteration Method (atau, seperti yang juga disebut, satu titik iterasi atau substitusi berturut-turut) dengan mengatur kembali fungsi f(x) = 0 sehingga x ada di sisi kiri persamaan. Seperti contoh sebagai berikut ini:
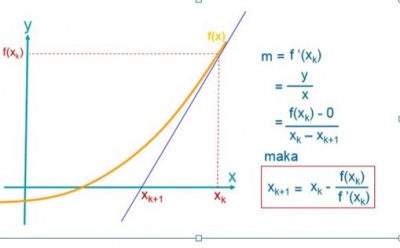
b) Metode Newton-Rapshon
Metode Newton-Raphson merupakan salah satu metode terbuka untuk menentukan solusi akar dari persamaan non linier, dengan prinsip utama sebagai berikut:
-Metode ini melakukan pendekatan terhadap kurva f(x) dengan garis singgung (gradien) pada suatu titik awal
-Nilai taksiran selanjutnya adalah titik potong antara garis singgung (gradien) kurva dengan sumbu x
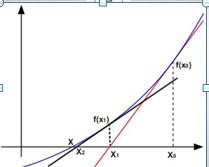
c) Metode Secant
Pada Metode Newton-Raphson memerlukan syarat wajib yaitu fungsi f(x) harus memiliki turunan f’(x). Sehingga syarat wajib ini dianggap sulit karena tidak semua fungsi bisa dengan mudah mencari turunannya. Oleh karena itu muncul ide dari yaitu mencari persamaan yang equivalent dengan rumus turunan fungsi. Ide ini lebih dikenal dengan nama Metode Secant. Ide dari metode ini yaitu menggunakan gradien garis yang melalui titik (x0, f(x0)) dan (x1, f(x1)). Dengan contoh seperti di bawah ini:
3. Gauss Elimination
Metode Eliminasi gauss dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan merepresentasikan (mengubah) menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk Eselon Baris melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik.
4. Curve Fitting
Metode pencocokan kurva dapat dilakukan dengan melakukan regresi linear.
5. Numerical Differentiation
Numerical Differentiation adalah proses menemukan nilai numerik dari turunan fungsi tertentu pada titik tertentu. Seperti contoh di bawah ini:
- dengan catatan h<1 .
Kemudian, Pak Dai memicu diskusi untuk membahas pengaplikasian metode numerik yang sudah lalu pada saat sebelum UTS untuk mahasiswa menceritakan apa saja yang bisa diambil dari materi-materi yang sudah dipelajari sebelumnya, pada kehidupan sehari-hari terutama. Kemudian, Pak Dai mengharapkan untuk setiap mahasiswa dapat menjelaskannya di youtube channel masing-masing mengenai hal tersebut, dan juga tambahan untuk mempelajari aplikasi Open Modelica tadi untuk kemudian dijelaskan di masing-masing video youtube mahasiswa. Berikut adalah tautan hasil tugas saya berupa link video youtube mengenai hal tersebut:
Tugas 1: https://youtu.be/n5r8cb-cfQc
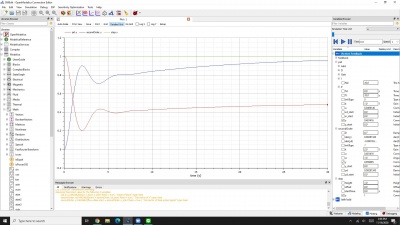
Berikut adalah bentuk model yang saya buat yaitu model sistem pid feedback control
Kemudian di bawah ini adalah hasil grafik yang muncul setelah dilakukan simulasi:
Pertemuan 2: 16 November 2020
Pada pertemuan kali ini, Pak Dai memberikan materi mengenai bahasa Open Modelica yang bisa kita praktikkan sendiri-sendiri. Materi yang diberikan yaitu membuat suatu persamaan yang bisa dipecahkan dengan menggunakan bahasa Open Modelica.
Pak Dai memberikan para mahasiswa 2 bentuk latihan yaitu:
1. Latihan pertama - Bentuk lathan yang pertama memecahkan atau menentukan suatu nilai variabel x atau y didalam satu persamaan dengan menggunakan bahasa Open Modelica itu sendiri.
Bentuk latihan pertama yang diberikan kurang lebih seperti ini:
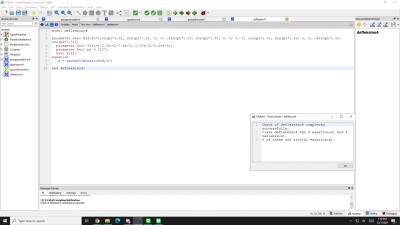
Di bawah ini adalah bahasa open modelica yang digunakan dan rangkaiannya untuk memecahkan atau menentukan nilai variabel x atau y, caranya adalah langkah pertama yaitu membuat new modelica class dengan spesialisasi bagan "class" dan membuat persamaannya dengan bahasa open modelica seperti gambar di bawah ini:
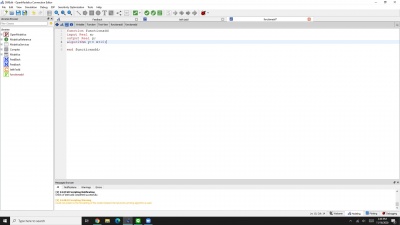
Kemudian seperti terlihat pada gambar, ada bahasa open modelica yang bertuliskan "functionadd", sebenarnya bahasa "functionadd" ini bertujuan untuk menyambungkan kedua modelica class yang berbeda. "functionadd" disini juga harus sesuai dengan nama file yang kita buat di spesialisasi modelica class function itu sendiri agar bisa terangkai atau tersambung bahasa open modelica tersebut untuk kemudian disimulasikan menjadi satu kesatuan. "functionadd" itu sendiri berbunyi seperti gambar di bawah ini yang berisikan fungsi yang ingin dipecahkan.
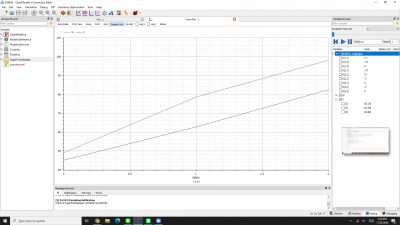
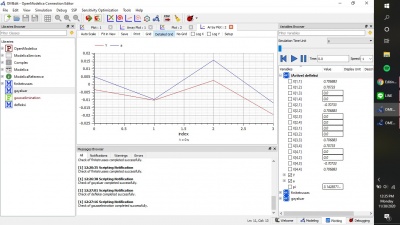
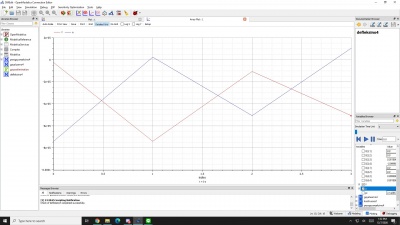
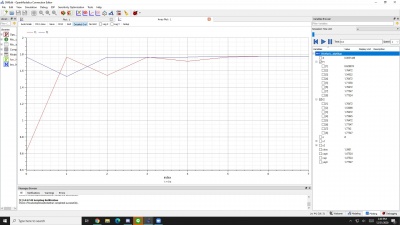
Kemudian setelah disimulasikan, muncul hasil seperti grafik di bawah di bagian plotting, sehingga kita tahu nilai dari x dan y tersebut yang ada di sebelah kanan gambar, seperti gambar di bawah ini.
2. Latihan kedua - Bentuk lathan yang kedua, mahasiswa diharapkan merangkai bahasa open modelica sendiri untuk mencari mean dari persamaan yang dibuat juga sendiri oleh masing-masing mahasiswa.
Bentuk latihan kedua yang saya simulasikan kurang lebih seperti ini:
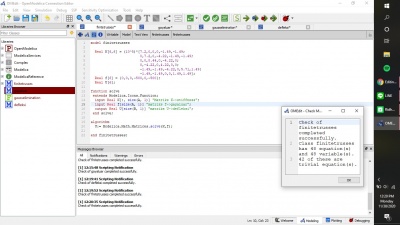
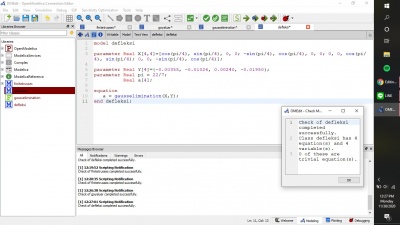
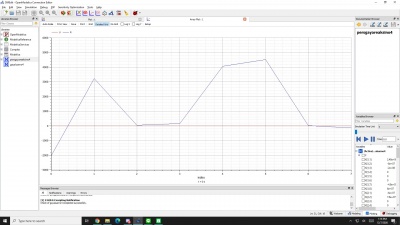
Langkah pertama yang dilakukan adalah merangkai persamaan data yang ingin dicari mean nya, disini saya menggunakan 12 data random untuk mencari rata-rata atau mean dari ke-12 data seperti gambar di bawah ini. Gambar di bawah ini adalah bahasa open modelica yang bisa digunakan untuk mencari mean. Kemudian langkah kedua adalah melakukan check dan dari model class yang saya buat, terdapat 1 persamaan serta 1 variabel dan proses check nya menunjukkan tidak ada masalah sehingga dapat dilanjutkan kepada proses selanjutnya.
Proses selanjutnya adalah melakukan simulasi dengan mengklik tanda panah hijau diatas dan akan muncul tab seperti dibawah ini menunjukkan bahwa proses simulasi sedang berlangsung
Lalu, setelah itu muncul grafik beserta hasil mean di bagian plotting yang telah dilalui proses perhitungan menggunakan aplikasi open modelica ini, seperti pada gambar di bawah ini:
Tugas 2 - Tugas memecahkan suatu persamaan aljabar simultan.
Aljabar simultan adalah metode penyelesaian persoalan matematik yang melibatkan kekompleksan yang sangat rumit sehingga membutuhkan bantuan software seperti OpenModelica. Berikut adalah jenis-jenis metode yang dapat diselesaikan dengan cara aljabar simultan:
1. Eliminasi Gauss; 2. Cramer; 3. Gauss Seidel; 4. Gauss Jordan
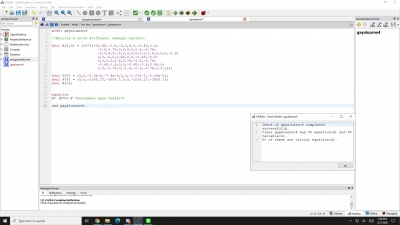
Pada tugas ini saya mencoba menyelesaikan akar-akar dari persamaan gauss elimination. Berikut adalah persamaan gauss elimination yang saya gunakan: x+y+z=3; 2x+3y+7z=0; x+3y-2z=17
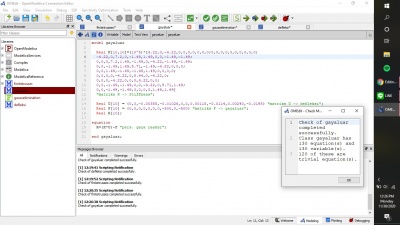
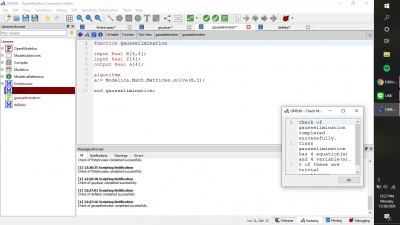
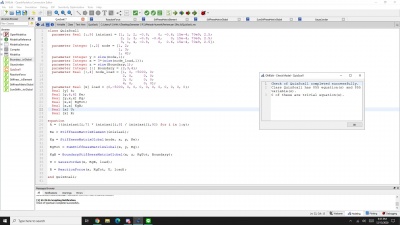
Langkah pertama yang saya lakukan adalah membuat modelica class baru tipe class dan membuat fungsi-fungsi dan variabel seperti Real A[3,3] dimana 3,3 menunjukkan matriks yang digunakan adalah matriks orde 3x3 dan parameter real B[3] dimana angka 3 menunjukkan matriks dengan orde 3x1 serta terakhir adalah parameter X dimana X yang akan dicari 3 akar-akarnya setelah dilakukan simulasi. Kemudian, saya membuat modelica class tipe function dengan berisikan fungsi yang akan digunakan untuk menyelesaikan persamaan. Gambar berikut adalah hasil rangkaian bahasa modelica yang sudah di cek dengan berisikan 15 persamaan dan 15 variabel yang sudah oke.
Selanjutnya, berikut adalah setting simulasi yang saya lakukan
Langkah selanjutnya adalah proses simulasi seperti gambar berikut
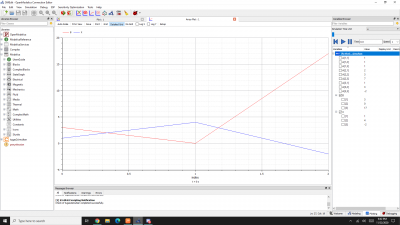
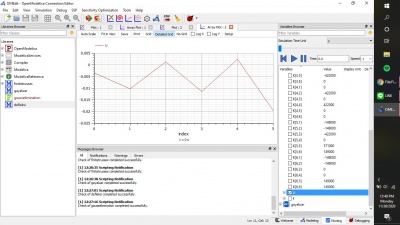
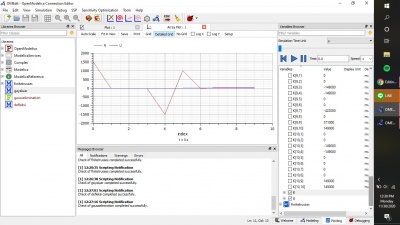
Setelah dilakukan simulasi, didapatkan akar-akar dari persamaan gauss elimination tadi yaitu X1=1 ; X2=4 ; X3=-2. Berikut adalah hasil simulasinya
Pertemuan 3: 23 November 2020
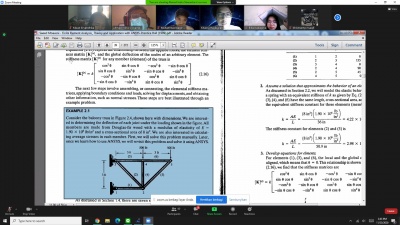
Pada pertemuan kali ini, Pak Dai memaparkan aplikasi metode numerik dalam permasalahan teknik yang bersumber dari buku Numerical Methods for Engineers 7th edition chapter 12.4 Spring-Mass Systems karya Steven Chapra.
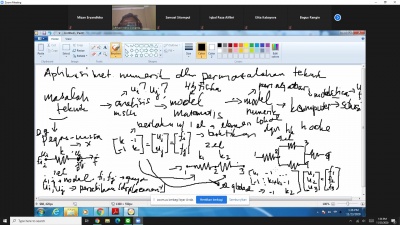
Kemudian, Pak Dai menjelaskan terdapat beberapa langkah yang dapat membantu untuk kita dapat memecahkan masalah keteknikan yaitu dengan proses sebagai berikut:
1. Masalah Teknik - masalah teknik yang dijadikan acuan adalah pegas massa dengan persamaan, mencari respon pada sistem dan juga bagaimana peralihan/displacement pada titik yang kita tentukan ada masalah kita teliti 2. Analisis Masalah - dari analisis masalah kita dapatkan pertanyaan atau studi kasus 3. Model Matematis - dilakukan model matematis dengan hukum fisika 4. Model Numerik - dari hukum fisika kita dapat turunkan menjadi model numeriknnya 5. Komputer - ditranslasikan dengan software komputer dalam hal ini adalah OpenModelica 6. Solusi - ketemu solusi (u,f)
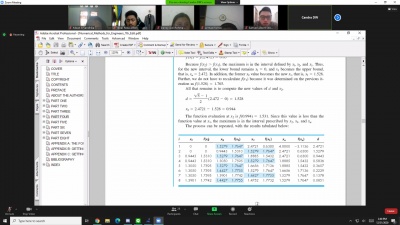
Matriks lokal seperti yang dapat di lihat di gambar atas berlaku untuk model contoh massa pegas 1 elemen, berikutnya Pak Dai memberikan contoh massa pegas yang lainnya yaitu yang mempunyai 2 dan 4 elemen. Matriks lokal yang tadi hanya berlaku untuk massa pegas 1 elemen saja, untuk matriks 3x3 yang disampingnya itu merupakan permodelan yang berlaku untuk massa pegas 2 elemen yang didapatkan dengan cara menurunkan matriks lokal tadi dan digabungkan menjadi 2 matriks lokal menjadi matriks global. Terlihat untuk massa pegas yang berbeda elemennya, terdapat perbedaan pula pada hasil akhir displacement yang didapatkan.
Latihan - Latihan ini untuk mensimulasikan matriks dengan masalah keteknikan sehari hari yaitu massa pegas.
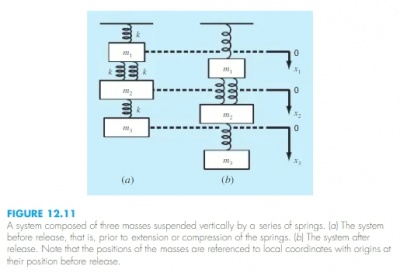
Pak Dai dikelas memberikan studi kasus dari buku di gambar 12.11. Pak Dai meminta mahasiswa untuk bisa membuktikan persamaan aljabarnya dan diselesaikan dengan OpenModelica. Berikut adalah contoh massa pegas yang di minta Pak Dai untuk para mahasiswa bisa membuktikan matriks lokal dan global dengan massa pegas beberapa elemen.
1. Pembuktian dan hasil matriks global
2. Simulasi penyelesaian pada OpenModelica
Setelah itu, dilakukan simulasi terkait persamaan matriks dengan contoh massa pegas diatas, berikut adalah persamaan dan matriks yang saya gunakan untuk dilakukan simulasi menggunakan OpenModelica:
// Berikut adalah Rumus [K]{X}={W}
// [K] = [3k,-2k,0
// -2k,3k,-k;
// 0,-k,k];
// {W} = {m1g,m2g,m3g};
// Dimana k yang saya gunakan untuk masing-masing elemen adalah k=5kg/s^2; m1=5kg; m2=8kg; m3=10kg; g=9.81;
// Persamaan Matriks Baru
// [K] = [15,-10,0;
// -10,15,-5;
// 0,-5,5];
// {W} = {49.05,78.48,98.1};
Sama seperti sebelum-sebelumnya, langkah pertama yang saya lakukan adalah membuat modelica class baru tipe class dan membuat fungsi-fungsi dan variabel seperti Real A[3,3] dimana 3,3 menunjukkan matriks yang digunakan adalah matriks orde 3x3 dan parameter real B[3] dimana angka 3 menunjukkan matriks dengan orde 3x1 serta terakhir adalah parameter X dimana X yang akan dicari 3 akar-akarnya setelah dilakukan simulasi. Kemudian, saya membuat modelica class tipe function dengan berisikan fungsi yang akan digunakan untuk menyelesaikan persamaan. Terdapat 15 persamaan dan 15 variabel yang sudah oke seperti dibawah ini
Selanjutnya, berikut adalah setting simulasi yang saya lakukan:
Langkah selanjutnya adalah proses simulasi seperti gambar berikut
Setelah dilakukan simulasi, didapatkan displacement X tadi yaitu X1=45.126 ; X2=62.784 ; X3=82.404. Berikut adalah hasil simulasinya
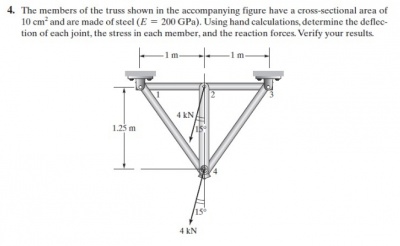
Tugas 3 - Tugas pada kali ini adalah menentukan titik reaksi displacement pada setiap joint dan gaya-gaya reaksinya.
Tugas pada kali ini adalah melakukan studi kasus di buku pada gambar 11.12. Kemudian membuktikan persamaan aljabarnya dan disimulasikan dengan OpenModelica.
Berikut adalah langkah-langkah pembahasan soal finite element analysis dari sumber buku Numerical Methods for Engineers 7th edition.
Gambar di bawah ini adalah persamaan matriks lokal yang kemudian di gabungkan menjadi persamaan matriks global untuk menyelesaikan persamaan
Kemudian di bawah ini adalah gambar penjabaran trusses yang ada pada setiap rangka batang yang ada pada soal
Selanjutnya, di bawah ini adalah menyatukan elemen daripada rangka batang yang sudah dijabarkan sebelumnya
Gambar di bawah ini adalah kita menentukan boundary condition yang ada pada sistem tersebut dan menentukan variabel-variabel seperti load pada sistem
Gambar selanjutnya adalah solusi yang didapatkan yang kemudian akan disimulasikan pada aplikasi OpenModelica
Berikut ini adalah screenshot hasil kerja saya yang saya simulasi kan pada aplikasi OpenModelica menggunakan finite element stress analysis.
Hasil simulasi:
Pertemuan 4: 30 November 2020
Perbedaan pendekatan statik dan dinamik:
Statik terstruktur adalah membahas respon benda atau material dari beban yang statis artinya beban yang diam atau hanya menunjukkan gaya-gaya reaksi, sigma F = 0 atau tetap. Intinya sepanjang waktu bebannya tetap. Tidak berubah terhadap waktu.
Dinamis adalah membahas respon benda atau material dari beban yang dinamis artinya ada perubahan gerak pada beban tersebut, sigma F ditandai adanya perubahan kecepatan artinya sigma F tidak sama dengan 0. Bebannya bisa mengalami penambahan ataupun pengurangan terhadap waktu. Ada variabel berubah terhadap waktu seperti angin atau gempa.
Selanjutnya, kelas dilanjutkan dengan diskusi yang di pimpin oleh Pak Dai, untuk membahas latihan tugas yang minggu lalu telah diberikan. Dari diskusi yang telah dilakukan oleh mahasiswa dan Pak Dai dapat di ambil kesimpulan bahwa persoalan yang telah diberikan sebelumnya diharapkan dapat membantu mahasiswa. Aplikasi metode numerik pada masalah keteknikan dapat membantu mahasiswa menyelesaikan persoalan tersebut. Berikut bunyi nya:
1. Masalah Teknik - masalah teknik yang dijadikan acuan adalah struktur finite element pada batang dengan persamaan, mencari node dan elemen pada masing-masing titik 2. Analisis Masalah - dari analisis masalah kita dapatkan pertanyaan atau studi kasus 3. Model Matematis - dilakukan model matematis dengan hukum fisika 4. Model Numerik - dari hukum fisika kita dapat turunkan menjadi model numeriknya 5. Komputer - ditranslasikan dengan software komputer dalam hal ini adalah OpenModelica 6. Solusi - ketemu solusi displacement ataupun gaya reaksi (U,F)
Dari langkah-langkah tersebut Pak Dai memberikan tugas untuk latihan kepada para mahasiswa agar dapat mencoba memahami penggunaan aplikasi OpenModelica untuk diterapkan untuk menyelesaikan masalah keteknikan. Kemudian dari diskusi tersebut dilanjutkan oleh Pak Dai memberi tugas latihan tentang struktur batang yang lain dan dijadikan KUIS.
KUIS: Membuat Design Flowchart untuk dapat menyelesaikan masalah keteknikan untuk selanjutnya disimulasikan dengan bahasa OpenModelica.
Berikut ini adalah soal yang diberikan Pak Dai. Contoh soal nomor 4 dan 8:
Kuis ini dapat diselesaikan dengan langkah awal membuat flowchart, untuk kemudian dapat membantu mahasiswa memecahkan permasalahan atau persoalan keteknikan seperti soal diatas. Berikut adalah hasil kerja flowchart yang saya kerjakan. Berikut adalah hasil kerja flowchart saya:
Jawaban Kuis Nomor 4
Berikut adalah hasil OpenModelica yang saya kerjakan. Untuk tahapan pengerjaannya, saya mengacu pada flowchart di atas yang telah saya kerjakan. Kurang lebihnya langkah yang saya lakukan adalah seperti ini.
1. Langkah pertama adalah untuk menentukan matriks global yang akan berlaku dan digunakan pada persoalan nomor 4 dengan cara menurunkan matriks lokal pada setiap joint di persoalan nomor 4 ini. 2. Langkah kedua adalah dari matriks global yang ditemukan tadi, kita lakukan simulasi dengan menggunakan aplikasi OpenModelica 3. Langkah ketiga, dengan adanya variabel-variabel yang ada, kita dapat menemukan variabel yang dibutuhkan, dalam hal ini adalah variabel defleksi (U) serta variabel konstanta kekakuan(K) pada setiap elemen (sudah diketahui E=200 GPa, luas permukaan (A) = 10^-3m2 dan panjang batang untuk 3 variasi yaitu untuk 1m, 1,25m, dan 1,6m) 4. Langkah keempat, dengan didapatkannya variabel defleksi dan konstanta kekakuan batang, kita dapat menemukan persamaan gaya reaksi yang terjadi dengan rumus R=(K*U)-F 5. Langkah kelima, mensimulasikan dengan menggunakan aplikasi OpenModelica untuk mendapatkan hasil reaction force atau gaya reaksi pada setiap elemen.
Gambar-gambar di bawah ini adalah hasil simulasi dan screenshot bahasa modelica yang saya gunakan untuk menyelesaikan persoalan kuis nomor 4 ini:
Pertemuan 5: 7 Desember 2020
Pada pertemuan kali ini, di pimpin oleh Pak Dai untuk berdiskusi tentang tahap-tahap dalam menyelesaikan soal-soal pada kuis yang diberikan minggu lalu.
Kemudian, pertemuan ini dilanjutkan oleh Ahmad Mohammad Fahmi yang kemudian menjelaskan mengenai flowchart yang ia buat sendiri walaupun belum mengaplikasikan hitung-hitungannnya. Ahmad ini kemudian menjelaskan bahasa Modelica yang ia gunakan untuk menyelesaikan permasalahan yang ada pada kuis nomor 4 dan 8. Disini saya mempelajari hal-hal baru karena Saudara Ahmad menggunakan bahasa Modelica yang jarang saya dengar, contohnnya saya baru mengetahui cara looping pada aplikasi OpenModelica. Saudara Ahmad ini juga menyelesaikan persoalan dengan runtut sehingga mudah dibaca dan untuk diaplikasikan kemudian.
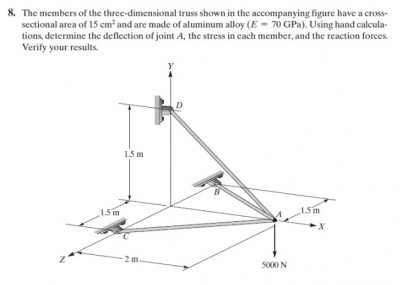
Berikut adalah hasil OpenModelica yang baru saya pelajari untuk menyelesaikan persoalan kuis minggu lalu nomor 8. Untuk tahapan pengerjaannya, saya mengacu pada flowchart di atas yang telah saya kerjakan. Kurang lebihnya langkah yang saya lakukan adalah seperti ini.
1. Langkah pertama adalah untuk menentukan matriks global yang akan berlaku dan digunakan pada persoalan nomor 8 dengan cara menurunkan matriks lokal pada setiap joint di persoalan nomor 8 ini. Pada soal nomor 8 ini digunakan rumus k= A.E/L kemudian dari situ berangkat ke Ke yaitu K pada setiap elemen yang kemudian baru kita tentukan dari Ke ke Kg yaitu K pada matriks global setiap elemen tadi, lalu ditambahkan sehingga kita dapatkan KgTot, tentunya pada penyelesaian kita masukkan function Boundary pada Kg untuk menambahkan looping pada setiap dimensi karena persoalan kali ini digunakan 3 dimensi. Namun, berbeda dengan nomor 4, variabel yang digunakan pada soal nomor 8 ini theta nya harus dibagi 3 per dimensi x,y,z karena 3 dimensi. 2. Langkah kedua adalah dari matriks global total yang ditemukan tadi, kita lakukan simulasi dengan menggunakan aplikasi OpenModelica 3. Langkah ketiga, dengan adanya variabel-variabel yang ada, kita dapat menemukan variabel yang dibutuhkan, dalam hal ini adalah variabel defleksi (U) serta variabel konstanta kekakuan(K) pada setiap elemen (sudah diketahui E=70 GPa, luas permukaan (A) = 1,5.10^-3m2 dan panjang batang untuk 3 variasi yaitu untuk 2.5m, 2.5m, dan 2.5m) 4. Langkah keempat, dengan didapatkannya variabel defleksi dan konstanta kekakuan batang, kita dapat menemukan persamaan gaya reaksi yang terjadi dengan rumus R=(K*U)-F 5. Langkah kelima, mensimulasikan dengan menggunakan aplikasi OpenModelica untuk mendapatkan hasil reaction force atau gaya reaksi pada setiap elemen.
Gambar-gambar di bawah ini adalah hasil simulasi dan screenshot bahasa modelica yang digunakan oleh Saudara Ahmad untuk menyelesaikan persoalan kuis nomor 8 ini:
Tugas 4: Mempelajari codingan Ahmad Mohammad Fahmi, dan mengaplikasikan pada contoh soal 3.3
1. Mempelajari Hasil OpenModelica yang dibuat oleh Ahmad Mohammad Fahmi
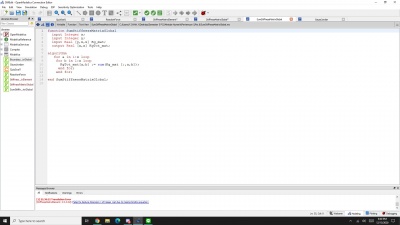
class QuizSoal1
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end QuizSoal1;
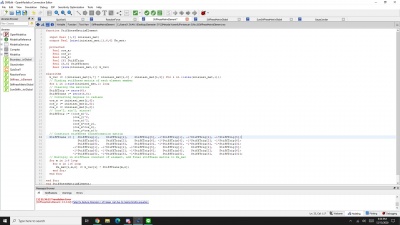
Dari codingan diatas, saya mempelajari hal baru yaitu untuk parameter "Real" berlaku untuk nilai angka bisa desimal, untuk parameter "Integer" berlaku untuk nilai angka bulat. Bahasa seperti "[:,9]" inisiasi menunjukkan matriks yang akan dipanggil dengan arti ":" berarti baris yang berarti dimensi sampai tak hingga, untuk "9" berarti kolom berjumlah 9. Untuk bahasa "inisiasi[i,7]" artinya bahasa ini digunakan untuk memanggil inisiasi dengan kode "i" yang berarti menuju ke matriks awal pada kolom ke 7 yaitu memanggil nilai A atau luas permukaan, untuk "inisiasi[i,8]" berarti untuk memanggil nilai pada matriks awal di kolom ke 8 atau E, dan "inisiasi[i,9]" untuk memanggil nilai pada matriks awal di kolom ke 9 atau L, hal itu digunakan untuk menghitung nilai k. Untuk kolom pada matriks yang awal dari kolom 1 sampai 9 menunjukkan variabel element, node, theta, A, E, L tetapi theta disini dijabarkan lagi menjadi dimensi x,y,z.
Kemudian, langkah selanjutnya adalah membuat atau mencari nilai Ke yaitu k pada setiap elemen, codingan yang digunakan terdapat bahasa baru yang saya pelajari yaitu,
StiffTrig := zeros(6); StiffTrans := zeros(6,6);
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
yang gunanya adalah memanggil inisiasi untuk kita kemudian bisa dapatkan hasilnya k pada setiap elemen untuk membentuk matriks elemen. Di akhir codingan kita menggunakan looping untuk mengulang perhitungan sebanyak 6 kali. Langkah selanjutnya adalah menyusun matriks global.
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Codingan yang digunakan seperti di atas yang menunjukkan rumus yang bisa dibuat untuk menyesuaikan matriks elemen untuk disambungkan menjadi matriks global. Langkah selanjutnya adalah menjumlahkan setiap Kg pada matriks global untuk kita dapatkan KgTot dan nanti di buat KgB yaitu boundary nya. Selanjutnya adalah mencari defleksi dengan codingan baru seperti berikut:
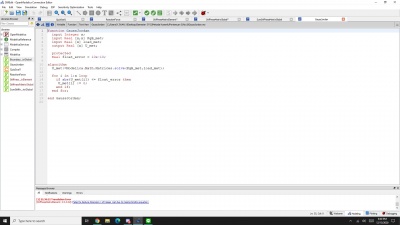
algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
Codingan di atas untuk menemukan U, dan saudara Ahmad menggunakan looping 1 sampai x, dan mengasumsikan jika U bernilai lebih kecil daripada float error yang telah ditentukan sebelumnya yaitu 10e-10 maka dianggap 0 dengan bahasa codingan yang digunakan "if abs(U_met[i]) <= float_error then U_met[i] := 0;". Langkah terakhir adalah menentukan reaction force dengan rumus codingan "R_met := (KgTot_met*U_met)-load_met;" yang artinya rumus R=(K*U)-F.
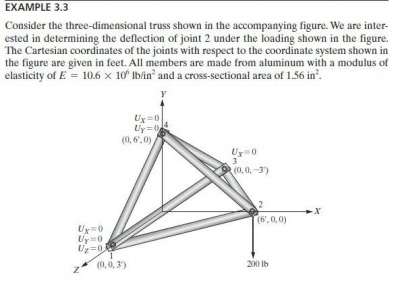
2. Mengaplikasikan bahasa OpenModelica yang digunakan Ahmad untuk menyelesaikan soal 3.3
Berikut adalah soal 3.3, menurut pandangan saya, tahap penyelesaian contoh 3.3 hampir sama seperti soal nomor 8 kuis minggu lalu, tetapi ada sedikit perubahan pada perhitungannya. Karena pada persoalan ini batang-batangnya tidak tumpuan fixed nya. Parameter-parameter yang diubah adalah seperti pada parameter sudut pada batang Ux,Uy,Uz disesuaikan soal; dimensi load menjadi berdimensi 3 Fx,Fy,Fz.
Berikut adalah hasil bahasa modelica yang saya gunakan untuk menyelesaikan masalah soal 3.3, dengan 1407 equation dan 1407 variables.
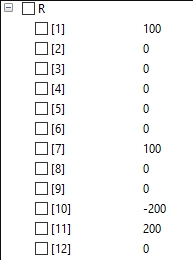
Berikut adalah hasil yang saya dapatkan untuk R, U dan F:
3. Masukkan atas codingan yang telah di buat Ahmad Mohammad Fahmi
Menurut saya, hasil codingan yang di buat oleh Ahmad Mohammad sudah baik, dimana ia membuat bahasa modelica untuk melakukan perhitungan secara manual secara keseluruhan pada aplikasi, mulai dari menentukan k, Ke, Kg, KgTot, KgB, U dan R. Saudara Ahmad juga pada codingan yang dibuatnya sudah menggunakan loop, sehingga data yang perhitungan yang banyak dapat dilakukan secara otomatis oleh software dengan mudah dan meminimalisir error yang terjadi pada perhitungan.
Pada codingan saudara Ahmad juga menggunakan new modelica class yaitu tipe class dan function, tidak disatukan pada class tipe model, dimana keuntungan dari dipisahnya kelas-kelas adalah memudahkan penulis untuk mengedit-edit bahasa codingan yang menurut dia salah atau akan di ganti nantinya. Keuntungan lain adalah pada pembaca, karena di sini saya sebagai pembaca merasa dimudahkan karena kelas-kelasnya telah dipisah sehingga cukup jelas untuk setiap bahasa digunakan untuk ap dan terlihat lebih rapi. Dengan dipisahnya class dan function juga memberikan kemudahan bagi kita untuk mengerjakan permasalahan yang ada untuk kedepannya, karena sudah rapi tersusun, tinggal memikirkan tentang perbedaan angka pada soal dan mungkin boundary condition yang terdapat pada setiap node dan perbedaan struktur apakah soal yang ada berdimensi 2 atau 3.
Selanjutnya untuk hasil coding dari no 3.3 yang dikerjakan juga menerapkan sistem yang sama, dimana soal yang dibahas mengenai struktur berdimensi 3, tetapi disini terdapat beberapa perubahan untuk menyelesaikan permasalahan 3.3 seperti bentuk node-node, boundary yang digunakan mengingat node-node pada batangnya tidak memiliki tumpuan, parameter real dan lain-lain. Namun, secara garis besar menurut saya codingan saudara Ahmad ini cukup membantu saya menyelesaikan persoalan 3.3 karena sudah mewakili sebagian besar bahasa modelica nya untuk kemudian digunakan untuk menyelesaikan permasalahan dengan output baik itu defleksi dan reaction force.
Pertemuan 6: 14 Desember 2020
Pada pertemuan kali ini, Pak Dai memberikan wadah untuk berdiskusi mahasiswa akan muhasabah diri mengenai materi pembelajaran mata kuliah metode numerik. Mahasiswa diharapkan mampu menilai diri sendiri atas pemahaman yang dipahami setiap mahasiswa, dan mencoba menjelaskan apa saja yang sudah dipelajari selama perkuliahan jarak jauh ini.
Kemudian, pembelajaran dilanjutkan dengan pemaparan materi oleh saudara Christo dari kelas Metode Numerik 02 mengenai pemahaman dari alur berfikir mengenai soal-soal yang telah diberikan, kemudian diterapkan pada software Openmodelica, tentang cara mengenai bagaimana menerjemahkan permasalahan soal ke penerapan aplikasi Openmodelica. Hal-hal yang perlu digarisbawahi adalah cara mengidentifikasi parameter apa saja dari soal yang diketahui, cara membentuk model dan cara melakukan perhitungan dari model soal seperti melibatkan function apa saja yang digunakan. Selain itu, pemaparan materi juga disampaikan oleh saudara Josiah Enrico dan saudara Ahmad Mohammad Fahmi sebagai perbandingan dari alur pengerjaan soal-soal yang telah diberikan dan perbedaannya.
Pertemuan 7: 21 Desember 2020
Pada pertemuan kali ini, di mulai oleh Pak Dai dengan penyampaian penyelesaian tugas besar.
Truss berbeda dengan beam, Pada truss setiap titik hanya punya 3 derajat kebebasan dengan variabelnya displacement dalam x,y,z untuk asumsi batang. Mahasiswa diharapkan betul betul terlihat kenapa kita harus belajar metnum dan aplikasi di dalam bidang kita jika kita mengerjakan tugas besar.
Sedangkan pada beam berbeda, pada rangka ada 6 derajat kebebasan dengan variabel displacement x,y,z da ke arah momen atau puntirannya. Dari asumsi tadi mahasiswa diharap menyusun persamaan-persamaannya. Selanjutnya langkahnya dari profil truss siku yang diberikan pada WA Group. Dengna menyusun persamaan-persamaan tadi mahasiswa diharapkan mengerti dan memahami cara menyelesaikan permasalahan tadi dengan matriks dan variabel-variabel lain untuk diaplikasikan pada aplikasi OpenModelica. Kita harus mengerti menyusun persamaannya dan boundary condition dan seterusnya.
Kami mahasiswa diharapkan menghitung kondisi optimal pada rangka dengan parameter seperti tujuan dan fungsi objektif pada optimasi, harus ada fungsi-fungsi pada batasan atau constraints nya (berapa panjang siku, berapa harganya per beberapa ukuran). Tujuan dari optimisasi adalah meminimalisir biaya. Constraintnya harus mampu menahan beban artinya gaya-gaya bekerja itu yang berupa tegangan harus mampu didukung pada rangka ini. Awalnya kita diharuskan mencari displacement, mengcrosscheck gaya nya, dan mengoptimasi gaya tersebut dan menghitung gaya atau stress tadi dan kita selanjutnya membandingkan stress dari kekuatan materialnya itu sendiri. Perhitungan tegangan yang terjadi tidak boleh melebihi dari allowable stressnya agar membentuk rangka yang sesuai standar. Dari data tadi, kita akan mendapatkan jenis material dan ukuran dari batang dan kita bisa tahu berapa spesifikasi siku. Kemudian per batang ada harganya. Dari data-data tadi kita lakukan optimasi untuk mengetahui yang mana bahan yang paling optimal. k= A.E/L, jadi A luas penampang siku nya, E modulus elastisitas tiap bahan, L panjang batang rangka. Yang perlu digarisbawahi adalah batang yang dipilih adalah profil siku seperti galvanis, stainless dan lain lain.
Kurva karakteristik pompa, sumbu bawah adalah debit, sumbu y adalah head. Si pompa ini mempunyai karakteristik effisiensi. Seperti gambar di bawah ini:
Kemudian, dilanjutkan dengan Bu Candra, dengan menyampaikan powerpoint dimana optimasi yang digunakan adalah metode bracket optimization using golden ratio. PPT ini dapat di akses di WA Group. Lalu kita mahasiswa diharapkan mengikuti simulasi dengan menggunakan aplikasi OpenModelica untuk menyelesaikan permasalahan dengan fungsi exercise yang telah diberikan dan tercantum dalam PPT. Berikut adalah penyelesaiannya.
Kesimpulannya adalah dari awal penyampaian tugas besar nya, secara garis besar persamaan truss. Kalo fungsi optimasi, kita harus memiliki fungsi objektif seperti kita mendapatkan stress yang maksimum dan biaya yang minimum. Lalu variabel yang dapat di ubah adalah dimensi dari truss siku tadi dan juga dari raw material nya. Cara menyelesaikan tugas besar awalnya, di buat alur proses atau flowchart cara penyelesaian optimasi tersebut, kemudian kita cari 3 material yang berbeda untuk kita coba mensimulasikannya dengan tugas besar masing-masing. Kemudian tentukan Fungsi objektif, tentukan fungsi constraints nya yaitu stress tidak kurang dari setengah allowable stressnya. Kemudian membandingkan dengan yang ada di tabel di buku.
Tugas Besar Metode Numerik
Data-data yang diketahui:
Berikut adalah geometri yang diberikan oleh Pak Dai:
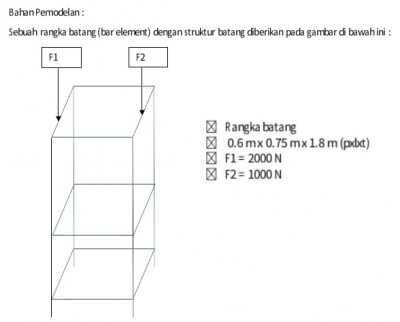
Diketahui: spesifikasi dan geometri truss F1=2000 N F2=1000 N
Asumsi: safety factor= 2 batas displacement= 0,001m (sebelum buckling) variasi stiffness beban terdistribusi pada node (karena trusses)
Data-data yang digunakan:
1) Elastisitas sama
2) Area sama
Codingan yang digunakan:
Displacement limit= 0,0005 m
A yang digunakan= 0.00001957397
Stiffness Constant (A*E) = 3719054.3
Total Length=15,3 m
Untuk membuat trusses 3d:
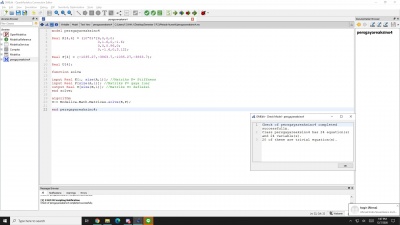
model tugasbesarmetnummizan
//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=3719054.3; //Area
parameter Real Elas=1; //Elasticity (equals to one in order to determine the displacement limit)
//define connection
parameter Integer C[Trusses,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[Points,3]=[0.3,-0.375,0; //1
-0.3,-0.375,0; //2
-0.3,0.375,0; //3
0.3,0.375,0; //4
0.3,-0.375,0.6; //5
-0.3,-0.375,0.6; //6
-0.3,0.375,0.6; //7
0.3,0.375,0.6; //8
0.3,-0.375,1.2; //9
-0.3,-0.375,1.2; //10
-0.3,0.375,1.2; //11
0.3,0.375,1.2; //12
0.3,-0.375,1.8; //13
-0.3,-0.375,1.8; //14
-0.3,0.375,1.8; //15
0.3,0.375,1.8]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define boundary
parameter Integer b[:]={1,2,3,4};
//solution
Real displacement[N], reaction[N];
Real check[3];
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10;
Real ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
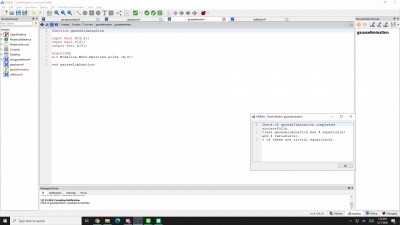
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
end tugasbesarmetnummizan
Untuk membuat curve fitting:
Curve Fitting Function
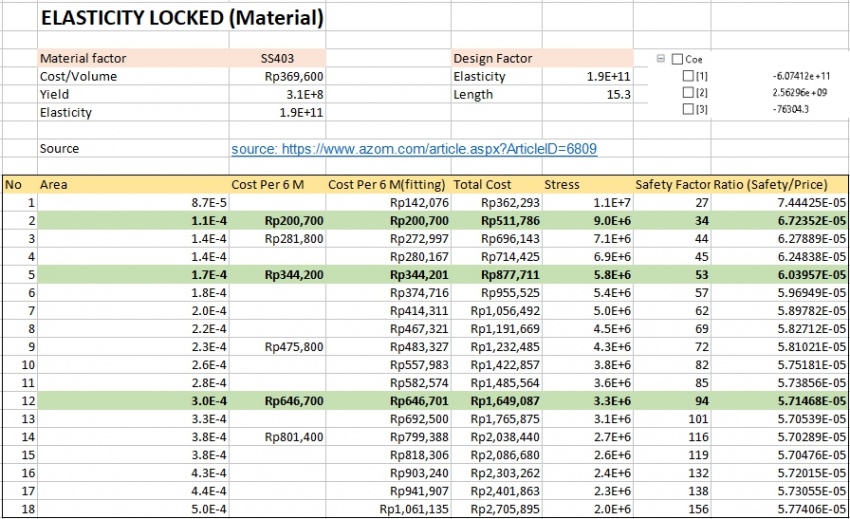
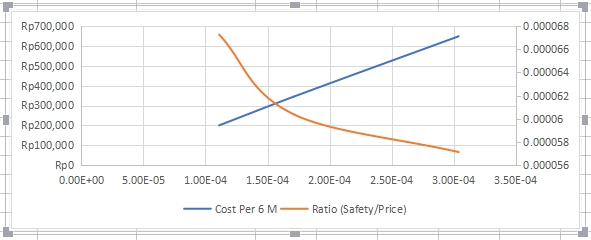
1. Curve fitting untuk elasticity lock
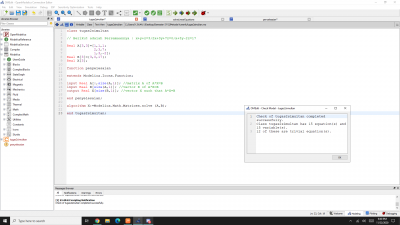
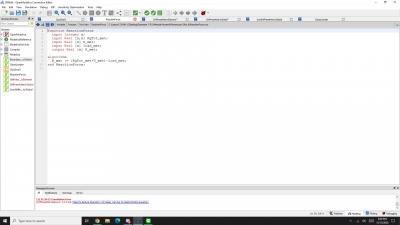
class curvefitting
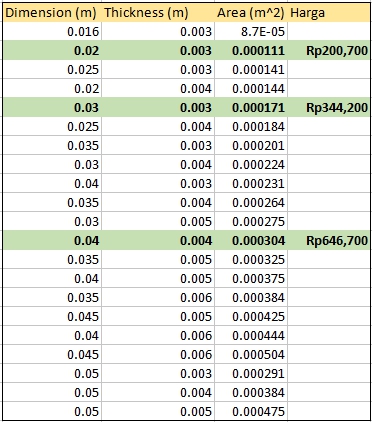
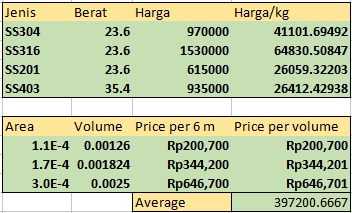
parameter Real X[3]={111E-6, 171E-6, 304E-6}; //Area/ Elastisitas
parameter Real Y[3]={200700, 344200, 646700}; //Area/ Cost/ Density/ Yield
Real Coe[3];
algorithm Coe:=opt(X,Y,2);
end curvefitting;
dan memanggil fungsi curve fitting di bawah ini:
function opt input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end opt;
Hasil Perhitungan:
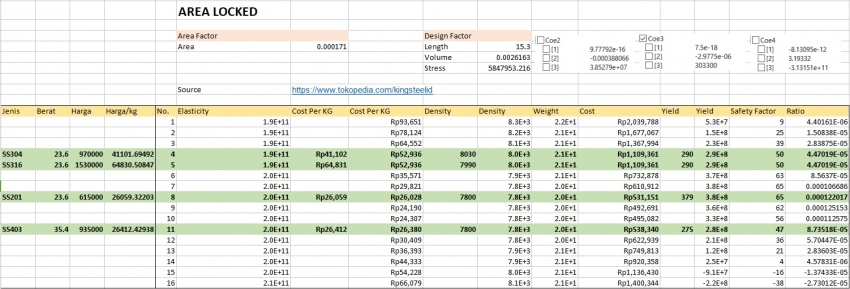
1) Elastisitas sama
2) Area sama
UAS Metoda Numerik 03
Jawaban UAS
Berikut adalah hasil kerja UAS Metode Numerik saya yang dilaksanakan pada hari ini Rabu, 13 Januari 2021, pukul 16.00-18.00
Penjelasan No.1 :
Permasalahan water tower tadi dapat diselesaikan dengan beberapa langkah
1. Masalah Teknik - masalah teknik yang dijadikan acuan adalah struktur finite element pada batang dengan persamaan, mencari node dan elemen pada masing-masing titik 2. Analisis Masalah - dari analisis masalah kita dapatkan pertanyaan atau studi kasus 3. Model Matematis - dilakukan model matematis dengan hukum fisika 4. Model Numerik - dari hukum fisika kita dapat turunkan menjadi model numeriknya 5. Komputer - ditranslasikan dengan software komputer dalam hal ini adalah OpenModelica 6. Solusi - ketemu solusi displacement ataupun gaya reaksi dan stress pada batang water tower (U,F)
Penjelasan No.2 :
- Tujuan dan Asumsi --> Tujuan pemodelan numerik, untuk menghitung kekuatan struktur. Dilakukan perhitungan permodelan water tower ini untuk perbandingan ataupun optimasi dari sistem yang sudah ada dengan berbagai asumsi dan variabel yang setiap mahasiswa tentukan sendiri-sendiri; Asumsinya adalah gaya luar yang diberikan, material struktur truss 1D water tower agar optimal. Asumsi lain adalah node terdistribusi, safety factor dan batas displacement dari gaya luar pada batang.
- Hukum fisika --> Hukum yang digunakan hukum fisika pada pemodelan tersebut, pada umumnya melibatkan utamanya hukum hooke, hukum newton karena hukum tersebut berkaitan langsung dengan gaya luar, konstanta kekakuan, dan juga displacement. Dimana ketiga variabel tersebut digunakan dan menjadi hasil akhir dalam perhitungan optimasi truss 1D water tower yang dipakai. Beberapa rumusan lain seperti yield strength, modulus elastisitas, Area, tinggi tower yang juga digunakan sebagai parameter perhitungan pada optimasi.
Penjelasan No.3 :
Pada nomor 3 dibuat variabel atau persamaan untuk membentuk matriks global, dimana untuk matriks lokal, matriks yang digunakan berdasarkan turunan dari U1x, U1y, U2x, U2y karena pada pemodelan truss 1D menggunakan dua axis yaitu x dan y. Matriks lokal yang telah didapatkan untuk dx dan dy dicari sudutnya untuk diinput ke matriks lokal. Dari matriks lokal tadi, dijumlahkan semua hasil dari masing-masing hasil matriks lokal untuk membentuk matriks global.
Penjelasan No.4 :
Dibuat flowchart untuk pseudocode dari optimasi permodelan. Dengan tahapan awal memasukan atau input data-data yang diketahui, kemudian membuat matriks kekakuan elemen lokal dan mentransformasikan elemen global, menentukan boundary, lalu dapat ditemukan output displacement, reaction force dan check force untuk memastikan gaya yang terjadi.
Penjelasan No.5 :
Pada no. 5, mengenai fungsi objective dan constrain yang digunakan pada node-node dari struktur.
Penjelasan No.6 :
Pada no. 6 berisi asumsi yang akan digunakan dalam menghitung pemodelan di openmodelica disini saya menggunakan: Area = 0.0005(m2); Yield strength= 310e6 //(SS403)(Pa); Elas=1.9e11 //(SS403)(Pa). Serta asumsi gaya pada node 4 = 100N dan L= 12 feet dengan l1,l2,l3=4 feet
Penjelasan No.7 :
Berikut adalah codingan yang mendukung jawaban nomor 7 yang saya gunakan untuk menyelesaikan permasalahan truss 1D sesuai dengan asumsi pada nomor 6:
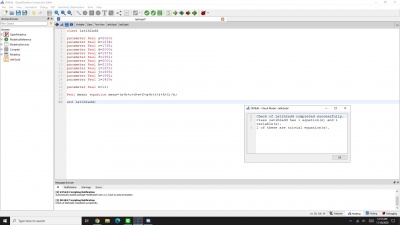
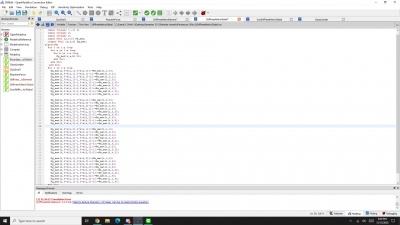
model UASMetnumMizan
/*Nama = Mizan Eryandhika Guntorozi
NPM = 1806181823 */
parameter Real P[3]={30000,0,30000};//beban dan gaya reaksinya (beban berada pada node 3 yang negatif dan gaya reaksi pada node 1 dengan nilai positif)
//asumsi semua elemen sejenis
parameter Real a=5e-4;//luas penampang (m2)
parameter Real e=1.9e11;//elastisitas (SS403)(Pa)
parameter Real l=13.33;//tinggi L=40m dan dibagi 3 menjadi l=13.33m (m)
//parameter yang akan dicari Real k;//kekakuan elemen Real kg[3,3];//matriks global Real u[3];//displacement Real stress[3];//stress yang dialami algorithm //mencari nilai kekakuan k := a*e/1;
//menuliskan persamaan matriks global
kg := [k, 2*k, 0;
-k, 2*k, -k;
0, -k, 2*k];
//mencari displacement dengan metode gauss-jordan u := Modelica.Math.Matrices.solve(kg,P);
//mencari stress pada tiap elemen stress[1] := u[1]*k/a; stress[2] := u[2]*k/a; stress[3] := u[3]*k/a;
end UASMetnumMizan;
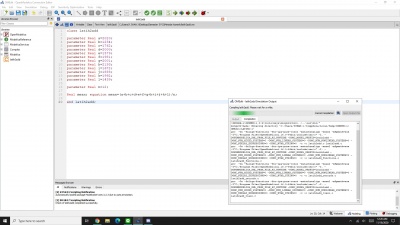
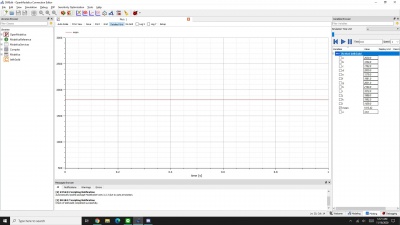
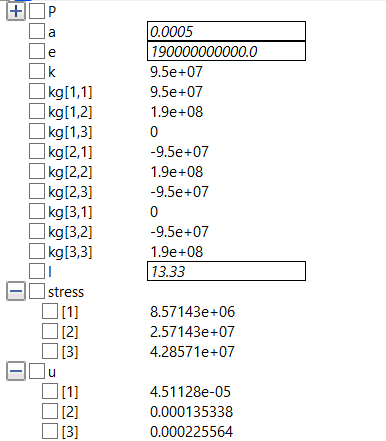
Berikut adalah hasil simulasi codingan di atas dengan material SS403 dimana, A=Area= 0.0005m2; Yield= 310e6; E= 1.9e11; l1,l2,l3= 13.33m;
Terdapat perbedaan ketika melakukan simulasi, karena ada beberapa variabel seperti A, E dan L serta node-node yang diasumsikan belum sesuai dan saya salah menginput nilai pada aplikasi OpenModelica.