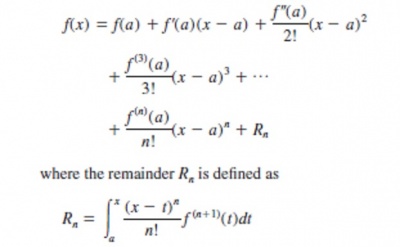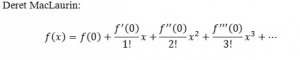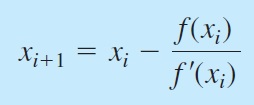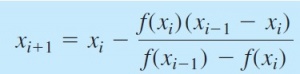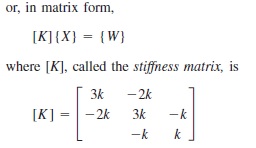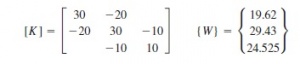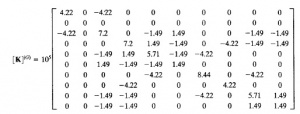Metnum03-Christian Emanuel Kefi
Contents
- 1 BIODATA DIRI
- 2 Pertemuan Metode Numerik-03
- 3 Pertemuan Sebelum UTS
- 4 Pertemuan 1 : Senin,9 November 2020
- 5 Tugas 1 : Muller's method menggunakan Openmodelica
- 6 Pertemuan 2 : Senin,16 November 2020
- 7 Tugas 2 : Class type function - untuk menyelesaikan persamaan aljabar simultan
- 8 Pertemuan 3 : Senin,23 November 2020
- 9 Tugas 3 : Beam
- 10 Pertemuan 4 : Senin,30 November 2020
- 11 QUIZ Metnum 1
- 12 Pertemuan 5 : Senin, 7 Desember 2020
- 13 Tugas 5 : Quis 1, Example 3.3
- 14 Pertemuan 6, Senin 14 Desember 2020
- 15 Pertemuan 7, Senin 21 Desember 2020
- 16 TUGAS BESAR, Optimasi truss
- 17 Jawaban UAS
BIODATA DIRI
Nama : Christian Emanuel Kefi
NPM : 1906435460
Pendidikan Terakhir : Diploma III
Pertemuan Metode Numerik-03
Pertemuan Sebelum UTS
Pada pertemuan sebelum UTS ada 4 materi utama yang dipelajari, antara lain :
1. Kesalahan Pembulatan, Deret Taylor dan Derer Mclaurin
Kesalahan pebulatan atau truncation errors, misalnya dalam duatu penyelesaian fungsi biasanya diambil pendekatan dengan angka penting terkecil, sehingga terjadi perbedaan antara nilai pembulatan dengan nilai sebenarnya. Nilai sebenarnya tidak terhingga, sehingga digunakan deret Taylor untuk menyelesaikan suatu fungsi tersebut. Deret Taylor menentukan pendekatan suatu fungsi secara polynomial sehingga deretnya tidak terbatas.
Berikut adalah formula dari deret Taylor :
Dimana Rn adalah sisa.
Sementara deret Mac Laurin merupakan khasus khusus dari deret Taylor dimana menggunakan fungsi ekspansi c=0
Salah satu contohya mencari deret Mac Lurin untuk sin (x) :
2. Roots of Equation
Dalam pelajaran ini mencari akar-akar dari suatu polynomial dengan metode-metode sebagai berikut : Bracketing Method (Closed Method) dan Open Method
Bracketing method :
Metode mencari akar-akar dari suatu polynomial dengan menetapakn batasan dan mencari nilai erornya. Metode-metode pada closed method ini antara lain :
- Graphical method : menggunakan grafik untuk mencari akar-akar. Dilakukan dengan cara meng-ploting / memasukan angka pada suatu polynomial sehingga terbentuk grafik.
- Bisection Method : merupakan metode dimana menggunakan batasan atas bawah dan dilakukan secara incremental untuk mempersempit error.
- False – position Method : metode ini mirip dengan Bisection method, yang membedakan adalah cara menentukan titik tengahnya.
Open Method :
Merupakan metode dimana hanya menggunakan 1 titik pendekatan untuk menentukan akar-akar sebenarnya :
- Newton Raphson Method : Metode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut:
- Secant Method : Metode ini digunakan jika f”(Xi) sulit didapatkan sehingga digunakan rumus sebagai berikut :
3. Regresi Linier dan Interpolasi
Regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.
4. Turunan Numerik
Diajarkan cara untuk menentukan nilai pendekatan turunan suatu fungsi yang diberikan dalam bentuk tabel. Pendekatan dilakukan dengan 3 cara (forward, backward & centre)
Pertemuan 1 : Senin,9 November 2020
Pada pertemuan kali ini mereview pembelajaran sebelum UTS dan meberikan 4 indikator dalam pembelajaran yang pertama mengetahui apa yang dipelajari, yang kedua paham konsep pembelajaran yang sudah dipelajari atau diketahui tersebut, ketiga pengaplikasian dari suatu materi/konsep yang sudah dipelajari, keempat mengenali diri/ menilai diri sendiri dalam pengaplikasian yang sudah dipelajari.
Selain itu pertemuan ini disertai pemberian tugas untuk mencoba membuat program pada aplikasi openmodelica. link dibawah menghubungkan dengan video tugas tersebut.
Tugas 1 : Muller's method menggunakan Openmodelica
https://www.youtube.com/watch?v=tKEca_-MpMI
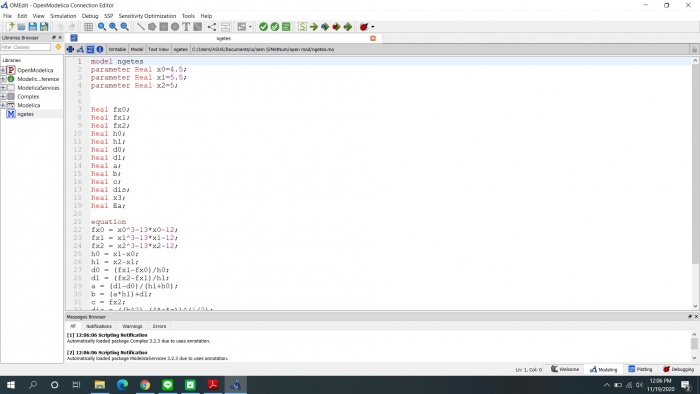
Dalam metode ini menggunakan 3 titik tebakan yang nantinya akan dimasukan kedalam persamaan kuadrat untuk mendapatkan hasil yaitu sebuah titik potong dari sebuah garis polinomial dan garis sumbu-x. Titik tersebut merupakan pendekatan untuk menemukan akar-akar dari suatu polinomial. semakin banyak iterasi yang dilakukan semakin dekat hasil perhitungan yang dilakukan dengan akar yang sebenarnya. Gambar berikut menunjukan contoh dari program perhitungan yang menjawab suatu persoalan menemukan akar-akar dari suatu polinommial :
Parameter digambar itu merupakan nilai yang diketahui atau yang nantinya akan diinput, dan nilai real adalah nilai yang ada dalam perhitungan baik yang diketahui maupun yang akan dicari.
Pertemuan 2 : Senin,16 November 2020
Pada pertemuan kali ini dilakukan penilaian terhadap PR pertama, yaitu mempelajari aplikasi openmodelica. Dari tugas tersebut saya membahas tentang Muller methods seperti yang tertera diatas.
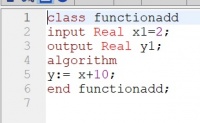
1) Dalam pertemuan ini juga diberikan tugas membuat permodelan sederhana yaitu menjumlahkan angka 10 terhadap suatu variabel.
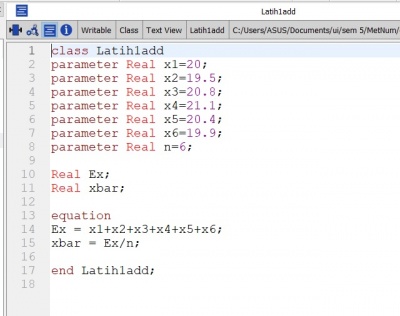
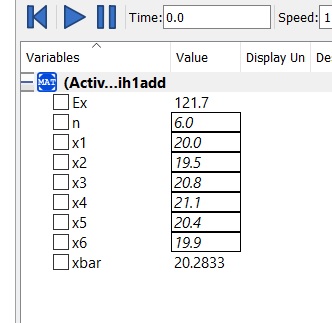
2) Selain itu juga membuat persamaan untuk mencari nilai rata-rata dari suatu data tertentu.
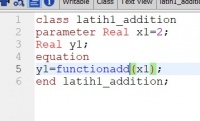
3) Selanjutnya dilakukan percobaan menbuat function class dari class pada no.1. contohnya sebagai berikut :
Tugas 2 : Class type function - untuk menyelesaikan persamaan aljabar simultan
Persamaan aljabar simultan adalah persamaan aljabar yang mempunyai lebih dari satu persamaan dan diselesaikan secara simultan. Pada umumnya, jenis persamaan aljabar simultan dapat diselesaikan dengan metode grafik, metode subtitusi, metode eliminasi gauss, dan metode cramer.
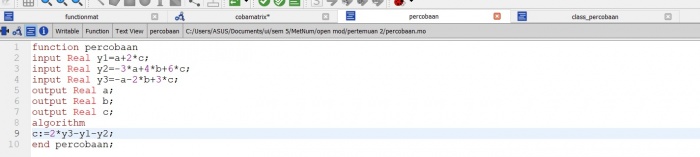
Pada percobaan pertama menggunakan metode class function pada open modelica dengan contoh soal sebagai berikut :
x1 + 2.x3 = 6
-3.x1 + 4.x2 + 6.x3 = 30
-x1 - 2.x2 + 3.x3 = 8
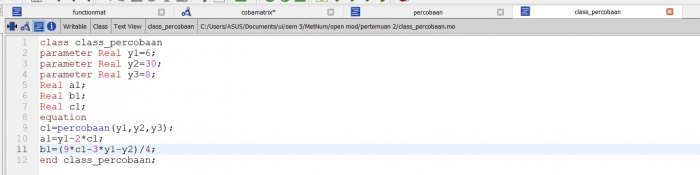
dengan contoh program function dan class sebagai berikut :
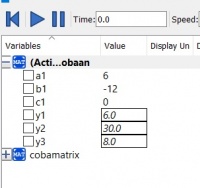
Dan hasil percobaan sebagai berikut
Pertemuan 3 : Senin,23 November 2020
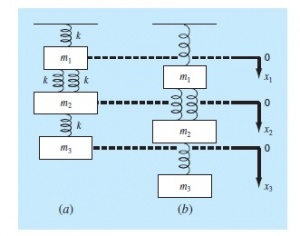
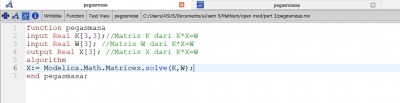
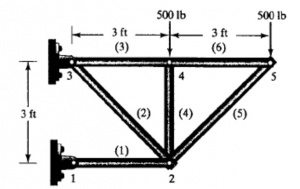
Pada pertemuan ketiga ini dijelaskan tentang masalah teknik berupa sistem pegas-masa yang terdapat pada contoh 12.11 pada buku metode numerik.
spring mass system dapat diselesaikan dengan menggunakan persamaan dari hukum Hooke. dimana variable yang digunakan sebagai berikut :
m = massa benda (kg)
k = konstanta pegas
x = Jarak perpindahan (m)
Fd-Fu = force up dan force down = merupakan force balance (zigma F)
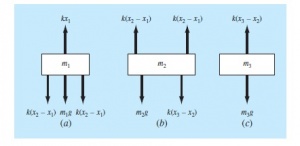
Dari gambar diatas dapat disimpulkan gaya yang bekerja pada setiap komponen diatas adalah :
1) Benda 1
kx1 = 2k(x2-x1) + m1g ----> 3kx1-2kx2=m1g
2) Benda 2
2k(x2-x1)=m2g+k(x3-x2)) -----> -2kx1 + 3kx2 - kx3 = m2g
3) Benda 3
k(x3-x2) = m3g
Untuk mencari nilai dari x digunakan persamaan sebagai berikut:
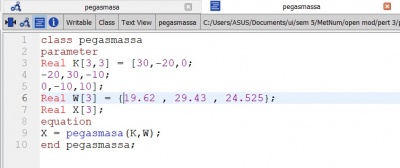
Dengan persamaan tersebut dimasukan nilai k=10 kg/s^2, dan m1 = 2 kg, m2 = 3 kg, dan m3 = 2,5 kg didapatkan hasil sebagai berikut :
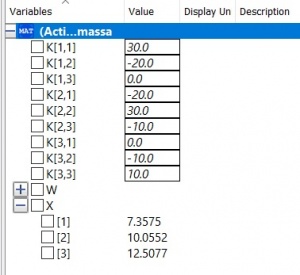
Dengan menggunakan aplikasi open modelica didapatkan nilai dari x1, x2, x3 dengan langkah-langkah sebagai berikut :
Tugas 3 : Beam
Pada tugas kali ini mencari gaya reaksi dan defleksi pada setiap titik dari beam dibawah gaya tekan seperti dibawah ini :
Semua kerangka beam terbuat dari kayu yang memiliki modulus elastisitas E = 1,9 x 10^6 lb/in dan A = 8 in^2
untuk mencari defleksi dan gaya reaksi hal yang dilakukan adalah :
1) Melakukan analisis node i, j, dan sudut dari setiap element
2) Mencari nilai kekakuan dari setiap element
- Elemen 1,3,4,6 memiliki kekakuan yang sama karena memiliki A, E, dan L yang sama
- Elemen 2, dan 5 memiliki kekakuan yang sama
3) membuat persamaan elemen-elemen
4) Dari no 3 didapatkan matriks dari individual elemen matrix, pada tahap ini dilakukan penggabungan terhadap semua individual elemen matrix
dan disederhanakan menjadi sebagai berikut :
5) Dari data yang didapatkan dari buku didapatkan matriks 10 x 10 :
karena nilai dari U1x, U1y, U3x, dan U3y = 0 , maka matriks dapat disederhanakan menjadi bentuk 6 x 6
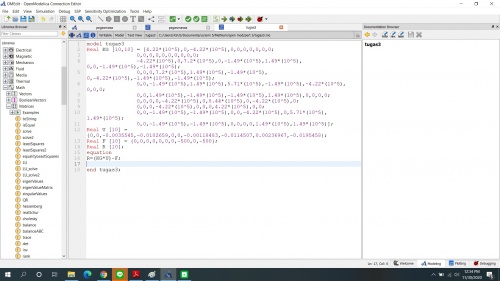
Apabila dikerjakan dengan matrix pada open modelica hasilnya sebagai berikut :
Pertemuan 4 : Senin,30 November 2020
Pertemuan ini diisi oleh pak Ahmad Indra diawali dengan menjelaskan tentang struktur statik dan struktur dinamik, dimana struktur static merupakan sistem yang bersifat tetap atau tidak berubah bedasarkan waktu sementara sistem dinamik adalah struktur yang memiliki fungsi waktu. dalam pertemuan ini juga diberikan kuis 2 nomor struktur 2 dimansi dan 3 dimensi.
QUIZ Metnum 1
Langkah-langkah dan hasil quis no.4
Berikut adalah coding untuk no 4
| Soal no.4 |
|
Langkah-langkah dan hasil quis no.8
hasil No 8 menggunakan excel :
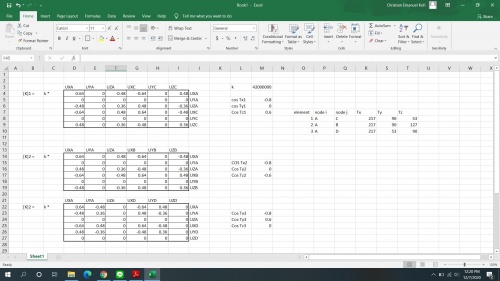
Untuk permodelan 3D digunakan stiffness matrix dari space trusses dengan hasil sebagai berikut :
Pembuatan matrix lokal dan global dilakukan menggunakan excel karena lebih mudah dalam penulisan, perhitungan dan penempatan.
Setelah didapatkan matriks lokal digabungkan menjadi matriks global dengan meng-copy paste sesuai tempat pada matrix global
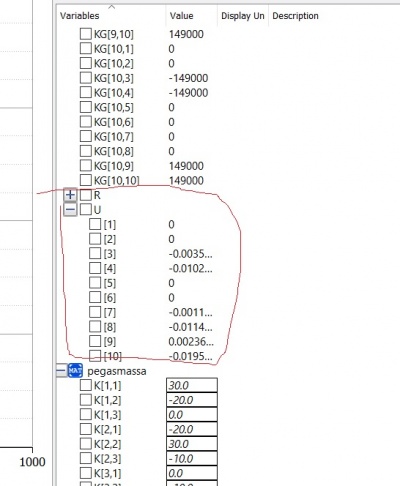
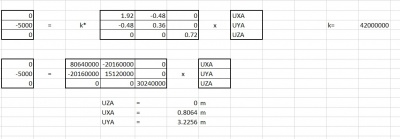
dengan memasukan kondisi batas dimana terjadi gaya tarik ke bawah searah sumbu Y sebesar 5000 N pada titik D, maka nilai-nilai dibawah ini sama dengan 0:
U2x = U2y = U2z = U3x = U3y = U3z = U4x = U4y = U4z = 0
F1x = F1z = F2x = F2y = F2z = F3x = F3y = F3z = F4x = F4y = F4z = 0
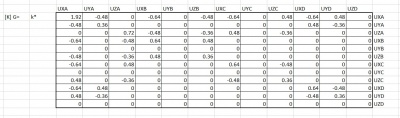
Dari kondisi tersebut matriks dapat disederhanakan menjadi 3x3 seperti dibawah ini :
Berikut adalah coding untuk no 8
| Soal No.8 |
|
Pertemuan 5 : Senin, 7 Desember 2020
Pertemuan kali ini membahas tentang kuis yang diberikan pertemuan sebelumnya, dalam kasus ini kebanyakan mahasiswa blum memahami tentang cara menggunakan looping pada openmodelica. pertemuan kali ini dibantu oleh ahmad fahmi dalam penjelasan metode looping untuk pengerjaan kuis 1. Dari hasil dan penjelasan yang didapat mahasiswa diharapkan untuk mencoba kembali dengan kasus example 3.3 yang diberikan sebagai tugas berikutnya.
Tugas 5 : Quis 1, Example 3.3
1. Mempelajari codingan 3d Fahmi
2. Mengaplikasikan pada soal example 3.3
3. memberikan masukan atas codingan Fahmi
Serta uraikan pembahasannya di wikipage masing-masing termasuk pembahasan FlowChart, Diagram Class dan Coding tambahan anda sebagai kontribusi coding lebih aplikatif, efffisien dan robust.
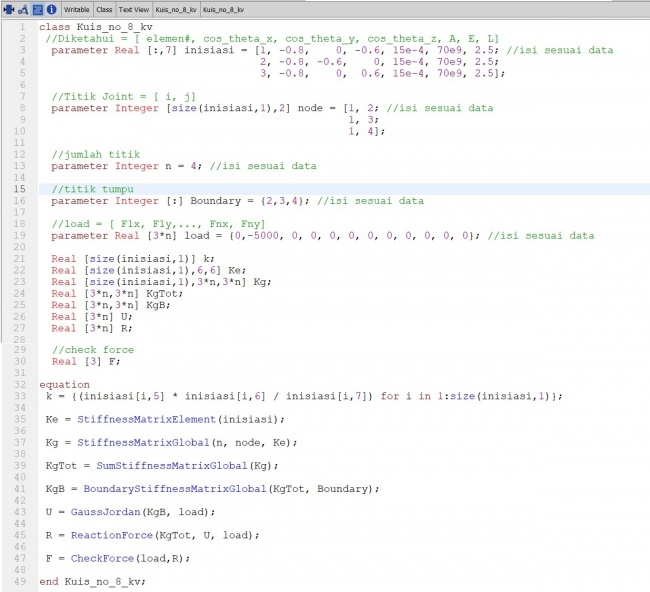
1. Setelah mempelajari hasil coding dari Ahmad Fahmi, saya mememahami cara penggunaan loop dalam open modelica selain itu ilmu baru yang saya dapatkan adalah mempelajari Bahasa-bahasa baru dalam pemrograman open modelica seperti contoh dibawah ini :
- Dalam text view terlihat tulisan berwarna hijau, itu merupakan penanda atau note yang berfungsi memberikan keterangan dan tidak ter input kedalam hasil maupun masukan.
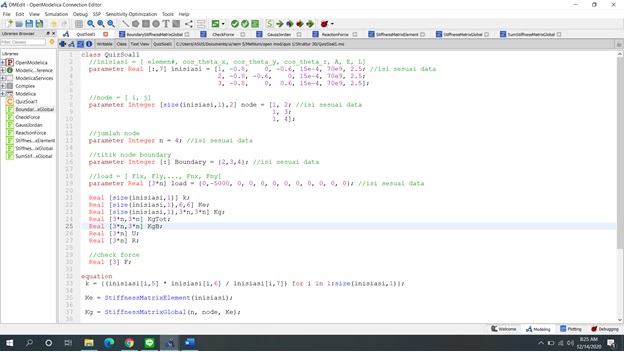
- Terlihat juga inisiasi, sebenarnya itu hanya merupakan penamaan, dan sebenarnya bebas tergantung masing-masing memberikan nama.
- Integer & real = integer merupakan merupakan bilangan bulat sementara real bisa bilangan bulat maupun decimal.
- Selain itu ada tanda titik dua ( : ) itu merupakan tanda dari infinity
- Pada baris no 10 terdapat tulisan “[size(inisiasi,1),2]” , itu berarti pada baris memanggil matriks inisiasi 1 = baris ; 2 = kolom, sehingga dalam codingan tersebut no 1 berarti infinity pada matriks inisiasi.
- “n” yang dimaksud dalam class ini adalah jumlah node/sambungan/titik
- Boundary yang dimaksud adalah titik tumpu/fix yang tidak menyebabkan defleksi, dalam soal terletak pada titik 2,3 dan 4
- Dalam parameter load terlihat bahwa beban = 3*n karena meninjau n titik dalam 3 dimensi.
- [size(inisiasi,1)] = jumlah yang dihasilkan sesuai jumlah baris pada inisiasi dan tidak dalam bentuk matrix
- [size(inisiasi,1),6,6] Ke = jumlah Ke yang dihasilkan sesuai jumlah baris pada inisiasi dan dalam bentuk matrix 6 x 6 sesuai dengan rumus 3D.
- Pada equation “k” terdapat (inisiasi[i,5]) yang berarti I adalah variable yang akan di looping pada bagian baris dan 5 berarti menunjukan kolom ke 5.
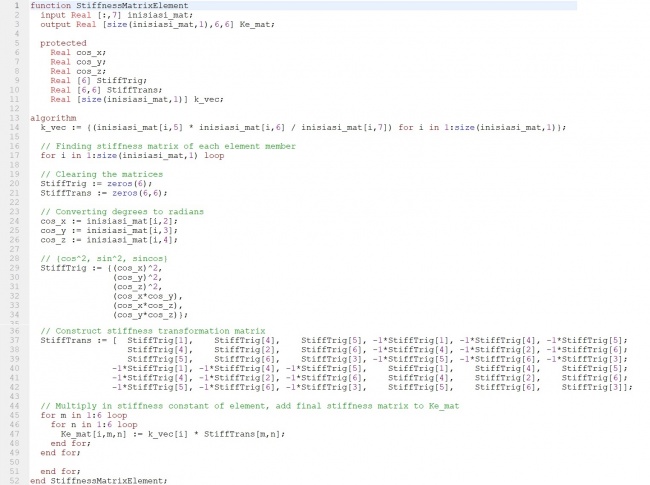
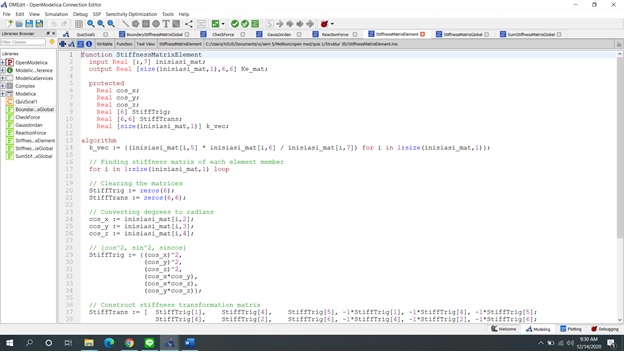
- Dalam StiffnessMatrixElement input inisiasi_mat itu sama saja dengan inisiasi tetapi tempatnya di function, namanya berbeda namun terhubung / sama karena [:,7]. Input tersebut berdasarkan variable dalam kurung pada equation “Ke” diatas.
- StiffTrig = rumus dalam matrix Ke hanya ada 6 jenis
- Stifftrans = matrix pola K elemen
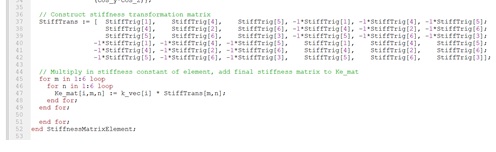
- Zeros = meng nol kan matrix
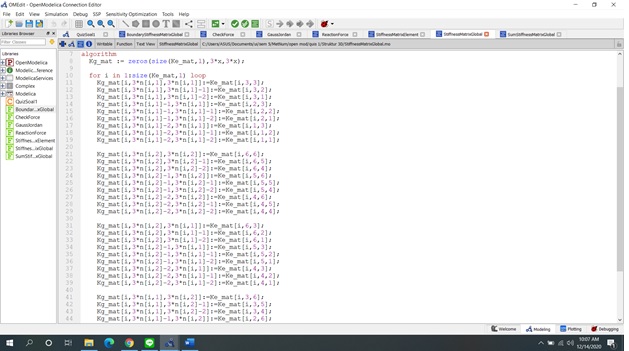
Dalam function StiffnessMatrixGlobal ini walaupun menggunakan looping tetapi masih harus menginput satu per satu posisi pemindahan dari matriks K element ke matriks K global.
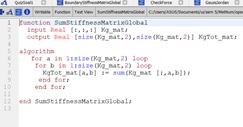
Untuk SumStifnessMatrix ini hanya penjumlahan semua matrix global dari setiap elemen. Jadi inputnya [: , : , :] merupakan [jumlah, baris, kolom] dan output memiliki jumlah hanya 1 jadi hanya menjadi [baris , kolom]. Cara menghitungnya seperti di algoritma, menggunakan perintah sum, dan pada setiap baris dan kolomnya di looping.
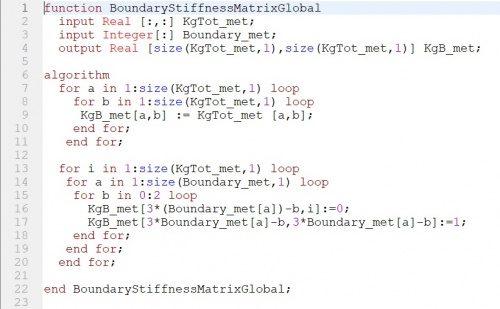
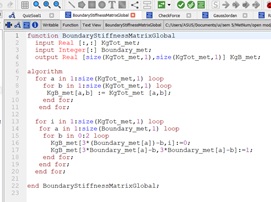
Untuk K global yang, merupakan K global yang sudah mengikuti boundary, atau dalam hiungan manual pada titik tumpu nilai defleksi = 0. Input dari function ini berasal dari KgTot dan boundary dengan output berukuran sama dengan K global.
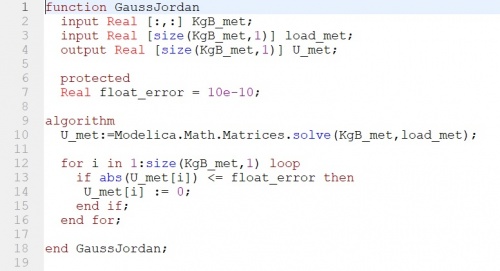
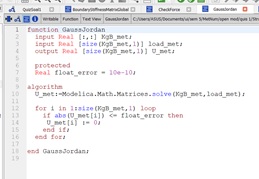
Gaus Jordan dipakai untuk mencari nilai U, dan menggunakan perhitungan dari matrix yang terdapat pada modelica. Dalam perhitungan juga diselipkan floating eror agar nilai yang terhitung terlalu kecil atau dibawah batas floating eror akan menjadi 0.
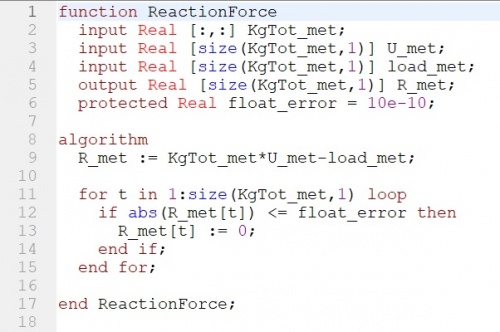
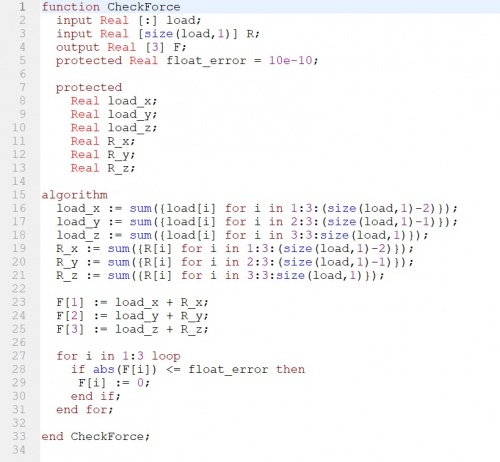
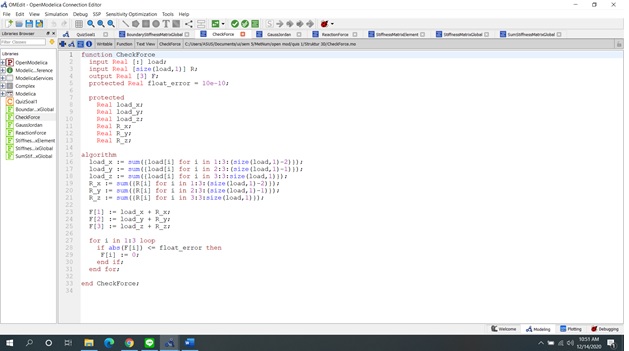
Check force mengecek apakah gaya yang terjadi pada suatu titik =0. Dalam check force fungsi fos agak berbeda sedikit karena terdapat beberapa angka titik 2 pada algorithm, contoh : Dari pers ini : [ F1x, F1y,..., Fnx, Fny] Load_x :=sum({load[i] for I in 1:3: (size(load,1)-2)}) 1:3:(size…) = angka mula : interval : angka akhir (dikurang 1 karena yang diminta angka ganjil.
Pertemuan 6, Senin 14 Desember 2020
Pada pertemuan hari ini, Pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai.
Pertemuan 7, Senin 21 Desember 2020
Pertemuan ini Kuliah diajarkan tentang aplikasi metode numerik dalam kasus optimasi bersama asisten dosen bu Candra. yang dimaksudkan dengan kasus optimasi adalah, penerapan peng-optimasi-an design menggunakan open modelica. optimasi yang dimaksud adalah untuk mendapatkan material yang tepat dengan harga yang murah untuk rangka sederhana.Praktik yang dilakukan adalah Bracket Optimization Using Golden Ratio Method.
Setelah itu dilakukan praktik optimasi dengan kasus sebagai berikut :
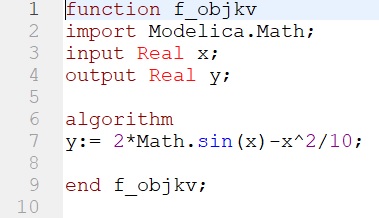
Tentukan nilai f(x) maksimum dari fungsi berikut dengan metode golden ratio :
f(x) = 2 sin x-x^2/10
Dari fungsi diatas diminta untuk menentukan nilai fungsi maksimum dari fungsi tersebut.
untuk fungsi panggilnya :
TUGAS BESAR, Optimasi truss
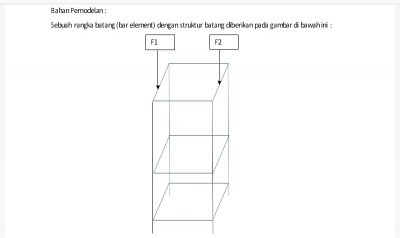
Dalam tugas besar ini kami diminta untuk menyelesaikan persoalan optimasi pada suatu struktur untuk mendapatkan harga terendah dengan optimasi maksimal. Diketathui sebuah struktur sebagai berikut :
Kondisi :
- Rangka batang
- 0,6 m x 0,75 m x 1,8 m (p x l x t)
- F1 = 2000 N
- F2 = 1000 N
Dalam pengerjaan tugas besar ini profil struktur yang igunakan adalah siku. dan karena saya belum sepenuhnya memahami tentang bahasa pemrograman, untuk sementara saya mengerjakan dengan menggunakan coding yang sudah disepakati bersama yakni coding kolaborasi buuatan Josiah, Ahmad Fahmi, dan Christo.
Alur kerja :
Untuk alur kerja seccara garis besar di rumuskan sebagai berikut :
Asumsi
1. Beban hanya terdistribusi pada titik sambung
2. safety factor minimal 2, atau setengah dari modulus elastisitas material
3. Batas displacement pada truss paling atas sebelum buckling bernilai 0,001 m.
4. Ketinggian trusses pada setiap lantai konstan, sebesar 0,6 m.
Metodologi
Dalam tugas besar ini ada 2 metode yang digunakan yaitu pada saat material sama dan pada saat cross section areanya sama.
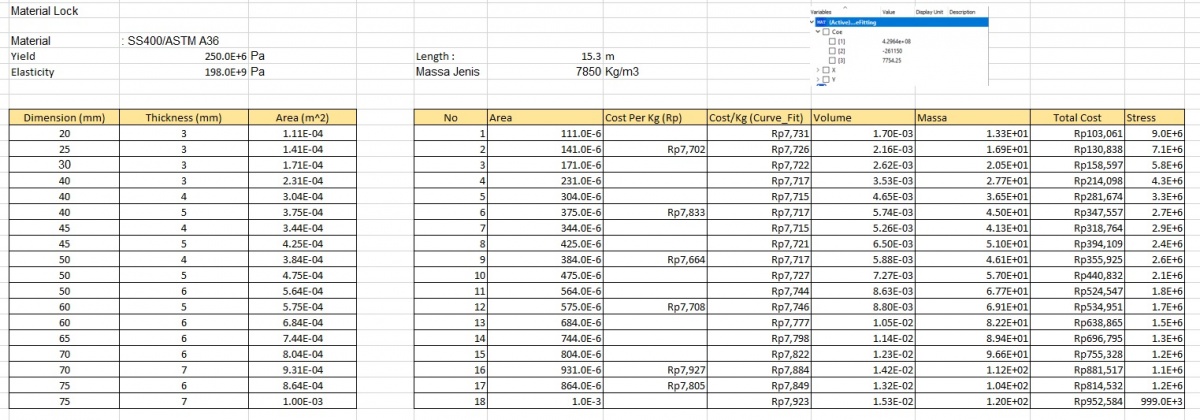
A) Elasticity Locked
1. Mencari data property dari material yang ingin digunakan seperti modulus elastisitas, dan yield strength (digunakan ...
2. Mencari harga dari material yang telah ditentukan sesuai ukuran yang tersedia di pasaran.
3. Memilih ukuran material yang akan dibandingkan sesuai dengan ukuran yang tersedia di pasaran (tebal yang dianjurkan 3 mm)
4. Menghitung nilai safety factor
5. Membuat rasio antara safety factor dengan totoal cost
6. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
7. Melakukan optimasi dengan menggunakan coding metode golden ratio
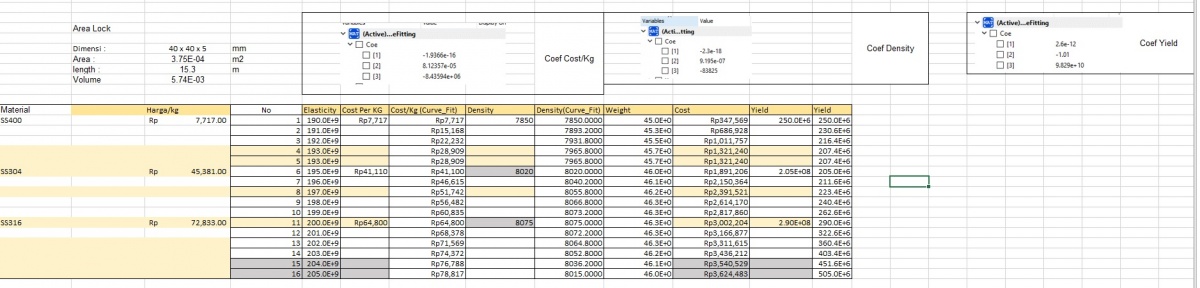
B) Cross Section Area Locked
1. Mendefinisikan luas penampang yang sama untuk seluruh variasi material >> 3,75 x 10^-4 m^2.
2. Mencari harga untuk 3 jenis variasi material >> SS400, SS304, SS316.
3. Menghitung nilai safety factor pada 3 variasi truss.
4. Membuat rasio antara safety factor dengan total cost.
5. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
6. Melakukan optimasi menggunakan metode golden section.
Coding
Pertama yang dilakukan adalah menentukan displacement, reaction force, stress, & safety factor:
|
model Trusses_3D_Tugas_Besar_Safety //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
parameter Integer C[:,2]=[1,5; 2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 -0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]= {0,0,0, 0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real safety[Trusses]; Real dis[3]; Real Str[3];
parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
//Creating Global Matrix G:=id; for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star; end for; //Implementing boundary for x in 1:Points loop if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for; //Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); for i in 1:3 loop check[i] := if abs(check[i])<=ers then 0 else check[i]; end for; //Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); end for; //Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for; //Safety factor for i in 1:Trusses loop if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if; end for; end Trusses_3D_Tugas_Besar_Safety; |
KALKULASI COE UNTUK CURVE-FITTING VIA OPENMODELICA
Program untuk curve fitting
Model
model callcurve
parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4};
parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
Function
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting;
Program untuk optimasi
Program untuk optimasi menggunakan metode golden ratio method
model Opt_Gold
parameter Real[3] y={-834.974,0.356007,2.39937e-5};
parameter Real xlo=111e-6;
parameter Real xhi=3.75e-4;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil Perhitungan dan Pembahasan
Karena coding di atas dan beberapa coding lainnya tidak dapat disimulasikan, maka digunakan data yang sudah dibahas bersama pada suatu kelompok.
Berikut adalah hasil perhitungan
Hasil Elasticity Locked
- Cara mencari cost per 6m, langkah pertama adalah menentukan cost/kg
Coe 1, 2, 3 --> untuk menentukan cost/kg dari daftar harga yang belum ada menggunakan Curve fitting method
Pada coding model curve fitting untuk mencari Coe, terdapat variable X yang diisi sebagai area dan Y sebagai harga yang diketahui
Setelah Coefisien 1,2,3 didapatkan digunakan rumus berikut untuk menentukan cost/kg setelah curve fitting :
cost/kg (6m) = (Coe1*(area^2)) + (Coe2*area) + Coe3
- length didapatkan dari total panjang besi siku yang dibutuhkan untuk membuat kerangka.
- Rumus untuk mencari area : A = (dimensi^2-(dimensi-tebal)^2)
- Total cost = (total panjang/6)*cost per 6 meter
- Stress : 1000/area
- Safety factor : Yield/stress
- Ratio safety / harga
Hasil Cross Section Area Locked
Program untuk optimasi
Program untuk optimasi menggunakan metode golden ratio method
model Opt_Gold
parameter Real[3] y={-834.974,0.356007,2.39937e-5};
parameter Real xlo=111e-6;
parameter Real xhi=3.75e-4;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for; end Opt_Gold;
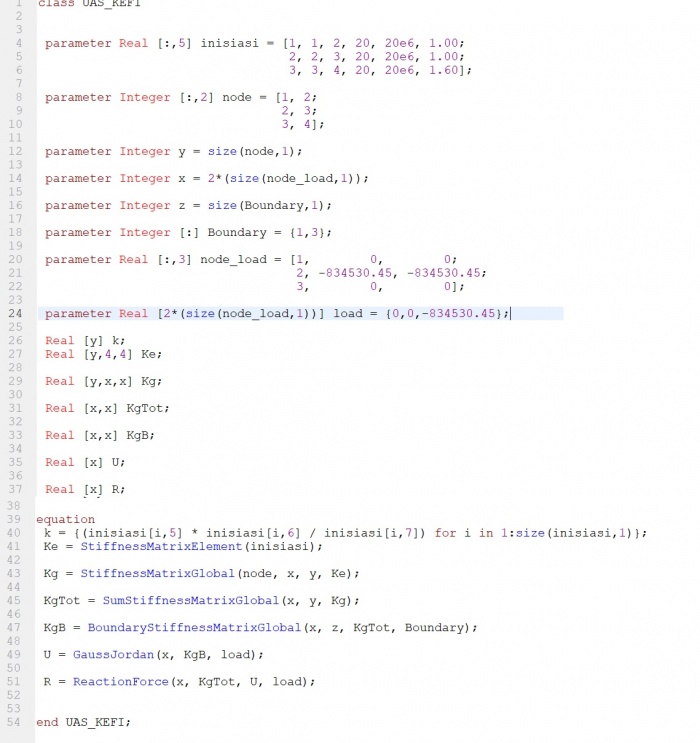
Jawaban UAS
Keterangan :
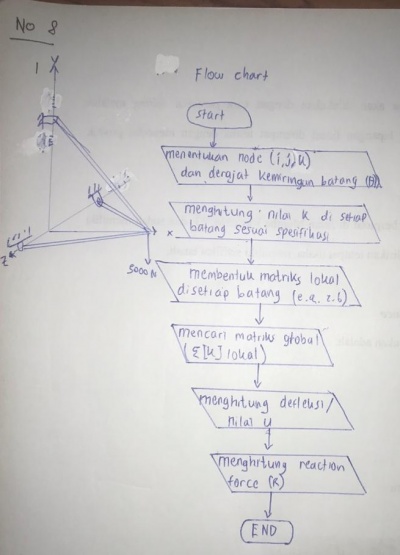
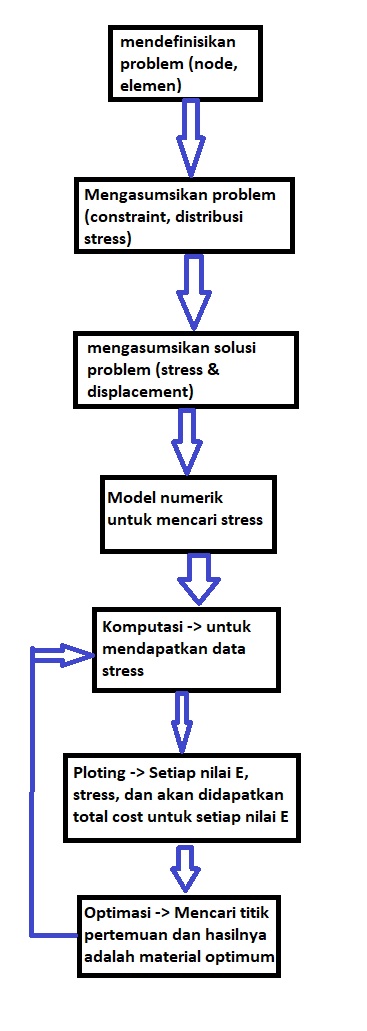
1) Flowchart permodelan numerik untuk optimasi struktur
2) Tujuan, Hukum fisika, dan asumsi yang akan digunakan
3) Nilai E, A load, dan length adalah nilai asumsi
4) Urutan langkah-langkah perhitungan matrix kesetimbangan global dari no 3. + pengecekan kesalahan
5) Fungsi dan constrain untuk optimasi struktur.
6) Asumsi nilai parameter
7) Coding open modelica (tidak bisa running)