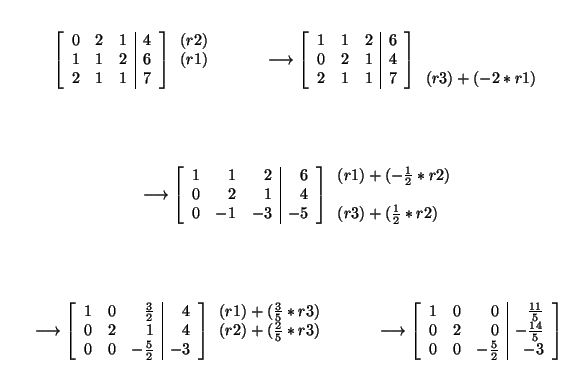Kelompok 5
Kelompok 5
-Aulia Rifai
-Adriel Aaron
-Adim
Dalam post ini, kelompok kami akan menjelaskan mengenai eliminasi Gauss-Jordan menggunakan program Phyton. Dalam aljabar linear, eliminasi Gauss-Jordan adalah algoritme versi dari eliminasi Gauss. Pada metode eliminasi Gauss-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (Semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).
Metode eliminasi Gauss-Jordan kurang efisien untuk menyelesaikan sebuah SPL, tetapi lebih efisien daripada eliminasi Gauss jika kita ingin menyelesaikan SPL dengan matriks koefisien sama.
Motede tersebut dinamai Eliminasi Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Wilhelm Jordan.
Untuk codingnya, kami menggunakan sebagai berikut
def printMatrixline(M):
for x in range(lenX):
for y in range(lenY):
print("M[" + str(x) + "," + str(y) + "]: " + str(M[x][y]))
def printMatrixform(M):
for x in range(lenX):
for y in range(lenY):
print(str(M[x][y]) + " ", end = )
print("\n")
print("Insert row: ")
lenX = int(input())
print("insert column: ")
lenY = int(input())
M = [[0 for x in range(lenY)] for y in range(lenX)]
if lenY - 1 != lenX:
print("Your matrix cannot be used.")
else:
#input matrix
for x in range(lenX):
for y in range(lenY):
print("M[" + str(x) + "," + str(y) + "]: ")
M[x][y] = int(input())
print("\n")
#printMatrixline(M)
printMatrixform(M)
print("\n")
flag = 0
n = lenX
for i in range(n):
if M[i][i] == 0:
c = 1
while M[i + c][i] == 0 and (i + c) < n:
c += 1
if (i + c) == n:
flag = 1
break
j = i
for k in range(n + 1):
temp = M[j][k]
M[j][k] = M[j + c][k]
M[j + c][k] = temp
for j in range(n):
if i != j:
p = M[j][i] / M[i][i]
for k in range(n + 1):
M[j][k] = M[j][k] - (M[i][k]) * p
printMatrixform(M)
for i in range(n):
if M[i][i] != 1:
p = M[i][i]
M[i][n] = M[i][n] / p
M[i][i] = M[i][i] / p
print("\n")
printMatrixform(M)
untuk membuktikan, kami menggunakan matrix 3x4 =
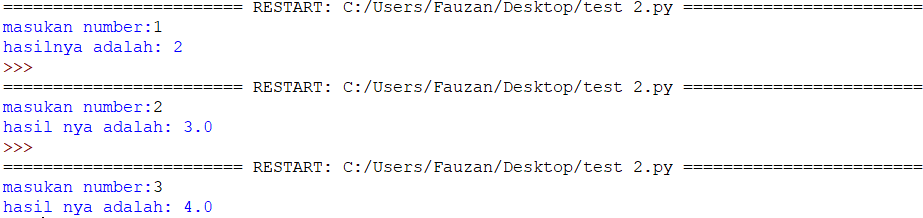
kemudian, menggunakan Coding menghasilkan hasil sebagai berikut
Karena hasil soal dan pembuktian sama, maka bisa disimpulkan program coding phyton benar
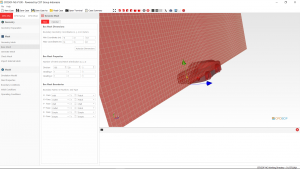
CFDSOF
Pada tugas CFDSOF kali ini, kelompok kami mencoba untuk menganalisis drag pada mobil dengan menggunakan software CFDSOF. Namun, ketika kami ingin generate mesh, program CFDSOF tidak dapat generate mesh sehingga kami tidak dapat melanjutkan tugas ini.