Kelompok 3
Perkenalkan, Kami dari kelompok 3 dengan anggota
1. Candra Steven
2. Fahmi Ismail Wibisono
3. Wildan Zulfa Abdurrohman
Contents
Metode Eliminasi Gauss
Eliminisasi Gauss adalah metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Dengan melakukan operasi baris sehingga matriks tersebut menjadi salah satu metode penyelesaian persamaan linear.
Contoh soal
Pengerjaan Matematis
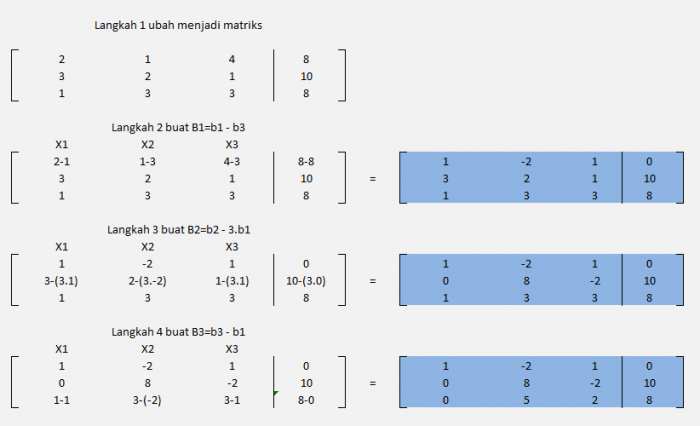
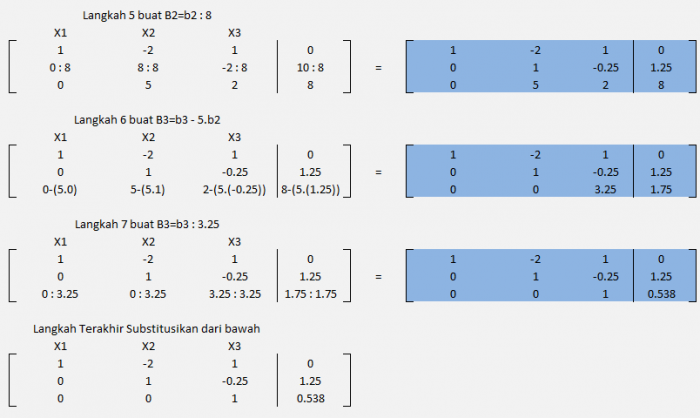
Menggunakan Eliminasi Gauss
Kemudian menyelesaikan dengan Subtitusi
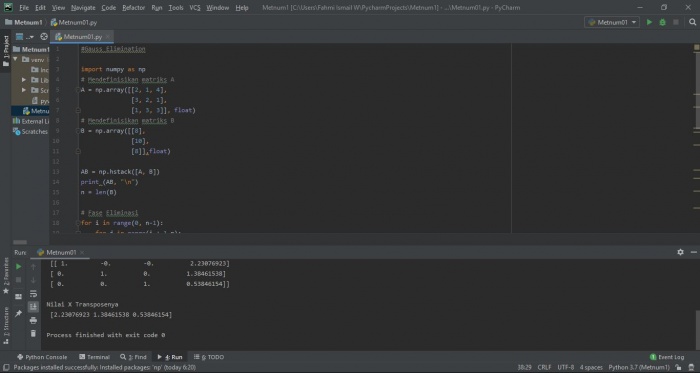
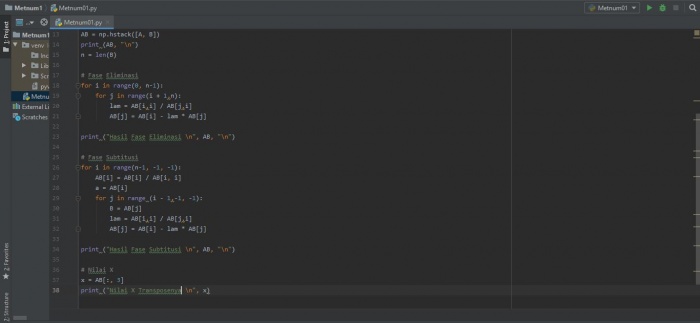
Pengerjaan Menggunakan Bahasa Python
Dalam penggunaan matriks pada bahasa python dibutuhkan fungsi array dengan cara import numpy
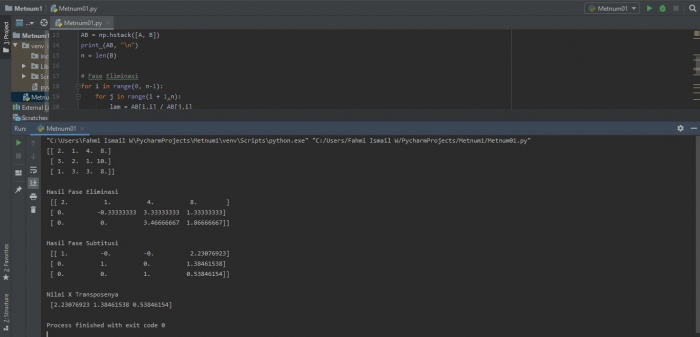
Hasil perhitungan dengan Python
Program Python
Runge Kutta
Pada tanggal 9 Oktober 2019, kami diberikan tugas untuk membuat persamaan pegas dengan metode Runge Kutta. Soalnya adalah sebagai berikut
Penyelesaian dari soal ini dapat diselesaikan dengan coding sebagai berikut
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Mohon masukkan nilai t positif.")
Tugas Simulasi CFD Pada Mobil
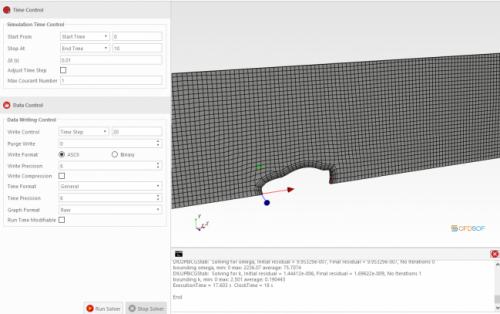
Tugas ini merupakan tugas untuk melakukan simulasi aliran udara pada permukaan mobil untuk mendapatkan nilai drag force menggunakan software CFDSOF-NG. CFDSOF-NG merupakan aplikasi berbasis metode numerik yang berfungsi untuk menganalisa aliran fluida pada suatu permukaan benda. Langkah-langkah untuk melakukan analisis CFD menggunakan CFDSOF-NG adalah sebagai berikut:
1. Mengimport file .stl ke dalam software CFDSOF-NG
2. Membuat mesh dari file .stl
3. Run solve pada software CFDSOF-NG
4. Melakukan analisis lebih lanjut dengan menggunakan software paraview
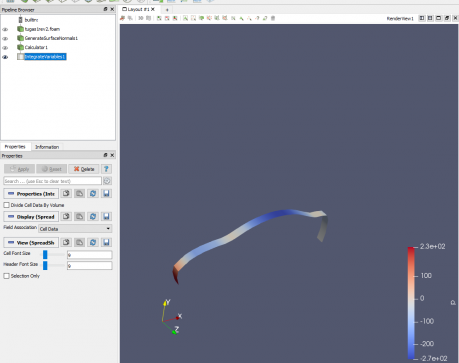
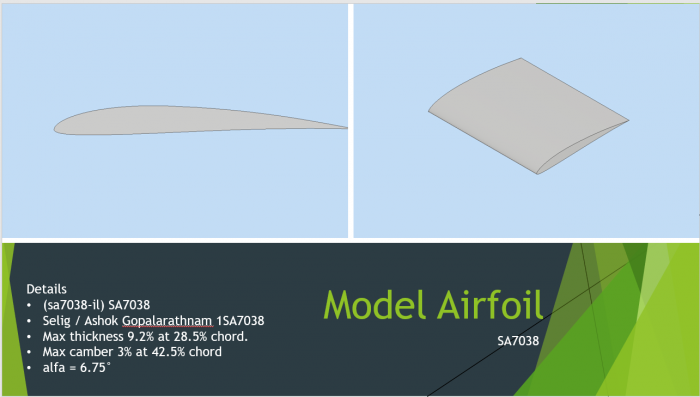
Tugas Optimasi CFD Airfoil
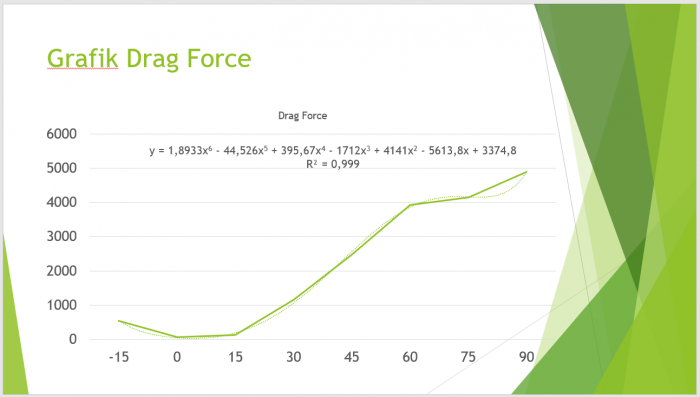
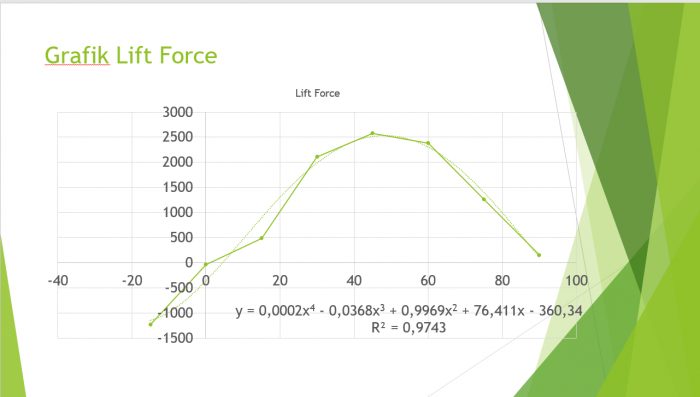
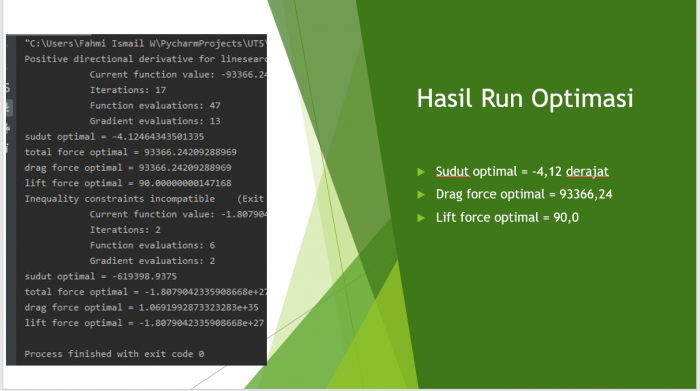
Tugas ini mengenai optimasi pada airfoil menggunakan metode numerik. Mula-mula kami melakukan analisis menggunakan CFDSOF-NG untuk mendapatkan nilai lift force dan drag force. Setelah itu didapatkan grafik berdasarkan setiap perubahan AoA. Kemudian dilakukan optimasi dengan metode numerik untuk mendapatkan nilai maksimal dari gaya drag dan lif berdasarkan AoA. Berdasarkan hasil optimasi didapatkan hasil berupa sudut optimal dari pesawat yang mana akan meningkatkan performa dan meminimalisir gaya gesekan.
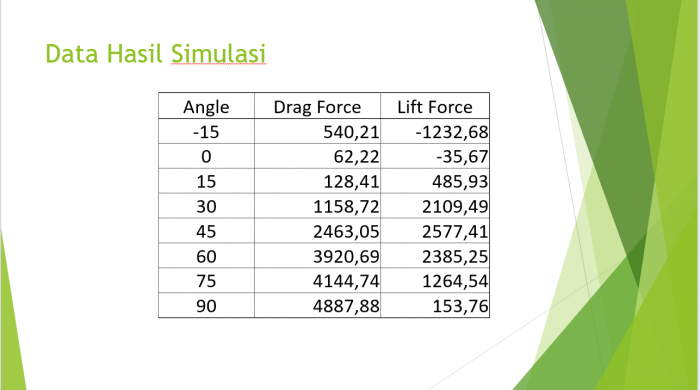
Kemudian kami diberikan tugas mengenai simulasi airfoil dengan menggunakan airfoil buatan sendiri ataupun airfoil yang sudah ada. Simulasi dilakukan dengan merubah sudut Angle of Attack (AoA) dalam kecepatan tertentu. AoA yang digunakan mulai dari -15 derajat sampai 90 derajat, dengan increment 15 derajat. Tugas ini nantinya akan dipresentasikan pada pertemuan selanjutnya, sehingga harus dibuat dalam bentuk powerpoint.
Silahkan berkomentar pada kolom di bawah
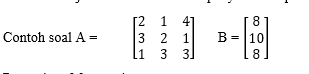









Enable comment auto-refresher