Farhan Rizqi Syahnakri
Contents
Biodata Diri
Nama : Farhan Rizqi Syahnakri
NPM : 1906379081
Prodi : Teknik Mesin S1 Reguler
TTL : Jakarta, 2 Februari 2001
Angkatan : 2019
Saya memilih untuk menjadi bagian dari Fakultas Teknik khususnya pada program pendidikan Teknik Mesin karena saya ingin mengembangkan diri, baik dari segi akademis maupun non akademis. Memasuki tahun kedua saya berkuliah, saya merasa ketertarikan saya akan dunia Teknik Mesin semakin tinggi, ditambah dengan banyak hal yang telah saya dapatkan dari non akademis yang sangat bisa saya manfaatkan untuk pengembangan soft skill saya kedepannya. Saya sangat bersyurukur atas nikmat Tuhan Yang Maha Esa dengan segala pemberian nikmat terhadap makhluknya. Besar harapan saya untuk dapat menjadi manusia yang berguna bagi bangsa, negara, agama dan khususnya lingkungan sekitar saya.
Metode Numerik
Metode Numerik adalah teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan cara operasi hitungan. Dalam metode numerik ini dilakukan operasi hitungan dalam jumlah yang banyak dan prosesnya berulang. Sehingga dalam prakteknya perlu bantuan komputer untuk menyelesaikan hitungan tersebut. Dalam kehidupan sehari-hari, metode numerik adalah salah satu tools yang sangat bermanfaat dan membantu kita dalam melakukan pekeraan yang berhubungan dengan matematis.
Pada kelas Metode Numerik-02 semester ganjil 2020/2021 sampai dengan UTS, perkuliahan diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Dimana pada pertemuan yang telah dilakukan telah membahas materi seperti:
- Pseudocode
- Sistem Persamaan dengan metode Newton Rhapson, Sekan, dan Biseksi
- Turunan Numerik
- Deret Taylor dan McClaurin
- Regresi Linear
- Interpolasi
Pembelajaran selanjutnya sampai dengan UAS akan dilanjutkan oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Review Pertemuan
Pertemuan Minggu 1
Pada pertemuan minggu pertama pada hari Rabu, 11 November 2020 saya dijelaskan beberapa tujuan dalam kita mempelajari metode numerik :
1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik. Contoh : Persamaan aljabar, algoritma, pencocokan kurva, persamaan diferensial parsial, dll.
2. Mengerti aplikasi dari belajar metode numerik
3. Mampu menerapkan metode numerik dalam persoalan keteknikan
4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab
Selain itu juga pada minggu ini juga mencoba mensimulasikan perangkat lunak OpenModelica dalam kegunaannya untuk menyelesaikan suatu sistem persamaan.
Tugas Minggu 1
Berikut adalah link tutorial menggunakan OpenModelica yang telah saya buat berdasarkan pembelajaran minggu 1
Pertemuan Minggu 2
Pada pertemuan minggu ke-2 ini dimulai dengan mempresentasikan tugas yang diberikan di minggu kemarin oleh beberapa mahasiswa. disela-sela presentasi kami juga membahas mengenai fitur class function dan dijelaskan alasan mengapa menggunakan aplikasi open modellica sebagai media untuk mempelajari metode numerik. Jawaban dari pertanyaan tersebut adalah karena aplikasi open modellica lebih mudah untuk digunakan di berbagai perangkat ( tidak harus perangkat dengan spesifikasi tinggi ) dan yang paling penting lagi murah.
Tugas Minggu 2
Berikut adalah link tutorial menggunakan OpenModelica yang telah saya buat berdasarkan pembelajaran mengenai open class function pada pertemuan minggu 2
Tugas Minggu 3
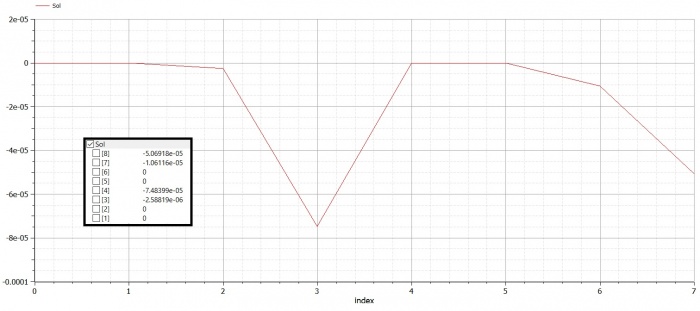
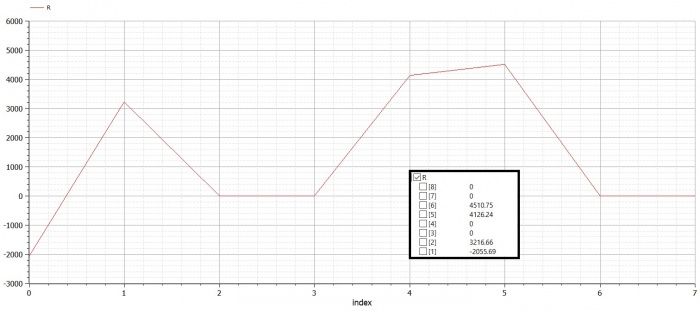
Berikut 2 contoh penggunaan aplikasi Modelica untuk menyelesaikan perhitungan displacement dan reaction force pada trusses:
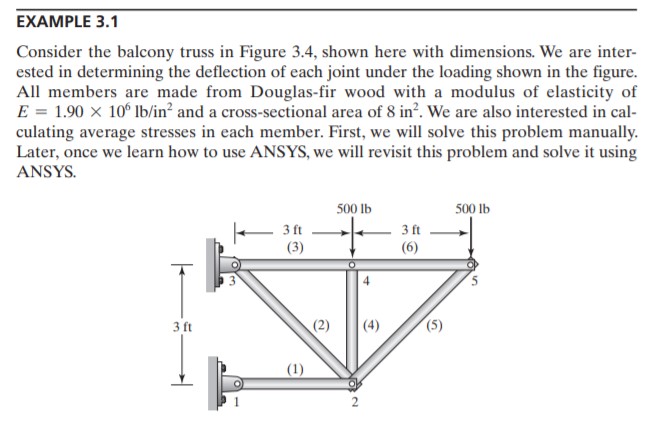
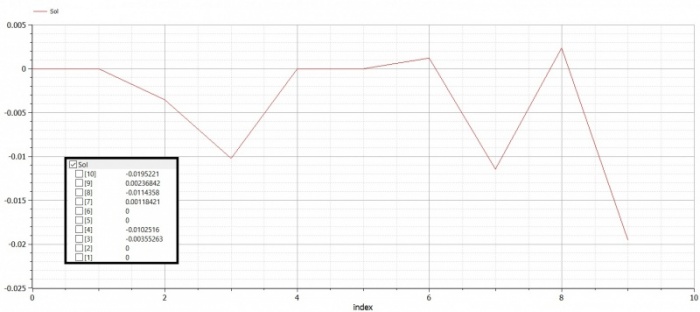
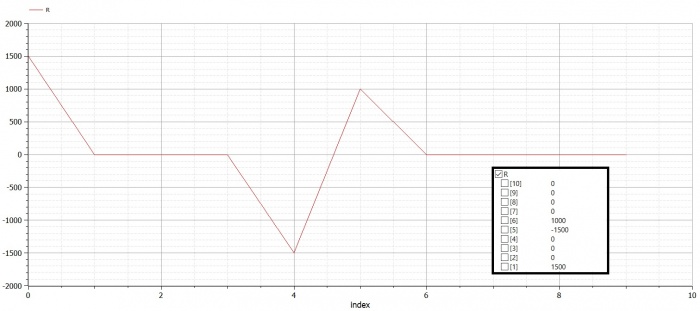
Trusses Problem 1 (Example 3.1)
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
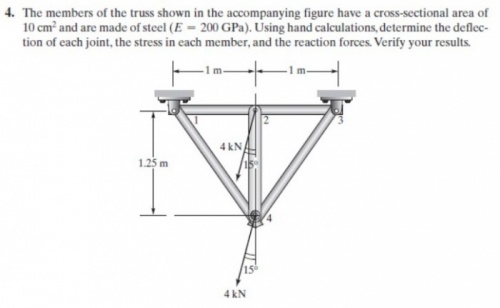
Trusses Problem 2 (Homework)
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
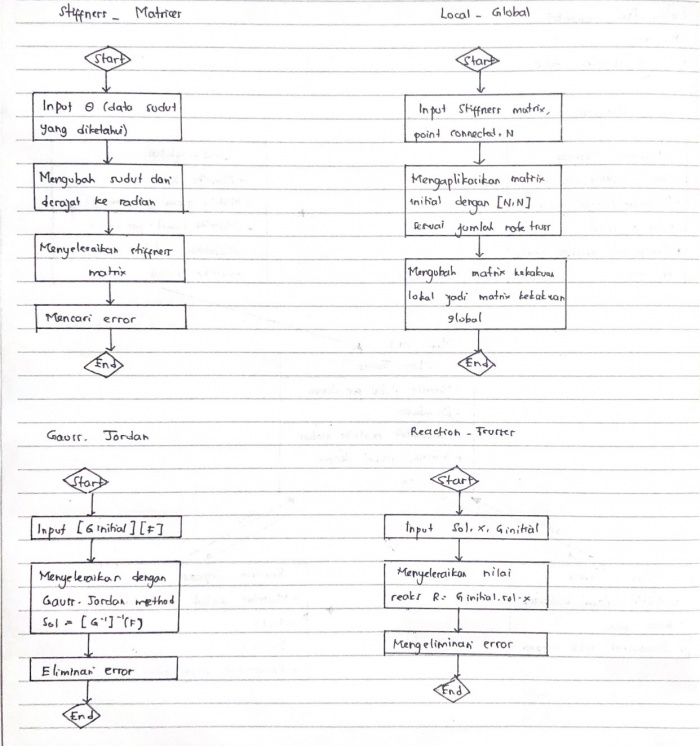
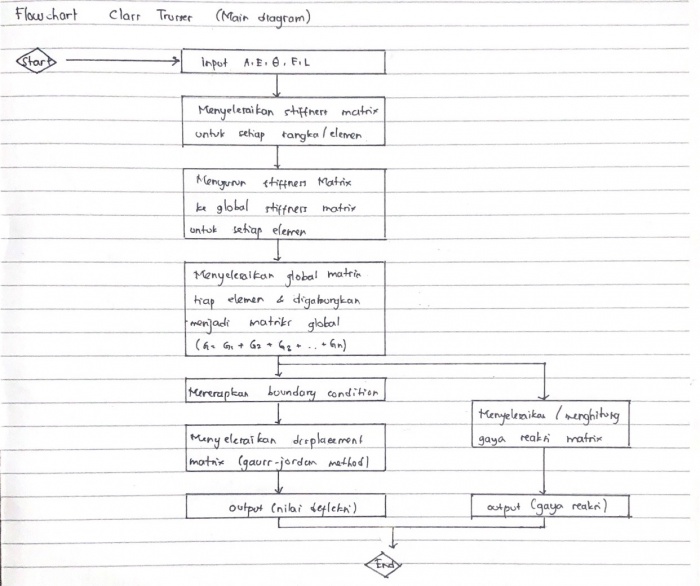
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; Gauss Jordan function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; Bold textoutput Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end Gauss_Jordan; |
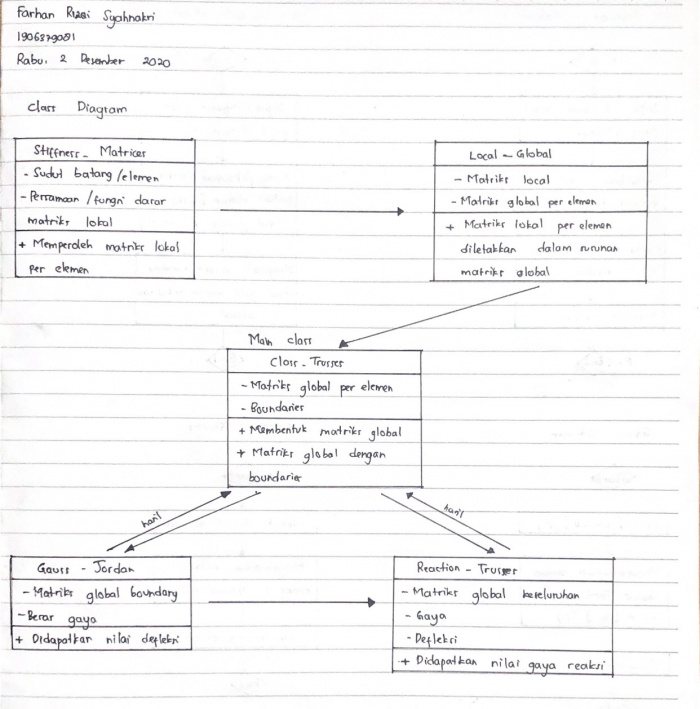
Pertemuan Minggu 4
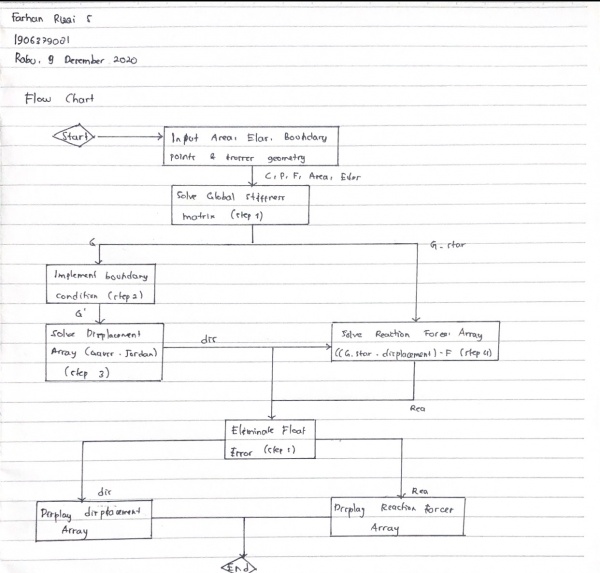
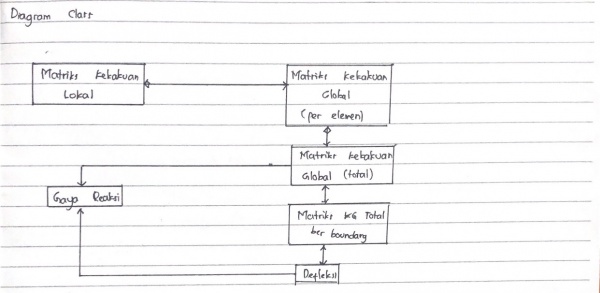
Pada tanggal 2 Desember 2020, saya melakukan kuis membuat class diagram dan flowchart untuk coding dari Josiah Enrico. Berikut adalah hasil dari pengerjaan kuis saya :
Tugas Minggu 4
|
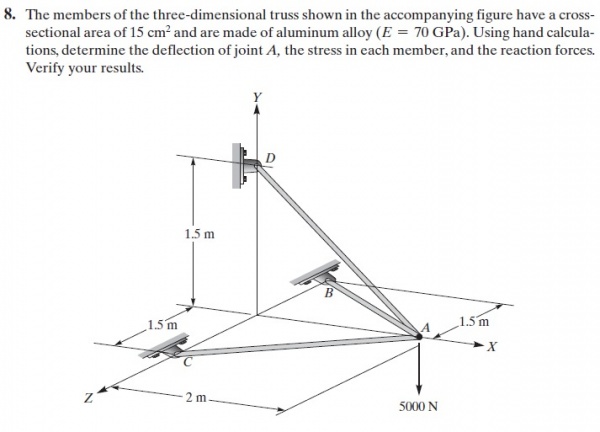
Master class Trusses3D
//define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Area=0.0015; //Area
parameter Real Elas=70e9; //Elasticity
//define connection
parameter Integer C[Trusses,2]=[1,2;
1,3;
1,4];
//define coordinates (please put orderly)
parameter Real P[Points,3]=[2,0,0;
0,0,1.5;
0,0,-1.5;
0,1.5,0];
//define external force (please put orderly)
parameter Real F[Points*3]={0,-5000,0,
0,0,0,
0,0,0,
0,0,0};
//define boundary
parameter Integer b[:]={2,3,4};
//solution
Real displacement[N], reaction[N];
protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, E, X[3,3];
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Constant
L:=Modelica.Math.Vectors.length(q2-q1);
E:=Area*Elas/L;
//Solving Matrix
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=E*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
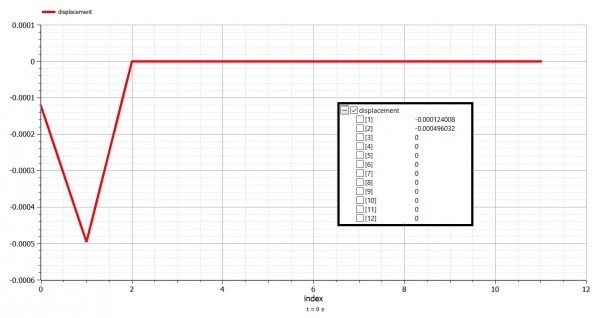
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
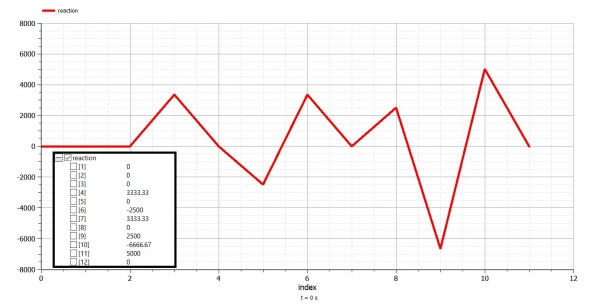
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
end Trusses3D;
|
Pertemuan Minggu 5 (Pengganti)
Pada pertemuan minggu ke-5, kami diajarkan untuk melakukan muhasabah terhadap penilaian diri sendiri mengenai materi Metode Numerik yang sudah diberikan oleh Pak Dai. Setelah itu kami juga diajarkan mengenai sistem trusses dengan metode belajar kelompok bersama kelas Metnum 2 dan Metnum 3.
Pertemuan Minggu 6
Pada pertemuan kali ini kami diajarkan mengenai optimasi menggunakan Open Modelica. Optimasi sendiri adalah sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.
Selanjutkan Bu Chandra mengajarkan langsung, dengan menggunakan Software Open MOdelica. Kita dapat membuat sebuah fungsi pada awalnya:
Fungsi panggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
Tugas Besar Metnum
Pada tugas besar ini, diminta untuk melakukan optimasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini
Asumsi yang digunakan untuk melakukan perhitungan ini antara lain:
1. Variasi Stiffness terikat dengan variabel area pada material yang akan digunakan. Karean akan sulit apabila memvariasikan elastisitas, dimana setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya
2. Dimensi material mengikuti standar ukuran material yang dipilih
3. Beban akan terdistribusi hanya pada node/point penghubung (karena bersifat trusses)
4. Terdapat 2 perhitungan yaitu dengan material lock dan area lock.
Flow Chart
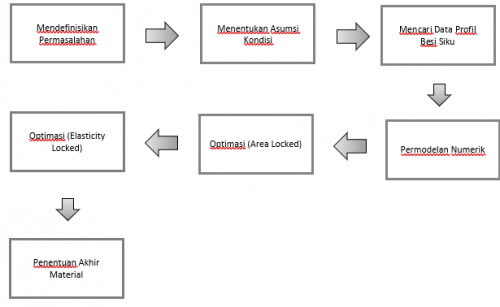
Untuk mengerjakan tugas besar ini, saya membuat flowchart alur pengerjaan untuk memudahkan peengerjaan saya. Berikut adalah flowchart yang saya buat
Mendefinisikan Permasalahan
Melakukan optimisasi pada rangka untuk mengetahui material apa yang memiliki kekuatan yang maksimal dengan harga yang minimum. Pertama-tama kita harus mengetahui profil dari besi siku dan rangka yang digunakan. Setelah itu kita juga harus menentukan elemen serta node pada rangka.
Menentukan Asumsi dan Kondisi
Asumsi:
- Diasumsikan tidak ada bending karena bersifat truss - Beban terdistribusi pada node - Safety Factor = 2 - Batas displacement 0,001m sebelum terjadi buckling - Variabel bebas
Constraint" - Node 1,2,3,4 (lantai dasar) fixed - Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga: 1. Node 13 & 16 = 1000N 2. Node 14 & 15 = 500N
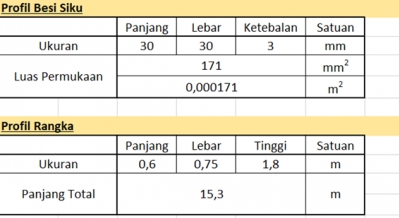
Research Data Profil Besi Siku
Pemodelan Numerik
|
3D Trusses Model //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) parameter Real Area= (nilai area) ; //Luas Besi Siku (Dimension=30x30x3mm) parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) //define connection
parameter Integer C[:,2]=[1,5; // (Elemen 1)
2,6; // (Elemen 2)
3,7; // (Elemen 3)
4,8; // (Elemen 4)
5,6; // (Elemen 5)
6,7; // (Elemen 6)
7,8; // (Elemen 7)
5,8; // (Elemen 8)
5,9; // (Elemen 9)
6,10; // (Elemen 10)
7,11; // (Elemen 11)
8,12; // (Elemen 12)
9,10; // (Elemen 13)
10,11;// (Elemen 14)
11,12;// (Elemen 15)
9,12; // (Elemen 16)
9,13; // (Elemen 17)
10,14;// (Elemen 18)
11,15;// (Elemen 19)
12,16;// (Elemen 20)
13,14;// (Elemen 21)
14,15;// (Elemen 22)
15,16;// (Elemen 23)
13,16];//(Elemen 24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar;
|
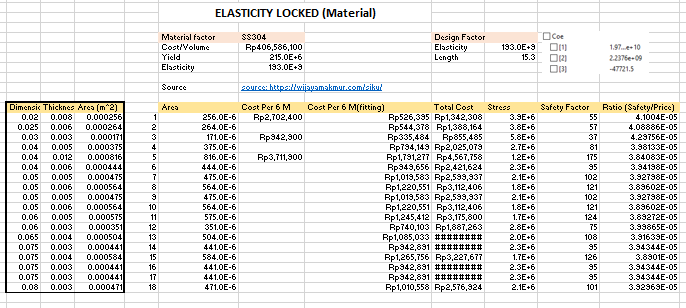
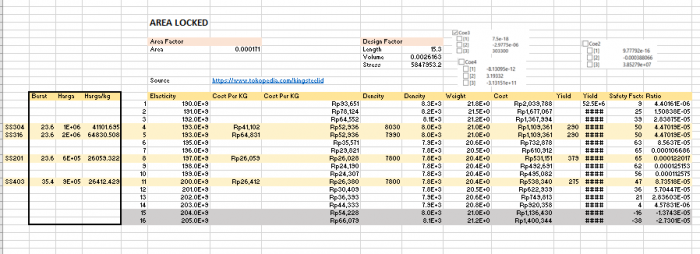
Pencarian Data Material
Untuk melakukan pencarian data, saya akan melakukan Elasticity Locked dan Area Locked Material
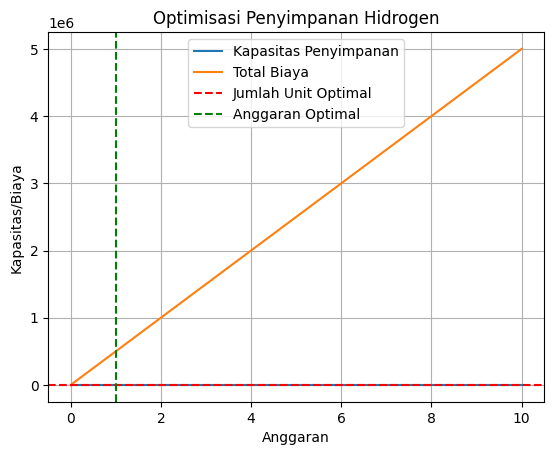
Berikut adalah grafik yang saya dapatkan
Curve Fitting
Berikut adalah function curve fitting yang saya gunakan
Ini adalah function panggil terhadap curve fitting yang saya gunakan
Berikut adalah grafik hasil dari curve fitting dan material yang saya gunakan
UAS Metoda Numerik-02
Berikut adalah soal UAS Metoda Numerik yang diberikan oleh Pak Dai :
Ujian Akhir Semester Metoda Numerik Semester Gasal 2021 Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut. 1. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut. 2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan 3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D). a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal) b) Matriks kesetimbangan global 4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya 5. Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut 6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas 7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6
Berikut adalah jawaban dari UAS Metoda Numerik yang telah saya selesaikan :
Untuk mengerjakan soal nomor 7, kami diminta menyelesaikannya menggunakan Aplikasi Open Modelica. Berikut adalah hasil jawaban saya menggunakan Aplikasi Open Modelica.
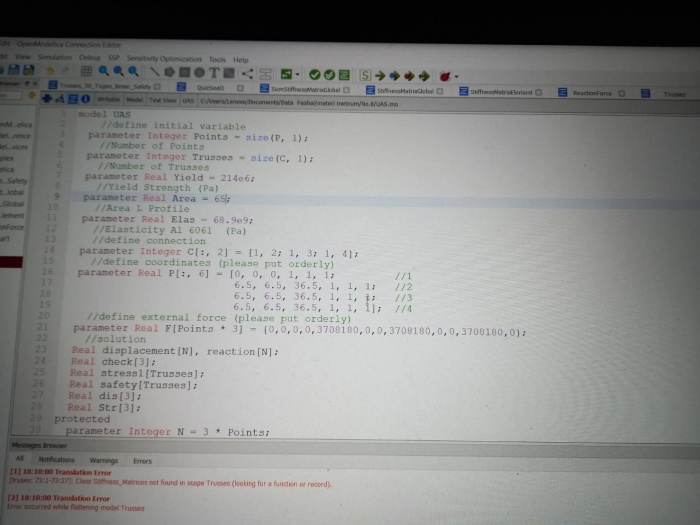
model UAS
//define initial variable
parameter Integer Points = size(P, 1);
//Number of Points
parameter Integer Trusses = size(C, 1);
//Number of Trusses
parameter Real Yield = 214e6;
//Yield Strength (Pa)
parameter Real Area = 65;
//Area L Profile
parameter Real Elas = 68.9e9;
//Elasticity Al 6061 (Pa)
//define connection
parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4];
//define coordinates (please put orderly)
parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1
6.5, 6.5, 36.5, 1, 1, 1; //2
6.5, 6.5, 36.5, 1, 1, 1; //3
6.5, 6.5, 36.5, 1, 1, 1]; //4
//define external force (please put orderly)
parameter Real F[Points * 3] =
{0,0,0,0,3708180,0,0,3708180,0,0,3708180,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N = 3 * Points;
Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] =
identity(N), cx, cy, cz, L, X[3, 3];
Real err = 10e-10, ers = 10e-4;
algorithm
//Creating Global Matrix
G := id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy
* cz; cz * cx, cz * cy, cz ^ 2];
g := zeros(N, N);
for m, n in 1:3 loop
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n];
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n];
end for;
G_star := G + g;
G := G_star;
end for;
//Solving Matrix
//Transforming to global matrix
//Implementing boundary
for x in 1:Points loop
if P[x, 4] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 2, a] := 0;
G[x * 3 - 2, x * 3 - 2] := 1;
end for;
end if;
if P[x, 5] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 1, a] := 0;
G[x * 3 - 1, x * 3 - 1] := 1;
end for;
end if;
if P[x, 6] <> 0 then
for a in 1:Points * 3 loop
G[x * 3, a] := 0;
G[x * 3, x * 3] := 1;
end for;
end if;
end for;
//Solving displacement
displacement := Modelica.Math.Matrices.solve(G, F);
//Solving reaction
reaction := G_star * displacement - F;
//Eliminating float error
for i in 1:N loop
reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i];
displacement[i] := if abs(displacement[i]) <= err then 0 else
displacement[i];
end for;
//Checking Force
check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in
1:3:N - 2});
check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in
2:3:N - 1});
check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in
3:3:N});
for i in 1:3 loop
check[i] := if abs(check[i]) <= ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3
* (C[i, 2] - 1) + j]);
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz;
cz * cx, cz * cy, cz ^ 2];
Str := X * dis;
stress1[i] := Modelica.Math.Vectors.length(Str);
end for;
//Solving Matrix
//Safety factor
for i in 1:Trusses loop
if stress1[i] > 0 then
safety[i] := Yield / stress1[i];
else
safety[i] := 0;
end if;
end for;
end UAS;