Persamaan Konservasi
Revision as of 11:11, 7 February 2019 by Amalinadhi.cahya (talk | contribs) (Created page with "== Governing Equations == Penyelesaian kasus aliran fluida diatur oleh persamaan atur (''governing equations'') yang terdiri atas 3 persamaan konservasi dasar properti fluida....")
Governing Equations
Penyelesaian kasus aliran fluida diatur oleh persamaan atur (governing equations) yang terdiri atas 3 persamaan konservasi dasar properti fluida. Persamaan konservasi tersebut antara lain:
- Konservasi massa.
Persamaan kontinuitas. - Konservasi momentum.
Hukum 2 Newton, perubahan momentum sama dengan jumlah seluruh gaya yang bekerja pada partikel fluida. - Konservasi energi.
Hukum 1 Termodinamika, laju perubahan energi sama dengan laju penambahan/pengurangan kalor (heat) atau kerja (work) pada partikel fluida.
Persamaan di atas menjelaskan bahwa massa, momentum, dan energi bernilai konstan dalam sistem tertutup. Sederhananya, Apa yang masuk, akan keluar di tempat lain. Tiga persamaan di atas akan menyelesaikan nilai dari v, p, dan T pada setiap titik dalam domain perhitungan.
Lagrangian dan Eularian
Untuk menyelesaikan governing equations pada aliran fluida yang bergerak, kita harus mengetahui bagaimana metode memandang dan mengidentifikasi pergerakan dari fluida tersebut. Ada dua metode umum yang biasa digunakan untuk memandang pergerakan fluida ini, Lagrangian dan Eularian.
Lagrangian
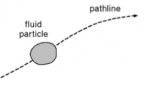
Medan aliran fluida dapat diibaratkan sebagai sekumpulan besar partikel fluida, yang berukuran cukup besar untuk dapat mendefinisikan properti fluida seperti massa, momentum, energi internal, dan properti fluida lainnya. Formulasi properti fluida dalam Lagrangian mengacu pada fungsi waktu. Untuk mendapatkan properti aliran fluida pada seluruh domain tersebut, kita mulai dari menghitung semua partikel fluida pada seluruh domain di awal waktu kemudian mengikuti pergerakan partikel tersebut hingga mencapai akhir.