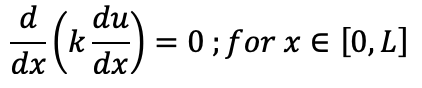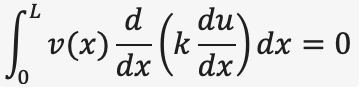User:Muhamad.akbar41

Nama saya Muhamad Akbar Fuad, nama panggilannya Akbar Bidang peminatan yang diambil adalah Sistem Otomasi dan Manufaktur, dengan topik penelitian Additive Manufacturing Systems.

BELAJAR KOMPUTASI TEKNIK DENGAN CHAT GPT

DAI5

Conscious Thinking (Think about Reality and How to Solve it all)

I(2) Intention
I(3) Initial Thinking
I(4) Idealization
I(5) Instruction Set

JILID 1 : 1-Dimensional Partial Differential Equation (PDE)

Question 1: Did you know about DAI5?

The DAI5 Framework is a structured method designed to support systematic problem-solving, particularly in engineering and technical analysis. Developed by Dr. Ahmad Indra Siswantara, the DAI5 framework consists of five main steps: defining the problem, analyzing causes, ideating solutions, implementing, and evaluating outcomes. This approach is often applied in complex scenarios like numerical simulations, finite element analysis, and stress testing within engineering fields. By using DAI5, users aim to ensure each phase is rigorously analyzed to optimize solutions and outcomes, as demonstrated in various technical case studies on topics such as fluid dynamics and pipe stress analysis.

Question 2: Can you derive finite element equations from 1D PDE governing equations using weighted residual in a very simple way along with an example?

Certainly! Deriving the finite element equations from a 1D partial differential equation (PDE) using the weighted residual method is a great way to understand the basics of the finite element method (FEM). Let’s go through it step-by-step with a simple example.

Problem Setup: 1D PDE Example Consider the 1D steady-state heat conduction equation with no internal heat generation:

where:

•	u(x) is the temperature field,
•	k is the thermal conductivity (assumed constant for simplicity),
•	L is the length of the domain.

Suppose we have the boundary conditions:

1.	u(0)=u0 (a Dirichlet boundary condition),
2.	du/dx = q at x = L (a Neumann boundary condition).

Step 1: Formulate the Weak Form (Weighted Residual Form) To derive the finite element equations, we start with the weak form of the governing equation. This involves:

1.	Multiplying the differential equation by a test function v(x),
2.	Integrating over the domain,
3.	Applying integration by parts to reduce the order of derivatives on u.

The weighted residual form is: