Fadil Naufal Wahas
Assalamu'alaikum Warahmatullahi Wabarakatuh, Salam Sejahtera untuk kita semua.
Perkenalkan, saya Fadil Naufal Wahas, NPM 2306185416, mahasiswa magister Departemen Teknik Mesin Universitas Indonesia.
Contents
Thesis
Tesis : Studi komputasi tentang pengaruh sifat fluida terhadap karakteristik counter-current flow limitation (CCFL) di 1/30 pressurized water reactor (PWR) hot leg
Thesis : Computational study of the effects of fluid properties on counter-current flow limitation (CCFL) characteristics in 1/30 pressurized water reactor (PWR) hot leg
Pembimbing : Prof. Dr. Ir. Harinaldi, M.Eng.
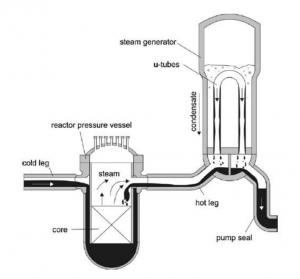
Pada kanal uap (hot leg) teras reaktor pada pembangkit listrik tenaga nuklir pressurized water reactor (PWR) terdapat fenomena counter-current flow limitation (CCFL) yang terjadi pada saat kondisi kecelakaan loss-of-coolant accident (LOCA).
Saat LOCA, karena adanya penurunan tekanan, terjadi penguapan air pendingin yang berada di reaktor sehingga uap tersebut mengalir ke steam generator (SG) melalui hot leg. Sebagian uap yang terkumpul di SG tersebut mengalami kondensasi menjadi air. Air tersebut, dipengaruhi gravitasi, mengalir kembali ke reaktor, berlawanan arah dengan uap. Aliran berlawanan arah ini terjadi saat kecepatan aliran uap berada di bawah ambang batas flooding atau counter-current flow limitation (CCFL).
Fenomena CCFL ini menjadi penting untuk diteliti karena berhubungan dengan keselamatan reaktor nuklir. Oleh karena itu, pengaruh sifat fisik fluida terhadap karakteristik CCFL perlu diinvestigasi.
DAI5 Framework
DAI5 Framework is a guideline developed by Dr. Ahmad Indra Siswantara for problem-solving processes. This video essay is my interpretation of the DAI5 Framework.
Computational Fluid Dynamics (CFD)
Convergence and Grid Independence
The two aspects that characterize a successful simulation result are convergence and grid independence. A converged solution have very small residuals – measures of the overall conservation of the flow properties.
The only way to eliminate errors due to coarseness of a grid is to perform a grid dependence study, which is a procedure of successive refinement of an initially coarse grid until certain key results do not change. Then the simulation is grid independent. A systematic search for convergent and grid-independent results forms an essential part of all high-quality CFD studies.
Reference: H. K. Versteeg and W. Malalasekera, An Introduction to Computational Fluid Dynamics: The Finite Volume Method. 2nd Edition. England: Pearson, 2007.
Cavity 2D Laminar Flow with CFDSOF
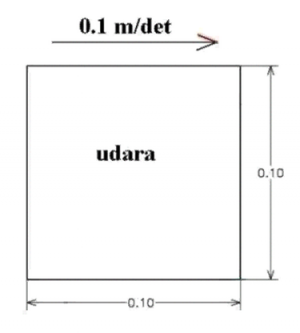
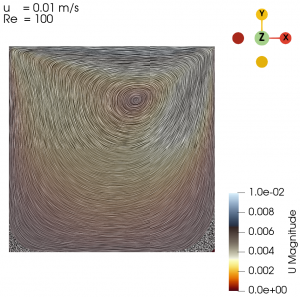
The image below shows a 0.1 m by 0.1 m cavity section filled with air (udara) where the upper wall is moving in the +x-axis direction at 0.1 m/s where the density (ρ) of air is 1 kg/m^3, the dynamic viscosity (µ) of air is 2 * 10^-5 kg/m-s, and the flow is laminar, i.e. Re = 500.
The grid-structured *CFDSOF* software is used in this simulation case.
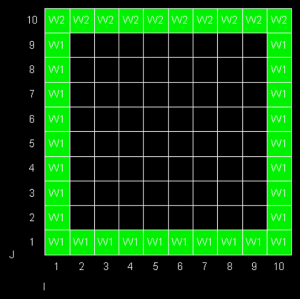
First, cavity is discritized by dividing it into cells, in this case, a 10x10 cells.
Then, after specifying the boundary condition of the walls and the iteration of the case, the iteration begins. The results of the velocity vector field and the pressure contour are shown in the images below.
It can be shown that the air is indeed moving inside the cavity and the air that is closest to the upper wall is also moving with the greatest magnitude. From the pressure contour, it can be seen that the upper-most-right corner has the greatest pressure. This is due to the fact that air is colliding at that corner and is diverted to the adjacent bottom. This collision occurs at the 4 corners of the wall, thus creating the swirling effect with the smallest velocity magnitude at the center of the swirl.
OpenFOAM Solvers
Here are solvers that OpenFOAM offers. The table below classifies the solver based on the flow of the fluid and depends on the case-by-case problem.
| No. | Solver | Algorithm | Time | Flow | Compressibility | Phase |
|---|---|---|---|---|---|---|
| 1 | simpleFoam | SIMPLE | Steady-State | Laminar/Turbulent | Incompressible | Single-phase |
| 2 | icoFoam | PISO | Transient | Laminar | Incompressible | Single-phase |
| 3 | pisoFoam | PISO | Transient | Turbulent | Incompressible | Single-phase |
| 4 | pimpleFoam | PISO+SIMPLE | Transient | Turbulent | Incompressible | Single-phase |
| 5 | interFoam | PISO+SIMPLE | Transient | Turbulent | Incompressible | Multi-phase |
| 6 | - | - | - | - | - | - |
SIMPLE = Semi-Implicit Method for Pressure Linked Equations
PISO = Pressure Implicit with Splitting of Operators
Cavity 2D with OpenFOAM
The problem we are trying to solve is lid-driven cavity. Same as previous case, the geometry is a 2 dimensional 0.1 m by 0.1 m (gamma = Lx/Ly = 1) cavity space with the upper wall moving to the positive x-axis direction at certain velocities. The boundary of right, left, and lower wall is stationary. The fluid is air with kinematic viscosity (nu) of 1 * 10-⁵ m²/s.
The INTENTION of this preliminary study is to understand the effect of Reynolds number (Re) on the air flow inside the lid-driven cavity, particularly the flow profile. At certain velocity, is it laminar, transitional, or turbulent? At what Reynolds number does the change occurs?
<math> Re = \frac{&rho U L}{&mu} = \frac{U L}{\&nu} . . . (1) </math>
where:
Re = Reynolds number (-)
rho = fluid density (kg/m³)
U = inlet velocity = upper wall velocity (m/s)
L = characteristic length = wall length = 0.1 m
mu = dynamic viscosity (kg/m-s)
nu = kinematic viscosity = 1 * 10-⁵ (m²/s)
Reynolds number can be calculated using the Eq. (1). We can vary the Reynolds number by varying the wall velocity. Here, the upper wall velocity is varied from 0.0001 m/s to 0.8 m/s with various increment. The wall velocity variation is presented at the table below.
| U (m/s) | Re (-) |
|---|---|
| 0.0001 | 1 |
| 0.01 | 100 |
| 0.02 | 200 |
| 0.03 | 300 |
| 0.04 | 400 |
| 0.05 | 500 |
| 0.1 | 1000 |
| 0.2 | 2000 |
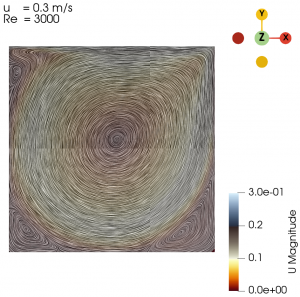
| 0.3 | 3000 |
| 0.8 | 8000 |
We used the open-source CFD software OpenFOAM for this study with simpleFoam solver for both laminar and turbulent flow, with the latter using the k-Omega turbulence model. The flow was assumed to be steady-state. A 50 by 50 hexahedral grid mesh was used in the model, where the z-axis was set to 1 cell to represent the 2 dimensional case.
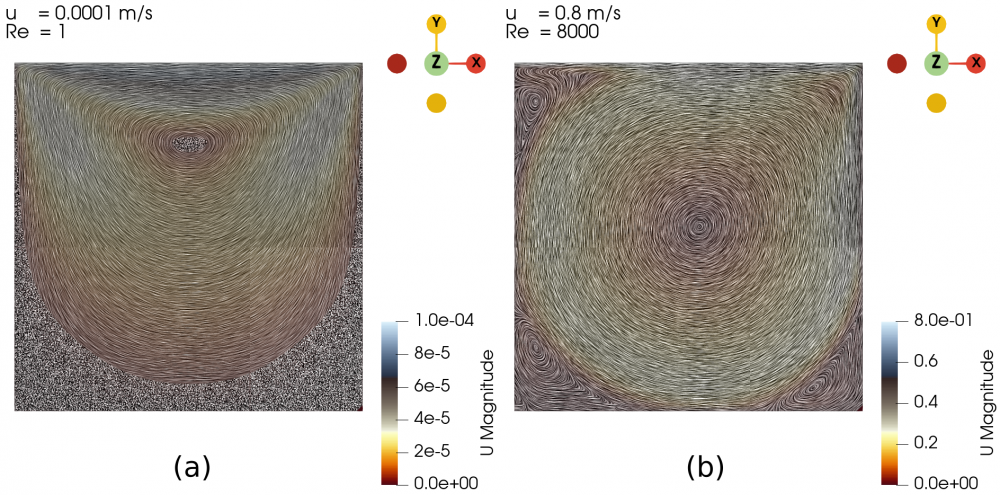
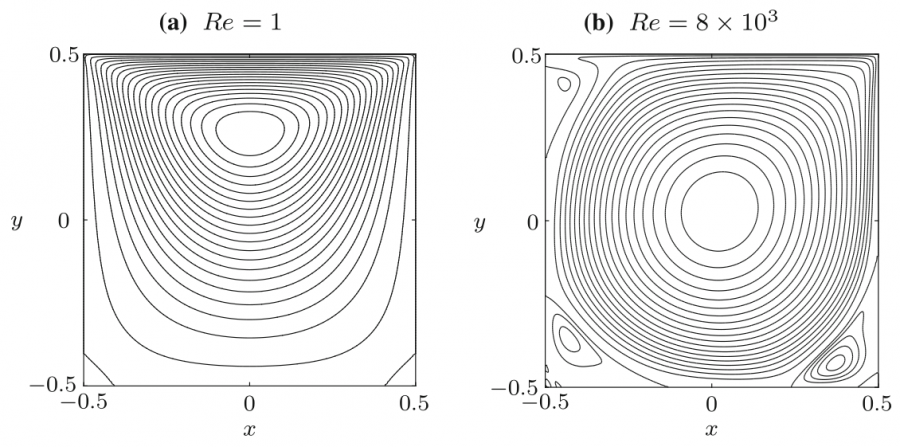
First, we validated our simulation by comparing the case with U = 0.0001 m/s and U = 0.8 m/s, hence the Re are 1 and 8000, respectively, with the case from a study conducted by Hendriketal [1], also with the same Re. The fluid flow with the isolines (streamlines) from both simulation and reference [1] can be seen in the Fig. 1 and Fig. 2 below. It can be seen that the results generated by our simulations is the same as the results obtained from [1].
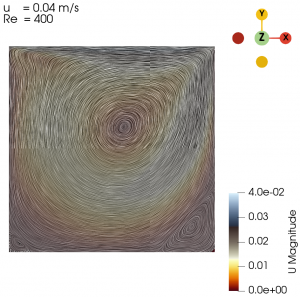
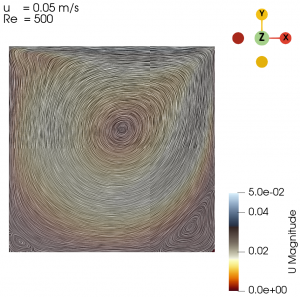
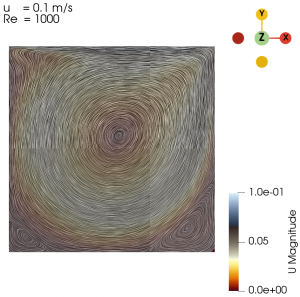
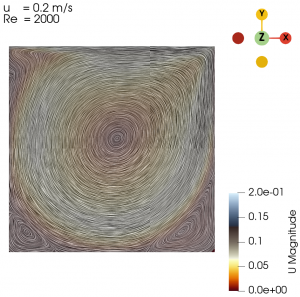
The flow with Re = 1 is laminar and almost vertically symmetrical and the flow with Re = 8000 is turbulent with 3 secondary eddies in the 3 corners of the cavity.
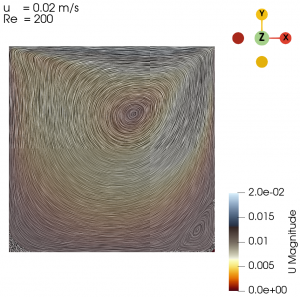
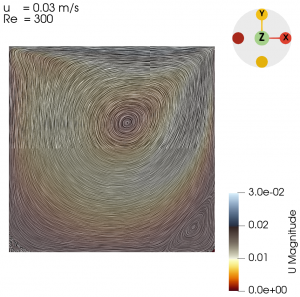
Next we varied the parameter of U from 0.01 m/s to 0.3 m/s with simpleFoam laminar model as per Table 1, and look at the flow profile of the cavity. The isolines can be seen at Fig. 3 to Fig. 10.
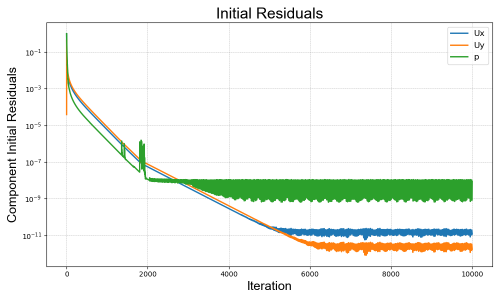
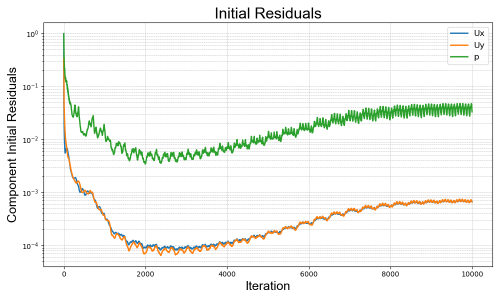
Convergence can be seen from simulation's variables residuals below.
Re = 1
Re = 8000
References:
[1] H. C. Kuhlmann and F. Romanò, "The Lid-Driven Cavity," Computational Methods in Applied Sciences, vol. 50, 2019. https://doi.org/10.1007/978-3-319-91494-7_8
Lid-Driven Cavity with DAI5 Framework
This is a video essay of the application of DAI5 Framework in understanding lid-driven cavity. The lid-driven cavity simulation is done using OpenFOAM.
Disclaimer: the video is in Bahasa Indonesia.
Lid-Driven Cavity Case File: bit.ly/CavityDAI5
Paper Draft
Grid Independency Study on the Turbulence of Lid Driven Cavity using DAI5 Framework
Mid Test with ChatGPT
| Mid Test with ChatGPT | ||
| User | ||
| ChatGPT | ||
| I am going to take an exam on the subject of basic Computational Fluid Dynamics (CFD). I need you to create a basic test consisted of 5 short-answer questions all at once and grade what I do. | ||
| Here’s a basic test on Computational Fluid Dynamics (CFD) consisting of 5 short-answer questions:
Question 1: Define the term "viscosity" and explain its significance in fluid flow. Question 2: What is the difference between laminar and turbulent flow? Provide examples of each. Question 3: Explain the concept of grid independence in CFD and why it is important for accurate simulation results. Question 4: Describe the role of the Navier-Stokes equations in CFD. What do they represent? Question 5: What are boundary conditions in CFD, and why are they crucial for setting up a simulation?
|
||
| 1. Define the term "viscosity" and explain its significance in fluid flow.
Viscosity is a measure of a fluid’s internal friction or resistance to deformation or flow when a force is applied to it. It is a fluid-specific property where fluids with higher viscosity, like syrup, deform less easily compared to fluids with lower viscosity, like water. There are two types of viscosity, the dynamic viscosity (mu) and the kinematic viscosity (nu), with units kg/m.s and m^2/s, respectively. In fluid flow applications, viscosity plays a vital role in determining whether the flow is laminar or turbulent. Viscosity is a critical property that affects fluid dynamics, influencing how fluids flow and behave under various conditions. 2. What is the difference between laminar and turbulent flow? Provide examples of each. Laminar flow is characterized by smooth, orderly motion of fluid layers, with each layer sliding past the adjacent ones with minimal to no mixing. This type of flow typically occurs at low Reynolds numbers (Re < 2000). An example of laminar flow is the flow of blood inside our capillaries or the flow of air inside a wind tunnel before contact. Turbulent flow, on the other hand, is characterized by irregular fluid motion with significant mixing and fluctuations in velocity. This type of flow typically occurs at high Reynolds numbers (Re > 4000). An example of turbulent flow is the air in and out of our respiratory system or the airflow around an airplane wing. 3. Explain the concept of grid independence in CFD and why it is important for accurate simulation results. Grid independence refers to the condition where the results of a simulation do not significantly change with further refinement of the computational grid (mesh). This can be done with a grid dependence study, which is a procedure of successive refinement of an initially coarse grid until certain key results do not change. Achieving grid independence is crucial because it ensures that the numerical solution is not influenced by the discretization of the domain, leading to more reliable and accurate results. A systematic search for grid-independent result forms an essential part of all high-quality CFD studies. 4. Describe the role of the Navier-Stokes equations in CFD. What do they represent? The Navier-Stokes equations are a set of nonlinear partial differential equations that describe the motion of fluid. They represent the conservation of momentum in fluid flow and are fundamental to the field of computational fluid dynamics. The equations account for viscosity, pressure, and external forces acting on the fluid. In CFD, solving the Navier-Stokes equations enables the prediction of velocity fields, pressure distributions, and other flow characteristics, making them essential for simulating and analyzing fluid behavior in various engineering applications. 5. What are boundary conditions in CFD, and why are they crucial for setting up a simulation? Boundary conditions in CFD define the behavior of the fluid at the boundaries of the computational domain. They specify values for variables such as velocity, pressure, and other relevant quantities at the edges of the simulation space. They ensure that the simulation reflects the physical reality of the problem being modeled, allowing for accurate predictions and are essential for producing valid and reliable CFD results. | ||
Grading:
Your explanation is clear and well-structured. You correctly define viscosity and its types (dynamic and kinematic) along with their units. You also mention its importance in fluid dynamics and how it affects flow behavior. One minor note: You could expand on how viscosity affects energy dissipation in the flow. Nonetheless, your answer is quite strong.
Excellent explanation of both laminar and turbulent flows with clear examples and correct references to Reynolds numbers. The distinction between orderly and chaotic motion is well articulated, and the examples are accurate.
Great explanation! You correctly identify grid independence and explain the grid dependence study and its importance in ensuring simulation accuracy. This is a key concept in CFD, and your description captures it thoroughly.
Your answer effectively highlights the significance of the Navier-Stokes equations in CFD. You mention their role in momentum conservation, accounting for viscosity, pressure, and forces, and how they are used to predict key flow characteristics. This is a complete and concise answer.
Good explanation of boundary conditions and their role in simulations. You correctly mention their importance in defining variables at the boundaries and ensuring physical realism in the model. A small suggestion: you could briefly touch upon specific types of boundary conditions (e.g., Dirichlet, Neumann) for more depth, but your answer is still very solid. Overall Score: 96/100 Excellent work! Your understanding of CFD fundamentals is strong, and you provided clear, well-articulated answers throughout the test. Just minor improvements in elaboration could make it even better. |
||
| How does viscosity affects energy dissipation in the fluid flow? Could you elaborate? | ||
| Viscosity affects energy dissipation in fluid flow by resisting the motion of fluid layers, converting kinetic energy into thermal energy (heat) through internal friction. Here’s how this process works in detail:
Internal Friction and Shear Stress: Viscosity causes internal friction between adjacent layers of fluid moving at different velocities. This friction leads to shear stress, which requires energy to maintain. As layers slide past each other, some of the flow’s kinetic energy is “used up” in overcoming this frictional resistance. Conversion of Kinetic Energy to Heat: The energy needed to overcome the viscous forces does not just vanish; it’s transformed into heat. This phenomenon is known as viscous dissipation. In regions with high velocity gradients (such as near solid boundaries in turbulent flows), the energy dissipation rate is higher, causing more kinetic energy to be converted to heat. Impact on Flow Types: Laminar Flow: In low-viscosity, laminar flows, this energy dissipation is relatively low, as the layers slide smoothly over each other. However, viscosity is still crucial for determining the flow regime and ensuring the orderly motion of fluid layers. Turbulent Flow: In turbulent flows, viscosity plays a larger role in dissipating energy. The chaotic, fluctuating motion of fluid particles in turbulence generates numerous small eddies, which further increase the velocity gradients and amplify the energy dissipation through viscous effects. Implications in Engineering and CFD: High-viscosity fluids dissipate more energy as heat, which can be critical for cooling and lubrication applications. In CFD, accurately modeling viscosity is essential to capture realistic energy dissipation, especially in simulations involving turbulent flows, as it affects flow stability, boundary layer characteristics, and even heat transfer predictions. Understanding viscosity's role in energy dissipation is crucial for designing efficient fluid systems, as well as for accurately predicting fluid behavior in simulations. |
||
| What are the Dirichlet and Neumann boundary conditions? What other types of boundary conditions are there? | ||
In CFD, boundary conditions define how fluid behaves at the edges of the simulation domain. Here’s a breakdown of Dirichlet and Neumann boundary conditions, along with a few other common types:
This boundary condition specifies a fixed value for a field variable (like velocity, pressure, or temperature) at the boundary. For instance, setting the temperature on a wall to a constant value (e.g., 300 K) or prescribing a fixed velocity at an inlet. Dirichlet conditions are commonly used to impose known values at inflow boundaries or solid surfaces with a constant temperature.
This condition specifies a fixed rate of change, or gradient, of a variable at the boundary rather than the variable's value itself. For example, setting the heat flux across a wall surface to a constant (which relates to the temperature gradient) or defining a zero-velocity gradient (indicating no shear stress). Neumann conditions are often applied when the exact value is unknown, but the flux or rate of change at the boundary is known, such as insulated walls (zero heat flux) or stress-free outflows.
This combines aspects of Dirichlet and Neumann conditions by defining a relationship between the variable and its gradient at the boundary. For instance, in heat transfer, it can represent convective cooling, where the heat flux is proportional to the temperature difference between the fluid and the boundary (e.g., Newton's Law of Cooling). Robin conditions are used in situations where the boundary value depends on both the internal variable and its rate of change, such as semi-permeable membranes or convective heat transfer.
This boundary condition enforces a repeating pattern in space, where the variables on one side of the boundary match those on the opposite side. For example, in simulations of flow over a regularly spaced array of objects, where the pattern of flow repeats, periodic conditions allow efficient modeling by simulating just a small section. This is especially useful in simulations of channels, waves, and symmetric or repeating systems.
This condition is applied when the domain has a plane of symmetry, where no flow or gradient exists normal to the symmetry plane. The symmetry boundary implies that the normal component of velocity and the normal gradient of scalar variables (like pressure or temperature) are zero. Useful for reducing computational load by only simulating half or a section of a symmetric geometry, like a cylindrical pipe.
Designed for flow exiting the domain, where minimal influence from the boundary on the internal flow is desired. Outflow boundaries often enforce zero gradients or “do-nothing” conditions to allow fluid to exit freely. In external flow problems, like around an airplane, far-field conditions simulate an open, infinite environment where variables gradually return to ambient values as they move away from the body. Each type of boundary condition serves a specific purpose, helping to set up simulations that accurately reflect real physical scenarios. The choice of boundary condition is crucial as it significantly affects simulation stability and results accuracy. |
||
Self-assessment Mid-Test
Rencana untuk Kelas Aplikasi CFD pasca-UTS