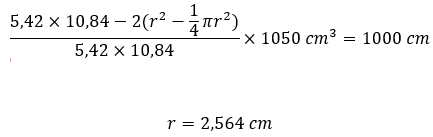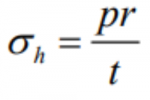Jesaya Marcel Gloryus (Metode Numerik)
Metode Numerik-02
Nama: Jesaya Marcel Gloryus
NPM: 2106727853
Contents
[hide]
Hydrogen Storage Optimization
Pressurized hydrogen storage refers to the technique of storing hydrogen gas under high pressure in order to increase its density and store it in a compact manner. Hydrogen, being a low-density gas, requires compression to achieve practical storage volumes.
The most common method of pressurized hydrogen storage is through the use of high-pressure tanks, often referred to as hydrogen cylinders. These cylinders are typically made of materials like carbon fiber composite or steel that can withstand the high pressure. The hydrogen gas is compressed into the cylinder, and a valve system allows for controlled release or extraction of the gas when needed.
Here is the steps to optimize hydrogen storage:
1. Define the Objectives: Clearly define your optimization goals and requirements. Consider factors such as energy density, safety, cost, scalability, refueling/recharging time, and specific application needs. Identifying your objectives will help guide your optimization efforts.
2. Assess Current Storage Methods: Evaluate the existing hydrogen storage methods available and assess their strengths and limitations. This includes compressed gas storage, liquid hydrogen storage, metal hydrides, carbon-based materials, chemical hydrides, and hydrogen carriers. Understand the characteristics and performance of each method.
3. Research and Development: Stay updated with the latest research and development in hydrogen storage technologies. Explore academic publications, scientific research papers, and industry reports to understand emerging trends, new materials, and innovative approaches to hydrogen storage. Collaborate with experts and researchers in the field to leverage their knowledge and insights.
4. Material Development: Investigate and develop new materials or modify existing ones to enhance hydrogen storage performance. This may involve exploring advanced metal hydrides, carbon-based materials with high adsorption capacity, or novel storage media. Aim to improve storage capacities, kinetics, stability, and reversibility of the materials.
5. System Integration: Consider the entire hydrogen storage system, including hydrogen production, storage, and utilization. Optimize the integration of various components to improve overall efficiency. Explore synergies with renewable energy sources, such as coupling hydrogen storage with electrolysis powered by solar or wind energy, to enhance sustainability.
6. Safety and Regulations: Ensure that safety aspects are thoroughly addressed in the optimization process. Consider safety measures for high-pressure storage, cryogenic systems, and chemical compounds. Adhere to relevant regulations and standards to guarantee safe handling, storage, and transportation of hydrogen.
7. Modeling and Simulation: Utilize computer modeling and simulation tools to assess and optimize storage system designs. Simulate the behavior of different storage methods under various operating conditions and evaluate their performance. This allows for iterative improvements and cost-effective analysis before implementing physical prototypes.
8. Cost Analysis: Conduct a detailed cost analysis of different storage methods and their associated infrastructure. Consider factors such as capital costs, operational expenses, maintenance, and potential life-cycle costs. Identify opportunities for cost reduction, such as improved manufacturing processes, material selection, or scalability.
9. Prototyping and Testing: Build prototypes based on optimized designs and evaluate their performance through rigorous testing. Assess parameters such as storage capacity, efficiency, durability, safety, and reliability. Iterate and refine the design based on testing results to further optimize the storage system.
10. Scale-Up and Commercialization: Once you have a well-optimized hydrogen storage system, focus on scaling up production and commercialization. Collaborate with industry partners, investors, and regulatory bodies to facilitate the deployment and adoption of your optimized storage technology.
There are a number of factors that can be optimized to improve the efficiency of hydrogen storage. These include:
- The material used for storage: The material used for hydrogen storage has a significant impact on the storage capacity and efficiency. For example, metal hydrides have higher hydrogen storage capacities than carbon nanotubes, but they are also more expensive.
- The storage conditions: The storage conditions, such as temperature and pressure, can also have a significant impact on the storage efficiency. For example, hydrogen can be stored more efficiently at cryogenic temperatures than at room temperature.
- The design of the storage system: The design of the storage system can also have a significant impact on the storage efficiency. For example, a well-designed storage system can minimize the amount of energy required to store and release hydrogen.
Tugas Case Study Hydrogen Storage Optimization
Objectives : 1 Liter Pressurized Hydrogen (8 bar) storage
Constraint : Budget maximum Rp500.000
Design Variable : Geometry, Material Selection, Material Thickness
Calculation
Geometrical Constraint
Geometry Optimization's goal is to minimize the surface area of hydrogen storage in order to save material needs. The geometry could have many combinations of radius and height in order to achieve 1 liter size. Below are programming code to calculate the minimum surface area to achieve 1 liter volume
import numpy as np
from scipy.optimize import minimize
# Define the objective function
def objective(x):
radius, height = x
surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
# Define the volume constraint function
def volume_constraint(x):
radius, height = x
volume = np.pi * radius**2 * height
return volume - 1000
# Define the optimization problem
x0 = [1.0, 10.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': volume_constraint}
problem = minimize(objective, x0, bounds=bounds, constraints=constraint)
# Extract the optimized results
optimized_radius = problem.x[0]
optimized_height = problem.x[1]
minimum_surface_area = problem.fun
# Print the optimized results
print("Optimal Geometry:")
print("Optimal Radius: cm", optimized_radius)
print("Optimal Height: cm", optimized_height)
print("Minimum Surface Area: cm", minimum_surface_area)
Berikut merupakan hasil perhitungan
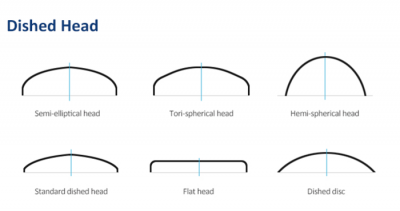
End Cap Geometry
To minimize stress concentration at the corners of geometry, the torispherical end heads is a good alternatif. Torispherical heads are designed to withstand high internal or external pressures. The curved shape of the head helps distribute the pressure more evenly, reducing stress concentrations compared to flat or hemispherical heads. This design provides structural integrity and enhances the overall strength of the pressure vessel or tank. Torispherical heads offer good volume efficiency, meaning they provide a higher storage capacity within a given diameter compared to other head designs. The curved shape allows for a larger internal volume while maintaining a compact form factor. This can be particularly advantageous when space is limited, as it allows for more efficient use of available storage area.
However, the formation of these end caps certainly reduces the volume of the hydrogen tank. Therefore, the basic geometry of the tank is made with a larger volume as above, namely 1050 cm^3 so that the absorption volume due to these end caps does not fall below the 1 liter limit that has been set. The area is proportional to the volume so that comparison calculations can be carried out. Through this calculation, the radius of the fillet can be found.
The fillet radius obtained for the tank's end caps is 2,564 cm
Material Strength Constraint
In a pressurized storage system, the strength of the material and the plate thickness of the tank must be able to withstand the pressure of the gas pressing in all directions on the tank wall. In terms of specifications, this 1 liter hydrogen tank also has a pressure limit of 8 bar. The thickness of this tank plate can be calculated by the following hoop stress equation.
The size range of plate thickness should not be less than 1/5 of the tank radius. According to ASME BPV Code Section VIII D.1, the minimum tank plate thickness is 1/16 in or 1.59 mm without considering corrosion, material or dimensions.