Vynna Alviolina Indriyana
Contents
INTRODUCTION
Hi everyone! My name's Vynna, I'm a student in Numerical Method 1 Class. My student Number is 2106634036. Here, I'll upload my progress in the class. Hopefully through this page, I can increase my conscious learning and spread knowledges to readers.
CLASS SUMMARY
This content will be updated weekly after discussion meeting with Mr. Ahmad Indra Siswantara in class.
Numerical Method Use in Mechanical Engineering (22/5/2023)
In the class, we've been introduced to the concept of "I am my consciousness". We fully control our consciousness to think, learn, and act. It what makes us different from Artificial Intelligence. They may able to store large number of data, but we have consciousness that can utilize that data to solve real life problems. We've also been introduced to CCIT (Cara Cepat Ingat Tuhan). Nothing perfect in this world, except the Lord Allah SWT Himself. Our knowledge is just a speck of dust in this world, therefore we need to keep learning.
After that we start our discussion regarding numerical method use in mechanical engineering. I state my opinion : "I've been told by my lecturer in CAD/CAM class that we need numerical method as an approach of machine works. For example, the milling machine is programmed to machining at some exact points. But in the reality, no computer able to reach specific points. It uses numerical method approach to the point with error the tolerance number that has been set by operator."
Other students also stated their opinion and it can be sum up to these :
1. Program manufacture machines
2. Solve problems with lot of variables
3. Calculate real system simulation
4. Solve complex system that hardly solved by analytic method
5. Formulate mathematical model of system
CLASS ASSIGNMENT
All assignments here can be done with deep researching and help from Artificial Intelligence that elaborated with conscious thinking. References will be linked at the end of the quotes.
Design and Optimization of Compressed Hydrogen Storage
Compressed Hydrogen Storage
Compressed hydrogen storage is a method of storing hydrogen gas at high pressures to achieve a higher energy density and facilitate its use as a fuel. Hydrogen is an extremely lightweight gas and has a low energy density compared to liquid fuels, making it challenging to store and transport in large quantities. Compressing hydrogen gas increases its density and allows for more hydrogen to be stored within a given volume.
The process of compressed hydrogen storage involves using a high-pressure container, typically made of strong materials such as carbon fiber composites or metal alloys, to hold the hydrogen gas. The gas is compressed to pressures ranging from 3,000 to 10,000 pounds per square inch (psi), or even higher in some cases. These high pressures significantly increase the amount of hydrogen that can be stored within a given volume.
The compressed hydrogen storage system typically includes valves, pressure regulators, and safety devices to ensure safe handling and release of the stored hydrogen. When the compressed hydrogen is needed, it can be released from the storage container and used as a fuel for various applications, such as fuel cell vehicles or industrial processes.
One advantage of compressed hydrogen storage is that it allows for quick refueling or recharging, similar to refueling a conventional gasoline or diesel vehicle. However, it does require robust storage containers and can be associated with safety concerns due to the high pressures involved. It is essential to handle compressed hydrogen with caution to prevent leaks or ruptures.
It's worth noting that there are other methods of hydrogen storage, such as cryogenic liquid storage and solid-state storage, each with its own advantages and challenges. The choice of storage method depends on factors such as the intended application, infrastructure availability, safety considerations, and cost-effectiveness.
Specification Requirements
Required specifications of the case are 1 liter hydrogen capacity with 8 bar pressure and maximum cost 500,000 IDR
Optimized Design
Designing a compressed hydrogen storage system with specific cost constraints requires careful consideration of various factors. Here's a conceptual design for a 1-liter hydrogen storage system with an 8-bar pressure rating and a maximum cost of 500,000 IDR:
Storage Container:
Material: Carbon fiber composite
Volume: 1 liter
Pressure Rating: 8 bar (800 kPa)
Cost: Approximately 300,000 IDR (costs may vary)
Valves and Pressure Regulator:
High-pressure valve: To control the flow of hydrogen into and out of the storage container.
Pressure regulator: To regulate the hydrogen pressure to a safe and consistent level for usage.
Cost: Approximately 100,000 IDR (costs may vary)
Safety Devices:
Pressure relief valve: To prevent over-pressurization and ensure safety. Burst disc: A safety device that releases excess pressure in case of an emergency. Cost: Approximately 50,000 IDR (costs may vary) Piping and Connectors:
Stainless steel or high-pressure-rated tubing and connectors to ensure reliable hydrogen flow between components. Cost: Approximately 50,000 IDR (costs may vary) Installation and Labor:
Labor costs for assembling and installing the system. Cost: Approximately 100,000 IDR (costs may vary) Please note that the cost estimates provided are approximate and can vary depending on factors such as location, availability of materials, and labor costs. It's essential to consult with hydrogen storage system manufacturers or suppliers to obtain accurate cost estimates for your specific requirements.
Additionally, it's important to adhere to safety regulations and guidelines when designing, installing, and operating a compressed hydrogen storage system. Proper training and knowledge about hydrogen safety practices are crucial to ensure safe handling and operation of the system.
Optimised Hydrogen Storage
GEOMETRICAL COMPENSATION
Base Geometry
One of the main components of designing the pressurized hydrogen storage is the measurements and geometry of the storage. Through our discussions in class and individual case studies, students in our class collectively agreed that the ideal shape of the storage is a cylindrical shape akin to those generally utilized by the industry. The parameters of the cylindrical shape however still needs to be found out using the methods that we have learned over the entire course of Numerical Method class.
The goals of the optimization process of this hydrogen storage as mentioned above in the case study section is to create a pressurized hydrogen storage that fulfills the requirements while remaining cost-effective. One of the main contributors to cost of production is the amount of material being used, which in the case of a cylindrical container, equal to the surface area of the product. The lower the total surface area of the product, the lower the total effective material that is required to craft it. For our case, the surface area needs to be minimized while maintaining a constraint of volume being equal to 1 liter or 1000 cubic centimeters. The radius and height of a cylinder that fulfills both qualities can be obtained using a simple optimization function that can be numerically computed using suitable code made in Python or MATLAB. For the purpose of this project, I utilized Python to create a code that manually computes the radius and height of a cylinder of 1000 centimeter cubic volume. There are other libraries such as SciPy that has compiled code for optimization into a singular function, but for the purpose of learning the following code is done manually.
Objective: Minimize surface area of cylindrical structure
Constraint: Internal volume of cylindrical structure must be equal to 1000 cubic centimeters (1 liter)
The first section of the code is to obtain a general range of radius values where the surface area is minimum, shown below:
from math import pi
import pprint
'''
r = radius
circle_area = pi * r**2
circle_circumference = 2 * pi * r
h = height
cylinder_volume = pi * r**2 * h
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * h)
constraint for cylinder_volume be a constant of 1 liter (cubic centimeter)
cylinder_volume = 1000
h in terms of r
h = 1000/(pi * r**2)
substitute in
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
'''
mylist = [] # create a list of (surface area, radius)
for r in range(1, 21): # assume a maximum of 20cm radius
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
mylist.append((cylinder_surface, r))
# test
pprint.pprint(mylist)The code above displays iterations from radius of 1 cm to 20 cm and their corresponding surface area values. By inspection, we can see that the minimum surface area occurs in the region between radius of 5 and 6 cm. For precision, we continue the code with a looping function to obtain the precise point where the minimum surface area occurs, and continue with computing the height for verification.
# once we find the range where area is minimum
# we can increment in smaller steps for precision
r = 5
surface_list = []
while True:
cylinder_surface = 2 * (pi * r**2) + (2 * pi * r * 1000/(pi * r**2))
surface_list.append((cylinder_surface, r))
r += 0.01
if r > 6:
break
print('minimum surface area and radius: ', min(surface_list))
min_surface = min(surface_list)[0]
sf = "Minimum surface of a 1000ml tank = {:0.2f} square centimeters"
print(sf.format(min_surface))
radius = min(surface_list)[1]
print("Radius of 1000ml tank = {:0.2f} centimeters".format(radius))
height = 1000/(pi * radius**2)
print("Height of 1000ml tank = {:0.2f} centimeters".format(height))
sf = "Ratio of height to radius of a minimized surface can = {:0.2f}"
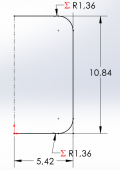
print(sf.format(height/radius))The result obtained by the code is shown on the right, where the suggested geometry for a cylindrical tank for 1 liter volume should maintain a 2:1 height to radius ratio with the radius being 5.42 cm, and the height at 10.84 cm consequently.
End Cap Compensation
Using a purely cylindrical geometry for the storage tank is likely to be dangerous due to the existence of the corners on the ends, which present stress concentration regions or sites of failure. Most pressure vessels take on a curved shape on their ends to reduce stress concentration by using three geometries: hemispherical, ellipsoidal, and torispherical. Highest volume and surface area addition to lowest addition also goes in the same order. Therefore, since our goal is to minimize surface area while maintaining the same volume, it is most efficient to take on a torispherical end cap shape. The torispherical shape can be simplified as the cylindrical shape that has been given partial filleting. This filleting adjustment will reduce the overall volume of the structure, however. Therefore we need to adjust the geometrical parameters to compensate for the reduction from the filleting to create the end cap.
We can set a fillet of radius equal to half the radius of the container to create a smooth curvature for greater stress concentration reduction. An example sketch has been made via a computer-aided design program to visualize the reduction in cross-sectional area from the circumferential face. By law of proportionality, a percentage reduction in the cross sectional area would be equal to the same reduction in volume, therefore we can calculate the percentage reduction and apply inversely to our required volume to obtained the new increased volume constraint.
As shown, assuming a fillet radius of half the container radius, we have a new volume constraint of 1056.69 cubic centimeters to account for the percentage reduction in volume following formation of torispherical end caps through filleting. We can repeat the iteration process that was previously used to obtain new radius and height values for the cylinder. Upon iterating the first section of code, we find that the minimum surface area occurs between values of 5 and 6 cm radii again, therefore the upper and lower bounds of the second set of code do not need to be adjusted. The final results as as follows:
minimum surface area and radius: (574.3098652360588, 5.519999999999989)
Minimum surface of a 1056.69ml tank = 574.31 square centimeters
Radius of 1056.69ml tank = 5.52 centimeters
Height of 1056.69ml tank = 10.45 centimeters
Ratio of height to radius of a minimized surface can = 1.89LITERARY PARAMETERS
The range of wall thickness that is applicable is also not arbitrary outside of remaining less than one-fifth of the vessel radius. ASME BPV Code Section VIII D.1 states that wall thickness should always be at least 1/16 in (1.59 mm), not considering corrosion allowance, material, or dimensions. Literary source "Analysis, Synthesis, and Design of Chemical Processes" gives heuristics for wall thickness for rigidity based on vessel diameter: 4 mm (0.25 in) for 1.07 m (42 in) diameter and less than 8.1mm (0.32 in) for 1.07-1.52 m (42-60 in) diameter, and 11.7 mm (0.38 mm) for more than 1.52 m (60 in) diameter (Turton et al., 2012). Taking a conservative approach of setting the minimum thickness to be in between 1.59mm and 4mm, thereby 2.8mm, we will begin the iteration of the thickness from 2.80mm up to 11.04mm at increments of 0.01mm for precision.
Based on data obtained from Ferrobend, a typical workpiece of AISI 316 stainless steel has the mechanical properties as shown. For the purpose of our testing, we will utilize both a conservative and less conservative method by setting our limit at the yield strength as well as the maximum tensile strength to signify failure.
We can use a simple code to numerically iterate the possible thickness and hoop stress values:
r = 5.52e-2
p = 800000
t = 2.8e-3
while t < 11e-3:
hoop = (r * p)/(t)
print('for thickness', t, 'hoop stress =', hoop, "Pa")
t += 0.1e-3
if hoop > 205e9:
breakFrom the above code we obtain hoop stress values for each iterated thickness values from 2.8 mm to 11 mm. A further constraint was placed in the final lines where the looping would stop if the total hoop stress exceeded the yield strength of the material (stainless steel AISI 316).
Cost Constraints
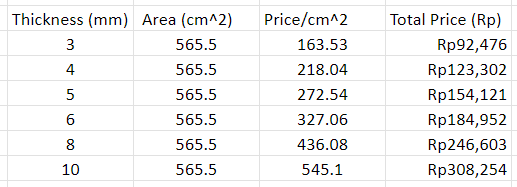
With the geometrical parameters available, we need to compare with the cost constraint that was provided which is that the total cost for materials used should not exceed Rp300.000,-. Therefore, from the material that has been previously considered, we must select the thickness which remain within the cost range. As this is a small-size thin-walled vessel, the most likely method of manufacture is through sheet-metal manufacturing like those used to manufacture storage and beverage cans. Therefore, material purchase would be done in the sheet-metal or plate form. The design used for creating 1L Storage is using 10 cm diameters tube with 13cm length. Therefore we can find the surface area is 565.5 cm^2. Therefore we can calculate the thickness using pricelist of 316 plates from distributor PT Citra Anggun Lestari.
With the limited cost of Rp300.000, the right thickness that meet parameters is the 8 mm thickness. Hence we can still have budget for the valve and pressure regulators.
Even with the thickest tube, it still hasn't exceed budget limit. Hence we can convert that budget to increase ergonomic side of the hydrogen tank.