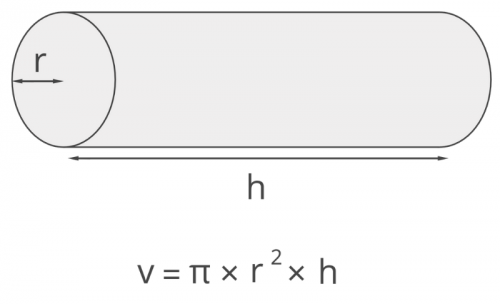Galih Hendra Bhagaskara

Hydrogen Storage

Designing and optimizing a 1-liter pressured hydrogen storage system requires consideration of several factors including safety, efficiency, and storage capacity . By addressing these key factors, the design can ensure safe operation, maximize the storage capacity within the given volume, and optimize the system's efficiency. Here are some key points to consider:

1. Material Selection

The storage vessel should be made of materials capable of withstanding high-pressure hydrogen storage. The chosen material should have a high strength-to-weight ratio to minimize weight while maintaining safety, Common options include carbon fiber reinforced composite materials or high-strength steel.

2. Vessel Design

The vessel design should consider factors like internal pressure, safety factors, and weight constraints. The shape and configuration of the vessel should distribute stress uniformly, while the wall thickness needs to be optimized for strength and weight requirements. Welding and joint design should ensure structural integrity. Pressure relief mechanisms, such as valves and burst discs, are essential for safety. Proper design considerations can prevent issues like stress concentrations, fatigue cracks, or material degradation over time.

3. Safety Features

Incorporate safety features to ensure reliable and secure hydrogen storage. This may include pressure relief valves, burst disks, and other pressure control mechanisms to prevent over-pressurization. Safety considerations are crucial due to hydrogen's flammability and the potential hazards associated with high-pressure storage.

4. Efficiency and Capacity

Efficiency and capacity are key considerations in designing a 1-liter pressured hydrogen storage system. Maximizing storage capacity involves utilizing advanced adsorption materials and minimizing dead volume. Efficiency is enhanced through materials with low hydrogen permeation, reliable sealing mechanisms, and optimized fill/discharge rates. Energy efficiency can be improved by optimizing insulation and integrating with other system components

5. Testing & Validation

Performance testing evaluates its functionality and ability to store and release hydrogen safely. Burst pressure and pressure cycling tests determine the vessel's structural integrity and durability. Prototyping and field testing provide real-world data for improvements. Thorough testing is essential to identify flaws and meet safety requirements. Collaboration with experts and specialized facilities is recommended for accurate and reliable testing.

Design and Optimization 1 Liter Pressured Hydrogen Storage

Material

Material yang digunakan pada pembuatan hydrogen tank disini yaitu sheet metal ASTM A36 dengan yield strength 248 MPa / 36.000 psi. Lalu kita dapat menghitung allowable stress value = 2/3 x Yield Strength = 165, 3 MPa / 24.000 psi.

Dimension Tank

So that production costs are not too high, a suitable form of hydrogen storage tank is a cylinder with curved ends. If we build a cylinder with an approximate diameter of 12 cm with an internal volume of about 1 liter (1000 cm^3), the height of the tank will be approx.

h = 1000 / (pi x r x r) = 1000 / (3.14 x 6 x 6) = 1000 / 113,04 = 8,85 cm. So the dimensions of the storage tank would have a diameter of 12 cm with a height of around 8,85 cm

To calculate the required wall thickness of the storage vessel in millimeters (mm), we can use the Barlow's formula, assuming a single-welded butt joint and a material with an allowable stress (S) of 24,000 psi and a modulus of elasticity (E) of 0.60.

Given parameters:

Pressure (P) = 8 bar = 116 psi

Radius (R) = 50 mm

Allowable stress (S) = 24,000 psi

Corrosion allowance = 1 mm

First, convert the corrosion allowance from mm to inches:

Corrosion allowance = 1 mm / 25.4 = 0.0394 inches

Dimensi Tabung

import math

def calculate_surface_area(radius, height):
    lateral_area = 2 * math.pi * radius * height
    base_area = math.pi * radius**2
    return 2 * base_area + lateral_area

def find_optimal_dimensions(volume):
    min_surface_area = float('inf')
    optimal_radius = 0
    optimal_height = 0

    for radius in range(1, int(volume**(1/3)) + 1):
        height = volume / (math.pi * radius**2)
        surface_area = calculate_surface_area(radius, height)

        if surface_area < min_surface_area:
            min_surface_area = surface_area
            optimal_radius = radius
            optimal_height = height

    return optimal_radius, optimal_height

volume = 1000
radius, height = find_optimal_dimensions(volume)
print(f"Optimal dimensions for a tube with a volume of {volume} cm³:")
print(f"Radius: {radius} cm")
print(f"Height: {height} cm")

Next, calculate the required wall thickness (t) using the Barlow's formula:

 t = (P * R) / (2 * S + P * E - 1.2 * P)

 = (116 psi * 50 mm) / (2 * 24,000 psi + 116 psi * 0.60 - 1.2 * 116 psi)

 ≈ 2.007 mm

Therefore, based on the given parameters and assuming a single-welded butt joint and a material with an allowable stress (S) of 24,000 psi and a modulus of elasticity (E) of 0.60, the required wall thickness of the storage vessel is approximately 2.007 mm.

Surface Area

import math

 Height = 8,85
 Diameter = 12
 thickness = 2.007

def calculate_surface_area(height, diameter, thickness):
    height_mm = height
    diameter_mm = diameter
    thickness_mm = thickness
    
    radius_inner = (diameter_mm / 2) - thickness_mm
    radius_outer = diameter_mm / 2
    
    area_inner = 2 * math.pi * radius_inner * height_mm
    area_outer = 2 * math.pi * radius_outer * height_mm
    area_top_bottom = math.pi * (radius_outer**2 - radius_inner**2)
    
    total_surface_area = area_inner + area_outer + area_top_bottom
    
    return total_surface_area

surface_area = calculate_surface_area(height, diameter, thickness)

print(f"The surface area of the cylindrical vessel is approximately {surface_area:.2f} square millimeters.")

Dari hasil codingan diatas didapatkan surface area optimal dari tabung hidrogen:

Luas Area : 618.68 cm^2