Imam Akbar Bastary
Introduction
Nama : Imam Akbar Bastary
NPM : 2106640695
Kelas : Metode Numerik 01
Progress Tugas Minggu ke-1
Pada minggu pertama ini kita mahasiswa kelas Metode Numerik-01 diberikan study case mengenai sesuatu yang harus diperhatikan dalam mendesain dan mengoptimalkan tangki hidrogen yang berkapasitas 1 liter serta mempunyai tekanan 8 bar dengan biaya produksi tidak lebih dari Rp. 500.000. berikut adalah beberapa hal yang perlu diperhatikan:
Bahan Tangki
Pilih bahan yang kuat dan tahan terhadap tekanan dan korosi yang disebabkan oleh hidrogen. Pilihan bahan yang umum digunakan termasuk serat karbon, baja tahan karat, atau aluminium. Pastikan bahan yang dipilih sesuai dengan anggaran biaya produksi.
Ketahanan Terhadap Tekanan
Pastikan tangki memiliki ketahanan yang cukup terhadap tekanan 8 bar. Desain dan bahan tangki harus mampu menahan tekanan tersebut dengan aman dan tidak terjadi kebocoran.
Keamanan
Pastikan tangki memiliki sistem keamanan yang memadai, seperti katup pengaman tekanan dan relief valve. Sistem ini akan membantu mengurangi risiko kegagalan struktural dan mencegah peningkatan tekanan yang berlebihan.
Volume dan Dimensi
Sesuaikan volume tangki dengan kebutuhan Anda, yaitu 1 liter. Pertimbangkan dimensi tangki untuk memastikan tangki dapat diintegrasikan dengan perangkat lainnya dan memenuhi spesifikasi ruang yang tersedia.
Biaya Produksi
Tetapkan batasan biaya produksi maksimum sebesar Rp. 500.000 dan perhatikan biaya bahan, biaya produksi, serta biaya desain dan pengujian. Optimalkan desain dan material tangki untuk mencapai biaya produksi yang sesuai dengan anggaran.
Uji dan Sertifikasi
Pastikan tangki melalui pengujian yang sesuai dan memenuhi standar keamanan dan kualitas yang berlaku. Uji tekanan dan uji kebocoran diperlukan untuk memastikan keamanan dan performa tangki.
Efisiensi Ruang
Perhatikan efisiensi ruang dalam mendesain tangki. Desain yang kompak akan memungkinkan pemanfaatan ruang yang optimal dan memungkinkan integrasi dengan perangkat lainnya.
Penggunaan Energi
Perhatikan efisiensi energi dalam produksi dan penggunaan tangki hidrogen. Optimalkan desain untuk mengurangi konsumsi energi selama proses produksi dan penggunaan tangki.
Skala Produksi
Pertimbangkan skala produksi tangki hidrogen. Pada skala produksi yang lebih besar, biaya produksi per unit biasanya lebih rendah. Namun, pastikan untuk tetap memenuhi anggaran biaya produksi maksimum yang ditetapkan.
Regulasi dan Standar
Pastikan tangki mematuhi semua regulasi dan standar yang berlaku untuk keselamatan dan kualitas. Pastikan juga untuk memperhitungkan biaya sertifikasi jika diperlukan.
Kode Phyton
Dibawah ini disajikan kode Python yang dapat digunakan untuk mengoptimalkan penyimpanan hidrogen pada tekanan 8 bar dengan kapasitas 1 liter dan anggaran maksimal Rp500.000:
from scipy.optimize import minimize
# Harga dan kapasitas yang dibutuhkan
harga_per_unit = 500000 # Rupiah
kapasitas_per_unit = 1 # Liter
# Anggaran maksimal
anggaran_maksimal = 500000
# Fungsi Akhir
def fungsi_akhir(x):
return -x * kapasitas_per_unit
# Kendala yang terjadi
def kendala(anggaran):
return anggaran_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_akhir, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Biaya Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit yang bisa dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan yang didapat:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total anggaran:", solusi.x[0] * harga_per_unit, "Rupiah")
Output:
Status: Biaya Optimal
Jumlah unit yang bisa dibeli: 1
Total kapasitas penyimpanan yang didapat: 1.0 liter
Total anggaran: 500000.0 RupiahDalam kode di atas, tujuan utama adalah memaksimalkan jumlah unit penyimpanan hidrogen yang akan dibeli. Batasan anggaran diimplementasikan menggunakan fungsi kendala untuk memastikan bahwa total biaya tidak melebihi anggaran maksimal yang telah ditentukan. Output dari kode ini akan menampilkan jumlah unit yang perlu dibeli, total kapasitas penyimpanan, dan total biaya yang diperlukan.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 500000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(x):
return budget_maksimal - (harga_per_unit * x[0])
kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]
# Nilai awal
x0 = [0]
# Batasan
batas = [(0, None)]
# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)
# Menampilkan hasil
tampilkan_hasil(solusi)
# Menghasilkan grafik
anggaran = np.linspace(0, 10, 100) # Range anggaran
kapasitas = anggaran * kapasitas_per_unit # Total kapasitas penyimpanan untuk setiap anggaran
biaya = anggaran * harga_per_unit # Total biaya untuk setiap anggaran
plt.figure()
plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan')
plt.plot(anggaran, biaya, label='Total Biaya')
plt.axhline(solusi.x[0] * kapasitas_per_unit, color='r', linestyle='--', label='Jumlah Unit Optimal')
plt.axvline(solusi.x[0], color='g', linestyle='--', label='Anggaran Optimal')
plt.xlabel('Anggaran')
plt.ylabel('Kapasitas/Biaya')
plt.title('Optimisasi Penyimpanan Hidrogen')
plt.legend()
plt.grid(True)
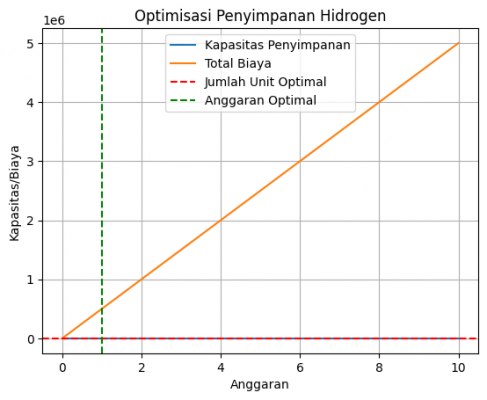
plt.show()Dalam kode di atas, terdapat perhitungan untuk menentukan jumlah unit optimal yang harus dibeli berdasarkan harga per unit, kapasitas per unit, dan anggaran maksimal yang diberikan. Kode ini mencari solusi terbaik yang menghasilkan total kapasitas tertinggi tetapi tetap berada dalam batas anggaran yang ditentukan. Hasilnya kemudian dicetak, termasuk jumlah unit, kapasitas total, dan biaya total yang dibutuhkan. Selain itu, kode ini juga menghasilkan grafik yang menunjukkan hubungan antara kapasitas dan anggaran dalam optimisasi penyimpanan hidrogen.
Apabila kode dijalankan, akan diperoleh output berupa jumlah unit yang optimal, total kapasitas penyimpanan, dan total biaya yang dibutuhkan. Selain itu, akan ditampilkan juga grafik yang memperlihatkan hubungan antara kapasitas dan anggaran dalam konteks optimisasi penyimpanan hidrogen. Grafik tersebut membantu memvisualisasikan bagaimana hubungan antara kapasitas dan anggaran mempengaruhi solusi optimal yang ditemukan.