Ethanael Hanusa
Biodata Diri
Nama :Ethanael Hanusa Tempat,Tanggal Lahir:Jakarta,24 oktober 2000
Saya merupakan seorang mahasiswa FTUI angkatan 2018 jurusan Teknik Mesin. Saya merupakan salah satu ciptaan terbaik Tuhan yang Maha Esa, karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk.
Contents
Metode Numerik
Selama mengikuti perkuliahan di jurusan teknik mesin, saya telah mempelajari mata kuliah metode numerik selama 1/2 semester. Selama 1/2 semester saya telah mempelajari banyak hal seperti, metode Newton Raphson, metode seccant, metode bisection, interpolasi, regresi liner, dan lain-lain. Setelah mempelajari hal tersebut saya merasa metode numerik berguna dalam kehidupan saya sehari-hari, dimana saat saya melakukan percobaan di lab, akan memperoleh data, data tersebut dapat diolah menggunakan regresi linear agar mendapatkan jawaban yang dicari.
Tujuan Metode Numerik:
- 1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik. Contoh:Persamaan Alajabar, algoritma, dan lain-lain
- 2. Mengerti aplikasi metode numerik
- 3. Mampu menerapkan metode numerik dalam persoalan teknik
- 4. Mendapat nilai tambah /adab sehingga kita menjadi orang yang lebih beradab
Sebelum UTS saya sudah emmeplajari banyak hal seperti: Metode Newton raphson, metode seccat, regresi linear, interpolasi, dan lain-lian, dan belajar menggunakan excel untuk menyelesaikan persamaan-persamaan tersebut
Pertemuan 11 November 2020
Pada pertemuan hari Rabu, 11 November 2020 saya mempelajari bahwa walaupun dengan menggunakan komputer yang katanya "pintar" tidak selalu dapat memcahkan semua masalah karena memiliki limit ,dan sebenarnya bodoh. Kitalah sebagai user dari komputer tersebut yang pintar dan dapat memperoleh pemecahan masalah tersebut. Namun tidak semua masalah dapt dipecahkan oleh manusia karena banyak ketidaktahuan manusia. Ketidaktahuan manusia inilah yang harus membuat kita sebagai manusia tidak sombong. karena pada sejatinya hanyalah Tuhan yang Maha Esa yang mengetahui semua hal.
Openmodelica
Saya belajar mengenai openmodelica secara online dan akan saya share apa yang sudah saya pelajari
Pertemuan Rabu 18 November 2020
Pada hari rabu 18 November 2020 saya mengikuti kelas metode numerik pukul 16.00 Pada hari ini saya belajar mengenai openmodelica dari teman-teman sekelas saya dengan berbagai macam kasus yang ada. Setelah saya belajar mengenai specialization model pada openmodelica pada sebelumnya, pada hari ini saya mempelajari mengenai openmodelica dengan specialization class dan function, saya membuat fungsi sebuah kelas dan membuat fungsi yang dapat memanggil fungsi kelas tersebut
Openmodelica
Saya belajar mengenai fungsi panggil dan dapat menyelesaikan persamaan menggunakan metode gauss di openmodelica
Pertemuan Rabu, 25 November 2020
Pada pertemuan hari rabu.25 november 2020 ada diskusi mengenai openmeodelica yang dijelaskan oleh teman kami, josiah enrico. josiah membuat openmodelica untuk menjelaskan mengenai fungsi array, menggunakan pembuatan metode newton raphson. Untuk fungsi array sendiri diperlukan karena ada banyak masalah yang tidak selesai berupa satu solusi namun berupa himpunan penyelesaian. Selanjutnya saya mempelajari bagaimana cara membuat openmodelica untuk gauss jordan dengan membuat fungsi sendiri. Saudara christo mengajarkan kami di kelas bagaimana cara membuatnya. Saudara Christo mengajarkan saya menggunakan kode dengan cara seperti berikut:
GaussJordan.mo
function GaussJordan
input Real [:,:] A;
output Real [:,:] B;
protected // untuk local variable
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
//fungsi input A dan output B
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Mencari baris terbawah yang mempunyai nilai pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//move ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Tugas 3
Selanjutnya ada tugas 3 dimana saya membuat pr dari buku mengenai trust dan saya membuat pseucodenya seperti berikut yang dijalankan dalam openmodelica
OpenModelica
Truss
class PR3
parameter Integer N=8; //Bentuk Matrix, 2 titik bertemu
parameter Real A=0.001;// luas cross section truss
parameter Real E=200e9;//Modulus Elastisitas
Real Kg[N,N];
Real Kginitial[N,N];
Real Sol[N];
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N];
Real SolMat[N,1];
Real XMat[N,1];
Real L1=1;
Real L2=1;
Real L3=1.6;
Real L4=1.25;
Real L5=1.6;
Real Tetha1=functiondegtorad(0);//Diperoleh dari perhitungan
Real Tetha2=functiondegtorad(0);//Diperoleh dari perhitungan
Real Tetha3=functiondegtorad(231.34);//Diperoleh dari perhitungan
Real Tetha4=functiondegtorad(270);//Diperoleh dari perhitungan
Real Tetha5=functiondegtorad(308.66);//Diperoleh dari perhitungan
//Boundary
Integer b1=1;
Integer b2=3;
//Truss 1
Real X1=Tetha1;
Real k1=A*E/L1;
Real K1[4,4];
Integer p1x=1;
Integer p1y=2;
Real Kg1[N,N];
//Truss 2
Real X2=Tetha2;
Real k2=A*E/L2;
Real K2[4,4];
Integer p2x=2;
Integer p2y=3;
Real Kg2[N,N];
//Truss 3
Real X3=Tetha3;
Real k3=A*E/L3;
Real K3[4,4];
Integer p3x=2;
Integer p3y=4;
Real Kg3[N,N];
//Truss 4
Real X4=Tetha4;
Real k4=A*E/L4;
Real K4[4,4];
Integer p4x=1;
Integer p4y=4;
Real Kg4[N,N];
//Truss 5
Real X5=Tetha5;
Real k5=A*E/L5;
Real K5[4,4];
Integer p5x=3;
Integer p5y=4;
Real Kg5[N,N];
algorithm
//Pembuatan K Global
K1:=Matrix(X1);
Kg1:=k1*Lokal(K1,N,p1x,p1y);
K2:=Matrix(X2);
Kg2:=k2*Lokal(K2,N,p2x,p2y);
K3:=Matrix(X3);
Kg3:=k3*Lokal(K3,N,p3x,p3y);
K4:=Matrix(X4);
Kg4:=k4*Lokal(K4,N,p4x,p4y);
K5:=Matrix(X5);
Kg5:=k5*Lokal(K5,N,p5x,p5y);
Kg:=Kg1+Kg2+Kg3+Kg4+Kg5;
Kginitial:=Kg;
//Implementing boundary
for i in 1:N loop
Kg[2*b1-1,i]:=0;
Kg[2*b1,i]:=0;
Kg[2*b2-1,i]:=0;
Kg[2*b2,i]:=0;
end for;
Kg[2*b1-1,2*b1-1]:=1;
Kg[2*b1,2*b1]:=1;
Kg[2*b2-1,2*b2-1]:=1;
Kg[2*b2,2*b2]:=1;
//Displacement
Sol:=gaussjordan(N,Kg,X);
//Gaya reaksi
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaksi(N,Kginitial,SolMat,XMat);
end PR3;
Lokal
function Lokal
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Lokal;
Reaksi
function Reaksi input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; output Real Sol[N]; protected Real X[N,1]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaksi;
Matrix
function Matrix
input Real A;
output Real X[4,4];
protected
Real Y;
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Matrix;
functiondegtorad
function functiondegtorad input Real deg; output Real rad; protected constant Real pi = 3.14; algorithm rad:=deg*pi/180; end functiondegtorad;
gaussjordan
function gaussjordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; protected Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end gaussjordan;
QUIZ 2-12-2020
Membuat diagram class dan flowchart dari coding milik saudara Josiah Enrico
Tugas4
Saya mengerjakan tugas 4 menggunakan openmodelica dengan soal sebagai berikut
Rabu,16 Desember 2020
Pada hari ini di dalam kelas metode numerik saya belajar mengenai aplikasi metode numerik dalam kasus optimasi Optimasi dapat dilakukan menggunakan open modelica dengan golden ratio optimation, dapat dilakukan dengan cara: Menentukan batasan titik awal terendah (xL) dan tertinggi (xH) Mendapatkan nilai x1 dan x2 dari golden ratio (d) Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru Mendapatkan nilai x1 dan x2 baru
ssetelah itu kita dapat melakukan coding di openmodelica untuk mendapatkan optimasi, kita menggunakan openmodelica untuk memudahkan kita untuk melakukan optimasi
dan kode yang digunakan untuk openmodelica digunakan untuk melakukan optimasi adalah:
functionobj3 function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:=2*Math.sin(x)-x^2/10; end f_obj3;
dan juga digunakan openmodelica model dimana kode sebagai beriku:
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; �algorithm �xup :=4; xlow:=0; �for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]);
if f1[i]>f2[i] then
xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; �end bracket_optimation3;
Tugas Besar
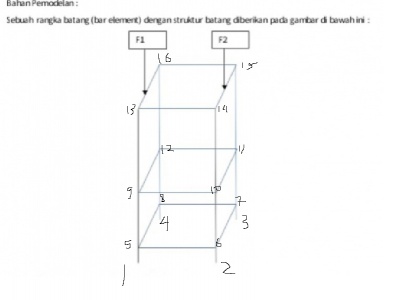
Untuk tugas besar kami diberikan soal berupa: soal seperti dibawah ini
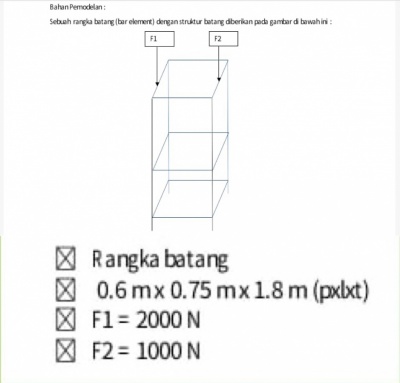pada gambar ini kami disuruh untuk mencari spesifikasi yang paling optimal untuk membuat barang tersebut melalui material, dan juga crosssection dari barang tersebut, dengan menggunakan metode optimasi. dan juga mencari perhitungan seperti reaction, displacement, dan stress.
Perhitungan: dapat diperoleh dari gambar
sehingga diperoleh nodenya.
Selain itu dari dengan diasumsikan menggunakan bahan SS201 siku maka dapat diperoleh
setelah itu dapat dilakukan optimasi sehingga memperoleh
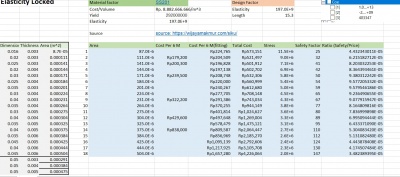
Sehingga diperoleh nilai area sebesar 0.0005013m^2
Selanjut dicari nilai area locked dimana area yang digunakan adalah
selanjutnya dilakukan optimasi sehingga diperoleh
dan diperoleh dari hasil optimasi bahwa nilai dari elastisitas sebesar 197.71 GPa, ini merupakan elasitisitas yang paling efektif untuk bentuk yang dibuat.
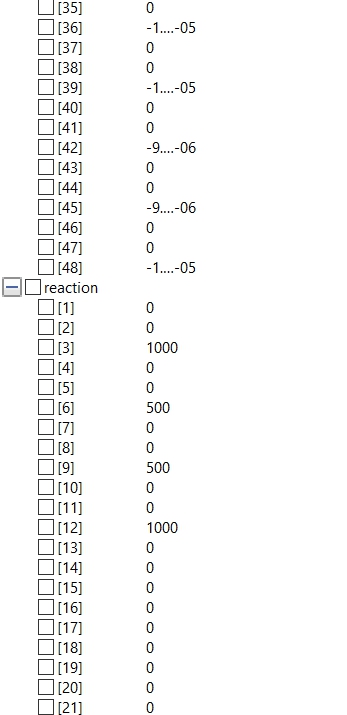
Setelah itu dapat diperoleh displacement dan reaction forcenya dari barang tersebut berupa:
dan diperoleh:
---Open Modelica--- kode open modelica yang saya gunakan dalam perhitungan seperti berikut:
TugasBesar.mo
model Tubesethan //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=292e6; //Yield Strength (Pa) parameter Real Area=0.0005013; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=197.71e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0, 0, 0,1,1,1; //1
0,0.75, 0,1,1,1; //2
0.6,0.75, 0,1,1,1; //3
0.6, 0, 0,1,1,1; //4
0, 0, 0.4,0,0,0; //5
0,0.75, 0.4,0,0,0; //6
0.6,0.75, 0.4,0,0,0; //7
0.6, 0, 0.4,0,0,0; //8
0, 0, 1.1,0,0,0; //9
0,0.75, 1.1,0,0,0; //10
0.6,0.75, 1.1,0,0,0; //11
0.6, 0, 1.1,0,0,0; //12
0, 0, 1.8,0,0,0; //13
0,0.75, 1.8,0,0,0; //14
0.6,0.75, 1.8,0,0,0; //15
0.6, 0, 1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if; end for;
end Tubesethan;
curvefitting.mo
class Curvefitting
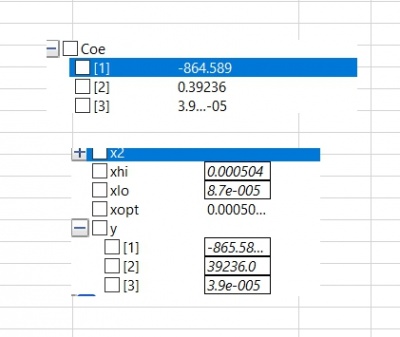
parameter Real X[18]={0.000087, 0.000111, 0.000141, 0.000144, 0.000171, 0.000184, 0.000201, 0.000224, 0.000231, 0.000264, 0.000275, 0.000304, 0.000325, 0.000375, 0.000384, 0.000425, 0.000444, 0.000504}; parameter Real Y[18]={0.0000443, 0.0000621, 0.0000820, 0.0000836, 0.0000938, 0.0000957, 0.0000958, 0.0000923, 0.0000907, 0.0000816, 0.0000783, 0.0000699, 0.0000643, 0.0000530, 0.0000513, 0.0000444, 0.0000417, 0.0000348};
Real Coe[3];
algorithm Coe:=Curve_Fitting(X,Y,2);
end Curvefitting;
fungction curvefitting function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for;
end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting; /* for i in 1:3 loop
for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R);
end for;
optimisation model Opt_Gold
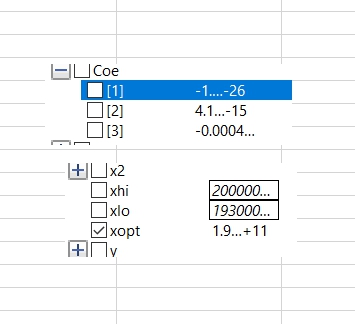
parameter Real[3] y={-1.05119e-26,4.157e-15,0.00041};
parameter Real xlo=193000000000;
parameter Real xhi=200000000000;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo; xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt); if ea[i]<es then
break;
end if; end for;
end Opt_Gold;
UAS
Jawaban uas yang saya lakukan pada hari ini (Rabu,13 Januari 2021)
