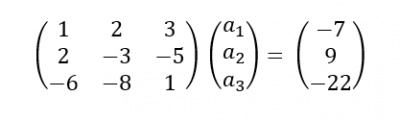Metnum03-Virsya Pramesti Salsabila

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ

Biodata

Nama : Virsya Pramesti Salsabila

NPM : 1806181760

Fakultas/Jurusan : Teknik/Teknik Mesin

Tempat/Tanggal Lahir : Banjarmasin, 21 September 2001

Kelas Metode Numerik-03

Sebelum UTS

Sebelum UTS kami mempelajari cara mencari akar menggunakan dua metode, yaitu bracketing methods dan open methods.

Pada bracketing methods terdapat:

Graphical Methods
metode mencari akar dengan membuat grafik fungsi dan melihat letak perpotongan dengan sumbu x
Bisection Methods
False-Position Methods

Pada open methods terdapat:

Simple Fixed-Point Iteration
Newton-Raphson Methods
Secant Methods
Brent's Method

Setelah itu kita juga mempelajari regresi dan interpolasi linear.

Pertemuan 1 (9 November 2020)

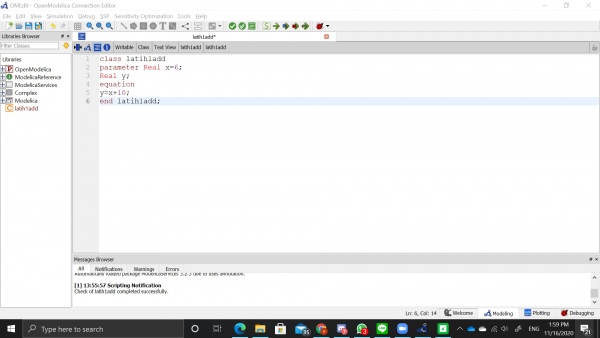
Pada pertemuan pertama ini Pak DAI memulai pembelajaran dengan menjelaskan 4 indikator dasar dalam pembelajaran. Indikator pertama merupakan mengetahui apa yang akan dipelajari dan yang kedua merupakan pemahaman akan konsep yang sudah dipelajari tersebut. Indikator ketiga merupakan memahami pengaplikasian apa yang sudah dipelajari dalam permasalahan yang ditemukan dan indikator terakhir merupakan pengaplikasian apa yang sudah dipelajari dalam diri kita sendiri. Pada akhir kelas kami diminta untuk mempelejari software OpenModelica dan mencoba menggunakan software tersebut. Kami juga diminta untuk menulis pada wikipage serta membuat video mengenai apa yang sudah kita pelajari mengenai OpenModelica.

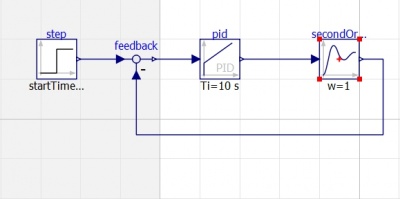
Saya mencoba membuat suatu Feedback Control System simpel dengan bantuan video dari Youtube. Dibawah ini merupakan gambaran block diagram yang saya buat dengan OpenModelica. Dengan bantuan OpenModelica kita dapat mensimulasikan suatu sistem dan software ini akan membuatkan algoritma berdasarkan sistem dan input yang sudah kita buat.

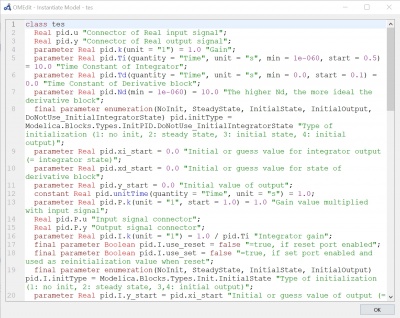
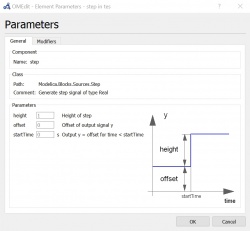
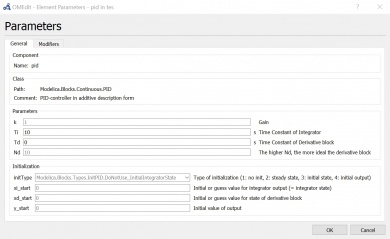
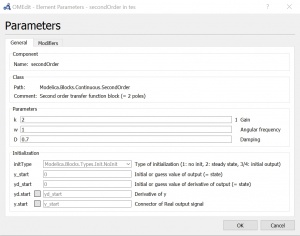
Parameter step function, PID, dan SecondOrder yang saya gunakan terdapat pada foto dibawah ini

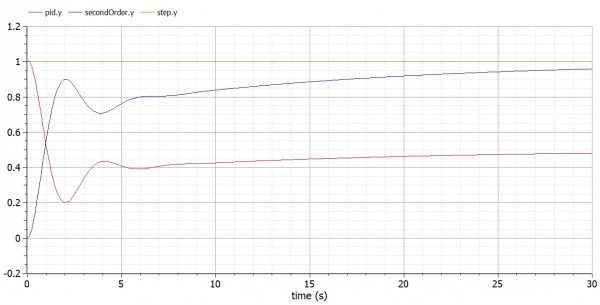
Setelah dilakukan simulasi selama 30 detik, didapatkan grafik output sebagai berikut. Walaupun sudah didapatkan grafik, kita tetap bisa mengubah beberapa variabel dan melakukan simulasi ulang dalam sistem tersebut dan mendapatkan grafik output yang berbeda.

Untuk video penjelasan lebih lengkapnya dapat melihat melalui video yang sudah saya buat:

https://youtu.be/eUP5k0w59BY

Pertemuan 2 (16 November 2020)

Pada pertemuan kedua ini, kelas dimulai dengan pemaparan pemahaman masing-masing mengenai OpenModelica. Setelah itu kami diminta untuk membuat sebuah program sederhana untuk menjumlahkan angka dan juga mencari rata-rata.

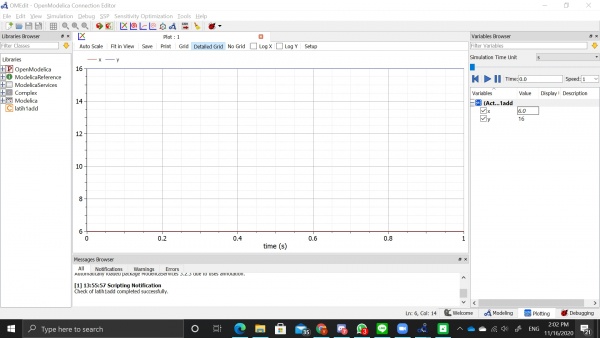
Berikut merupakan algoritma yang saya buat untuk penjumlahan angka

Setelah itu dapat dilihat grafik input dan hasil sebagai berikut, dengan nilai input x=6 didapatkan hasil y=16. Kita juga dapat melakukan simulasi kembali apabila ingin merubah nilai x.

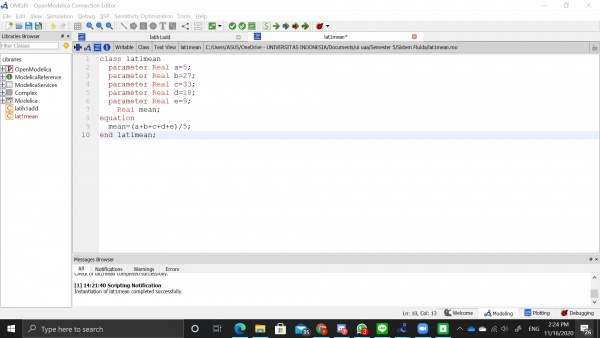
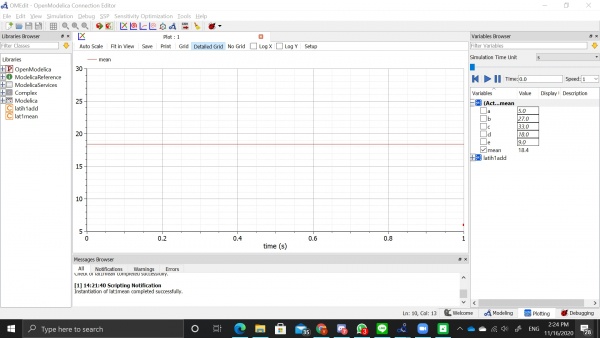
Untuk menghitung rata-rata 5 angka, saya menggunakan algoritma sebagai berikut

Dengan input nilai 5, 27, 33, 18, dan 9 didapatkan hasil mean 18.4 seperti pada grafik dibawah ini.

Tugas - Penyelesaian Persamaan Aljabar Simultan

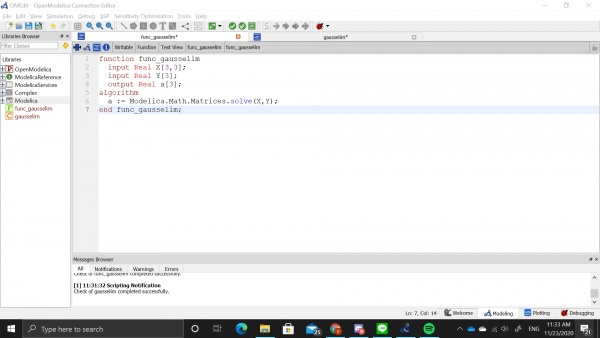
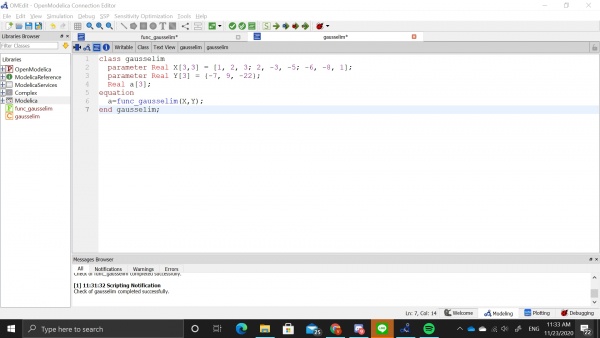
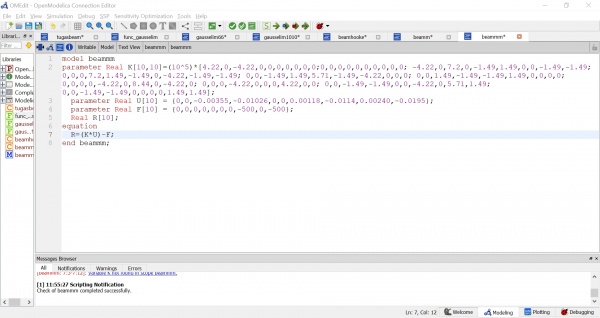
Pada akhir kelas kami diberi tugas untuk membuat suatu program pada OpenModelica untuk menyelesaikan persamaan Aljabar Simultan. Saya menggunakan persamaan aljabar dengan matriks sebagai berikut:

Disini saya menggunakan metode Gauss Elimination. OpenModelica memiliki function yang sudah tersedia untuk menyelesaikan matriks X*a = Y, dimana X merupakan matriks 3 x 3 pada ruas kiri persamaan, Y merupakan hasil dari persamaan yang berada pada ruas kanan persamaan, dan a merupakan nilai yang ingin dicari. Function yang tersedia ini bernama solve dan kita dapat menggunakannya dengan mengetik Modelica.Math.Matrices.solve pada algoritma. Untuk memudahkan eksekusi pada class, saya membuat function terlebih dahulu dengan X dan Y sebagai input serta a sebagai output.

Berikut merupakan class yang saya buat untuk mengeksekusi function terkait:

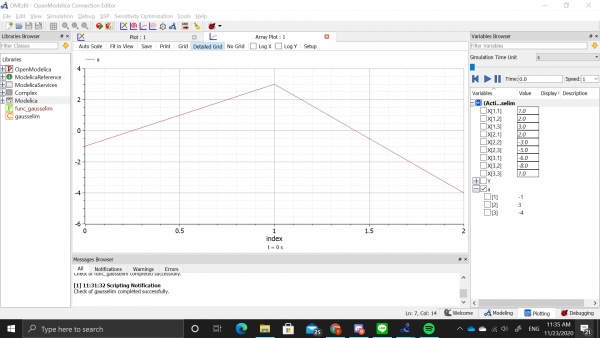
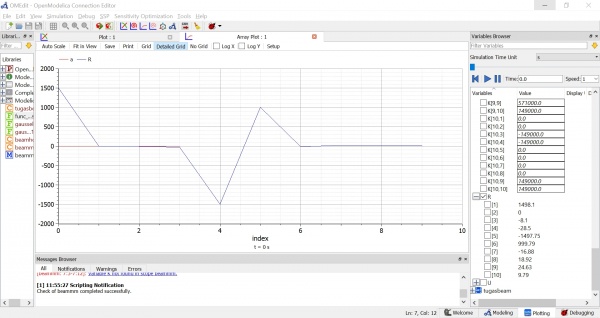
Setelah ini kita dapat menjalankan simulasi untuk mendapatkan hasil dan grafik. Pada gambar dibawah ini kita dapat mengetahui hasil matriks a, yaitu:

a₁ = -1

a₂ = 3

a₃ = -4

Pertemuan 3 (23 November 2020)

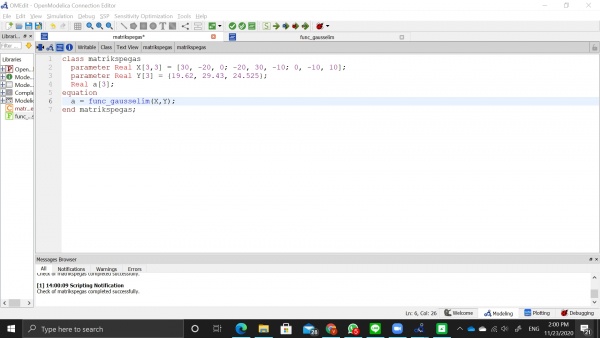
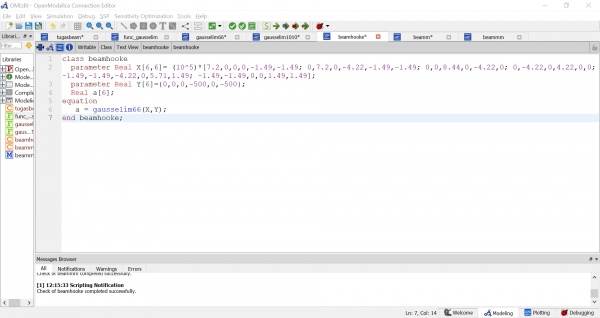
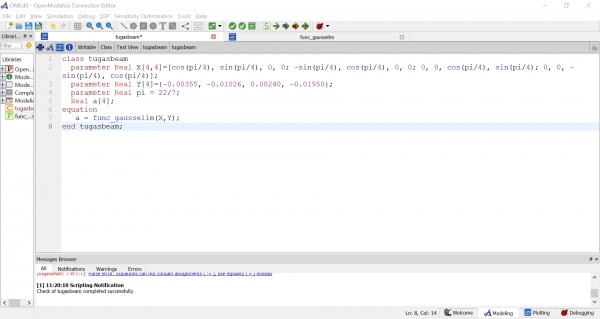
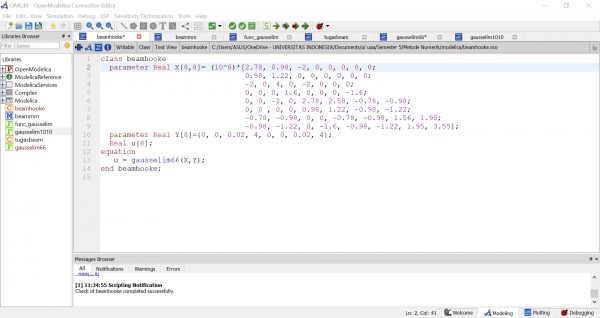
Pada pertemuan ketiga kami diminta untuk menjelaskan tugas minggu lalu yaitu Penyelesaian Persamaan Aljabar Simultan. Setelah itu kami juga diminta untuk membuktikan sebuah persoalan mengenai pegas menggunakan OpenModelica. Disini saya menggunakan function yang sudah saya buat untuk tugas minggu lalu dan membuat class baru sebagai berikut:

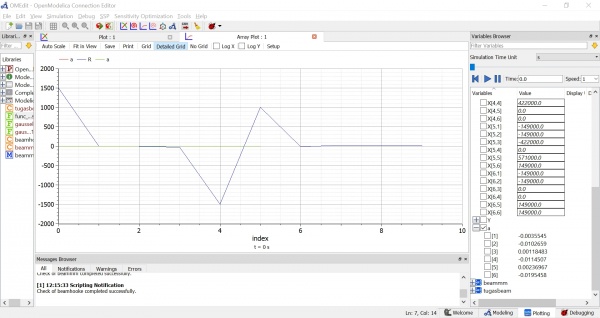
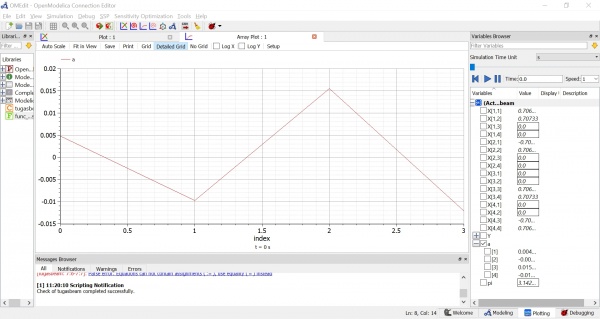
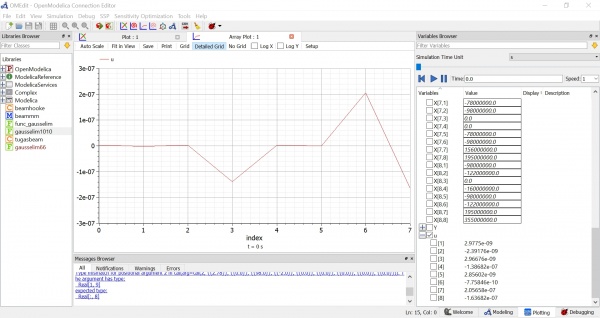
Setelah itu dapat kita lakukan simulasi untuk mendapatkan hasil dan grafik seperti pada gambar dibawah ini. Didapatkan hasil yaitu:

a₁ = 7.3575

a₂ = 10.0552

a₃ = 12.5077

Maka dapat kita simpulkan bahwa jawaban yang tertera pada buku sudah sesuai dengan penyelesaian menggunakan OpenModelica.

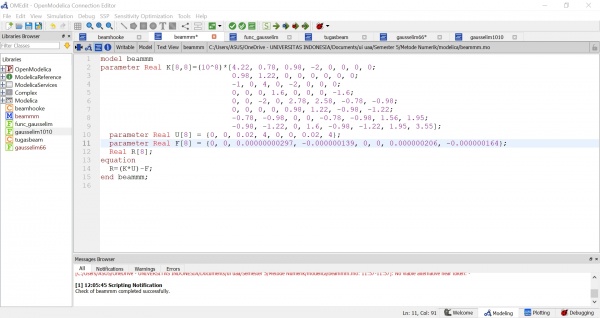
Tugas 1

Pada akhir pertemuan 3 kami diberi tugas untuk menyelesaikan soal dibawah ini.

gambar 1.1

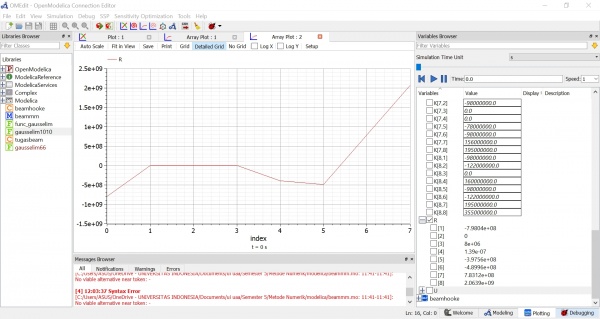
Berikut merupakan hasil simulasi dari class matriks yang saya buat

gambar 1.2

Berikut merupakan hasil simulasi dari model matriks yang saya buat

gambar 1.3

Berikut merupakan hasil simulasi dari class matriks yang saya buat

Pertemuan 4 (30 November 2020)

Pada pertemuan ini Pak Dai menjelaskan kembali mengenai perbedaan statik dan dinamik. Kami juga diminta untuk memahami dan mencoba mensimulasikan algoritma yang sudah dibuat oleh Christo mengenai penyelesaian persamaan menggunakan metode Gauss Jordan

Quiz

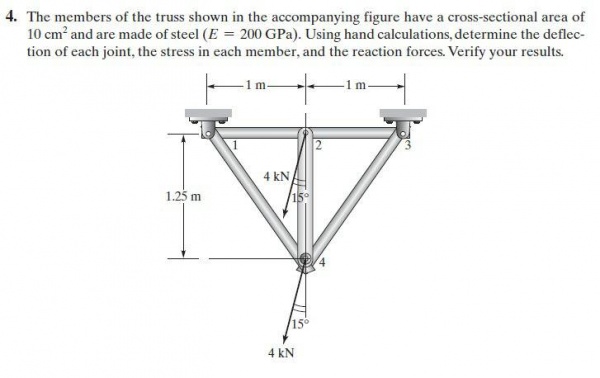
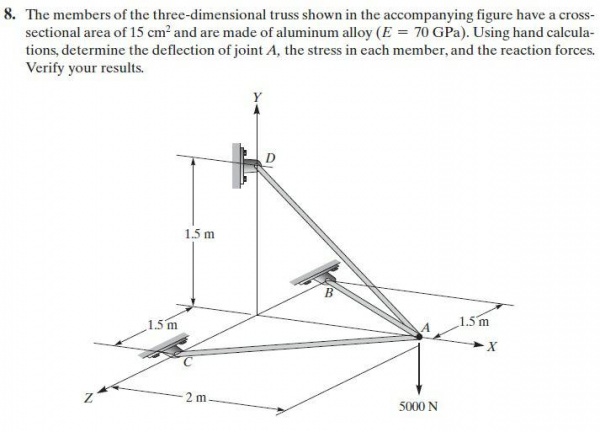
Pada quiz ini kami diminta untuk mengerjakan soal yang tertera pada gambar dibawah ini

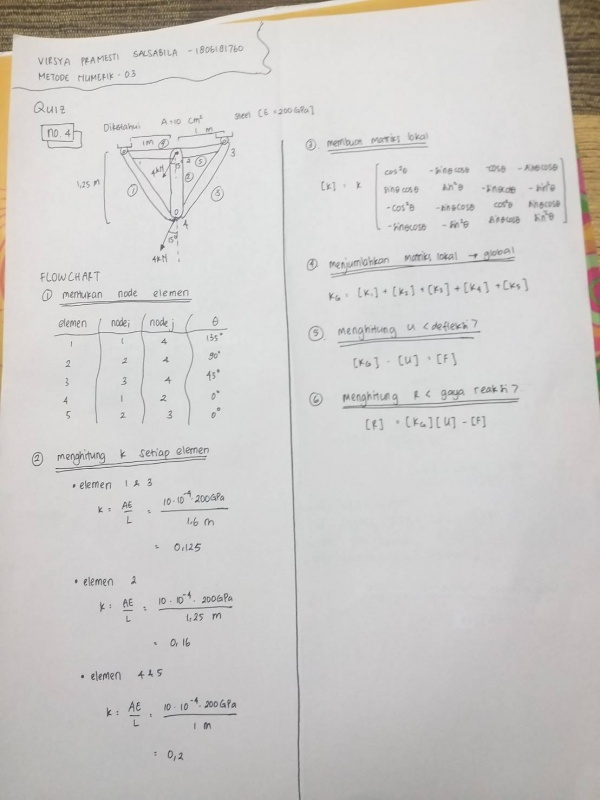
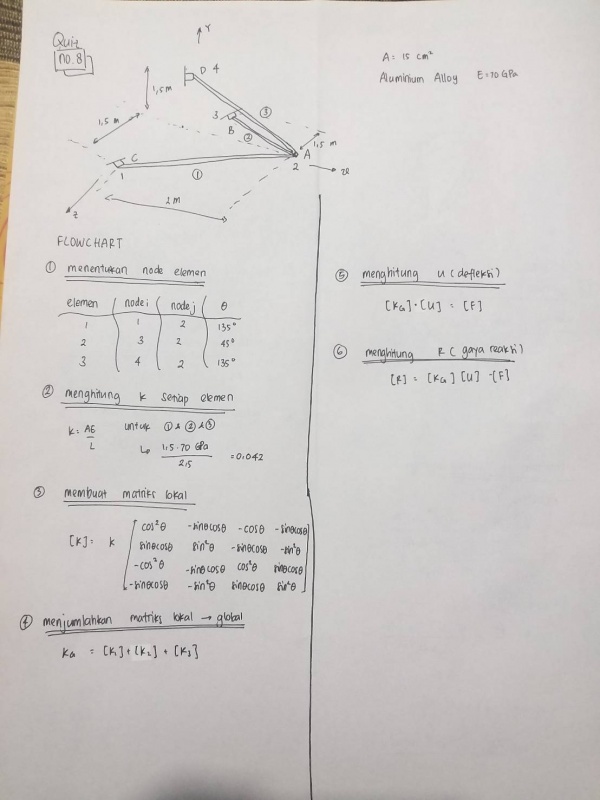
Berikut merupakan flowchart quiz yang saya buat untuk nomor 4 dan 8

Penyelesaian nomor 4

Error creating thumbnail: File with dimensions greater than 12.5 MP

Pertemuan 5 (7 Desember 2020)

Pada pertemuan ini kami membahas quiz yang diberikan minggu lalu dengan mempelajari algoritma yang sudah dibuat dan juga flowchartnya. Pertama-tama teman saya Edward Joshua membantu menjelaskan mengenai langkah pengerjaan soal yang diberikan, kemudian dibantu pula oleh Ahmad Muhammad Fahmi untuk menjelaskan algoritma yang sudah dia buat.

Pada algoritma yang sudah dibuat oleh teman saya, dia menggunakan sistem looping untuk penyelasaian soal quiz yang telah diberikan dengan parameter input A (Luas Permukaan), E (Modulus Elastisitas), node, dan load.

Tugas

1. Mempelajari codingan 3D Fahmi

Pada algoritma soal Quiz No. 4 & 8 Ahmad Muhammad Fahmi, metode yang digunakan untuk penyelesaian sama dengan flowchart yang sudah saya buat untuk Quiz. Penyelesaian kedua soal ini memiliki parameter input A (Luas Permukaan), E (Modulus Elastisitas), node, dan load. Walaupun parameter yang tersedia sama, namun terdapat perbedaan input pada boundary node dikarenakan soal nomor 4 merupakan 2 dimensi dan nomor 8 merupakan 3 dimensi.

Pada algoritma ini dibuat terlebih dahulu beberapa function untuk mempermudah pemanggilan pada class. Disini terdapat function yaitu Stiffness Matrix Global, Sum Stiffness Matrix Global, Boundary Stiffness Matrix Global, Gauss Jordan, Reaction Force, dan Check Force.

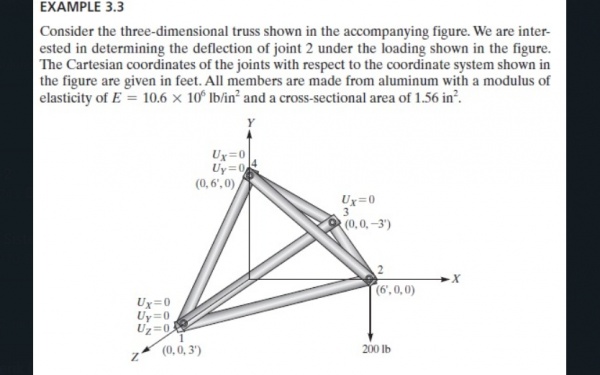
2. Mengaplikasikan pada soal Example 3.3

Berikut merupakan pengaplikasian dari algoritma Fahmi pada Example 3.3

Stiffness Matrix Element Function

 function StiffnessMatrixElement
   input Real [:,6] inisiasi_mat;
   output Real [size(inisiasi_mat,1),6,6] Ke_mat;
 protected
   Real cos_x;
   Real cos_y;
   Real cos_z;
   Real [6] StiffTrig;
   Real [6,6] StiffTrans;
   Real [size(inisiasi_mat,1)] L;
   Real [size(inisiasi_mat,1)] k_vec;
 algorithm
 L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
 k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
 // Finding stiffness matrix of each element member
    for i in 1:size(inisiasi_mat,1) loop
 // Clearing the matrices
    StiffTrig := zeros(6);
    StiffTrans := zeros(6,6);
 // Converting degrees to radians
    cos_x := inisiasi_mat[i,2]/L[i];
    cos_y := inisiasi_mat[i,3]/L[i];
    cos_z := inisiasi_mat[i,4]/L[i];
 // {cos^2, sin^2, sincos}
    StiffTrig := {(cos_x)^2,
                 (cos_y)^2,
                 (cos_z)^2,
                 (cos_x*cos_y),
                 (cos_x*cos_z),
                 (cos_y*cos_z)};
 // Construct stiffness transformation matrix
 StiffTrans := [  StiffTrig[1],    StiffTrig[4],    StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
                  StiffTrig[4],    StiffTrig[2],    StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
                  StiffTrig[5],    StiffTrig[6],    StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
               -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5],    StiffTrig[1],    StiffTrig[4],    StiffTrig[5];
               -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6],    StiffTrig[4],    StiffTrig[2],    StiffTrig[6];
               -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3],    StiffTrig[5],    StiffTrig[6],    StiffTrig[3]];             
 // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
 for m in 1:6 loop
   for n in 1:6 loop
     Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
   end for;
 end for;
 end for;
 end StiffnessMatrixElement;

Stiffness Matrix Global Function

function StiffnessMatrixGlobal
 input Integer x;
 input Integer [:,2] n;
 input Real [:,6,6] Ke_mat; 
 output Real [size(Ke_mat,1),3*x,3*x] Kg_mat;
algorithm
 Kg_mat := zeros(size(Ke_mat,1),3*x,3*x);
 for i in 1:size(Ke_mat,1) loop
   Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
   Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
   Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];

   Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
   Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
   Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];

   Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
   Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
   Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];

   Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
   Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
   Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
 end for;
end StiffnessMatrixGlobal;

Sum Stiffness Matrix Element Function

function SumStiffnessMatrixGlobal
 input Real [:,:,:] Kg_mat;
 output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
  for a in 1:size(Kg_mat,2) loop
   for b in 1:size(Kg_mat,2) loop
     KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
    end for;
   end for;
end SumStiffnessMatrixGlobal;

Boundary Stiffness Matrix Global Function

function BoundaryStiffnessMatrixGlobal
 input Real [:,:] KgTot_met;
 input Integer[:] Boundary_xyz;
 input Integer[:] Boundary_xy;
 input Integer[:] Boundary_xz;
 input Integer[:] Boundary_yz;
 input Integer[:] Boundary_x;
 input Integer[:] Boundary_y;
 input Integer[:] Boundary_z;
 output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
 
algorithm
 for a in 1:size(KgTot_met,1) loop
   for b in 1:size(KgTot_met,1) loop
    KgB_met[a,b] := KgTot_met [a,b];
   end for;
  end for; 
 
 if Boundary_xyz[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_xyz,1) loop
   for b in 0:2 loop
     KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
     KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
   end for;
  end for;
 end for;
 end if;

 if Boundary_xy[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_xy,1) loop
   for b in 1:2 loop
     KgB_met[3*(Boundary_xy[a])-b,i]:=0;
     KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
   end for;
  end for;
 end for;
 end if;
 
 if Boundary_xz[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_xz,1) loop
   for b in 0:2:2 loop
     KgB_met[3*(Boundary_xz[a])-b,i]:=0;
     KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
   end for;
  end for;
 end for;
 end if;
 
 if Boundary_yz[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_yz,1) loop
   for b in 0:1 loop
     KgB_met[3*(Boundary_yz[a])-b,i]:=0;
     KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
   end for;
  end for;
 end for;
 end if;
 
 if Boundary_x[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_x,1) loop
   KgB_met[3*(Boundary_x[a])-2,i]:=0;
   KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
  end for;
 end for;
 end if;
 
 if Boundary_y[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_y,1) loop
   KgB_met[3*(Boundary_y[a])-1,i]:=0;
   KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
  end for;
 end for;
 end if;
 
 if Boundary_z[1] <> 0 then
 for i in 1:size(KgTot_met,1) loop
  for a in 1:size(Boundary_z,1) loop
     KgB_met[3*Boundary_z[a],i]:=0;
     KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
  end for;
 end for;
 end if;
end BoundaryStiffnessMatrixGlobal;

Gauss Jordan Function

function GaussJordan
 input Real [:,:] KgB_met;
 input Real [size(KgB_met,1)] load_met;
 output Real [size(KgB_met,1)] U_met;
 
 protected
 Real float_error = 10e-10;

algorithm
 U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);

 for i in 1:size(KgB_met,1) loop
   if abs(U_met[i]) <= float_error then
    U_met[i] := 0;
   end if;
 end for;

end GaussJordan;

Reaction Force Function

function ReactionForce
 input Real [:,:] KgTot_met;
 input Real [size(KgTot_met,1)] U_met;
 input Real [size(KgTot_met,1)] load_met;
 output Real [size(KgTot_met,1)] R_met;
 protected Real float_error = 10e-10;

algorithm
 R_met := KgTot_met*U_met-load_met;
 
 for t in 1:size(KgTot_met,1) loop
   if abs(R_met[t]) <= float_error then
     R_met[t] := 0;
   end if;
 end for;
 
end ReactionForce;

Check Force Function

function CheckForce
 input Real [:] load;
 input Real [size(load,1)] R;
 output Real [3] F;
 protected Real float_error = 10e-10;
 
 protected
   Real load_x;
   Real load_y;
   Real load_z;
   Real R_x;
   Real R_y;
   Real R_z;
   
algorithm
 load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
 load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
 load_z := sum({load[i] for i in 3:3:size(load,1)});
 R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
 R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
 R_z := sum({R[i] for i in 3:3:size(load,1)});
 
 F[1] := load_x + R_x;
 F[2] := load_y + R_y;
 F[3] := load_z + R_z;
 
 for i in 1:3 loop
   if abs(F[i]) <= float_error then
    F[i] := 0;
   end if;
 end for;

end CheckForce;

Berikut merupakan class yang digunakan untuk memanggil function diatas dan menyelesaikan Example 3.3

Class

class QuizSoal1
 //inisiasi = [ elemen#, dX, dY, dZ, A, E]
 parameter Real [:,6] inisiasi = [1,  6,  0, -3, 1.56, 10.6e6; //isi sesuai data
                                  2,  0,  0, -6, 1.56, 10.6e6;
                                  3,  0,  6, -3, 1.56, 10.6e6;
                                  4, -6,  0, -3, 1.56, 10.6e6;
                                  5, -6,  6,  0, 1.56, 10.6e6;
                                  6,  0,  6,  3, 1.56, 10.6e6];

 //node = [ i, j]                                 
 parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
                                                1, 3;
                                                1, 4;
                                                2, 3;
                                                2, 4;
                                                3, 4];

 //jumlah node
 parameter Integer n = 4; //isi sesuai data

 //titik node boundary xyz
 parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data

 //titik node boundary xy
 parameter Integer [:] Boundary_xy = {4}; //isi sesuai data

 //titik node boundary xz
 parameter Integer [:] Boundary_xz = {0}; //isi sesuai data

 //titik node boundary yz
 parameter Integer [:] Boundary_yz = {0}; //isi sesuai data

 //titik node boundary x
 parameter Integer [:] Boundary_x = {3}; //isi sesuai data

 //titik node boundary y
 parameter Integer [:] Boundary_y = {0}; //isi sesuai data

 //titik node boundary z
 parameter Integer [:] Boundary_z = {0}; //isi sesuai data
                            
 //load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
 parameter Real [3*n] load = {0,    0, 0,  //isi sesuai data
                              0, -200, 0, 
                              0,    0, 0, 
                              0,    0, 0};

 Real [size(inisiasi,1)] L;
 Real [size(inisiasi,1)] k;
 Real [size(inisiasi,1),6,6] Ke;
 Real [size(inisiasi,1),3*n,3*n] Kg;
 Real [3*n,3*n] KgTot;
 Real [3*n,3*n] KgB;
 Real [3*n] U;
 Real [3*n] R;

 //check force
 Real [3] F;

equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};

k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};

Ke = StiffnessMatrixElement(inisiasi);

Kg = StiffnessMatrixGlobal(n, node, Ke);

KgTot = SumStiffnessMatrixGlobal(Kg);

KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);

U = GaussJordan(KgB, load);

R = ReactionForce(KgTot, U, load);

F = CheckForce(load,R);

end QuizSoal1;

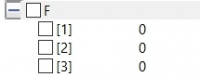
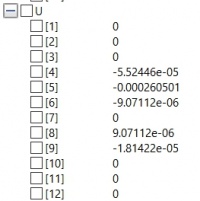
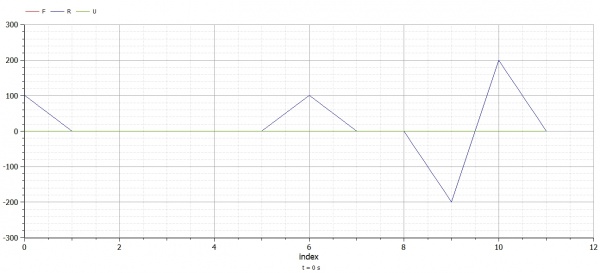
Berikut merupakan hasil dan grafik yang didapat

3. Memberikan masukan atas codingan Fahmi

Menurut saya algoritma yang dibuat Fahmi sudah sangat bagus dan rapi, mungkin untuk mempermudah input kita dapat menambahkan sebuah algoritma tambahan untuk menghitung load dan juga menjadikan E & A sebagai parameter untuk mengurangi kemungkinan kesalahan penulisan pada input matriks pada awal class.

Pertemuan 6 (13 Desember 2020)

Pada pertemuan ini kelas dibuka dengan memahami bahwa yang penting dari pembelajaran adalah pemahaman kami terhadap ilmu dan juga penilaian diri kami akan ilmu yang sudah dipelajari, oleh karena itu kami diminta untuk melakukan muhasabah atas ilmu yang sudah didapat dari kelas metode numerik

Aplikasi Metode Numerik dalam Kasus Optimisasi (21 Desember 2020)

Pada pertemuan ini kami dijelaskan mengenai definisi optimasi dan juga mempelajari metode golden ratio serta menggunakannya dengan OpenModelica dengan bantuan dari Bu Candra

Berikut merupakan program yang digunakan dalam simulasi Open Modelica Golden Ratio Methods

model bracket_optimation3
 parameter Integer n=8;
 Real x1 [n];
 Real x2 [n];
 Real xup;
 Real xlow;
 Real d;
 Real f1 [n];
 Real f2 [n];
 Real xopt;
 Real yopt;
algorithm
 xup  :=4;
 xlow :=0;
 for i in (1:n) loop
 d:=(5^(1/2)-1)/2*(xup-xlow);
 x1[i] := xlow+d;
 x2[i] := xup-d;
 f1[i] := f_obj3(x1[i]);
 f2[i] := f_obj3(x2[i]);
   if f1[i]>f2[i] then
   xup := xup;
   xlow:= x2[i];
   xopt:= xup;
   yopt:= f1[i];
     else
     xlow := xlow;
     xup  := x1[i];
     xopt := xup;
   end if;
 end for;
end bracket_optimation3;

Berikut merupakan function yang digunakan pada program diatas. Algoritma ini disesuaikan dengan permasalahan yang ada.

function f_obj3
 import Modelica.Math;
 input Real x;
 output Real y;
algorithm
 y:=2*Math.sin(x)-x^2/10;
end f_obj3;

Tugas Besar

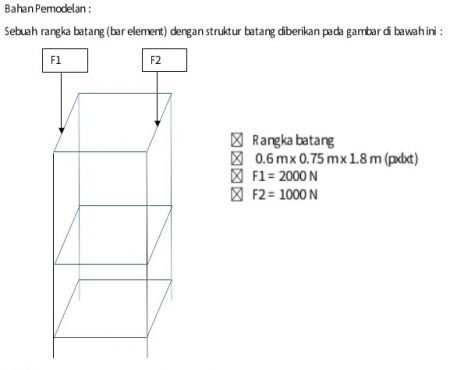
Pada tugas besar ini kami diminta utuk melakukan optimisasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini.

Berikut terlampir file perhitungan saya menggunakan bantuan Excel:

Tugas Besar Metode Numerik_Virsya

Flowchart Pengerjaan Tugas Besar

1. Mendefinisikan Permasalahan

Pada tugas besar ini kami diminta untuk melakukan optimisasi pada rangka untuk mengetahui material apa yang memiliki kekuatan yang maksimal dengan harga yang minimum. Pertama-tama kita harus mengetahui profil dari besi siku dan rangka yang digunakan. Setelah itu kita juga harus menentukan elemen serta node pada rangka.

2. Menentukan Asumsi Kondisi

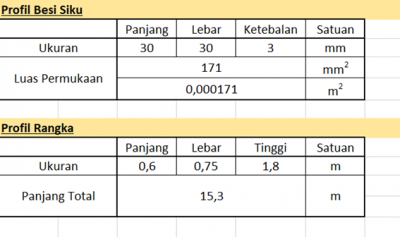
3. Research Data Profil Besi Siku

4. Permodelan Numerik

3D Trusses Model

//define initial variable

  parameter Integer Points=size(P,1);		//Number of Points

  parameter Integer Trusses=size(C,1); 		//Number of Trusses

  parameter Real Yield= (nilai yield) ;		//Yield Strength Material(Pa)

  parameter Real Area= (nilai area) ;   	//Luas Besi Siku (Dimension=30x30x3mm)

  parameter Real Elas= (nilai elastisitas) ;	//Elasticity Material (Pa)

//define connection
parameter Integer C[:,2]=[1,5;  // (Elemen 1)
                         2,6;  // (Elemen 2)
                         3,7;  // (Elemen 3)
                         4,8;  // (Elemen 4)
                         5,6;  // (Elemen 5)
                         6,7;  // (Elemen 6)
                         7,8;  // (Elemen 7)
                         5,8;  // (Elemen 8)
                         5,9;  // (Elemen 9)
                         6,10; // (Elemen 10)
                         7,11; // (Elemen 11)
                         8,12; // (Elemen 12)
                         9,10; // (Elemen 13)
                         10,11;// (Elemen 14)
                         11,12;// (Elemen 15)
                         9,12; // (Elemen 16)
                         9,13; // (Elemen 17)
                         10,14;// (Elemen 18)
                         11,15;// (Elemen 19)
                         12,16;// (Elemen 20)
                         13,14;// (Elemen 21)
                         14,15;// (Elemen 22)
                         15,16;// (Elemen 23)
                         13,16];//(Elemen 24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[   0   ,0  ,0,1,1,1;	//node 1
                          0.75,0  ,0,1,1,1;	//node 2
                          0.75,0.6,0,1,1,1;	//node 3
                          0   ,0.6,0,1,1,1;	//node 4
                          
                          0   ,0  ,0.3,0,0,0;	//node 5
                          0.75,0  ,0.3,0,0,0;	//node 6
                          0.75,0.6,0.3,0,0,0;	//node 7
                          0   ,0.6,0.3,0,0,0;	//node 8
                          
                          0   ,0  ,1.05,0,0,0;	//node 9
                          0.75,0  ,1.05,0,0,0;	//node 10  
                          0.75,0.6,1.05,0,0,0;	//node 11
                          0   ,0.6,1.05,0,0,0;	//node 12
                          
                          0   ,0  ,1.8,0,0,0;	//node 13
                          0.75,0  ,1.8,0,0,0;  //node 14
                          0.75,0.6,1.8,0,0,0;	//node 15
                          0   ,0.6,1.8,0,0,0];	//node 16
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,-1000, 
                          0,0,-500, 
                          0,0,-500, 
                          0,0,-1000}; 
//solution
  Real displacement[N], reaction[N];
  Real check[3];
  Real stress1[Trusses];
  Real safety[Trusses];
  Real dis[3];
  Real Str[3];
protected
 parameter Integer N=3*Points;
 Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 Real err=10e-15, ers=10e-8;
algorithm
 //Creating Global Matrix
    G:=id;
     for i in 1:Trusses loop
		for j in 1:3 loop
 			q1[j]:=P[C[i,1],j];
 			q2[j]:=P[C[i,2],j];
               end for;       
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                    cy*cx,cy^2,cy*cz;
                    cz*cx,cz*cy,cz^2];
   //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;   
 G_star:=G+g;
 G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
 if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
 end if;
end for;
//Solving displacement
    displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
    reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
  check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
  check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
  check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});  
    for i in 1:3 loop
      check[i] := if abs(check[i])<=ers then 0 else check[i];
    end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;       
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];    
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
 for i in 1:Trusses loop
  if stress1[i]>0 then
   safety[i]:=Yield/stress1[i];
  else
   safety[i]:=0;
  end if; 
 end for;
end Trusses_3D_Tugas_Besar;

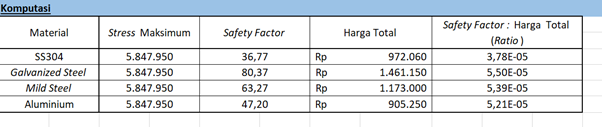
5. Komputasi

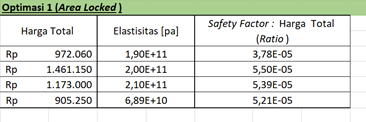
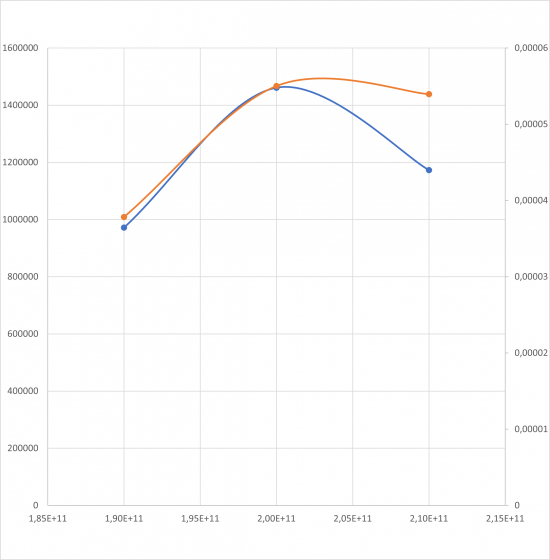
6. Optimasi 1 (Berdasarkan Area Locked)

Berdasarkan grafik diatas dimana terdapat titik perpotongan dari Safety Ratio dan Harga Total, maka material yang paling efektif adalah Galvanized Steel

Referensi

 https://www.jayastainless.co.id/2018/07/19/mengenal-jenis-jenis-logam-stainless-steel-ss201-ss304-ss316-dan-ss430/

 https://abadimetalutama.com/daftar-harga-pipa-kotak-stainless/

 https://wijayamakmur.com/siku/

 https://www.tokopedia.com/aalt-co/siku-aluminium-30x30x3-pjg-6000mm

 http://www.pusatbesibaja.co.id/harga-besi-siku-profil-baja-distributor-pabrik-supplier-agen-jual-toko-produsen/

 https://karinov.co.id/amp/daftar-harga-besi-siku-terbaru/