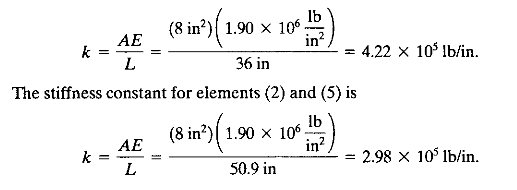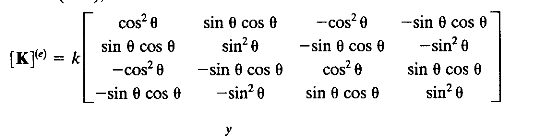Metnum03-Iqbal Reza Alfikri
Nama : Iqbal Reza Alfikri
NPM : 1706104243
Contents
Pertemuan 1
Pada pertemuan 1 Pak Dai menjelaskan tentang 4 poin indikator penilaian yaitu
1. Paham konsep
2. Dapat menerapkan konsep untuk memecahkan persamaan
3. Progress
4. Penilaian diri sendiri
Tugas Pertemuan 1
Hal yang sudah dipelajari sebelum UTS yaitu
1. Deret Mclaurin
2. Open method dan bracketing method
3. Regresi Linear
4. Turunan Numerik
Pada tugas 1 juga ditugaskan untuk membuat video tentang openmodelica
Untuk tugas 1 ini saya menggunakan referensi video ini untuk mensimulasikan ketinggian air pada gelas
https://www.youtube.com/watch?v=OsWNgD43Ib8&t=630s
Dan ini adalah Tugas saya
Pertemuan 2
Pada pertemuan 2, diberikan latihan untuk mencari rata-rata menggunakan looping.
pembelajaran pertemuan 2 tentang class dan function. pada class kita menulis coding untuk di eksekusi kemudian pada fuction adalah tempat dimana memberi perintah dalam bentuk terstruktur seperti proses perhitungan matematik dilakukan di function. function nantinya dapat dipanggil dalam class dengan input yang ditentukan pada class.
Metode looping juga digunakan untuk melakukan operasi eleminasi Gauss-Jordan
Tugas Pertemuan 2
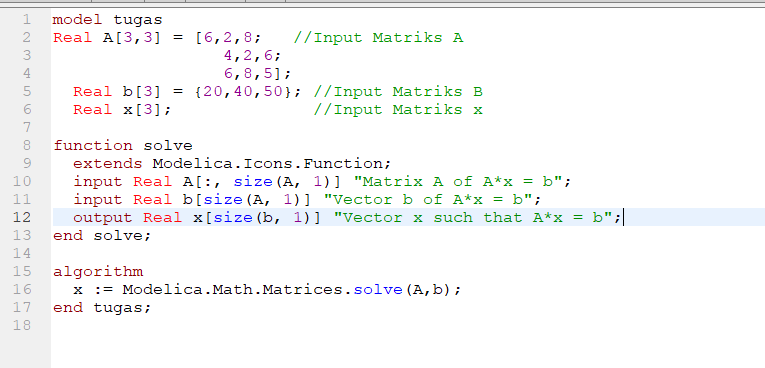
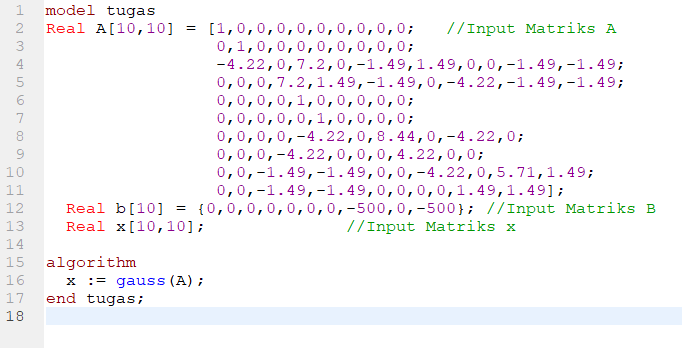
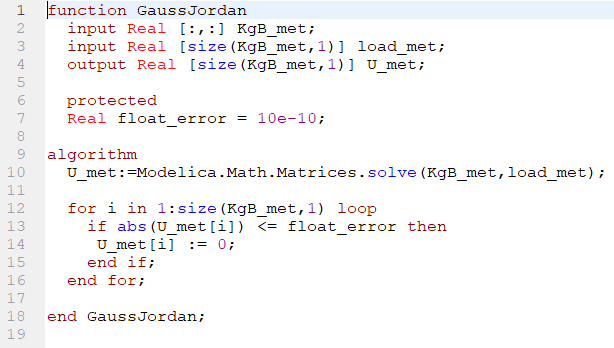
Melalui Openmodelica rupanya tidak diperlukan metode looping untuk melakukan eleminasi Gauss-Jordan. Karena didalam Openmodelica sendiri sudah tersedia fungsi
Modelica.Math.Matrices.solve
yang merupakan fungsi untuk melakukan eleminasi Gauss-Jordan. Sumber laman : https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html
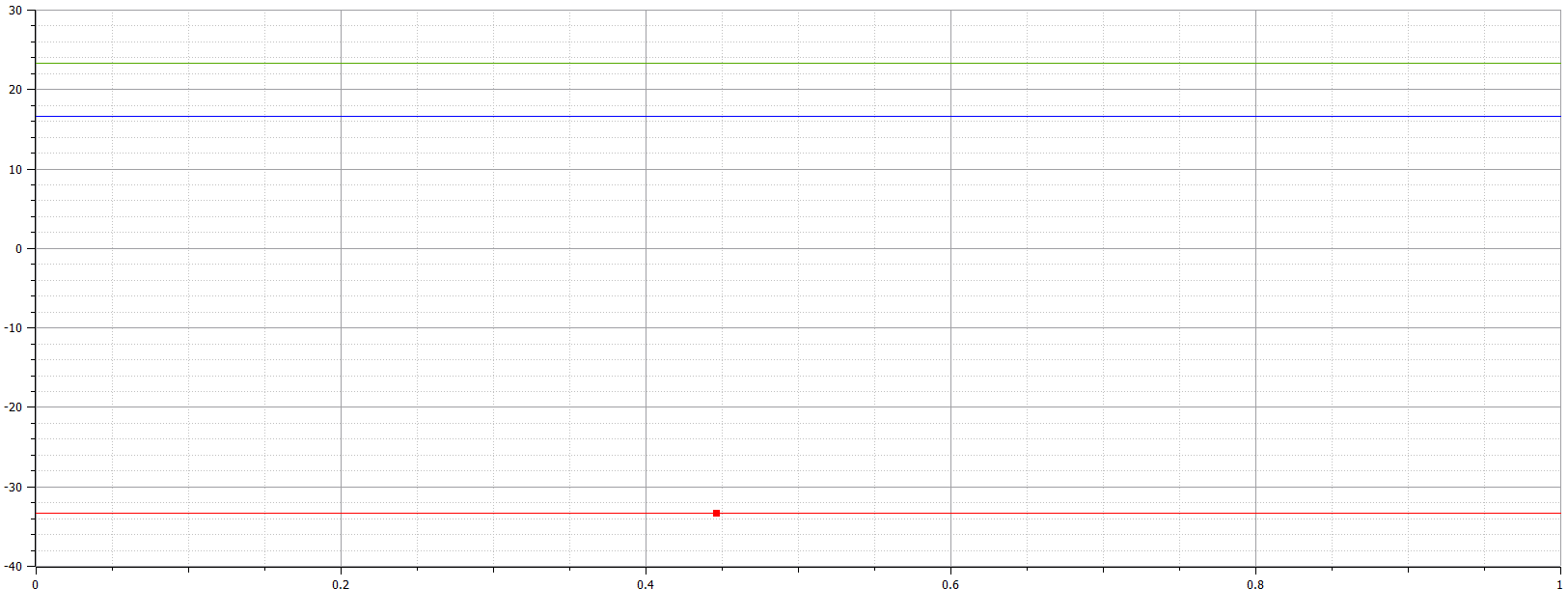
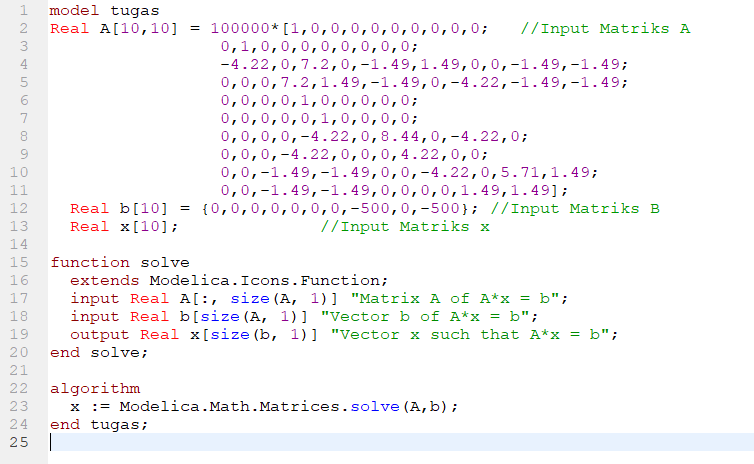
berikut ini adalah contoh penggunaannya
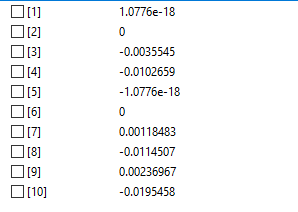
hasilnya didapatkan x sebesar
Pertemuan 3
Dalam pertemuan 3 Pak Dai memberikan materi tentang langkah-langkah penyelesaian masalah dalam metode numerik yaitu
Masalah teknik -> Analisis masalah -> Model matematis -> Model numerik -> komputer -> solusi
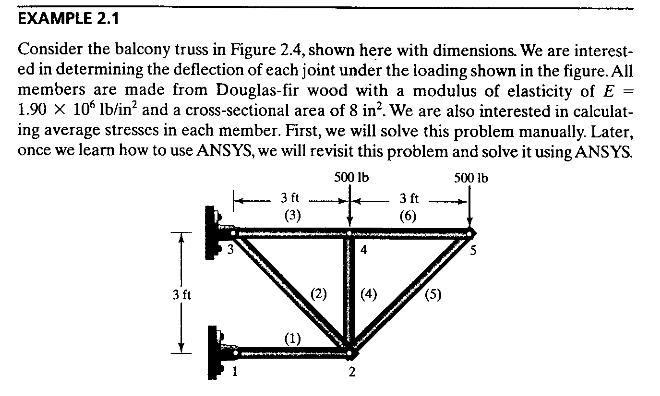
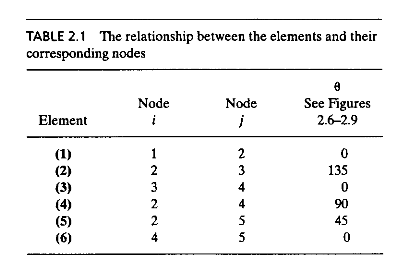
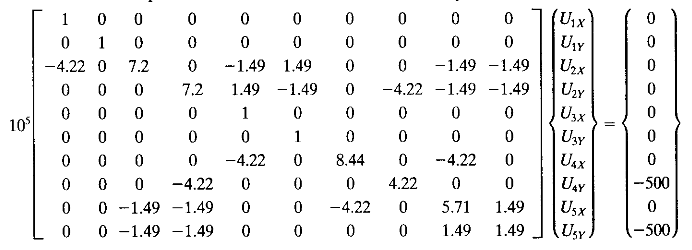
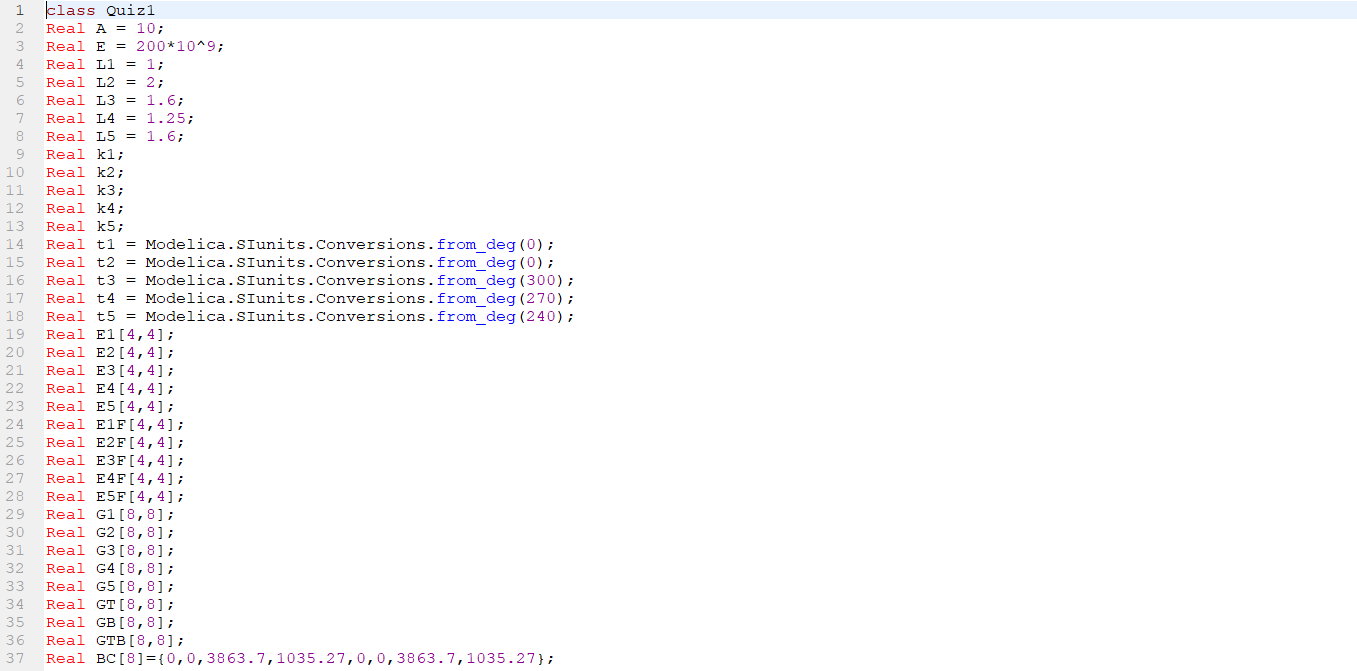
Kemudian untuk tugas Pak Dai memberikan instruksi untuk membuktikan permasalahan yang ada pada buku yaitu persoalan 12.11
Tugas Pertemuan 3
Menyelesaikan soal
1. Memberikan penamaan agar mudah dalam pengerjaan
2. Menghitung k untuk tiap elemen
3. Membuat matriks untuk setiap elemen dengan memasukkan theta kedalam persamaan
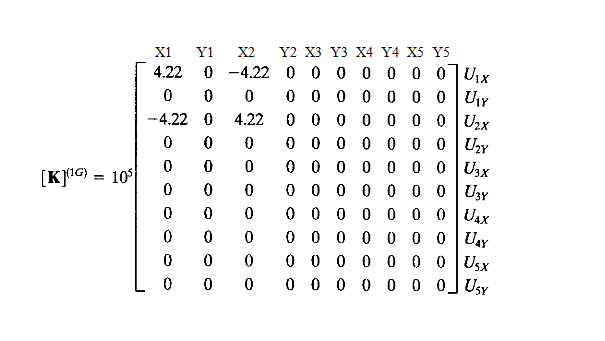
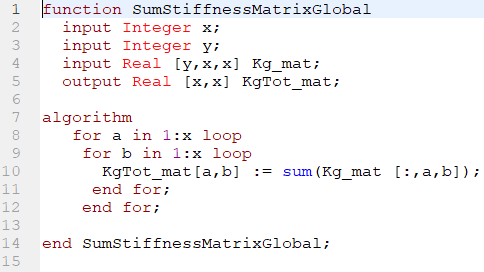
4. Membuat matriks global dari setiap elemen dengan memasukkan matrix dari hasil nomor 3.
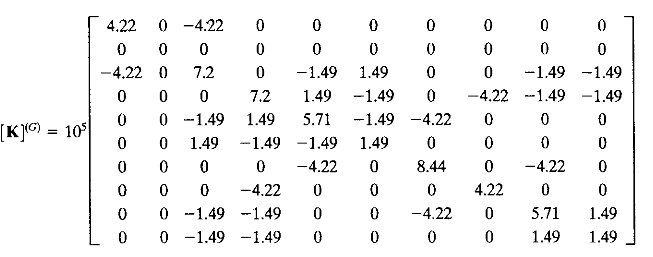
5. Menjumlah semua matrix global dari nomor 4 menjadi matrix global total
6. Menyelesaikan persamaan
7. Hasil
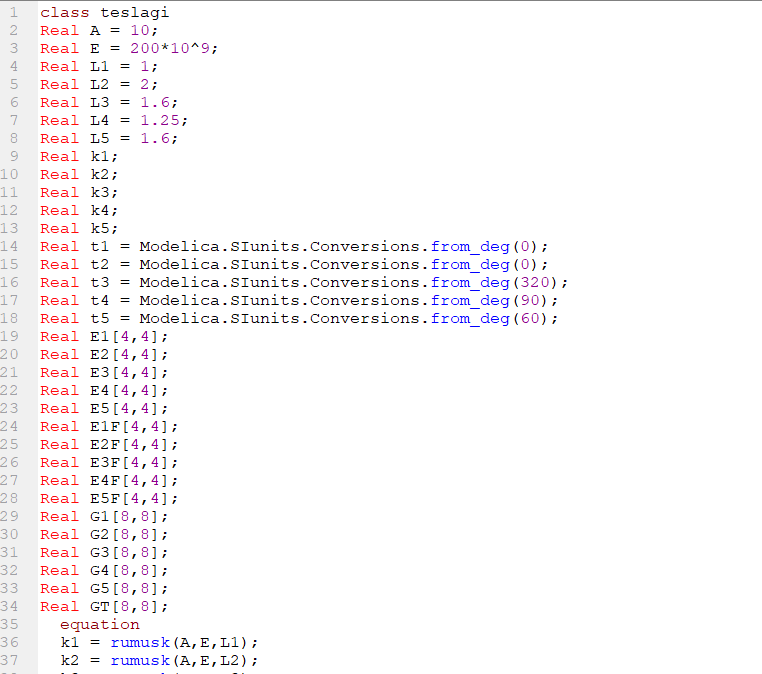
Penyelesaian menggunakan Openmodelica (percobaan pertama)
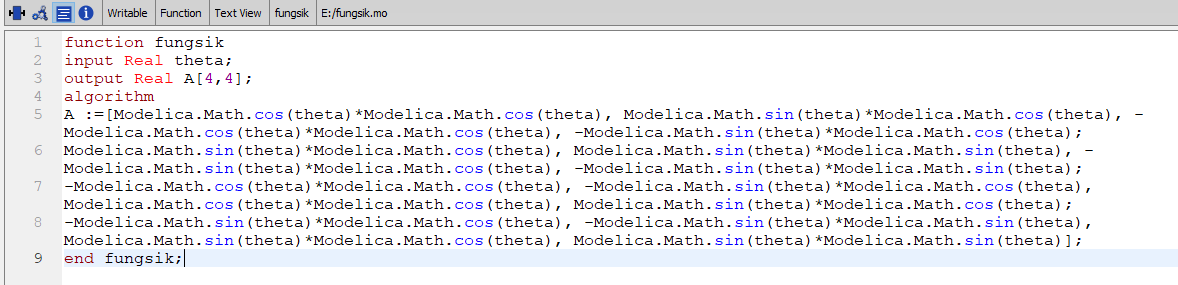
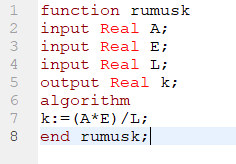
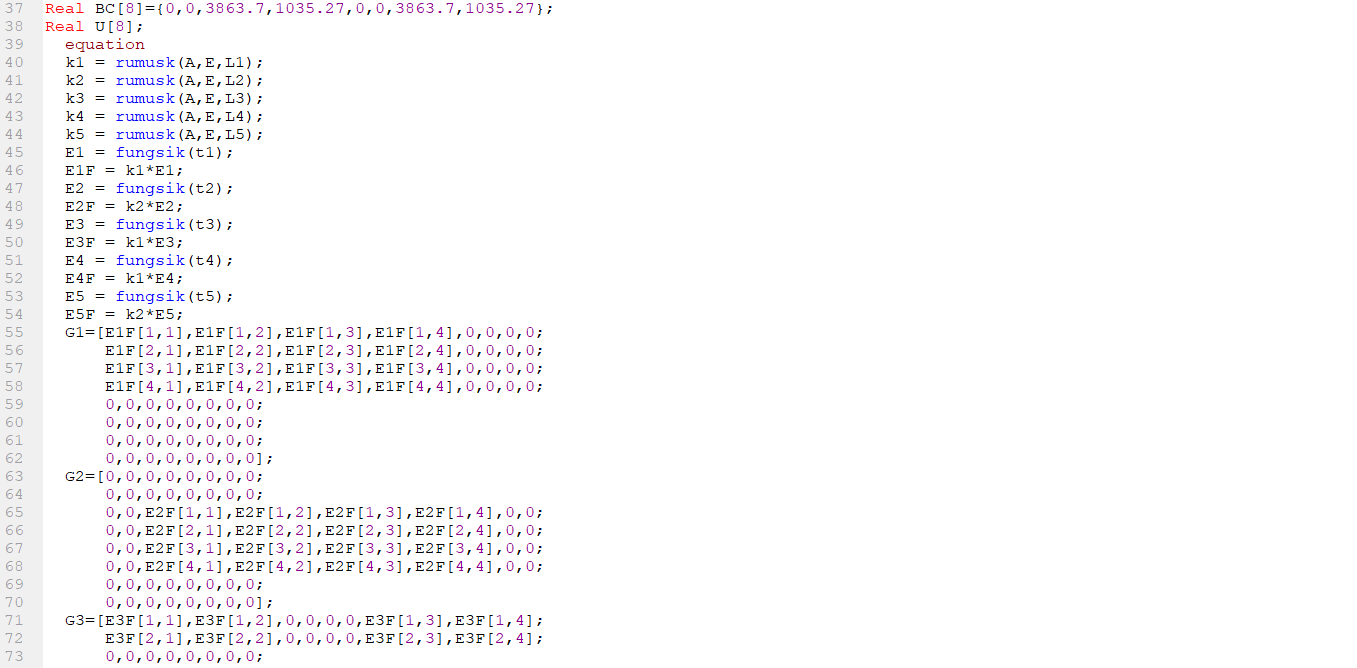
Untuk percobaan pertama saya mencoba untuk membuat fungsi yang saya beri nama fungsik untuk membuat matriks pada nomor 3 diatas secara otomatis
lalu kemudian saya panggil fungsi tersebut kedalam class yang sudah saya buat.
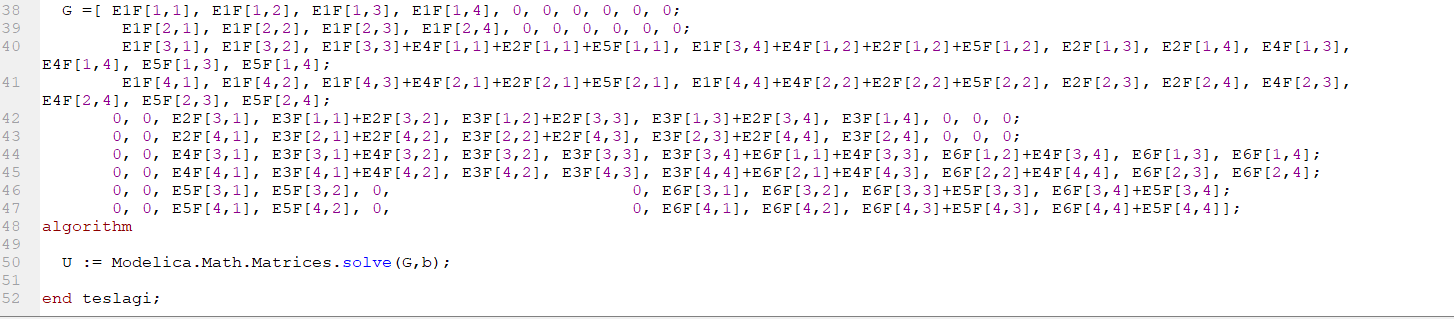
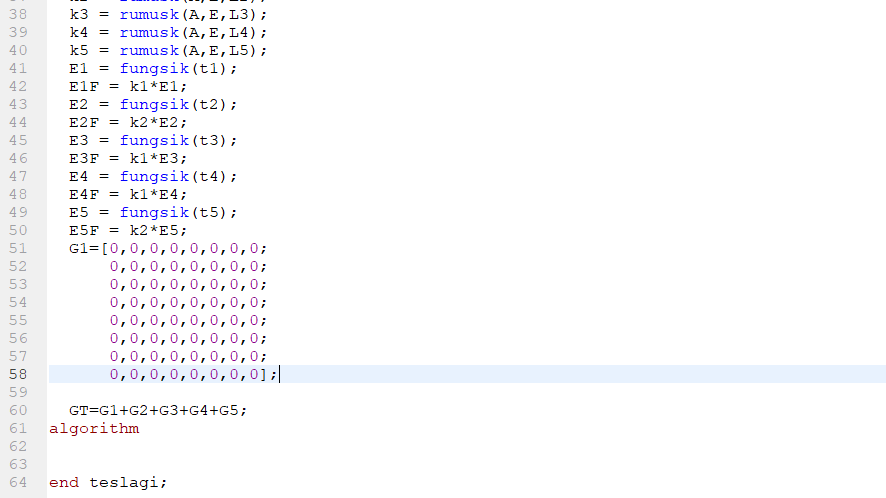
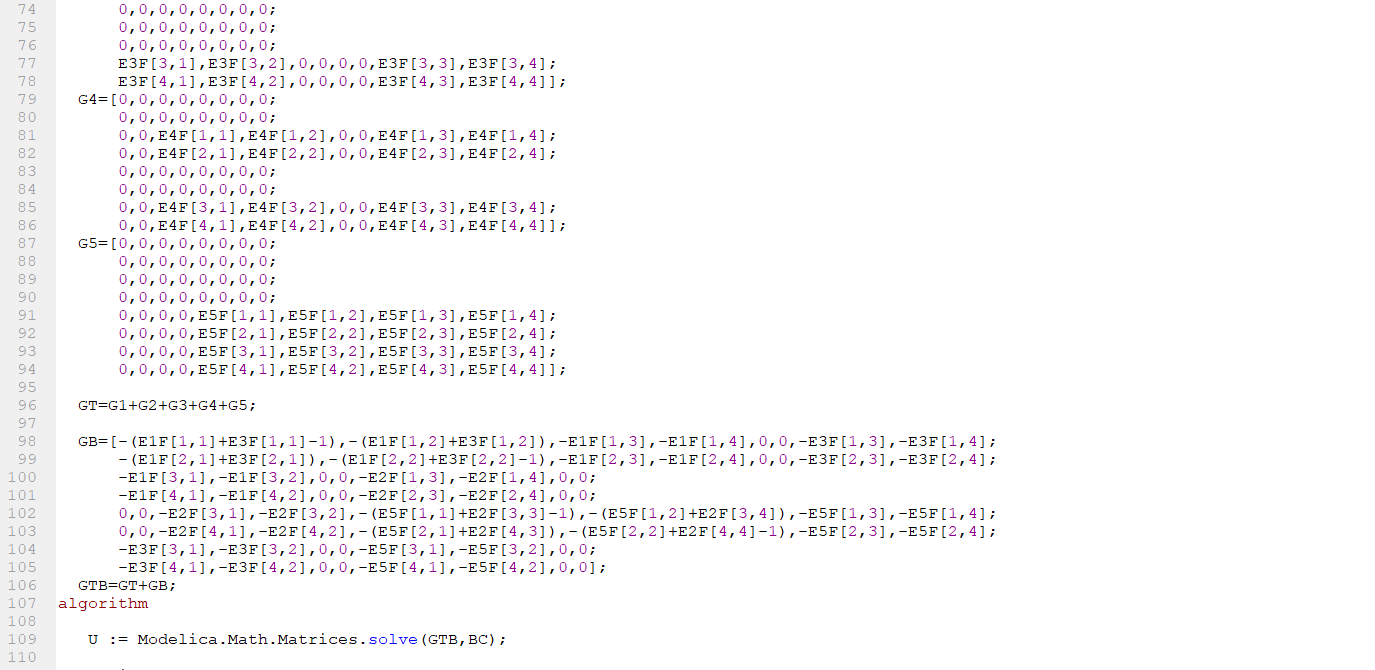
Dalam code ini saya awalnya berharap bahwa saya dapat memasukkan nilai nilai yang berasal dari matriks theta untuk membentuk matriks G[10,10] yang nantinya akan digunakan ke command
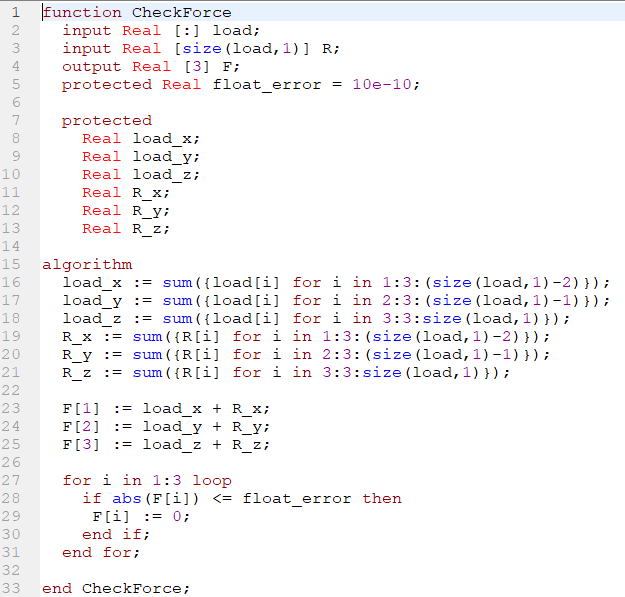
U := Modelica.Math.Matrices.solve(G,b);
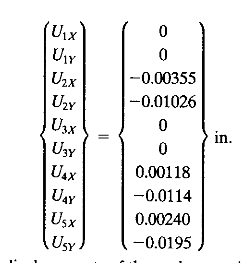
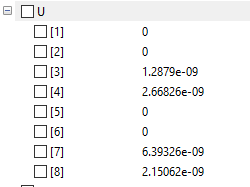
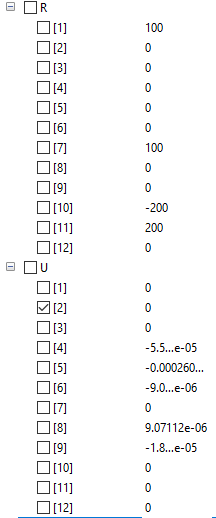
kemudian dari command tersebut akan ditemukan hasil matriks U yaitu displacement pada setiap point.
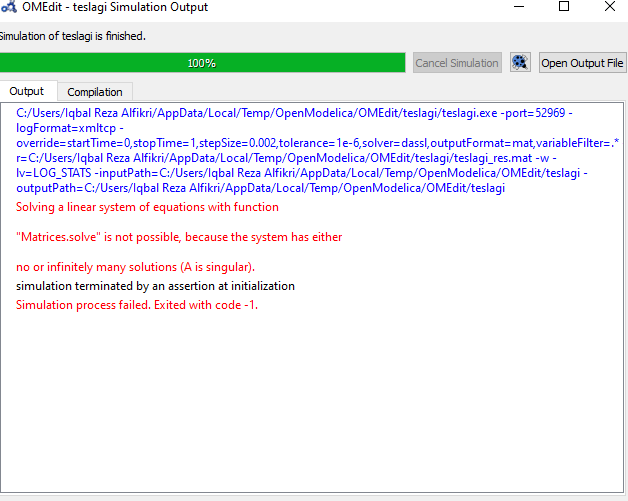
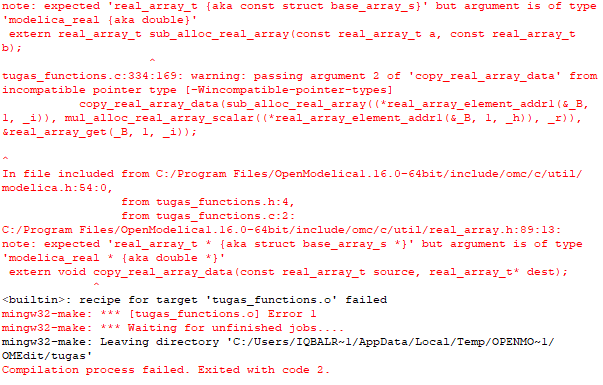
namun setelah saya run terdapat error seperti ini
Error ini terjadi karena matriks k global total belum disederhanakan dan belum diterapkan boundary condition
Penyelesaian menggunakan Openmodelica (percobaan kedua)
untuk penyelesaian yang kedua saya hanya memasukkan matrix global yang sudah dijumlahkan kedalam code dibawah ini
lalu hasilnya adalah seperti ini
perbedaan percobaan pertama dan kedua adalah di percobaan kedua pembuatan matriks dilakukan secara manual dimana percobaan pertama matriks akan dibuatkan secara otomatis.
berikut ini saya sertakan file OME nya.
file function : https://drive.google.com/file/d/1r6ilGSlWuVNzMAPzV1cYiRzwbBkJP2z_/view?usp=sharing
file class percobaan 1 : https://drive.google.com/file/d/1sGoXsNejOVhWAzn1xJtod0iiRMIv0T4d/view?usp=sharing
file class percobaan 2 : https://drive.google.com/file/d/14xWGhnMeWLZJa-P5XOtDtMD5cPt4dKhY/view?usp=sharing
Pertemuan 4
Mencoba fungsi Gauss-Jordan menggunakan loop namun masih error, fungsi tidak bisa dipanggil.
berikut ini adalah code saya
Quiz
berikut ini adalah flowchart code saya yang sedang dalam proses pembuatan
dan ini adalah codenya yang masih dalam pengerjaan
dan berikut ini adalah fungsi baru yang saya tambahkan yaitu fungsi untuk menghitung k
file function k : https://drive.google.com/file/d/1ejpK3AOfFjUyYHkbSPR-bZ4KSyG24UwV/view?usp=sharing
QUIZ Nomor 4
file case nomor 2 : https://drive.google.com/file/d/1IMSU6i-_kH6-0XmpfGw9Ix2KMFK8-29k/view?usp=sharing
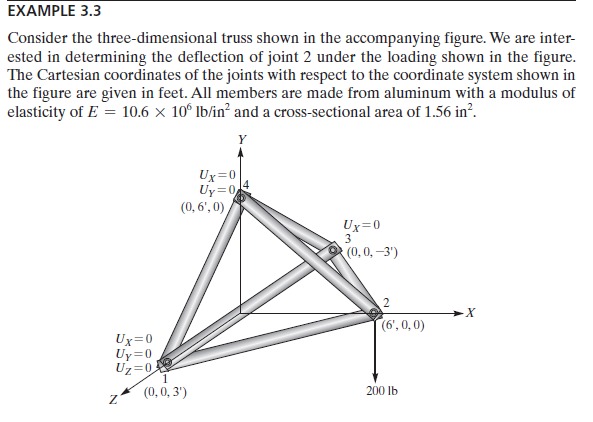
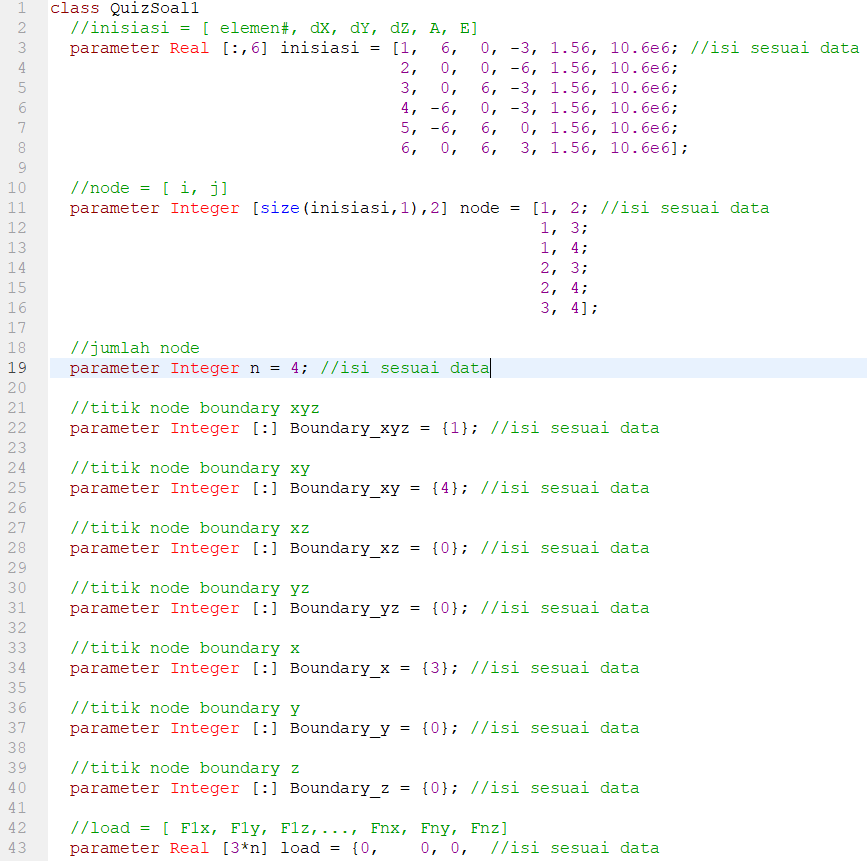
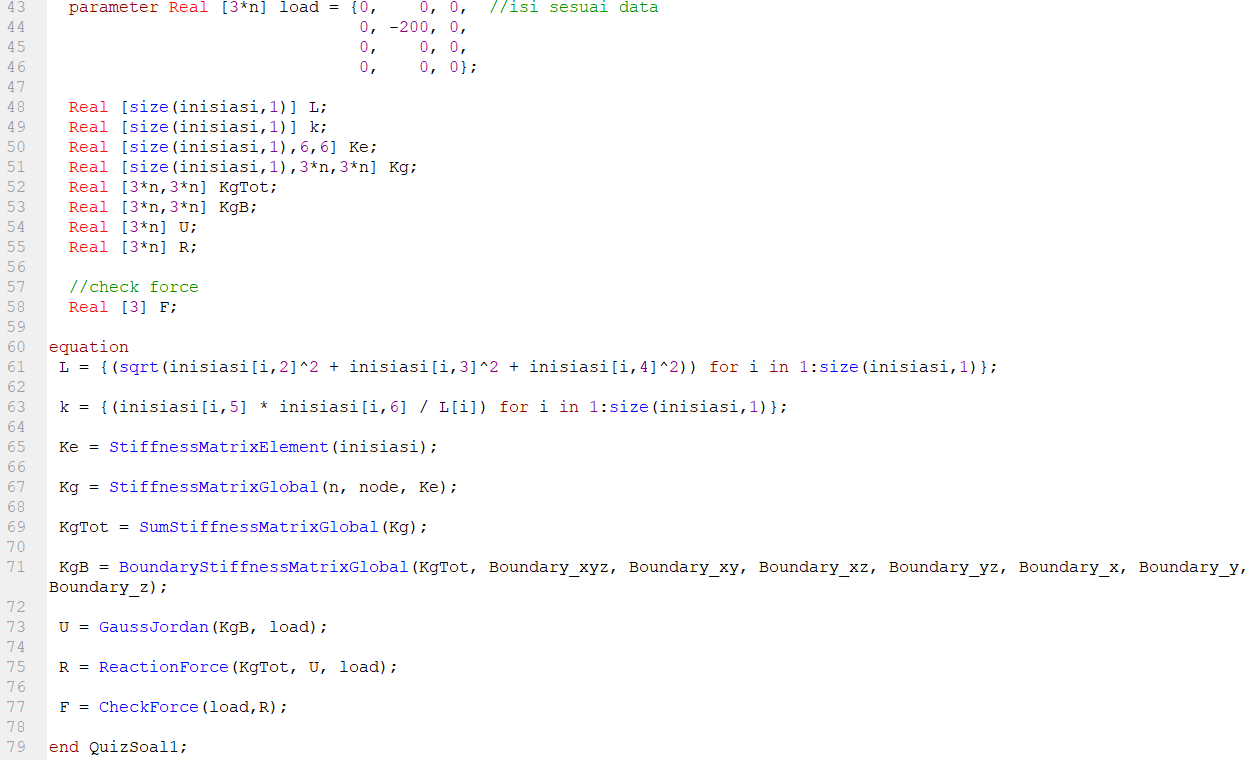
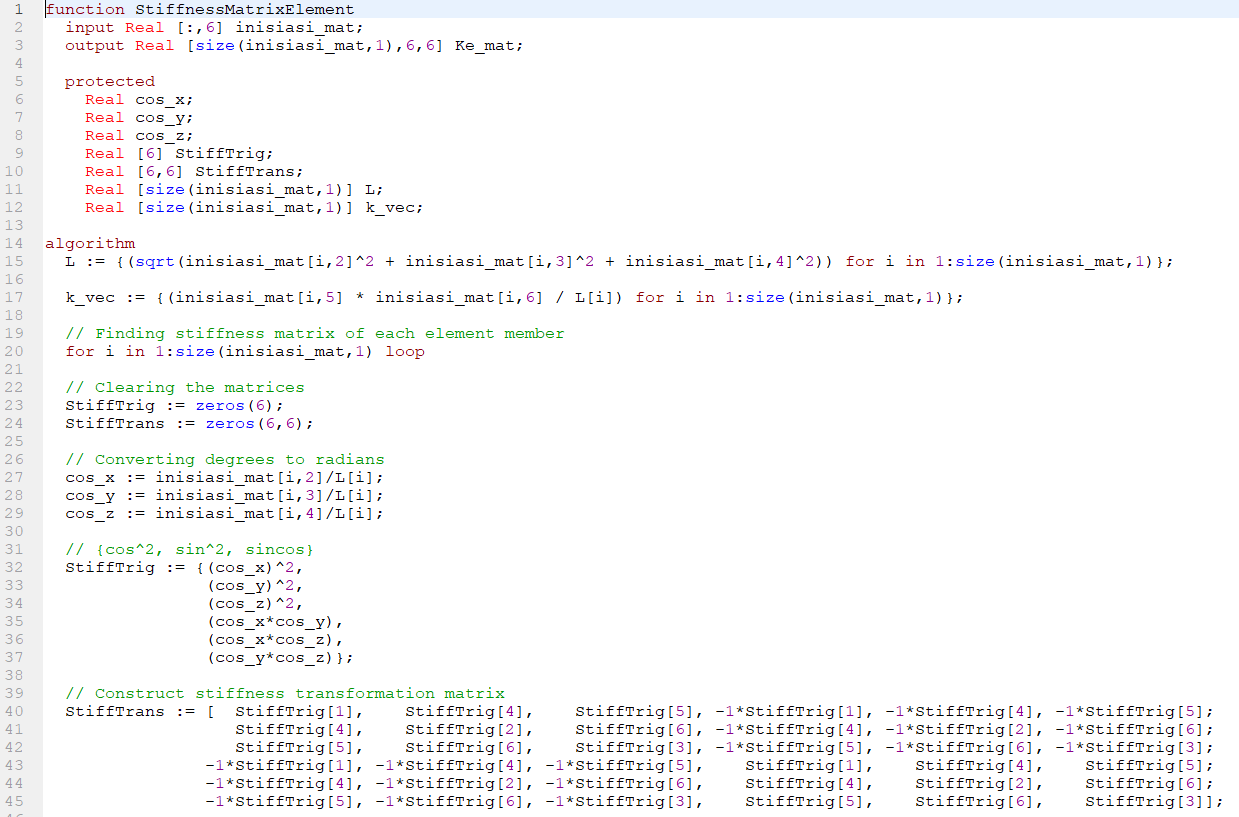
QUIZ Nomor 8
pada analisis yang 3d, pada dasarnya langkahnya sama seperti 2d. Namun, persamaan yang digunakan untuk membuat matrix k berbeda dengan 2d. Dan untuk perhitungan panjang pun berbeda dengan 2d. berikut ini adalah fungsi-fungsi yang saya gunakan pada soal nomor 8.
file fungsi L = https://drive.google.com/file/d/1VDG91gAgRIEFUHuFFzqUfndWj-p1sLtb/view?usp=sharing
Tugas 5
Langkah-langkah
1. Menggunakan class untuk menentukan input dan function yang dipanggil
2. Fungsi K untuk setiap elemen
3. Fungsi K Global
4. Fungsi menjumlahkan matriks K global dari setiap elemen
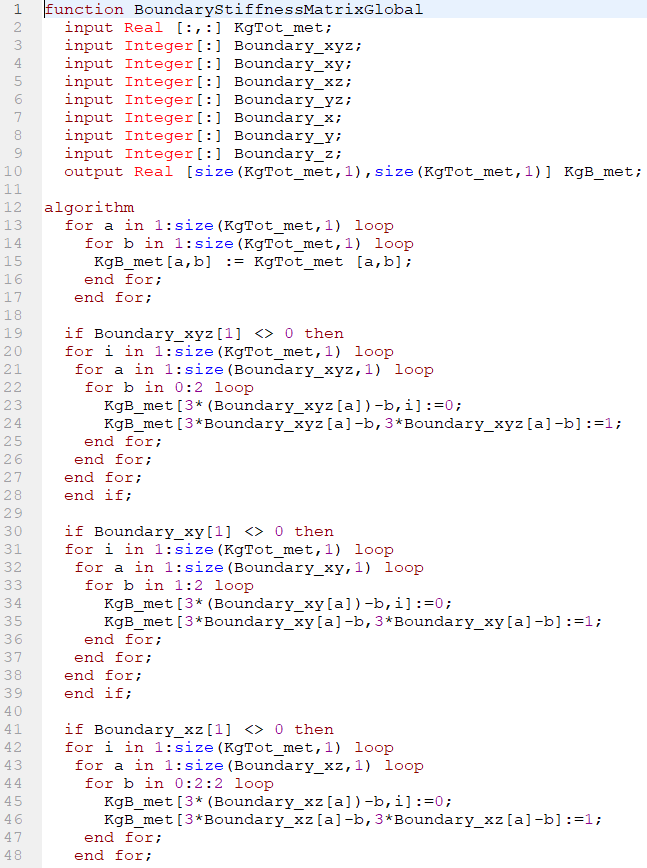
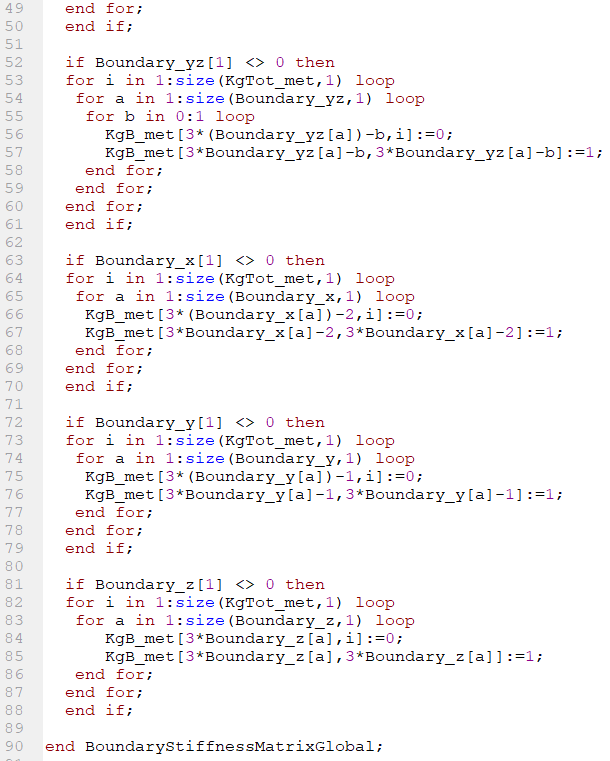
5. Fungsi Boundary Condition
6. Fungsi Gauss Jordan untuk displacement
7. Fungsi menghitung gaya reaksi
8. Fungsi mengecek gaya reaksi
9. Hasil Perhitungan
Pertemuan 6
truss setiap nodal hanya punya 3 derajat kebebasan, variabelnya adalah displacement XYZ.
tujuan untuk meminimalkan biaya
constrain harus cukup tangguh
optimasi harga material yang paling murah
Tugas BEsar
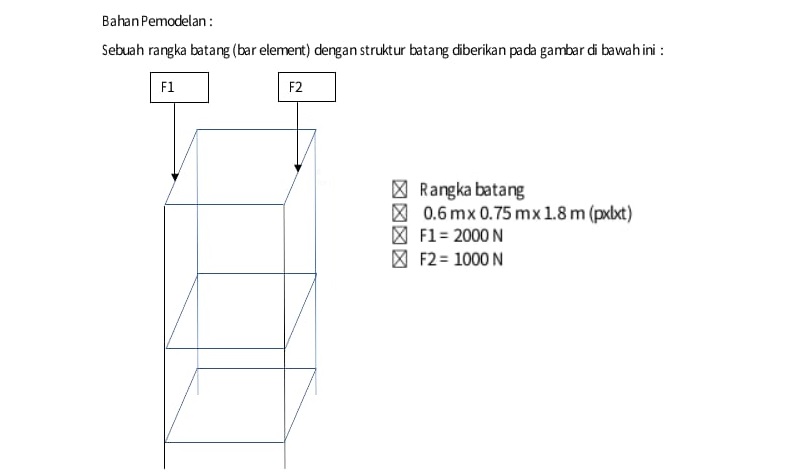
Optimasi pemilihan material dan luas penampang truss
Asumsi :
1. Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
2. Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
3. Safety factor bernilai 2.
4. Batas displacement 0,001 m sebelum buckling(pada kolom paling atas)
Solusi :
Perhitungan stress
//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004)
parameter Real Elas=193e9; //Elasticity SS 304
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
untuk bagian curve fitting
model callcurve
parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4};
parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
Function
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
Program untuk optimasi
model Opt_Gold
parameter Real[3] y={-834.974,0.356007,2.39937e-5};
parameter Real xlo=111e-6;
parameter Real xhi=3.75e-4;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for; end Opt_Gold;
tes