Tugas Besar Metode Numerik (Latihan)- Metode Numerik/23 Desember 2020
Tugas Besar Metode Numerik (Latihan)- Metode Numerik/23 Desember 2020
Objektif:
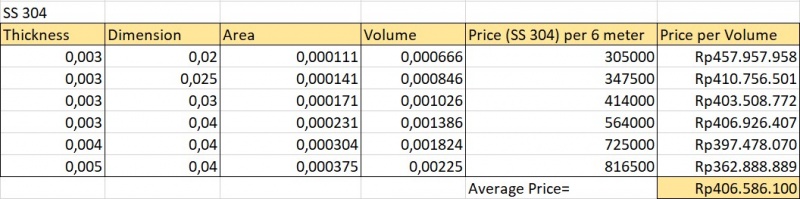
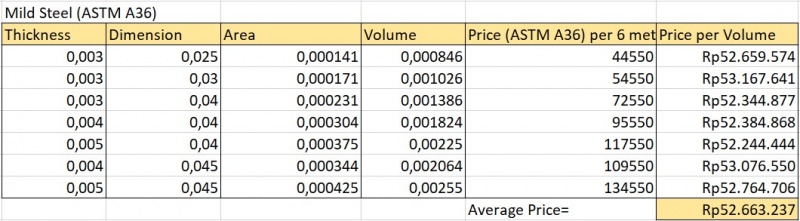
- Mengoptimasi harga pembuatan rangka truss sederhana dengan memvariasi dimensi dan elastisitas material.
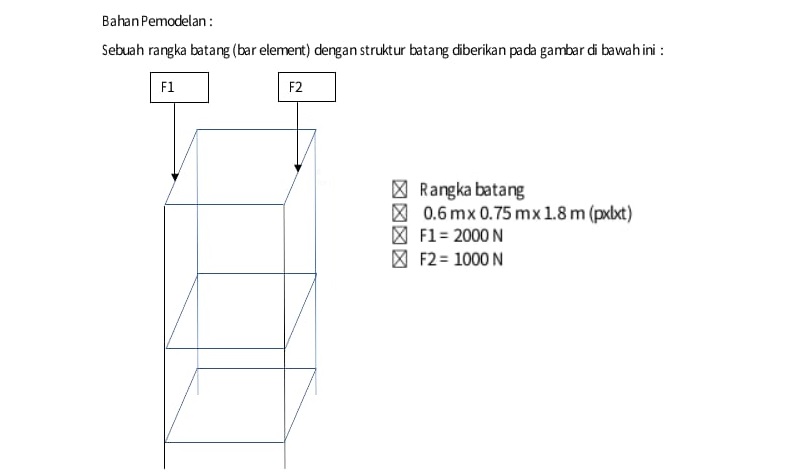
Geometri dan Load
Constraint:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi:
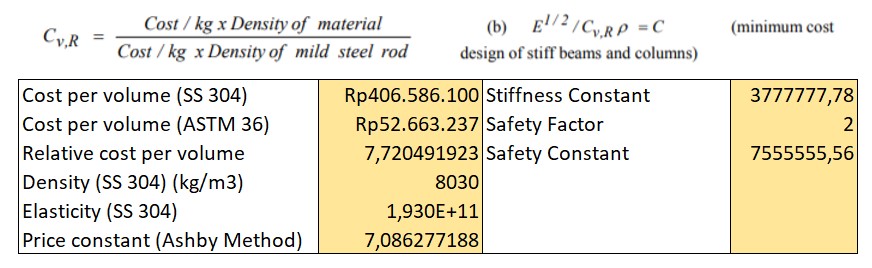
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
- Safety factor bernilai 2.
- Batas displacement 0,001 m sebelum buckling(pada kolom paling atas)
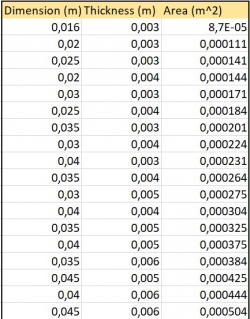
Koleksi Data:
Using Trusses Model (Modellica):
Displacement limit=0,0005 m
Stiffness Constant (A*E) = 3777777,778
Total Length=15,3 m
Resources:
http://www.matweb.com/search/DataSheet.aspx?MatGUID=1748ca73d11e4353b2aa700bfb119dfb
http://www.matweb.com/search/datasheet.aspx?matguid=d1844977c5c8440cb9a3a967f8909c3a
https://mitarcahyaabadai.wordpress.com/daftar-harga-besi-siku-2018/
https://duniabahanbangunanbandung.blogspot.com/p/harga-besi-siku-stainless-steel.html
http://www.wermac.org/steel/dim_angle_eq.html
Latar Belakang Teori:
Resources:
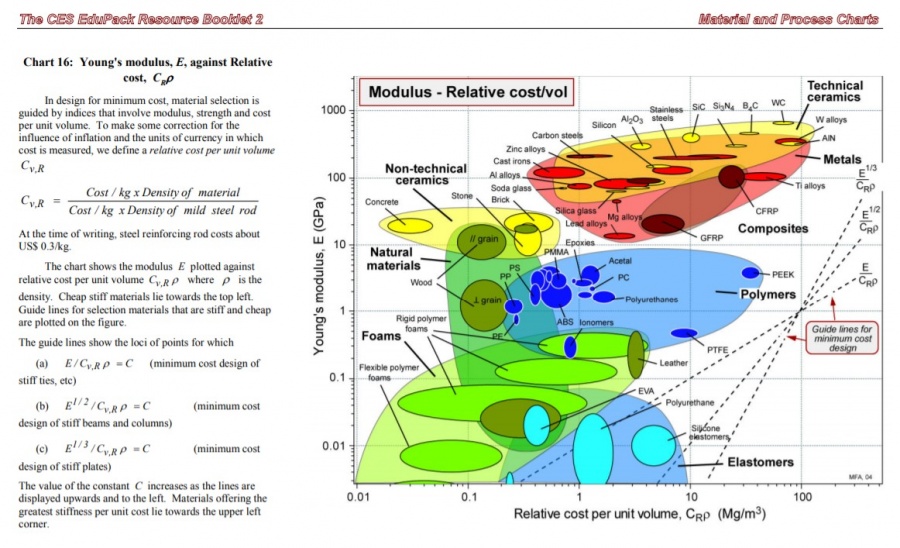
Ashby M, Materials selection in mechanical design, eds Reed Educ. & Prof. Pub. 1999.
Analisis Sementara:
Kode Modelica Pendukung:
|
Trusses Modelling model Trusses_3D_Tugas_Besar_Simplified2
//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=3777777.778; //Area
parameter Real Elas=1; //Elasticity (equals to one in order to determine the displacement limit)
//define connection
parameter Integer C[Trusses,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[Points,3]=[0.3,-0.375,0; //1
-0.3,-0.375,0; //2
-0.3,0.375,0; //3
0.3,0.375,0; //4
0.3,-0.375,0.6; //5
-0.3,-0.375,0.6; //6
-0.3,0.375,0.6; //7
0.3,0.375,0.6; //8
0.3,-0.375,1.2; //9
-0.3,-0.375,1.2; //10
-0.3,0.375,1.2; //11
0.3,0.375,1.2; //12
0.3,-0.375,1.8; //13
-0.3,-0.375,1.8; //14
-0.3,0.375,1.8; //15
0.3,0.375,1.8]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define boundary
parameter Integer b[:]={1,2,3,4};
//solution
Real displacement[N], reaction[N];
Real check[3];
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10;
Real ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
end Trusses_3D_Tugas_Besar_Simplified2;
|
Curve Fitting Function function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting; |