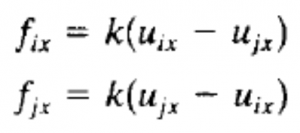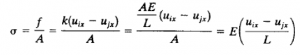Metnum03 - Gema Akbar Ilhamsyah
BIODATA DIRI
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Nama: Gema Akbar Ilhamsyah
NPM : 1806233386
Fakultas/Jurusan: Teknik/ Teknik Mesin
Tempat dan Tanggal lahir: Jakarta,7 Januari 2000
Contents
Pertemuan I
-Pemahaman Materi Sebelum UTS
Penjelasan Metode Numerik itu sendiri adalah teknik penyelesaian masalah dengan menggunakan operasi hitungan tambah, kurang, kali, bagi. Metode ini digunakan untuk membantu matematis untuk menyelesaikan permasalahan yang tidak dapat diselesaikan dengan metode analitik ataupun permasalahan yang sangat sulit dan memeakan banyak waktu untuk diselesaikan dengan metode analitik. Pada kesempatan kali ini saya akan mencoba menjabarkan apa saja materi mata kuliah yang dipelajari sebelum UTS, yaitu;
1. mencari akar akar persamaan non linear
Penyelesaian untuk mencari akar-akar persamaan non linear ada beberapa cara yaitu:
a)Metode Tertutup: Metode yang termasuk ke dalam golongan ini mencari akar di dalam selang [a,b]. Selang [a,b] sudah dipastikan berisi minimal satu buah akar, karena itu metode jenis ini selalu berhasil menemukan akar. Dengan kata lain, lelarannya selalu konvergen (menuju) ke akar, karena itu metode tertutup kadang-kadang dinamakan juga metode konvergen. b)Metode Terbuka: Yang diperlukan pada metode ini, adalah tebakan awal akar, lalu dengan prosedur lelaran, kita menggunakannya untuk menghitung hampiran akar yang baru. Pada setiap lelaran, hampiran akar lama yang dipakai untuk menghitung hampiran akar yang baru. Mungkin saja hampiran akar yang baru mendekati akar sejati (konvergen), atau mungkin menjauhinya (divergen). Karena itu, metode terbuka tidak selalu berhasil menemukan akar, kadang-kadang konvergen, kadangkala ia divergen.
2. turunan numerik
Untuk Penurunan Numerik, terdapat 3 metode, yaitu:
a)Forward difference aproximation
b)Backward difference aproximation
c)Central difference aproximation
3. regresi
Regresi merupakan alat ukur yg digunakan untuk mengetahui ada tidaknya korelasi antarvariabel. Analisis regresi lebih akurat dlm analisis korelasi karena tingkat perubahan suatu variabel terhdp variabel lainnya dpt ditentukan). Jadi pada regresi, peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula.
Regresi linier adalah regresi yang variabel bebasnya (variabel X) berpangkat paling tinggi satu. Utk regresi sederhana, yaitu regresi linier yg hanya melibatkan dua variabel (variabel X dan Y).
Y=a+bX
4. interpolasi
Pertemuan II
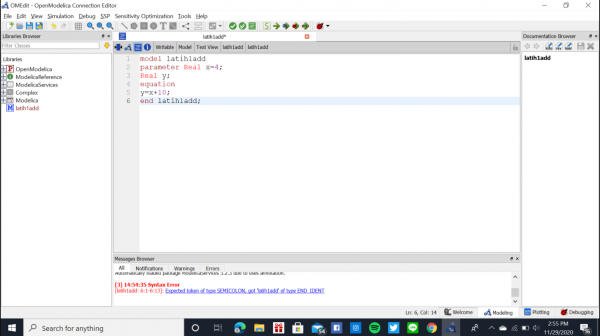
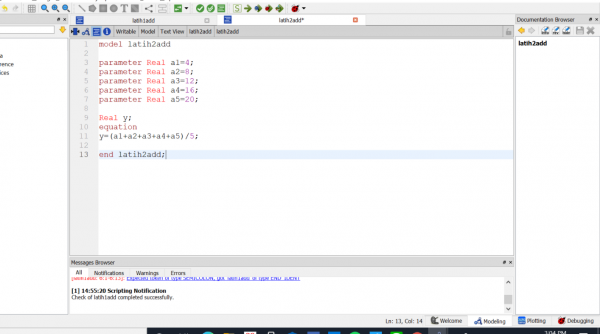
Pada pertemuan kali ini kami melakukan diskusi tentang software OpenModelica dengan Pak Dai. Lalu kami diberikan latihan untuk membuat perhitungan sederhana dengan software Open Modelica, yaitu menjumlahkan angka 10 dengan suatu variabel serta mencari rata-rata data yang didapat.
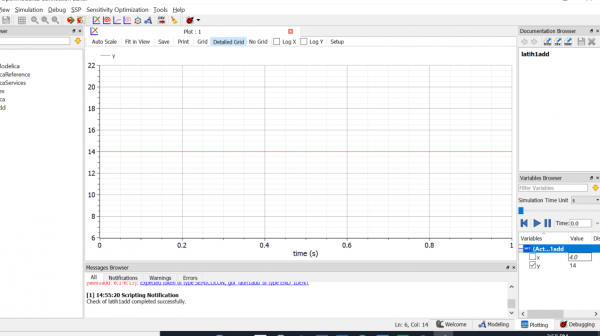
Saya Melakukan Perhitungan rumus y=x+10 dengan x=4
dan saya mendapat y=14
Tugas 2 = Penyelesaian persamaan aljabar simultan
Aljabar Simultan adalah suatu penyelesaian matematik yang kompleks sehingga membutuhkan penyederhanaan dengan menggunakan bantuan software yang sudah disediakan seperti OpenModelica. Ada beberapa metode yang bisa digunakan pada Aljabar Simultan:
1. Metode Eliminasi Gauss
2. Metode Crammer
3. Metode Gauss Seidel
4. Metode Gauss-Jordan
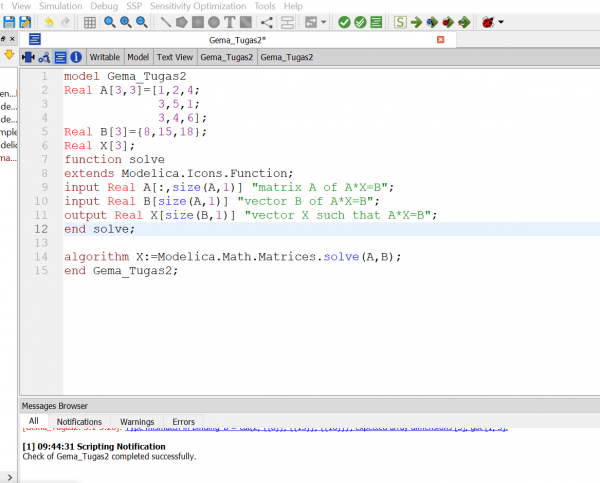
Untuk tugas 2 ini saya menggunakan persamaan berikut:
1. X1+2X2+4X3=12
2. 3X1+5X2+X3=15
3. 3X1+4X2+6X3=18
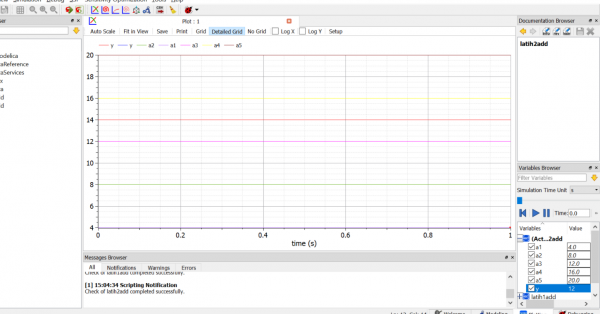
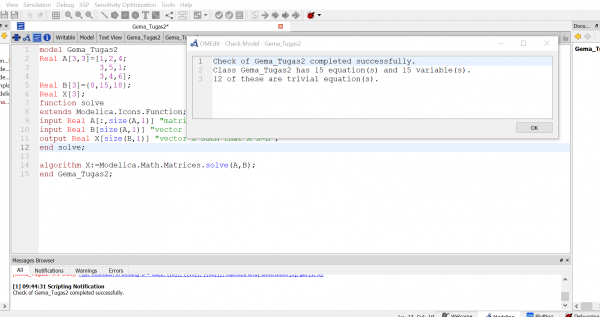
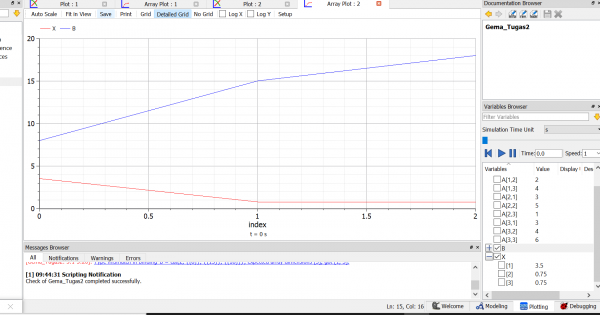
Lalu penyelesaian pada OpenModelica seperti berikut:
Saya mendapat penyelesaian persamaan diatas adalah: X1=3.5 , X2=0.75 , X3=0.75
Pertemuan III
Pada pertemuan 3 kali ini, kami berdiskusi dengan Pak Dai mengenai tugas 2 yang diberikan sebelumnya. Setelah itu Pak Dai menjelaskan langkah-langkah penyelesaian masalah dengan menggunakan Metode Numerik, yaitu:
1. Masalah Teknik 4. Model Numerik
2. Analisis Masalah 5. Komputer
3. Model matematis 6. Mendapatkan Solusi
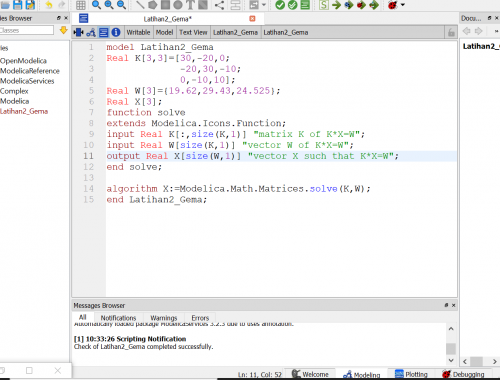
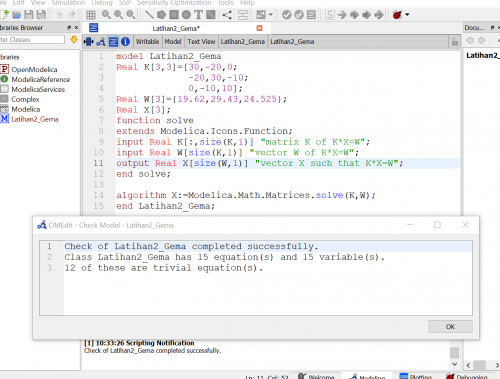
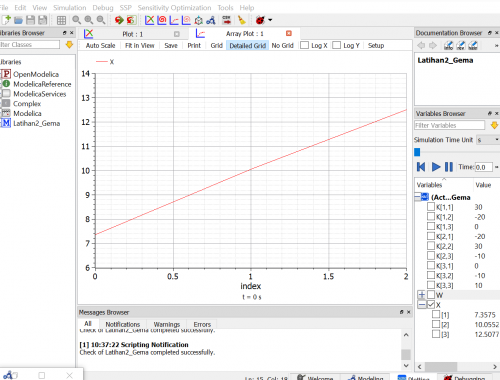
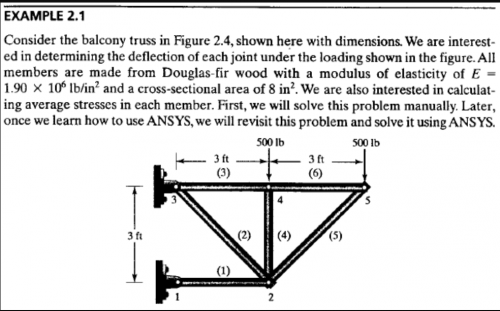
Setelah itu Pak Dai memberikan latihan studi kasus yang akan diselesaikan di OpenModelica. Kami diminta untuk menghitung gaya yang bekerja pada suatu benda dengan mengubah nya menjadi matrix 3x3 lalu mencari penyelesaian nya di OpenModelica, seperti dibawah ini:
Saya mendapat hasilnya, yaitu: X1=7.375 , X2=10.0552 , X3=12.5077
Tugas 3
Penyelesaian :
1. Mengubah problem menjadi node dan elemen
2. Konstanta kekakuan/stiffness constant
3. Persamaan elemen
4. Menggabungkan elemen
5. Menentukan kondisi batas dan beban
6. Pencarian solusi
- Menyelesaikan matriks:
-Nilai gaya reaksi
-Nilai Gaya Internal dan Normal Stress
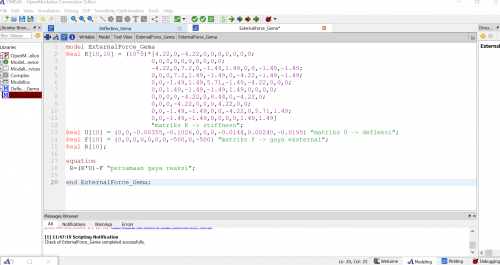
Dari persamaan diatas, diselesaikan dengan software OpenModelica seperti dibawah ini:
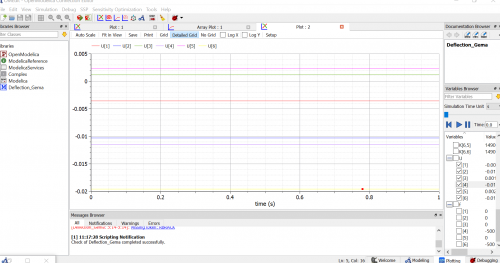
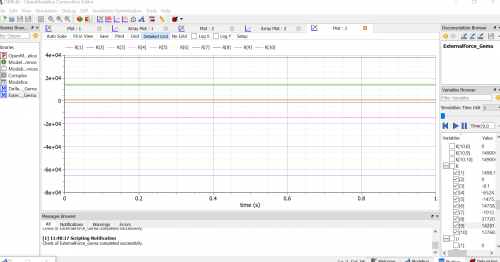
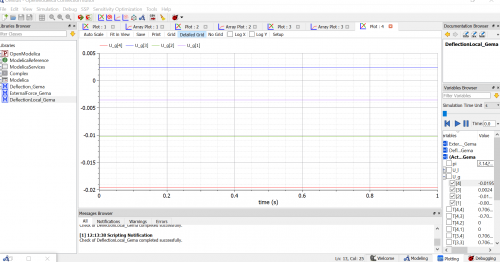
Hasil yang didapat adalah U2x=-0.0097 dan U6x=-0.012
Lalu hasil yang didapat dimasukan ke persamaan:
Dan didapat Internal force pada 5 elemen adalah 698lb
Untuk Normal Stress memakai rumus:
Dan Normal Stress pada 5 Elemen yang didapat sebesar 87lb/in^2
Pertemuan IV
Quiz
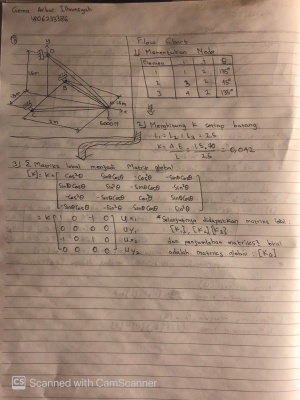
Flow Chart untuk penyelesaian soal:
Pertemuan V
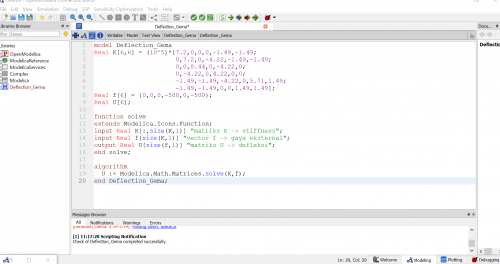
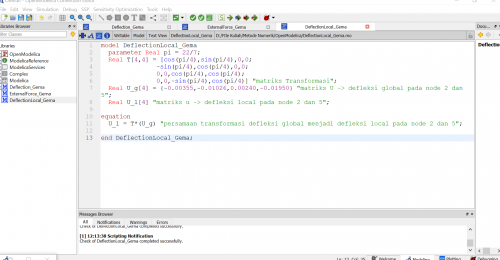
Pada pertemuan tanggal 7 Desember 2020, saya di ajarkan Pak Ahmad Indra Siswantara tentang quiz no 4 dan 8 yang dibantu oleh teman saya Ahmad Mohammad Fahmi yang telah menyelesaikan kedua nomor pada quiz sebelumnya, ada beberapa tahapan dari setelah kita membuat flow chart seperti gambar yang terlampir pada laman ini, yang pertama adalah solve striffness, lalu menentukan matriks pada setiap elemen dan dilanjutkan dengan pengintegrasian ke matriks global dan boundary condition yang nantinya akan mendapatkan variable U (Defleksi).
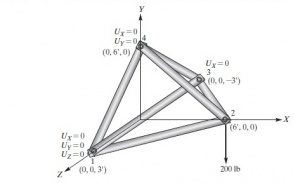
Seperti yang sudah dijelaskan Fahmi pada asistensi hari minggu, setelah memasukkan setup code dari node-node, soal no.4 menggunakan solving stifftring cos^theta, sin^2theta, dan sin theta * cos theta. Lalu pada no.8 menggunakan (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z). Setelah memasukkan matriks element, dikerjakan matriks global yang mencakup semua nilai pada matriks lokal. Setelah itu, function GaussJordan digunakan untuk mendapat variabel U, R, dan check force. Lalu, fuction dimasukkan ke dalam class kembali. Setelah check model, dapat dilakukan simulasi yang didapatkan nilai U dan R pada masing-masing simulasi. Lalu, saya diberikan tugas oleh pak Ahmad Indra Siswantara yaitu soal berikut ini
Pertemuan VI
Assalamualaikum Wr.Wb.
Pada pertemuan kali ini kelas kami mengadakan muhasabah individual untuk individual masing-masing. Pak Dai memberi kesempatan kami untuk bermuhasabah diri serta menilai diri sendiri mengenai kemampuan kami dengan range 0-100. Hasil muhasabah yang saya lakukan adalah saya menilai diri bahwa saya untuk kemampuan teori serta beberapa pemahaman konsep metode numerik sudah paham walaupun untuk pengaplikasian metode numerik itu sendiri dengan mata kuliah lainnya masih kurang. Untuk pengaplikasian metode numerik dengan coding atau open modelica, saya sendiri masih kurang memahami dan masih harus banyak latihan kembali.
Pertemuan VII
Assalamualaikum Wr.Wb.
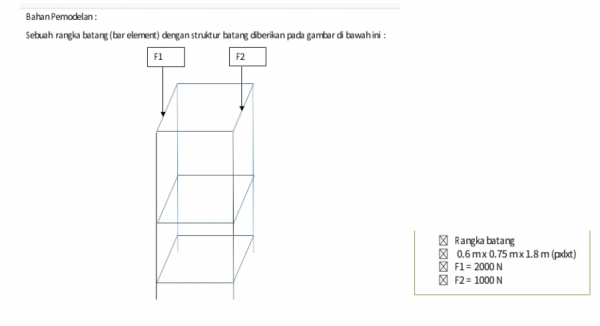
Tugas Besar
Diatas merupakan tugas besar yang diberikan di kelas Metnum 03. Kami disuru melakukan pemilihan material yang akan dipakai untuk membuat rangka serta kami harus melakukan optimasi untuk menentukan area yang optimal
Presedur pengerjaan tugas ini sendiri ada:
1. Menentukan asumsi dan constraint 2. Researh data profil besi siku 3. Permodelan Numerik 4. Komputasi 5. Optimasi 6. Penentuan akhir material
1. Menentukan asumsi dan Constraint
Asumsi yang digunakan adalah :
- Diasumsikan tidak ada bending karena bersifat truss - Beban terdistribusi pada node - Safety Factor = 2 - Batas displacement 0,001m sebelum terjadi buckling - Variabel bebas
Constraint yang ada adalah
1 Node 1,2,3,4 (lantai dasar) fixed 2 Beban F1 dan F2 terdistribusi ke node sekitaranya, sehingga: 3 Node 13 & 16 = 1000N 4 Node 14 & 15 = 500N
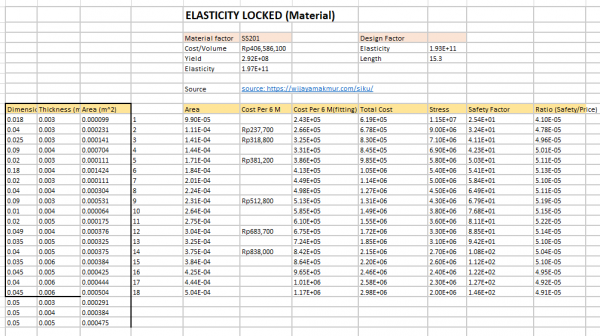
2.Researh data profil besi siku
Gambar tabel diatas merupakan data yang saya yang saya dapatkan dari hasil pencarian. material yang saya gunakan adalah SIKU SS201. material ini memiliki Yield Strenght sebesar 292 MPa dan Modulus Elastisitas sebesar 197 GPa.
3.Permodelan numerik - Coding dibawah ini merupakan coding yang saya gunakan untuk menghitung besar stress
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
parameter Real Area= (nilai area) ; //Luas Siku (Dimension=30x30x3mm)
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end TugasBesar;
- Ini merupakan permodelan untuk Curve Fitting
model callcurve
parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4};
parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));