Metnum03-Jenizhar Adivianto
KELAS METODE NUMERIK 03
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Contents
- 1 BIODATA DIRI
- 2 Pertemuan 1 : 9 November 2020
- 3 Pertemuan 2 : 16 November 2020
- 4 Pertemuan 3 : 23 November 2020
- 5 Tugas 3 Metode Numerik
- 6 Pertemuan 4 : 30 November 2020
- 7 Kuis Metode Numerik
- 8 Pertemuan 5 : 7 Desember 2020
- 9 Pertemuan 6 : 14 Desember 2020
- 10 Pertemuan 7 : 21 Desember 2020
- 11 TUGAS BESAR METODE NUMERIK
BIODATA DIRI
Nama : Jenizhar Adivianto
NPM : 1806181810
Program Studi : S1 Teknik Mesin Pararel
Pertemuan 1 : 9 November 2020
Assalamualaikum Wr. Wb
Selamat Pagi/Siang/Sore/Malam Semuanya
Pada pertemuan kali ini yaitu pertemuan pertama mata kuliah metode numerik oleh Pak Dai. Pak Dai memakai sarana belajar yang ia miliki yaitu wiki Air.eng.ui.ac.id ini. Pertama-tama Pak Dai memulai pembelajaran dengan menekankan 4 hal yang menjadi indikator pembelajaran pada saat kuliah. Yang pertama yaitu konsep. Kita harus memahami prinsip dan konsep terlebih dahulu sehingga bisa lebih leluasa dan tahu saat kapan harus dipakai. Yang kedua, kita harus mengetahui penerapan dan aplikasi dari teori dan konsep yang sudah kita pelajari. Yang ketiga, yaitu kita harus tahu kapan dan mengapa teori atau konsep tersebut kita pakai untuk menyelesaikan suatu permaslahan. Yang keempat yaitu penilaian diri sendiri. Dengan menilai diri sendiri, kita dapat mengetahui progress pembelajaran kita dan hal keempat ini merupakan hal yang harus dilakukan agar dapat melakukan hal 1 - 3.
di akhir pertemuan, Pak Dai memberikan kami tugas yaitu untuk menulis di air mengenai ilmu apa saja yang sudah kita dapatkan pada waktu sebelum uts dengan pak Engkos. Materi yang sudah di tulis di air.eng dibuatkan video mengenai penjelasannya kemudian di upload ke youtube. Yang terakhir yaitu mempelajari software modellica yang sudah didownload.
1. Hal yang sudah dipelajari
Pertama-tama, kami mempelajari bagaimana metode numerik secara garis besar. kemudian pada chapter 5, kami belajar mengenai beberapa metode-metode yang dipakai untuk menyelesaikan persamaan. Yang pertama itu ada bracketing method yang berisi graphical method, bisection method, dan False position method. Kemudian metode berikutnya ada open method yang berisi Fixed-point iteration, Newton Raphson method, Secant method, dan Brent's method.
Pada Chapter berikutnya, kami mempelajari tentang regresi linear. Disini, regresi linear biasa digunakan untuk membuktikan teori-teori yang sudah ada dengan eksperimen. Dengan mengambil sampel yang bervariasi, kami dapat menghitung beberapa variabel seperti error dan lain-lain. Metode ini sering dilakukan pada saat praktikum atau pada saat analisa setelah pengambilan data.
Materi terakhir sebelum uts yang kami pelajari adalah interpolasi. Interpolasi linier merupakan salah satu metode yang digunakan untuk mengetahui nilai dari suatu interval dua buah titik yang terletak dalam satu garis lurus. ada beberapa jenis yaitu newton Divided difference, Langrange, Spline, dan multidimensional.
2. Link Video Youtube
Berikut merupakan link dari video hasil progress pembelajaran saya mengenai openmodelica:
3. Hasil pembelajaran modellica
Untuk belajar modelica, pertama-tama saya membuka tutorial di youtube dengan link sebagai berikut : https://www.youtube.com/watch?v=SW5Eclf1tRs
Video tersebut berisi mengenai pengenalan modelica untuk pemula. Sebagian besar dari isi video tersebut masih menjelaskan tentang simbol-simbol, tools, interface, dan lain-lain. Pada libraries, terdapat berbagai macam tools yang dapat membantu kita dalam menggunakan modelica. Salah satunya adalah tools "modelica". di dalam tools tersebut, kita dapat menemukan banyak model-model yang dapat kita pakai nantinya seperti electrical, magnetic, mechanical, fluida, heat, dan lain -lain. dapat dilihat pada gambar di bawah ini
Pada video tersebut, ia menggunakan contoh controlled temperature pada heat transfer. Kita bisa melihat blok diagram, plot pemrograman diagram tersebut, dan teks dokumen yang menjelaskan diagram tersebut. Selanjutnya, ada tools berupa simulation. Kita perlu check model untuk memastikan bahwa model bisa dipakai. perlu dipastikan bahwa equation dan variabel sama. Bila tidak, maka terjadi masalah singularity. Setelah check model, maka kita bisa mensimulasikan model tersebut. Setelah simulasi selesai, dapat dilihat grafik-grafik dan variabel dimana kita bisa memilih apa yang ingin kita lihat pada sisi variabelnya.
Berikutnya ada simulation setup dimana disitu kita bisa mengatur start time, stop time, interval, metode, dan lain-lain. Pada simulation setup juga terdapat translation page, simulation page, output, dan archived simulation.
Untuk Tutorial pembuatan model, saya membukan tutorial di youtube dengan link sebagai berikut : https://www.youtube.com/watch?v=esSMzMCFwbo
Video ini menjelaskan tentang bagaimana kita membuat model baru. Pada video tersebut, digunakan contoh nyata heat transfer dan dijadikan model matematika terlebih dahulu. Pertama-tama buka tab modeling di pojok bawah kiri. kemudian klik new file dan pilih "package". Setelah itu, klik kanan pada heat transfer di library dan pilih new open modelica course. Pilih connector dan tulid "heatport" dan pilih partial. Buka text view bar pada bagian atas
Kemudian buka dua heat class baru dengan jenis connector dan nama "heatport_a" dan "heatport_b". Kita menggunakan dua heatport karena pada heatflux keadaan ini ada inlet dan outlet. Pada kedua class tersebut, buka text view dan tulis:
Setelah membuat heatpart, kita membuat model matematika pada class baru yang akan di hitung. Yaitu ada pada wall, ambient(lingkungan), dan convection. Dan setelah ketiga model tersebut sudah ditulis, kita menggabungkan semua dengan model cooling. jangan lupa setiap selesai membuat model pada text view, di check terlebih dahulu dengan klik tombol centang hijau. Nanti akan saya tunjukkan di video bagaimana cara mengisinya. kalau sudah, bisa coba ke simulation dan di setup stop time = 10s. sisanya default saja. Kalau sudah, run simulation. Setelah selesai, dapat dilihat plort dari persamaan yang sudah dibuat dengan grafik.
Terima kasih, sekian rangkuman pada pertemuan pertama
Wassalamualaikum Wr.wb.
Pertemuan 2 : 16 November 2020
Assalamualaikum Wr. Wb
Selamat Pagi/Siang/Sore/Malam Semuanya
Pada kelas hari ini Pak DAI menanyakan bagaimana progress tugas kami mengenai progress pembelajaran open modelica itu sendiri. Kemudian Pak DAI memberikan kami 2 latihan soal yaitu:
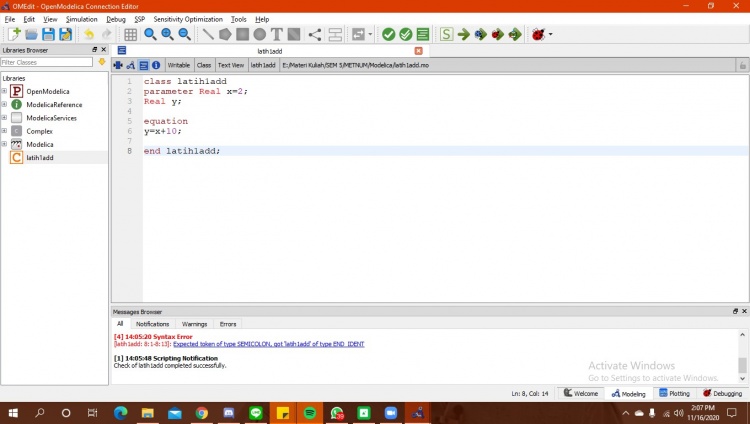
1. buatlah modeling mengenai persamaan y = x + 10
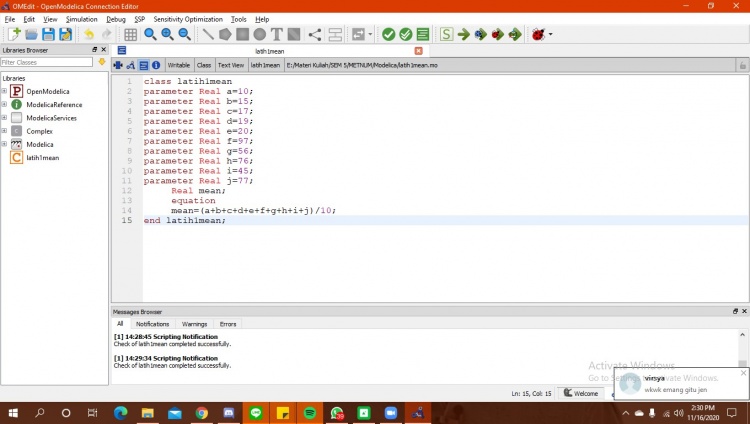
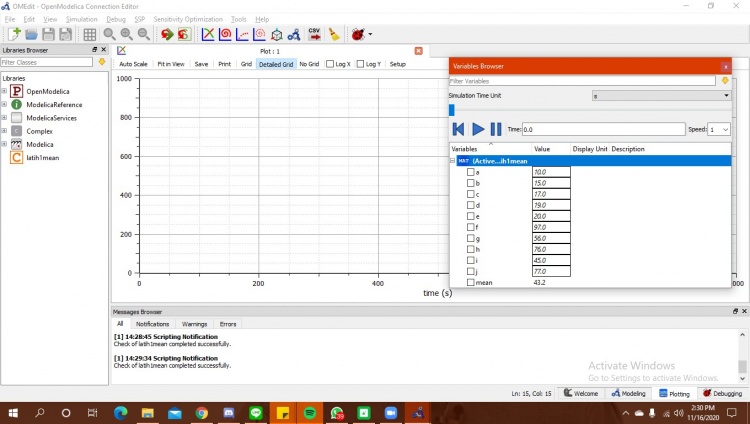
2. buatlah modeling mengenai mean (rata-rata)
Setelah itu, Pak Dai memberikan tugas yaitu membua suatu program untuk menyelesaikan persamaan aljabar dengan gauss elimination.
Bentuk umum sistem persamaan linear mempunyai matriks yang bersesuaian yang disebut matriks yang diperluas atau augmented matrix. Pada mata kuliah sebelumnya kita mengerjakan persamaan dengan manual. Namun, pada mata kuliah metode numerik ini, kita dapat menyelesaikan persamaan-persamaan tersebut dengan program yang kita buat sendiri.
Saya menggunakan persamaan yaitu :
a + 2b + 3c + d = 9
3a + 5b + 7c + 4d = 12
4a + b + c + 3d = 23
6a + 7b + 5c + 2d = 0
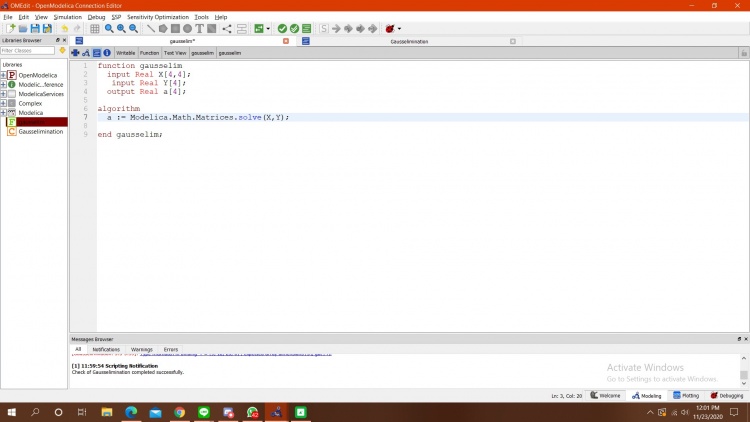
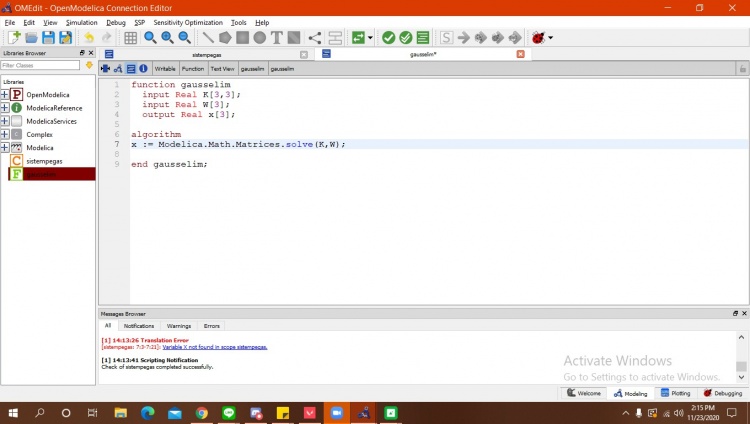
saya menggunakan program koding pada open modelica pertama dengan membuat function terlebih dahulu yaitu sebagai berikut :
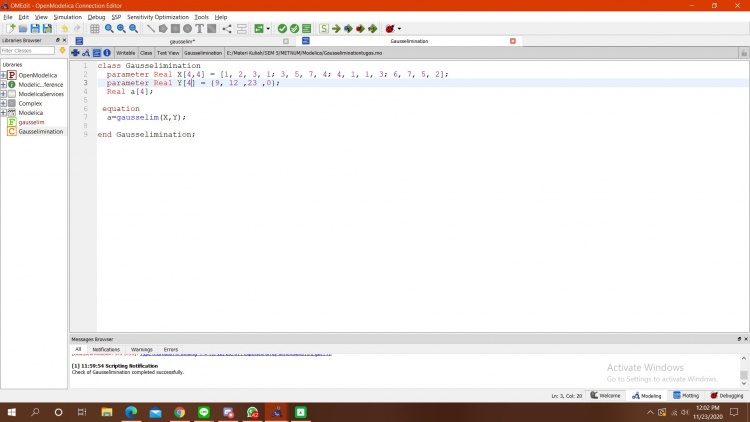
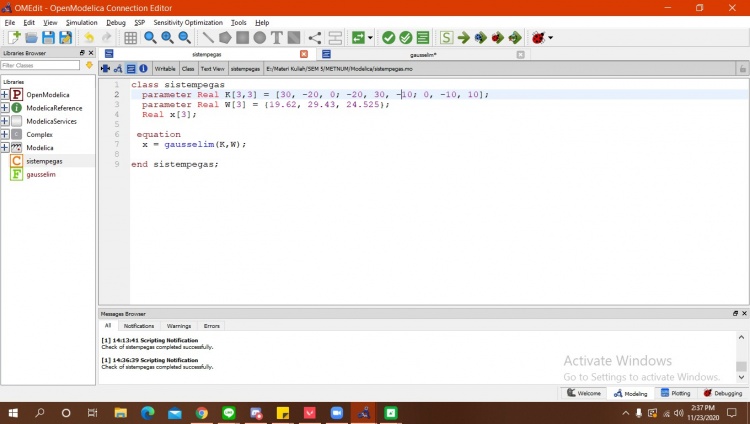
setelah itu, saya memasukkan data - data angka yang sudah diketahui kedalam class dan menyambungkan fungsi yang pertama ke dalam equation pada class seperti berikut :
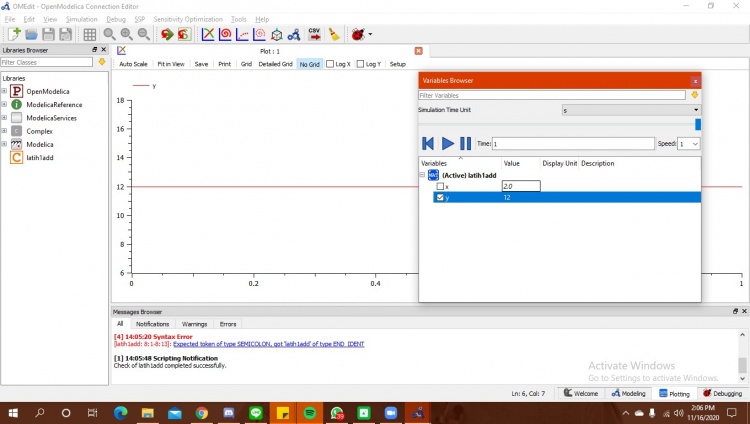
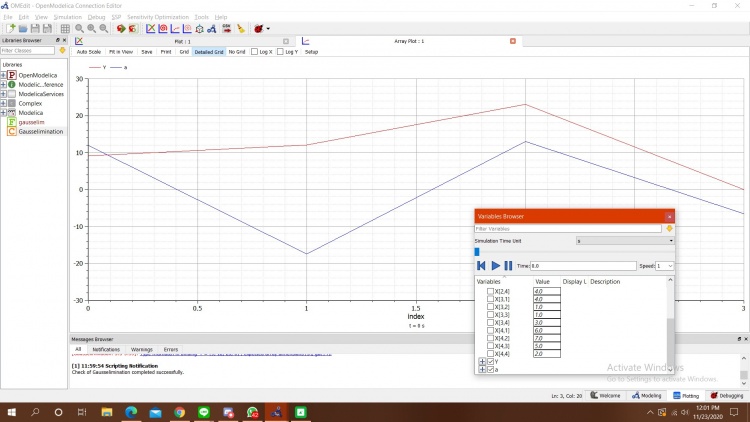
Bila sudah, pastikan di cek terlebih dahulu pada centang hijau. Kemudian, apabila sudah benar, langsung kita simulasikan. Berikut merupakan hasil dari simulasi saya :
Terima Kasih
Wassalamualaikum Wr. Wb
Pertemuan 3 : 23 November 2020
Assalamualaikum wr. wb.
Pada hari ini, pak Dai menghimbau kami untuk membaca materi mengenai permodelan pegas di buku metode numerik terlebih dahulu. Kemudian, pak Dai menjelaskan bagaimana cara mengaplikasikan metode numerik ke permodelan teknik.
Masalah teknik -> analisis teknik -> model matematis -> model numerik -> komputer -> solusi
Kemudian pak dai menjelaskan bagaimana permodelan aplikasi pegas. pertama dari masalah tekniknya yaitu merupakan sistem pegas. kemudian pada analisis teknik kita menentukan hal-hal apa saja yang kita ketahui dalam persamaan tersebut. kemudian dengan hukum hooke kita membuat model matematisnya. Selanjutnya dengan openmodelica kita dapat membuat model numerik dan perhitungan simulasi komputernya untuk mendapatkan solusi
Selanjutnya, pak Dai menghimbau kami untuk membuktikan matriks sistem pegas yang ada di buku dengan perhitungan pada openmodelica. Pada kali ini saya menggunakan fungsi gauss elimination karena hal yang ingin kita buktikan berbentuk matriks. kemudian saya menggunakan class untuk menginput data-data matriks yang sudah ada sehingga dapat kita hitung otomatis nantinya dengan program yang sudah kita buat. koding dari saya yaitu dapat dilihat dibawah ini:
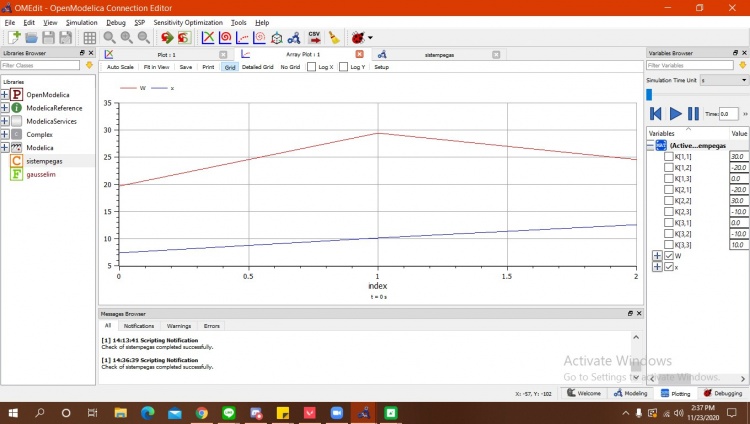
Berikutnya merupakan grafik yang didapat dari hasil simulasi. Disini dapat dilihat bahwa grafik W disini sesuai dengan apa yang ada dibuku. Berarti perhitungan sudah sesuai dan x disini yang merupakan perpindahan berarti sudah terbukti benar. Grafik tersebut dapat dilihat dibawah ini
Terima kasih
Wassalamualaikum Wr. Wb.
Tugas 3 Metode Numerik
Assalamualaikum wr wb.
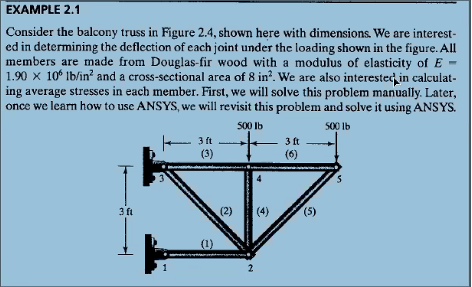
Pada kali ini saya akan mengerjakan tugas yang diberikan oleh pak Dai yaitu soal dibawah ini
Setelah membaca soal, kami dihimbau untuk membuat model matematika pada open modelica. kodingannya dapat dilihat dibawah ini :
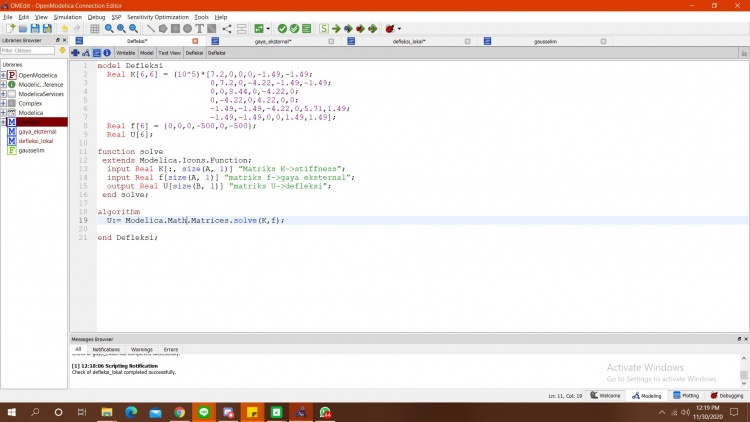
1. Pencarian Defleksi
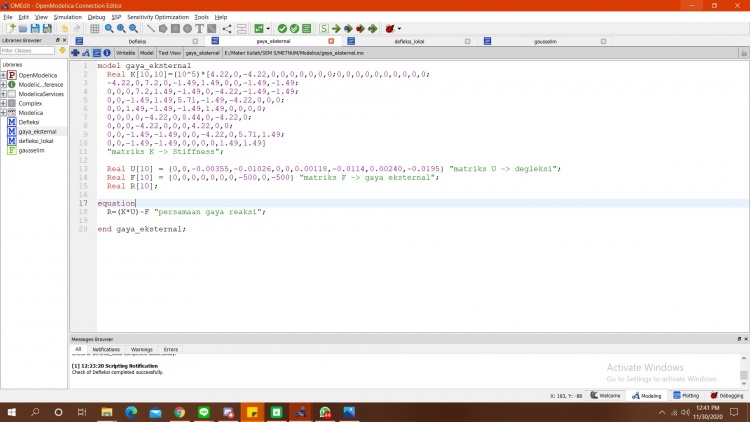
2. Pencarian Gaya Eksternal
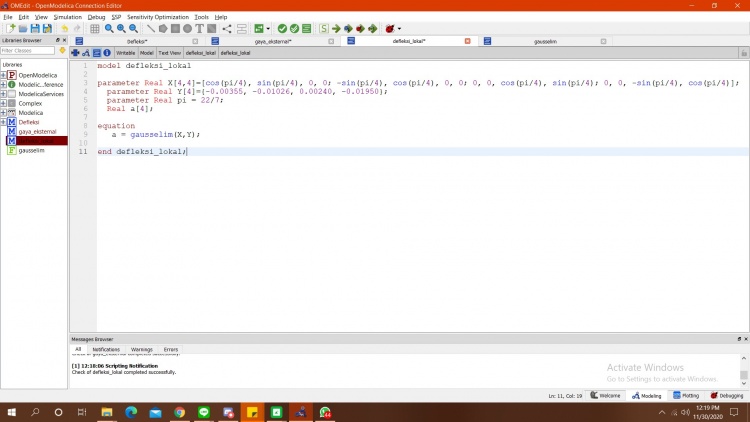
3. Pencarian Defleksi lokal
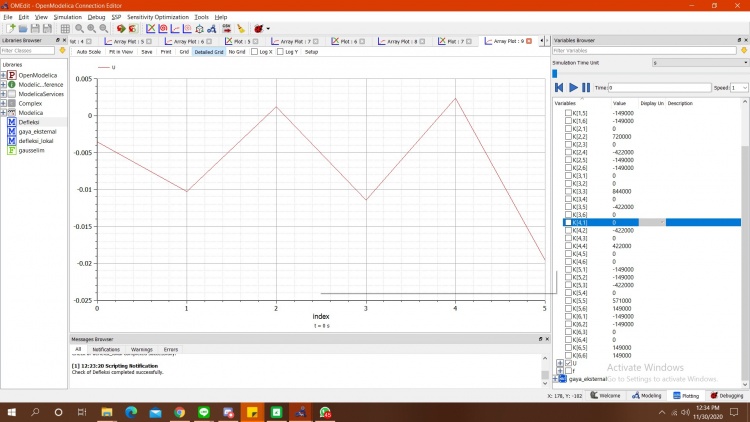
berikut merupakan hasil simulasi
1. Simulasi defleksi
2. Simulasi Gaya Eksternal
3. Simulasi Defleksi lokal
Sekian tugas saya
Terima kasih
Wassalamualaikum Wr. Wb.
Pertemuan 4 : 30 November 2020
Assalamualaikum wr. wb.
pada hari ini pertemuan dibuka oleh Pak Dai, beliau mengingatkan kembali kepada kita bahwa metnum ini merupakan gabungan antara matematika dan fisika dengan tugas yang diberikan minggu lalu. Kemudian, Pak Dai memberikan pertanyaan mengenai perbedaan statik dan dinamik. Perbedaannya adalah kalau statik bebannya tidak berubah terhadap waktu sedangkan berubah pada dinamik.
Kemudian pak Dai menghimbau kami untuk melihat kodingan dari saudara christoper untuk mempratikkannya dalam open modelica itu sendiri. kode - kode nya addalah sebagai berikut:
function GaussJordan
// Gauss-Jordan Algorithm // Transforms input matrix A into reduced row echelon form matrix B // Christopher S.E. November 2020
input Real [:,:] A; // An augmented matrix of m*n output Real [:,:] B; // Output matrix in reduced row echelon form
// Local variables protected Integer h = 1; // Initialize pivot row Integer k = 1; // Initialize pivot column Integer m = size(A,1); // Number of rows in matrix Integer n = size(A,2); // Number of columns in matrix Integer c = 0; // Index counter Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column; // Vector containing pivot column data Real [:] pivot_row; // Vector containing backwards pivot row data Real [:,:] temp_array; // Stores matrix data when switching rows Real r; // Ratio value used for row operations
// Limit to handle floating point errors Real float_error = 10e-10;
algorithm
// Transfer input matrix A into variable B B := A;
while h <= m and k <= n loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_column := {B[i,h] for i in h:m};
// Get position index of lowest row with greatest pivot number
c:= h-1;
for element in pivot_column loop
c := c+1;
if abs(element) == max(abs(pivot_column)) then
max_row := c;
end if;
end for;
// No pivot in this column, move on to next column
if B[max_row, k] == 0 then
k := k+1;
else
// Swap Rows h <-> max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
// Divide pivot row by pivot number
B[h] := B[h]/B[h,k];
// For all rows below the pivot
for i in (h+1):m loop
// Store the ratio of the row to the pivot
r := B[i,k] / B[h,k];
// Set lower part of pivot column to zero
B[i,k] := 0;
// Operations on the remaining row elements
for j in (k+1):n loop
B[i,j] := B[i,j] - B[h,j] * r;
end for;
end for;
// Move on to next pivot row and column
h := h+1;
k := k+1;
end if;
end while;
// The matrix is now in row echelon form
// Set values of (h,k) to (m,n) h := m; k := n;
while h >= 1 and k >=1 loop
// Dealing with floating point errors
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
// Finding the pivot
pivot_row := {B[h,i] for i in 1:k};
// Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k := c;
// No pivot in this row, move on to next row
if B[h, k] == 0 then
h := h-1;
else
// Perform row operations
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] * r;
end for;
// Move on to next pivot row and column
h := h-1;
k := k-1;
end if;
end while;
// The matrix is now in reduced row echelon form
end GaussJordan;
Kuis Metode Numerik
Assalamualaikum wr. wb.
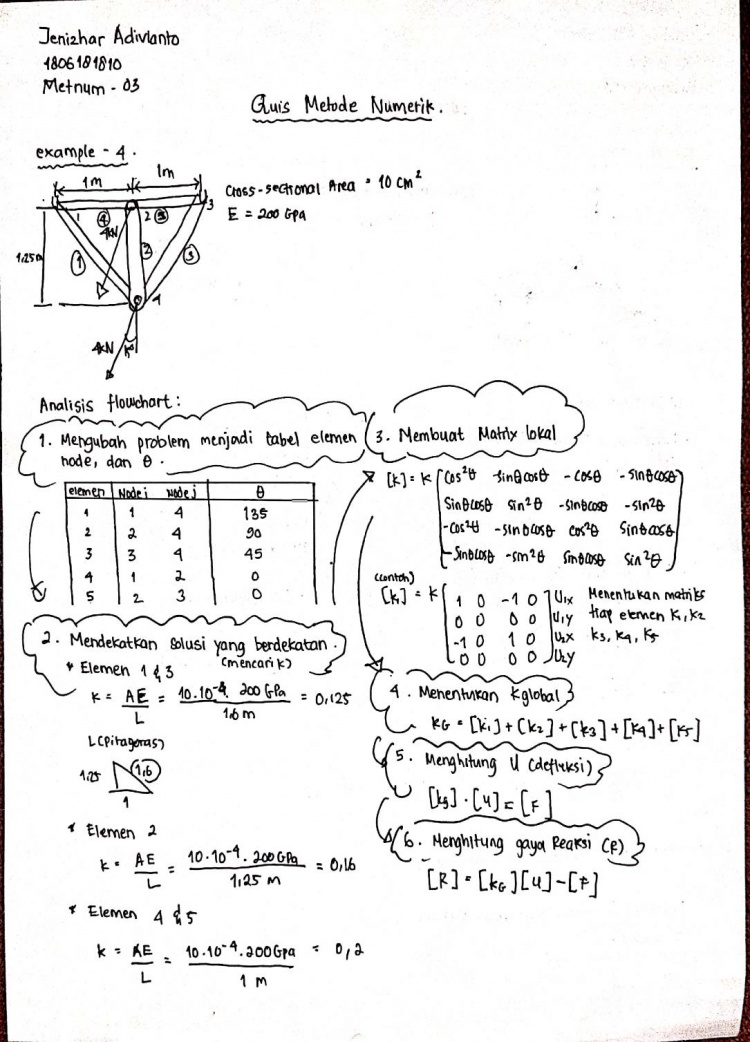
berikut merupakan flow chart dari kuis yang sudah diberikan yaitu example 4 dan example 8.
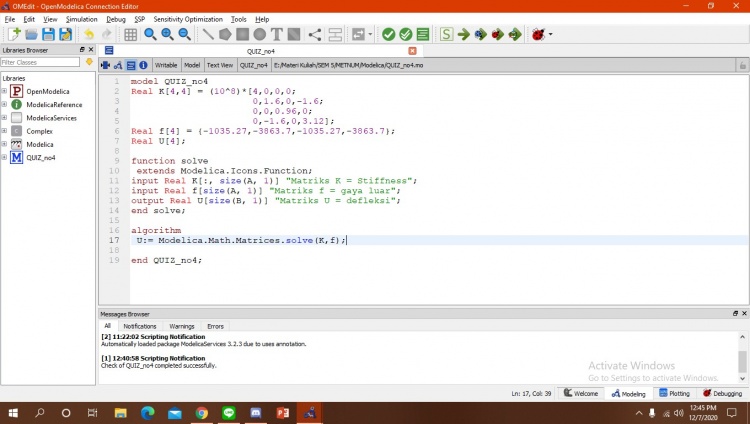
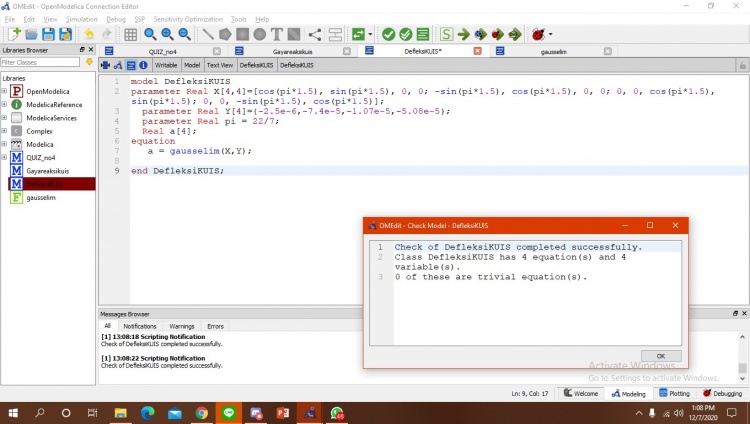
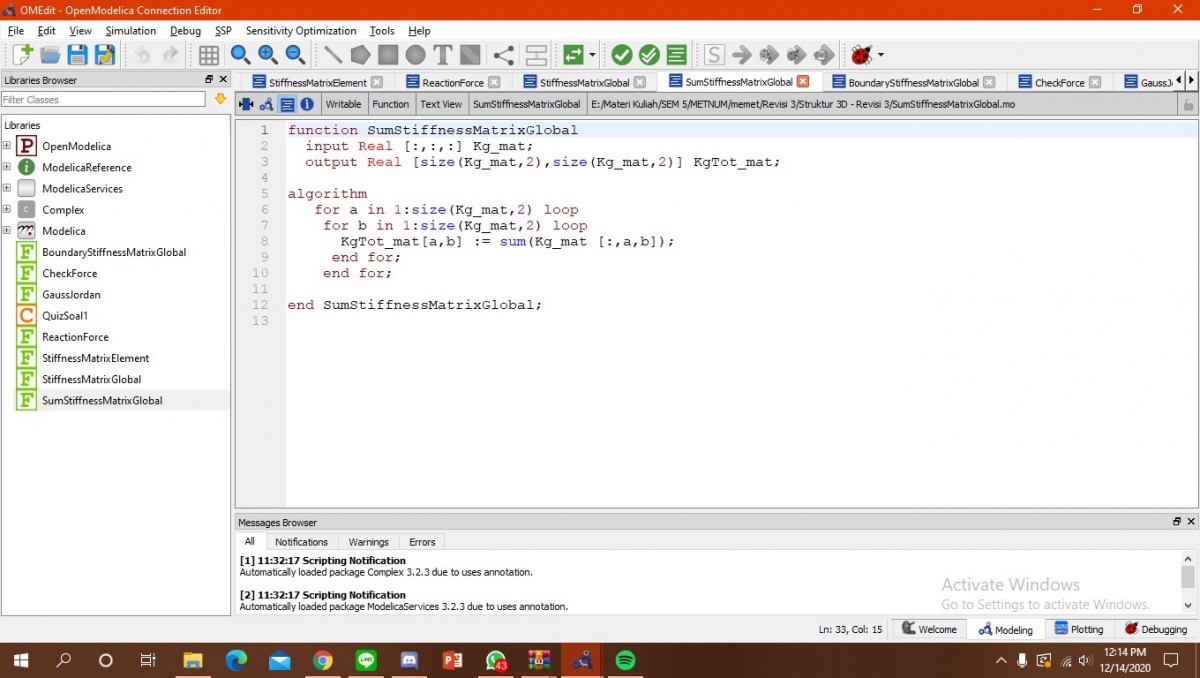
Pada soal nomor 4 kita pertama-tama harus menentukan node - node dari elemen yang ada pada soal dan juga sudut teta. Variabel node tersebut memiliki variabel i dan j. Diketahui juga dalam soal yaitu luas permukaan (A) = 10^-3m2 lalu modulus elastisitas (E) = 200GPa. Diketahui juga panjang batang yaitu 1m, 1,25m, dan 1,6m. Untuk melakukan simulasi di open modelica, kita harus menentukan matriks lokal terlebih dahulu yang nantinya ditambahkan untuk menentukan matriks global. Matriks global inilah yang nantinya kita bisa masukkan ke open modelica sebagai parameter real. Kode program dari open modellica yang saya buat adalah sebagai berikut:
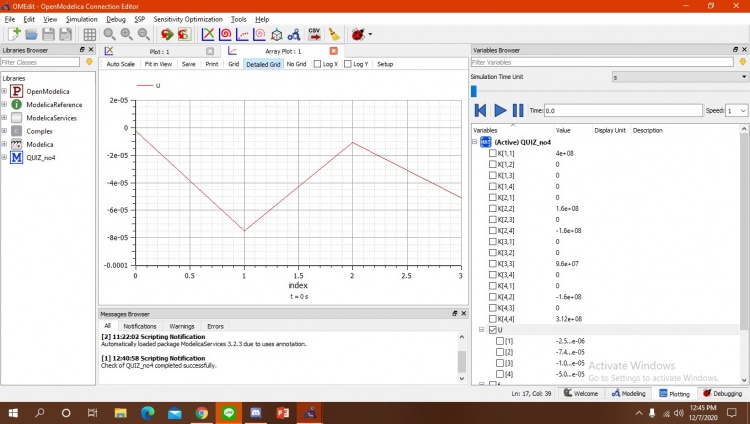
Karena pada 1 dan 3 batang fix dan tidak ada gaya luar, maka matriks kita hilangkan baris dan kolom 1, 2, 5, 6. Setelah saya cek model sudah benar memiliki 24 equation dan 24 variabel
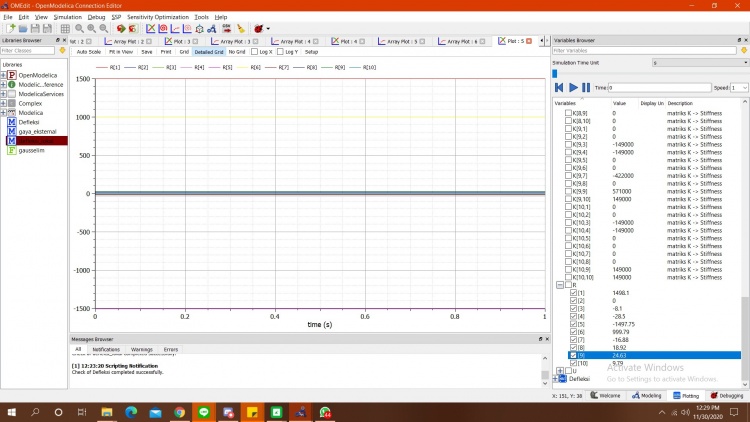
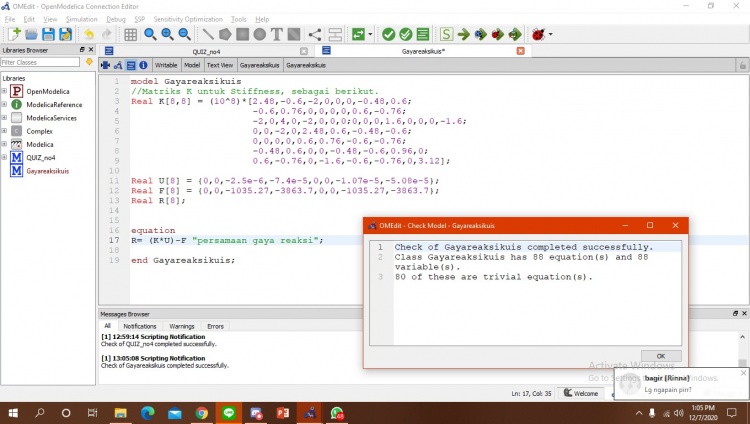
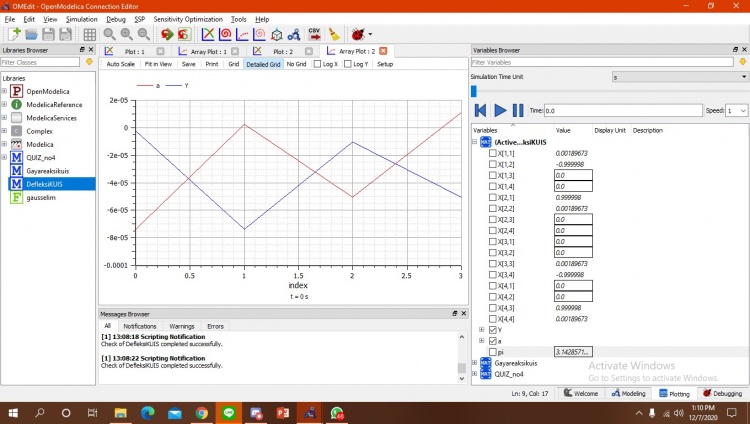
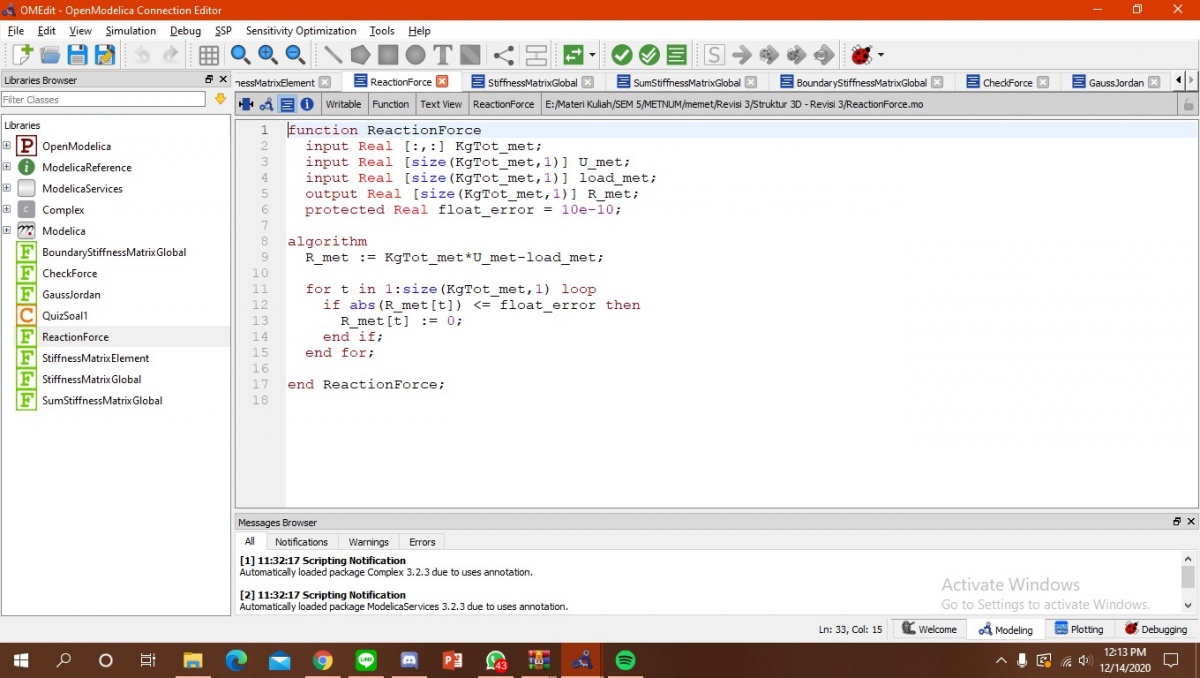
setelah disimulasikan berikut diatas merupakan grafik dari U. Tahap selanjutnya adalah menghitung gaya reaksi dari trusses dengan rumus R=(K*U)-F. U sudah diketahui diperhitungan sebelumnya dan K F sudah diketahui pada soal. berikut merupakan kodingan dari perhitungan.
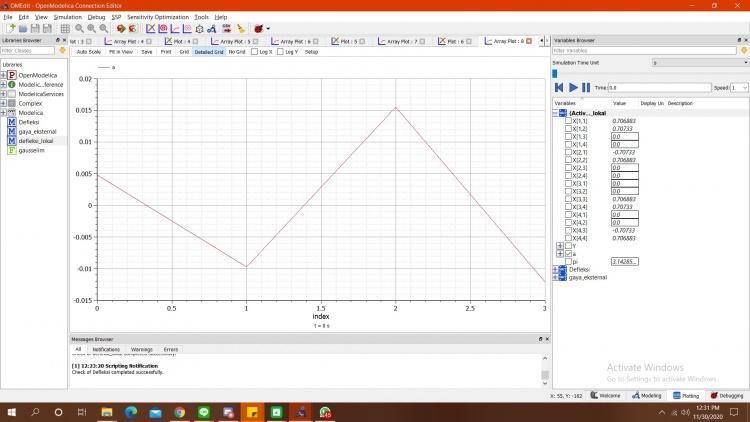
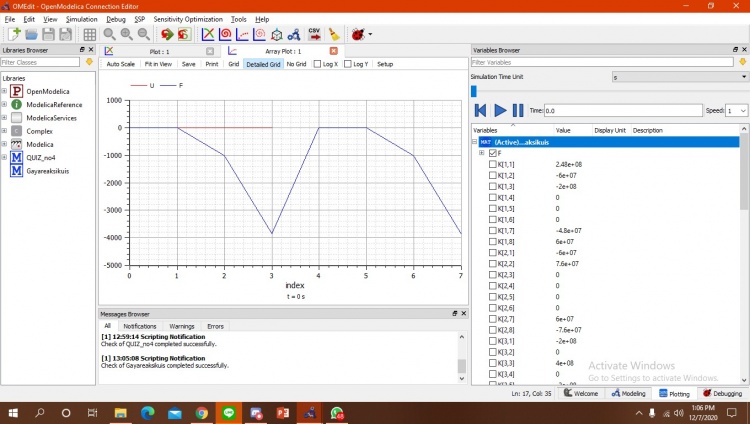
Berikut merupakan kodingan untuk perhitungan defleksi dan hasiil grafiknya
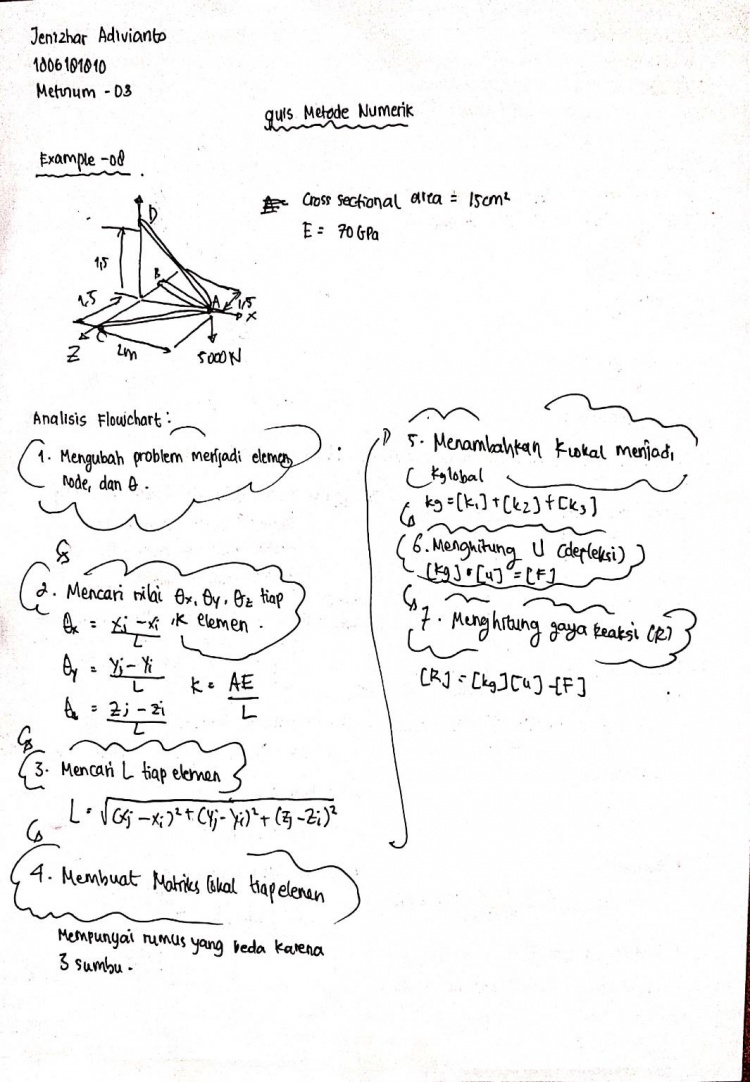
Untuk Soal no 8
Terima kasih
Wassalamualaikum wr. wb.
Pertemuan 5 : 7 Desember 2020
Assalamualaikum wr.wb
pada hari ini kelas dibuka oleh pak Dai dengan memanggil saudara Edward Josua untuk membantu menjelaskan tahap-tahap dalam menyelesaikan soal-soal.
kemudian saudara ahmad menjelaskan mengenai flowchart yang ia buat sendiri walaupun belum mengaplikasikan hitung-hitungannnya, tetapi ahmad menjelaskan mengenai tahapan untuk menyelesaikan soal. Pertama solve stiffness, kemudian buat matrix global dari setiap elemen, selanjutnya adalah menyelesaikan matriks global dan mengimplementasikan boundary condition, kemudian didapatkan U.
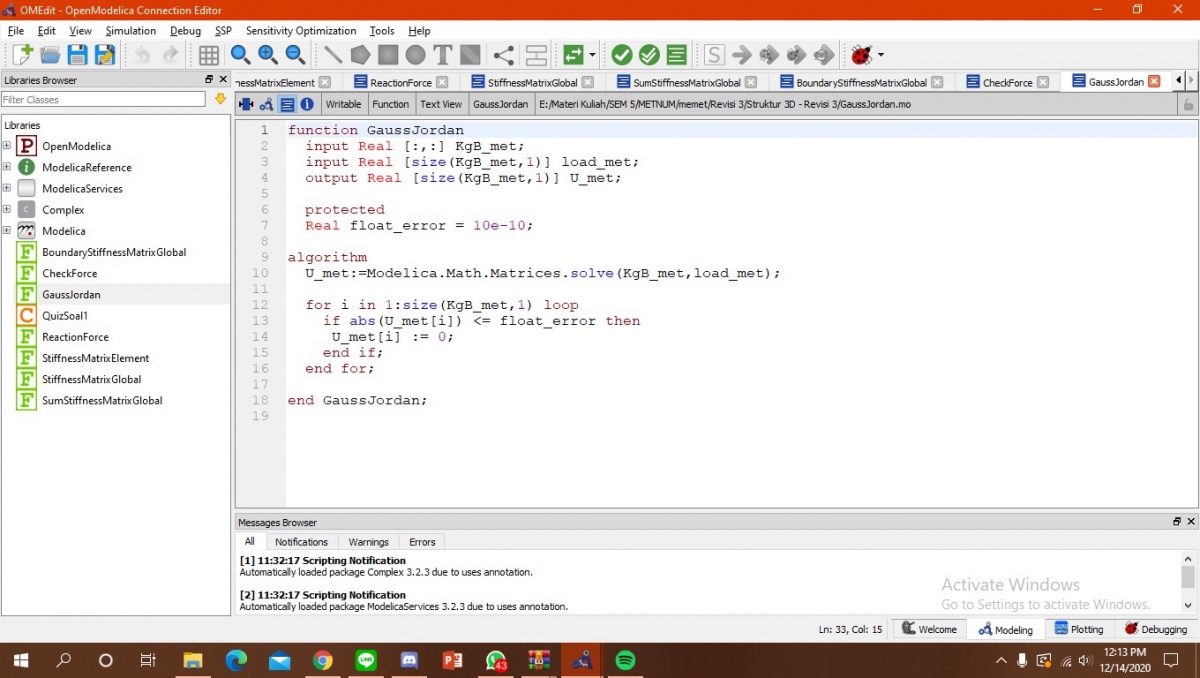
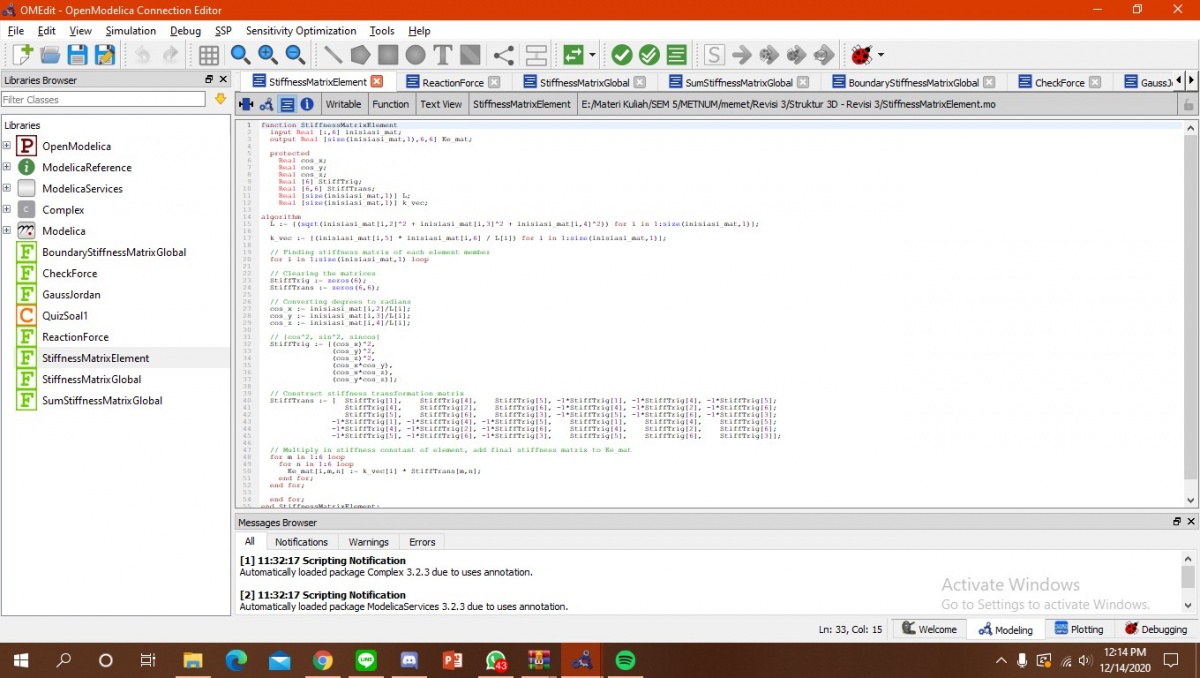
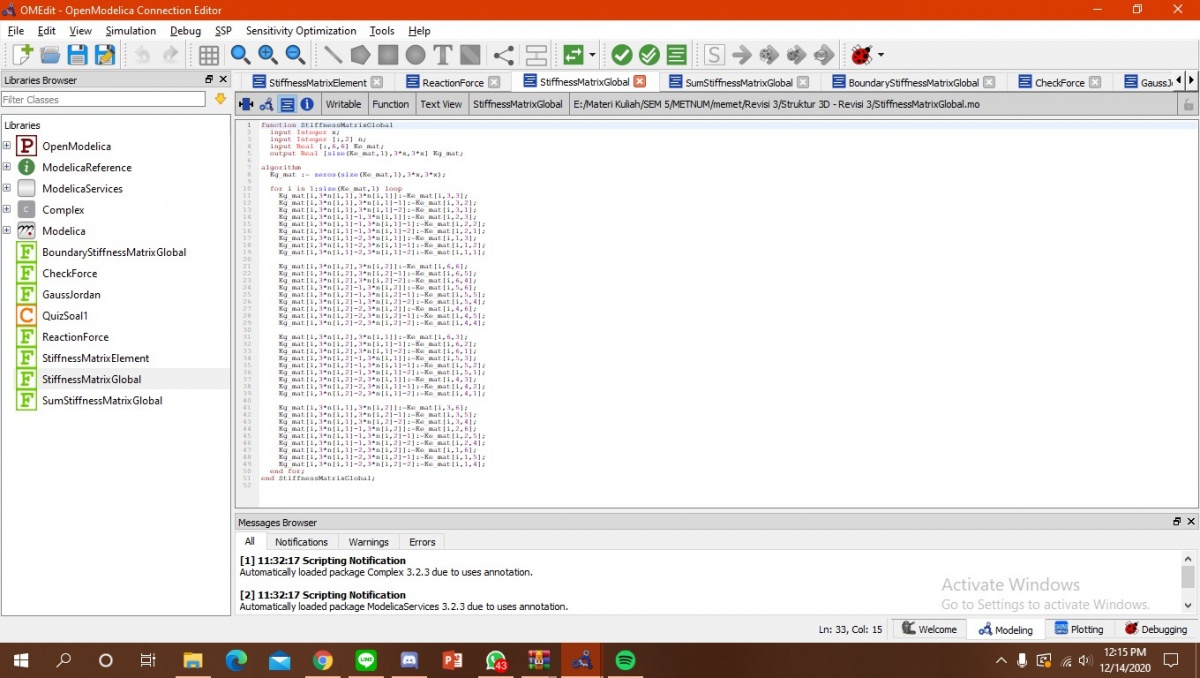
Pada Stiffness matrix elemen, ada float error karena perhitungan dalam radian. untuk Stiffness matrix global kita menentukan matrix global. Selanjutnya kita mengeliminasi menggunakan gauss jordan matrix global tersebut dan kita harus juga menghilangkan floating error. Terakhir yaitu masukkan rumus R=(K*U)-F
1. Pembelajaran Koding Fahmi
Kemudian pak Dai memberikan kami tugas mengenai pembahasan oleh saudara Ahmad Muhammad Fahmi tentang kodingan yang dibuat olehnya mengenai kuis nomer 4 dan 8. Untuk membantu pembelajaran kami, Fahmi memberikan video rekaman tutorial yang berisi diskusi pada link dibawah ini :
https://drive.google.com/file/d/1n0zvwmn-3G4DWYCSPD48-Xfrp9_kT3R0/view?usp=sharing
Pertama-tama, untuk mengerjakan nomer 4 yang 2d, Fahmi membuat beberapa function yang nanti akan digunakan dan 1 class untuk membuat penyelesaian atas soal yang diberikan. Pada class, Saudara ahmad memasukkan parameter REAL (inisiasi) yang berisi element, theta, A, E, L. Kemudian kita menginput node - node yang ada dengan memasukkan matriks dengan parameter integer. mengapa memakai integer? karena integer adalah bilangan bulat sedangkan kalau real bisa berbentuk desimal atau pecahan. Pada parameter integer kita memanggil matriks inisiasi pada kolom satu untuk di sesuaikan dengan node-node yang bersangkutan. Kemudian kita meng-input jumlah node yaitu n=4 dan Boundaries pada node. Boundaries pada node ini yaitu pada titik 1 dan 3 karena mereka merupakan tumpuan. Setelah itu, kita memasukkan load dengan menginput parameter real (2*n). Kita mengalikan n dengan 2 karena disini gaya ada 2 arah yaitu x dan y. Sesudah mengisi load, kita menginput equation dengan fungsi-fungsi yang sudah dibuat juga pada function oleh Fahmi. Kodingan dari Fahmi dapat dilihat pada file yang sudah dikirim di WA.
Untuk pembahasan dari function, pertama-tama kita melihat terlebih dahulu dari function stiffnessmatrixelement. Disini kita menginput terlebih dahulu input yaitu matriks inisiasi (:,5) dan outputnya adalah matriks dari Ke yang tadi ada pada equation pada class. Kita bisa memasuki parameter tanpa harus menulis ulang pada function dengan memanggil parameter pada Class. Dengan menggunakan protected maka parameter dapat dipanggil. Parameter yang kita ambil untuk Ke adalah Theta, StiffTrig, Stifftrans, k_vec, dan Floating error. Untuk function-function yang lainnya juga bisa dilihat pada file yang sudah diberikan di WA.
Untuk Soal 3d, terdapat perbedaan kodingan pada boundaries dari node-node yang diberikan. Terdapat perbedaan juga pada matrix parameter real karena data yang ada pada element, theta, A, E, L juga berbeda. Kita tetap menggunakan function yang sama.Jadi intinya adalah kita menggunakan pemrograman yang sama, namun hanya data-data saja yang berbeda sehingga kita harus menyesuaikan kembali dengan apa yang ada pada soal
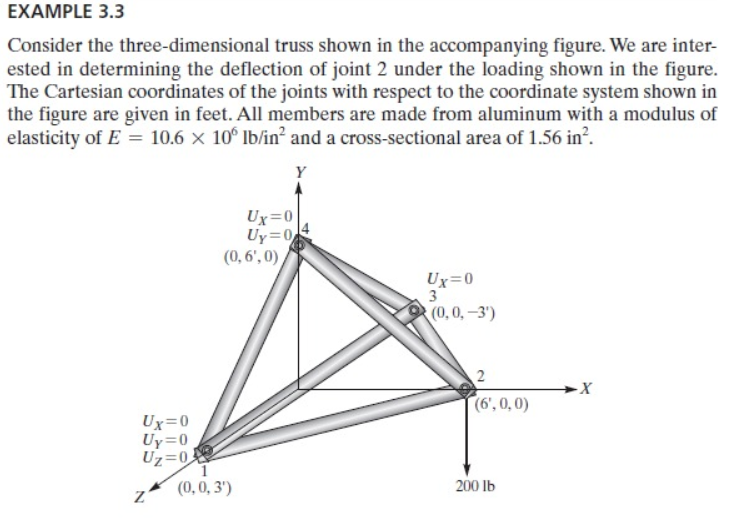
2. Aplikasi pada example 3.3
Soal dapat dilihat sebagai berikut
Dapat dilihat bahwa disini adalah model 3d dengan 5 batang atau elemen. Kita masih menggunakan pemrograman yang sama yang dibuat oleh fahmi, namun kita harus mengubah data-data sesuai dengan soal yang ada. Yang kita ubah pertama pada class adalah data dari parameter realnya, integer, dan boundary. kode pemrograman yang fahmi pakai adalah sebagai berikut :
class QuizSoal1
//inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data
//titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R;
//check force Real [3] F;
equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(n, node, Ke);
KgTot = SumStiffnessMatrixGlobal(Kg);
KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z);
U = GaussJordan(KgB, load);
R = ReactionForce(KgTot, U, load);
F = CheckForce(load,R);
end QuizSoal1;
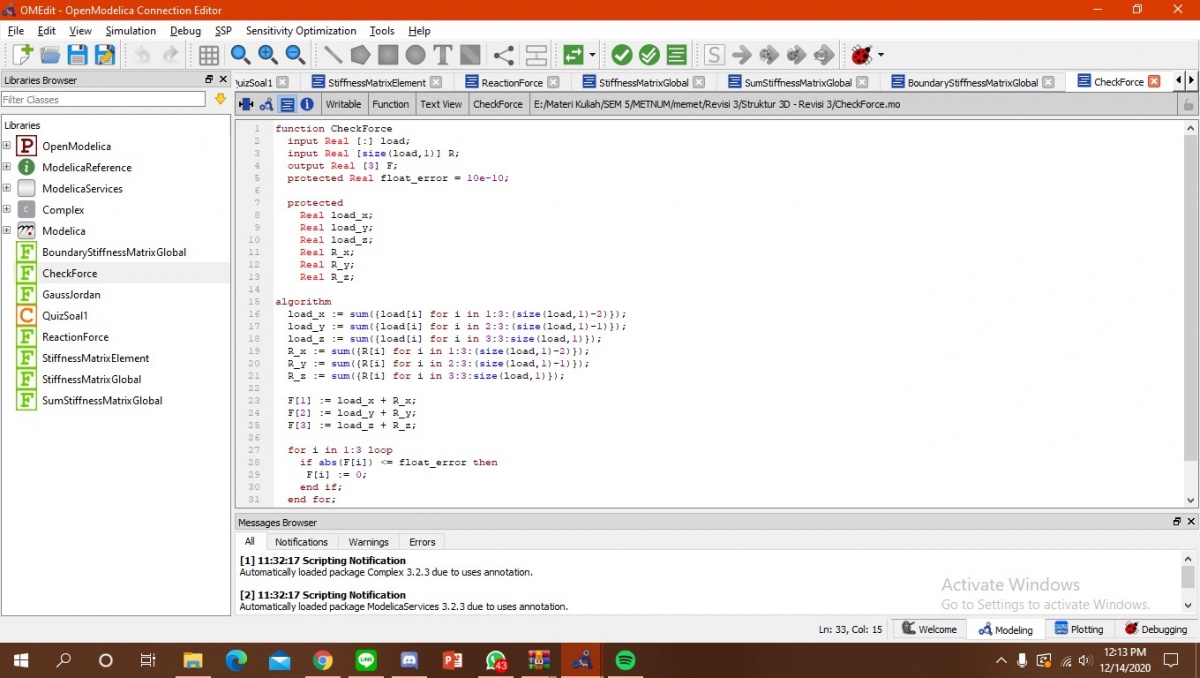
Berikut juga terdapat function untuk perhitungan-perhitungan yang digunakan yang dapat dilihat di bawah ini:
Selanjutnya, simulasi akan dilakukan dengan mengecek model terlebih dahulu apakah sudah benar. Check of QuizSoal1 completed successfully.
Class QuizSoal1 has 1407 equation(s) and 1407 variable(s).
0 of these are trivial equation(s).
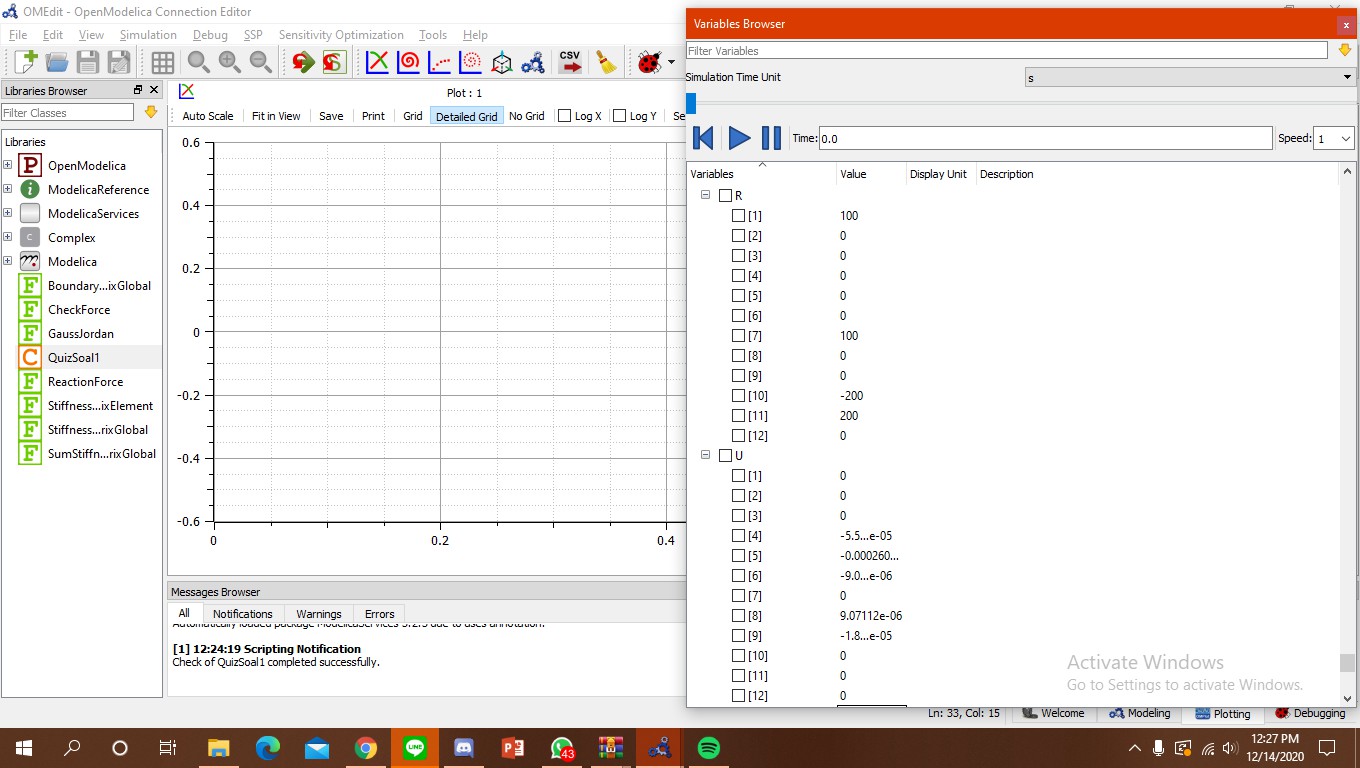
Berikut diatas merupakan hasil dari check model. kemudian akan disimulasikan, Dari simulasi yang sudah dilakukan, dapat dilihat hasil dari U dan R yang akan ditampilkan dibawah ini.
3. Feedback
Sudah sangat baik dan inovatif, namun banyak sekali istilah baru sehingga perlu di jelaskan secara langsung lebih lanjut
Terima kasih
Wassalamualaikum Wr. Wb
Pertemuan 6 : 14 Desember 2020
Assalamualaikum Wr. Wb
Selamat siang semuanya. Pada hari ini kelas dibuka oleh pak Dai dengan membuka diskusi mengenai generasi jaman sekarang lebih mementingkan nilai daripada ilmunya. Pak Dai menjelaskan bahwa kasus itu dibagi 2. yang pertama persoalan yang menyangkut solid mechanics dan yang kedua yaitu fluida dalam teknik mesin ini. Sebenernya semua beban pada dunia nyata adalah dinamik. Namun, beban statik hanya merupakan suatu pendekatan. Itu yang disebut sustain load pada filosofi statika struktur. Pada trusses, stress atau deformasi hanya ada di ujung2nya. Pada trusses saat dipasang, semua titik hanya ada 3 derajat atau variabel yaitu ux, uy, uz. Pada titik tersebut kita dapat menghitung hukum fisikanya. Kita juga menyususn persamaan aljabar disetiap titiknya. Dengan metode numerik kita dapat menyelesaikan persamaan keseluruhan secara global.
Pertemuan 7 : 21 Desember 2020
Asslamualaikum wr wb
pada hari ini, pak Dai membuka kelas dengan menjelaskan kepada kami apa itu optimasi. Pak Dai menjelaskan bahwa tugas besar yang kita buat nantinya harus menganalisa trusses atau rangka. Trusses berbeda dengan beam. Beam ada asumsi momen di setiap titik. Kalau trusses tidak perlu. Dalam metode numerik ini bukan hanya menyelesaikan persamaan namun juga harus bisa menyusun persamaan fisika dan aljabarnya. Tentukan pers. aljabar, analisa dengan matriks, dan selesaikan. menghitung dan mencari kondisi optimal. kalau kita merancang, yang sering menjadi tujuan atau objektif kita adalah harus ada fungsi atau batasan-batasannya. tujuan disini adalah untuk meminimalkan biaya. Constrainnya harus cukup tangguh dan mampu menahan beban. Gaya yang bekerja harus mampu didukung oleh struktur ini. Harus mencari displacement, setelah itu mencari gaya, kemudian verifikasi apa perhitungan sudah betul. Bandingkan stress dan kekuatan material. Tegangan yang terjadi tidak boleh melebihi setengah dari kekuatan atau allowable stressnya.'
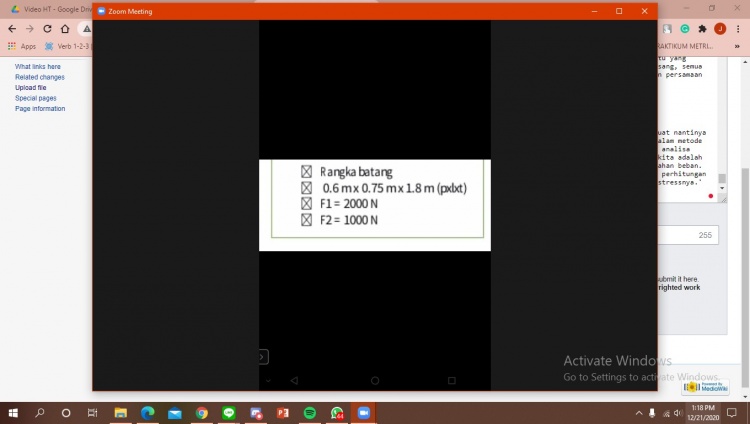
Untuk datanya, rangka batangnya biasanya terdapat seperti pada gambar dibawah ini:
Cari di google spesifikasi material-material besi siku dan harganya. Dari data disitu, kita lakukan optimasi. Contohnya staainless steel lebih mahal tapi lebih kuat. kita harus analisa optimasi sesuai dengan tujuan kita yaitu meminimalkan biaya.
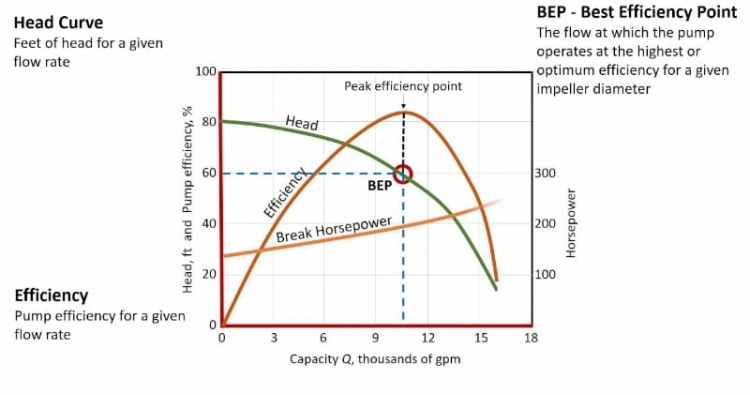
Dapat dilihat pada gambar diatas merupakan ilustrasi daripada optimasi. Dari grafik tersebut, terdapat head, break horse power dan efisiensi. Oleh karena itu, kita harus menemukan BEP atau break even point dimana dapat diketahui pada tingkat efisiensi tertinggi. Sehingga kita harus memastikan bahwa sistem harus seoptimal mungkin dengan menentukan BEP
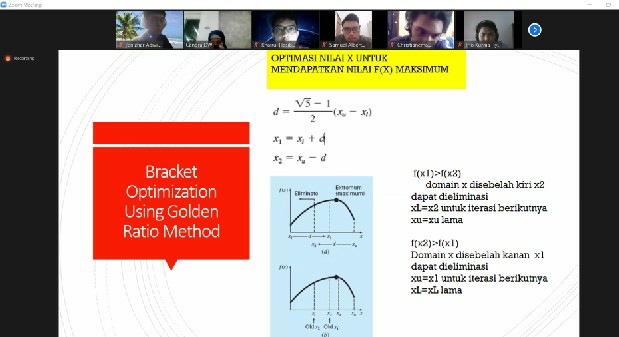
Selanjutnya, kami diberikan tutorial optimasi oleh bu Chandra. Harus ada tujuan dan constraint pada optimasi. Bu chandra menjelaskan mengenai Bracket Optimization Using Golden Ratio Method. Berikut rumus persamaan yang digunakan :
1. d = (sqrt 5 - 1)/2 . (Xu - Xt)
2. X1 = Xt + d
3. X2 = Xu - d
Berikut merupakan cara untuk menentukan global maksimum. Pada gambar diatas merupakan gambaran cara kita mengoptimasikan sebuah persamaan dari grafik. karena kita mengincar efisiensi maksimal, maka kita mengeliminasi pelan-pelan pada setiap iterasinya yang pada bagian sebelah kiri x2. Kemudian bu Chandra memberikan kami latian soal dengan persamaan
F(x) = 2sinx - x^2/10
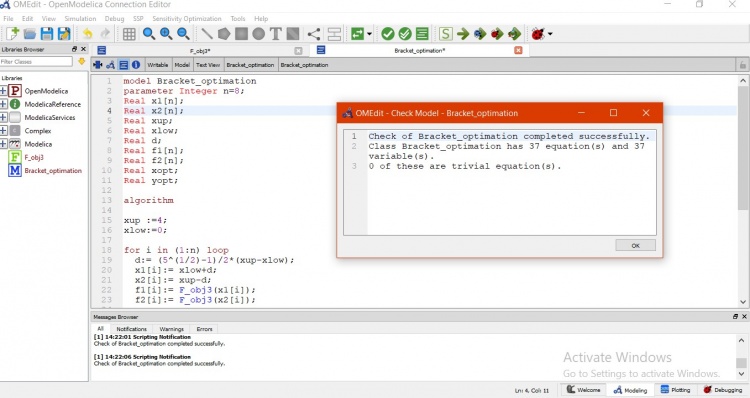
Tujuan objektifnya adalah mencari f(x) maksimum dari fungsi tersebut. Untuk constraint tidak ada. Constraint ada kalau x dibatasi. Kami kemudian menuliskan program pada open modelica sebagai berikut
Kemudian, berikutnya adalah kami membuat model untuk menyelesaikan persamaan tersebut. Model tersebut dapat dilihat sebagai berikut :
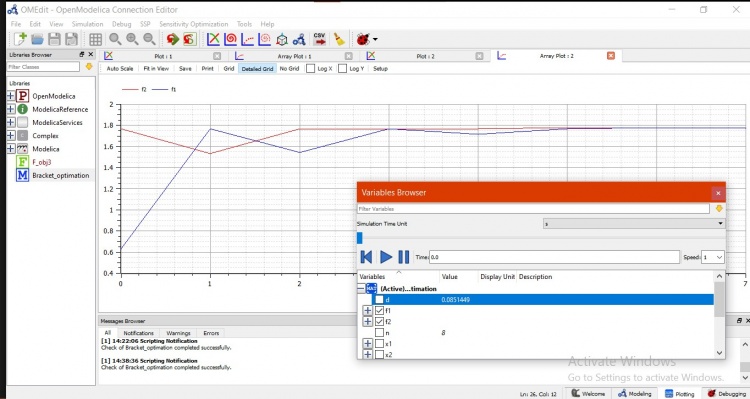
Kemudian berikutnya merupakan hasil grafik f1 dan f2 pada simulasi kodingan diatas
Sekian
Terima kasih
Wassalamualaikum Wr. Wb
TUGAS BESAR METODE NUMERIK
Assalamualaikum Wr. Wb
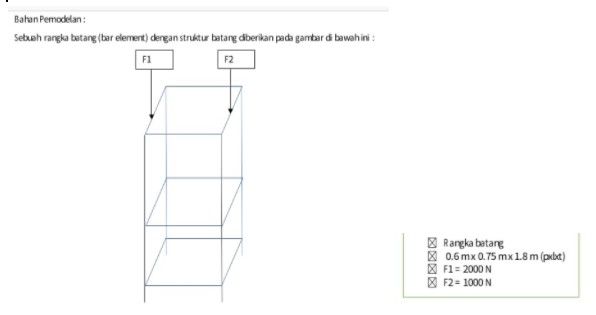
Berikut merupakan sinopsis tugas besar yang diberikan oleh pak Dai. Diberikan permodelan 3d trusses yang diberikan sebuah gaya seperti gambar dibawah ini:
Berikut merupakan alur dari mengerjakan tugas besar yang sudah didiskusikan bersama dengan Josiah, Fahmi, dan christo. Alur ini sangat membantu saya dalam memahami tahap-tahap pengerjaan yang tadinya belum terbayang sama sekali. berikut merupakan penjabaran dari alur tersebut.
1. Mendefinisikan Permasalahan
Gambar diatas merupakan suatu model trusses yang akan dioptimasi. Optimasi memiliki tujuan objektif yaitu menekan biaya namun dengan material yang terbaik. Oleh karena itu, disini saya ingin mengoptimasi model trusses ini dengan membandingkan beberapa material untuk nantinya memilih material yang sesuai dengan metode numerik.
2. Asumsi Solusi
Berikut merupakan asumsi-asumsi yang saya gunakan untuk mencari solusi dari soal diatas.
1. Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
2. Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
Membandingkan material – material dengan data dan persoalan yang ada. Pertama-tama kita memilih material yang terbaik terlebih dahulu dengan mengasumsikan dengan luas tertentu sehingga kita dapat membandingkan elastisitas dari beberapa material tersebut. Dari perbandingan tersebut, kita memakai material yang terbaik namun disini kita juga memperhatikan biaya dari material tersebut. Berikutnya, apabila kita sudah mendapatkan material yang paling efisien, kita membandingkan berbagai macam variable area yang nantinya paling sesuai dengan tujuan objektif dari optimasi.
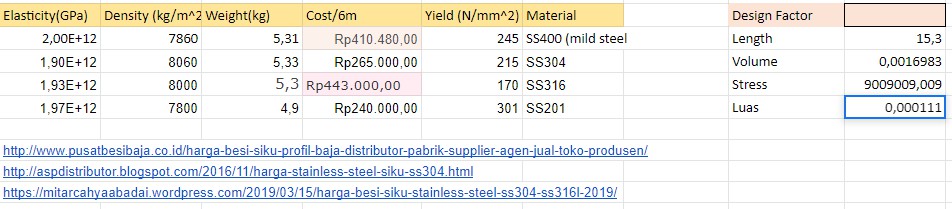
3. Pengambilan Data
Disini saya mengambil data berbagai macam amterial dengan profil besi siku dan daftar harganya juga. Berikut merupakan tabel dari pengambilan data untuk material yang bervariasi.
4. Permodelan Numerik
Sebelumnya, saya menggunakan curve fittin guntuk melakukan pendekatan -pendekatan terhadap sampel -sampel data yang sudah diambil. Berikut merupakan kode syntax untuk curve fitting yang saya gunakan. Coefficient yang didapatkan diakhir hasil merupakan koefisien yang dimasukkan ke rumus untuk menghasilkan pendekatan-pendekatan tersebut. berikut merupakan kode syntx saya
class curve_fitting
parameter Real X[4]={2.00E+12,1.90E+12,1.93E+12,1.97E+12}; //Area/ Elastisitas parameter Real Y[4]={410480,265000,443000,240000}; //Area/ Cost/ Density/ Yield
Real Coe[3];
algorithm Coe:=Curve_Fitting(X,Y,2);
end curve_fitting;
Untuk fungsi curve fittingnya, saya menggunakan kodingan yang sudah didiskusikan bersama dengan fahmi, josiah, dan christo. Kode synaxnya adalah sebagai berikut
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for;
end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting; /* for i in 1:3 loop
for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R);
end for;
- /
untuk permodelan numerik, berikur merupakan kode syntax yang sudah didiskusikan bersama-sama
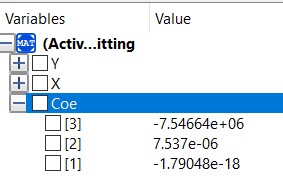
5. Komputasi
Memulai perhitungan numerik dan mensimulasikannya agar mendapat Analisa-analisa yang dibutuhkan untuk nantinya di optimasi. Berikut merupakan hasil dari kodingan curve fitting saya yang membuahkan hasil berupa coefficient untuk Area locked
6. Optimasi 1
7. Optimasi 2