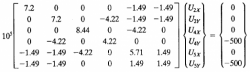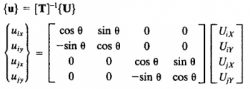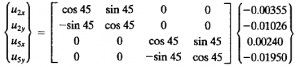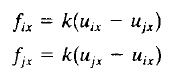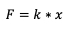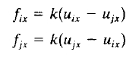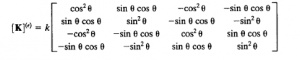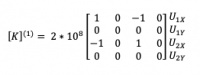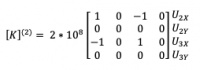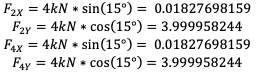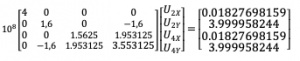Metnum03-Addarda Irsyad Usman
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Bio Data
Kelas Metode Numerik - 03
Nama : Addarda Irsyad Usman
NPM : 1706021556
Program Studi : S1 Teknik Mesin Parallel
Contents
- 1 Bio Data
- 2 Kelas Metode Numerik
- 3 Pertemuan 1 (Senin, 9 November 2020)
- 4 Pertemuan 2 (Senin, 16 November 2020)
- 5 Pertemuan 3 (Senin, 23 November 2020) Tugas Studi Kasus Gambar 12.11
- 6 Pertemuan 3 (Senin, 23 November 2020) PR
- 7 Pertemuan Ke4 (30 November 2020)
- 8 Jawaban Soal Quiz
- 9 Pertemuan 5 (Senin, 7 Desember 2020)
- 10 Pertemuan Ke6 (13 Desember 2020)
- 11 Pertemuan Ke7 (21 Desember 2020)
- 12 Tugas Besar
Kelas Metode Numerik
Pertemuan 1 (Senin, 9 November 2020)
Assalamualaikum Wr. Wb.
Pada pertemuan pertama kali ini dapat dianggap sebagai pengenalan dari Pak Dai tentang bagaimana metode pembelajaran kelas Metode Numerik - 03 bersama Pak Dai. Banyak diskusi yang terjadi pada pertemuan ini, sebagaimana Pak Dai mengarahkan kami untuk melakukan diskusi 2 arah ini. Pembahasan menarik mengenai fenomena numerik yang berada di kehidupan dasar manusia ketika menemukan bilangan-bilangan yang berupa konsep seperti "tak terhingga" atau "infiniti" dan bagaimana pandangan kita sebagai seorang engineer.
Kemudian Pak Dai menjelaskan bahwa pemberian materi akan berupa pengaplikasian dari metode numerik yang akan menggunakan software Open Modelica. Software ini merupakan program yang dapat menyimulasikan suatu sistem dengen data input kode sumber atau biner untuk melakukan suatu penelitian terhadap sistem tersebut. Setiap mahasiswa diharapkan memiliki software tersebut sebagai penunjang pembelajaran setengah semester kedepan.
Pertemuan 2 (Senin, 16 November 2020)
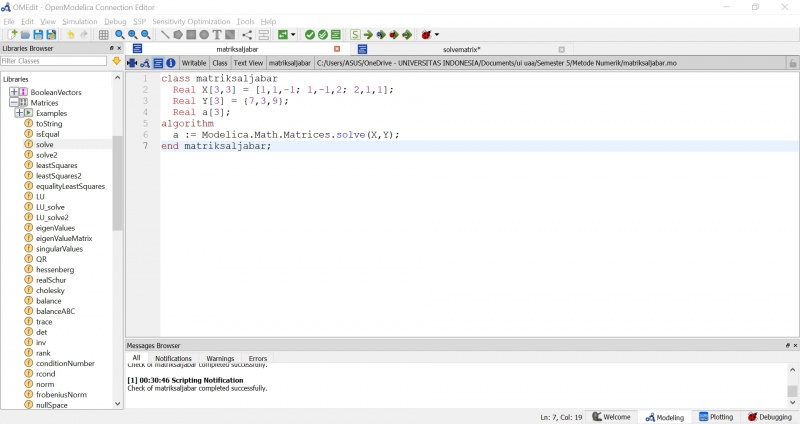
Pada pertemuan kedua ini, kami mempelajari cara membuat program sederhana pada modelica untuk menghitung jumlah dan rata-rata angka. Diakhir kelas kami ditugaskan untuk membuat suatu program untuk menyelesaikan persamaan aljabar simultan, berikut merupakan program yang saya buat:
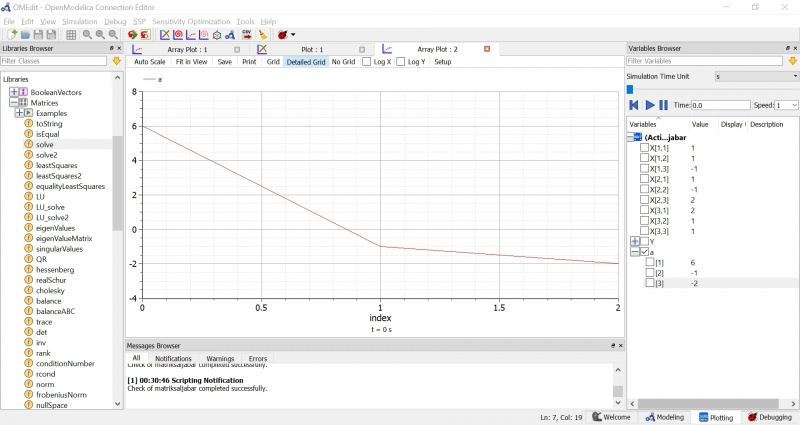
Saya menggunakan matriks berukuran 3 x 3 dengan metode gauss elimination dan function solve yang disediakan oleh software modelica sehingga mendapatkan hasil [6, -1, -2]
Pertemuan 3 (Senin, 23 November 2020) Tugas Studi Kasus Gambar 12.11
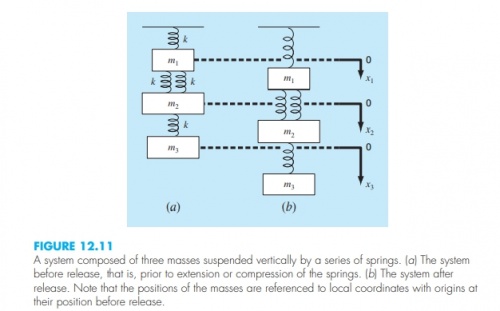
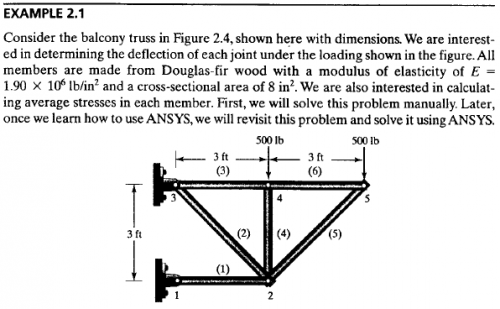
Pada pertemuan ketiga ini, kami diminta untuk membuktikan suatu studi berdasarkan gambar 12.11, serta juga dengan matriks yang tertera pada buku panduan Numerical Methods for Engineers 7th Edition superti berikut merupakan gambar 12.11:
Berikut merupakan program yang saya buat pada program Open Modelica menggunakan metode Gauss Elimination sebagai pembuktian terhadap persamaan yang bereda di buku panduan. Dapat disimpukan bahwa persamaa berdasarkan buku panduan terbuktinya persamaan tersebut dengan mengacu pada nilai a pada Open Modelica berikut. Maka Open Modelica berikut terbukti dapat menyelesaikan persamaan yang sama seperti di buku panduan dengan hasil yang sama pula.
Hasil yang didapatkan dari simulasi di atas adalah sebagai berikut
a1 = 7.3575
a2 = 10.0552
a3 = 12.5077
Pertemuan 3 (Senin, 23 November 2020) PR
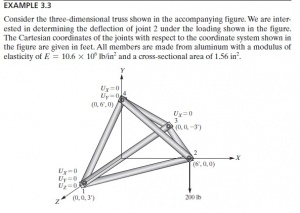
Pada pertemuan ini Pak Dai juga memberikan PR kepada kami untuk menyelesaikan soal berikut:
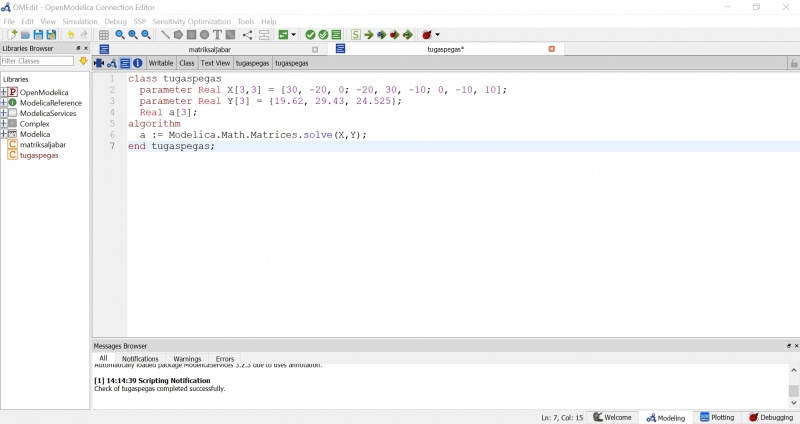
Pada tugas ini diberikan juga penjelasan mengenai bagaimana persamaan akhir menggunakan Hukum Hooke, dimana matriks adalah sebagai berikut:
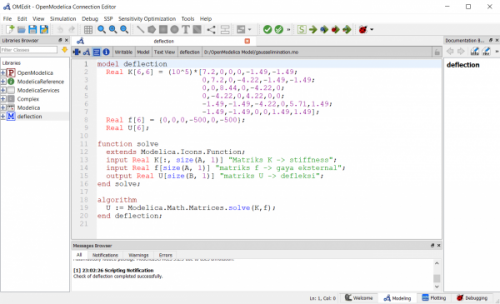
Pada penyelesaiannya dapat menggunakan OpenModelica sebagai berikut
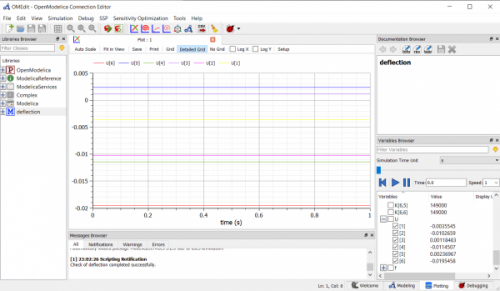
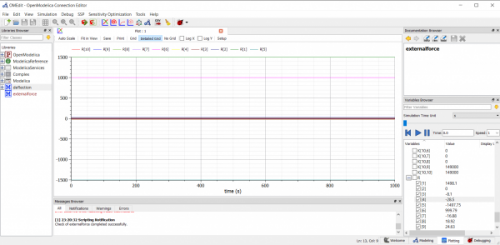
Dan juga saya berikan plotting menggunakan Open Modelica
Soal mempertanyakan mengenai nilai gaya reaksi terhadap gambar, maka diperlukan perhitungan untuk mendapatkan nilai gaya reaksi.
Menggunakan OpenModelica dapat menyelesaikan persamaan tersebut, menggunakan program sebagai berikut
Serta dengan hasil plottingnya
Relain itu tugas ini juga membutuhkan perhitungan normal stress dan gaya internal pada gambar. Pada perhitungan normal stress diperlukan transformasi dari hasil defleksi ditinjau dari koordinat global menjadi transformasi lokal, dimana menggunakan persamaan berikut
Pada análisis stress Elemen 5, maka node yang dianalisis adalah node 2 dan 5. Sehingga persamaan matriks defleksi pada koordinat lokal menjadi
Menggunakan OpenModelica dengan program sebagai berikut untuk dapat menyelesaikan permasalahan
Didapatkan juga hasil plotting
Maka didapatkan
U2x = -0.00976 inch
U6x= -0.01209 inch
Dan untuk internal force didapatkan melalui persamaan
didapatkan nilai internal force elemen 5 sebesar 696 lb
Pertemuan Ke4 (30 November 2020)
Berikut merupakan hasil jawaban Soal No 4 dan No 8 saya
Jawaban Soal Quiz
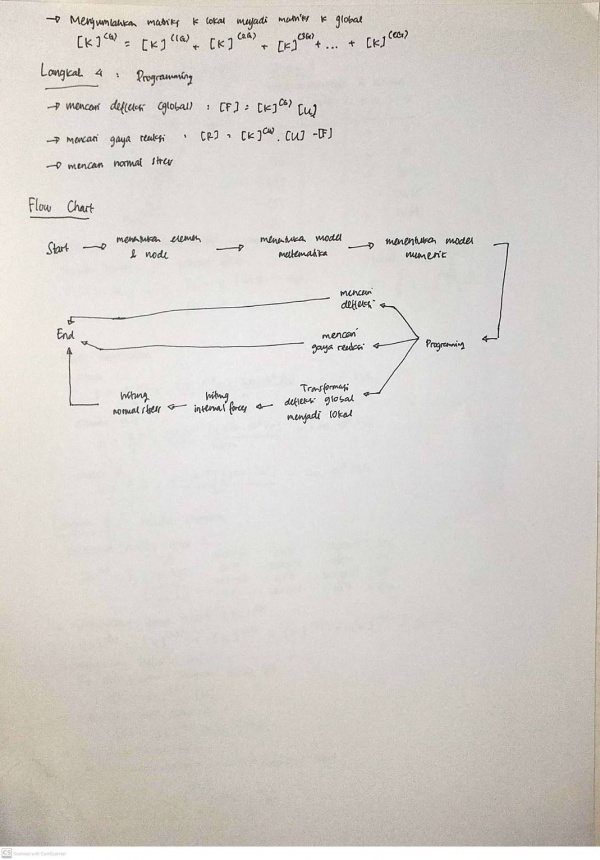
Berikut merupakan penyelesaian dari flowchart Nomor 4
1. Mendefinisikan Node & Elemen
Kita perlu mendefinisikan setiap elemen dan node nya untuk mendapatkan derajat yang digunakan pada elemen dan node tersebut
2. Membuat Model Matematika
Dikarenakan kita mencari defleksi dari gambar yang tersedia, maka akan digunakan persamaan persamaan berikut
a. Hukum Hooke
b. Internal Force
c. Normal Stress
Selain itu kita juga perlu untuk menentukan nilai kekakuan dari setiap elemen
3. Membuat Model Numerik
Setelah mendefinisikan elemen dan node, sert menentukan model matematika yang akan kita gunakan, kita dapat membuat model numerik dari gambar. Untuk menentukan matriks kekakuan elemen dapat menggunakan Persamaan matriks berikut.
a. Analisis Elemen
Karena elemen 1,2 sejajar dengan sumbu X global maka nilai θ = 0, dan didapatkan hasil analisis elemen 1,2
Elemen 1 dan posisi Elemen 1 di matriks global
Elemen 2 dan posisi Elemen 2 di matriks global
Dikarenakan elemen 3 sejajar dengan sumbu Y global maka nilai θ = 90, dan didapatkan hasil analisis elemen 3
Elemen 3 dan posisi Elemen 3 di matriks global
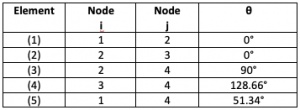
Untuk analisis Elemen 4,5 dapat dihitung terlebih dahulu derajatnya dari data yang telah disediakan gambar, maka didapatkan θ4 = 51,34 dan θ5 = 128,66. Maka dapat didapatkan hasil analisis elemen 4,5
Elemen 4 dan posisi Elemen 4 di matriks global
Elemen 4 dan posisi Elemen 4 di matriks global
4. Menghitung Defleksi (Koordinat Global)
Setelah mendapatkan seluruh matriks global elemen 1,2,3,4,5 maka kita dapat menggabungkan seluruh matriks tersebut menjadi matriks global [K](G), melalui persamaan berikut.
yang menghasilkan
Kondisi batas yang diperlihatkan gambar membuat kondisi node 1 dan 3 adalah fixed dan kondisi tersebut menyatakan bahwa node 2 dan 4 diberikan beban eksternal sehingga
Dengan menerapkan Hukum Hooke F= k.x, maka dalam persamaan matrix menjadi [F]=[K(G)].[U¬(e)], sehingga didapatkan dan disederhanakan menjadi:
Pertemuan 5 (Senin, 7 Desember 2020)
Pada pertemuan kali ini, kelas membahas tentang tugas yang diberikan minggu lalu. Tugas kemarin merupakan pembahasan mengenai gaya reaksi pada elemen beam penyusun statika struktur. Kemudian dilanjutkan dengan pembahasan tugas dari beberapa rekan saya. Pertemuan ini menjelaskan hasil dari tugas rekan kami, Ahmad Mohammad Fahmi, mensenai coding yang ia buat pada tugas minggu lalu tentang Plane Truss dan Space Truss.
Diskusi berlangsung cutup interaktif dengan penjelasan dari Fahmi sendiri mengenai hasil tugas ia. Namun, masih banyak hal yang belum saya sepenuhnya mengerti, walau begitu tetap meneruskan progress diskusi pada platform ini. Soal baru diberikan kepada kami dari Pak Dai sebagai berikut
Mempelajari Coding 3D Fahmi
Pada algoritma Ahmad Muhammad Fahmi, metode yang digunakan untuk penyelesaian sama dengan flowchart yang sudah saya buat untuk Quiz. Penyelesaian kedua soal ini memiliki parameter input:
1. A (Luas Permukaan)
2. E (Modulus Elastisitas)
3. node
4. load
Pada algoritma ini dibuat terlebih dahulu beberapa function untuk mempermudah pemanggilan pada class. Disini terdapat function yaitu Stiffness Matrix Global, Sum Stiffness Matrix Global, Boundary Stiffness Matrix Global, Gauss Jordan, Reaction Force, dan Check Force.
Pengaplikasian Coding Terhadap Soal
Berikut
|
Stiffness Matrix Element Function function StiffnessMatrixElement
input Real [:,6] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] L;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,2]/L[i];
cos_y := inisiasi_mat[i,3]/L[i];
cos_z := inisiasi_mat[i,4]/L[i];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
|
|
Stiffness Matrix Global Function function StiffnessMatrixGlobal input Integer x; input Integer [:,2] n; input Real [:,6,6] Ke_mat; output Real [size(Ke_mat,1),3*x,3*x] Kg_mat; algorithm Kg_mat := zeros(size(Ke_mat,1),3*x,3*x); for i in 1:size(Ke_mat,1) loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal; |
|
Sum Stiffness Matrix Element Function function SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
|
|
Boundary Stiffness Matrix Global Function function BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met;
input Integer[:] Boundary_xyz;
input Integer[:] Boundary_xy;
input Integer[:] Boundary_xz;
input Integer[:] Boundary_yz;
input Integer[:] Boundary_x;
input Integer[:] Boundary_y;
input Integer[:] Boundary_z;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end BoundaryStiffnessMatrixGlobal;
|
|
Gauss Jordan Function function GaussJordan input Real [:,:] KgB_met; input Real [size(KgB_met,1)] load_met; output Real [size(KgB_met,1)] U_met; protected Real float_error = 10e-10; algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan; |
|
Reaction Force Function function ReactionForce input Real [:,:] KgTot_met; input Real [size(KgTot_met,1)] U_met; input Real [size(KgTot_met,1)] load_met; output Real [size(KgTot_met,1)] R_met; protected Real float_error = 10e-10; algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce;
|
|
Check Force Function function CheckForce
input Real [:] load;
input Real [size(load,1)] R;
output Real [3] F;
protected Real float_error = 10e-10;
protected
Real load_x;
Real load_y;
Real load_z;
Real R_x;
Real R_y;
Real R_z;
algorithm
load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
load_z := sum({load[i] for i in 3:3:size(load,1)});
R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
R_z := sum({R[i] for i in 3:3:size(load,1)});
F[1] := load_x + R_x;
F[2] := load_y + R_y;
F[3] := load_z + R_z;
for i in 1:3 loop
if abs(F[i]) <= float_error then
F[i] := 0;
end if;
end for;
end CheckForce; |
Berikut merupakan class yang digunakan untuk memanggil function diatas dan menyelesaikan Example 3.3
|
Class class QuizSoal1
//inisiasi = [ elemen#, dX, dY, dZ, A, E]
parameter Real [:,6] inisiasi = [1, 6, 0, -3, 1.56, 10.6e6; //isi sesuai data
2, 0, 0, -6, 1.56, 10.6e6;
3, 0, 6, -3, 1.56, 10.6e6;
4, -6, 0, -3, 1.56, 10.6e6;
5, -6, 6, 0, 1.56, 10.6e6;
6, 0, 6, 3, 1.56, 10.6e6];
//node = [ i, j]
parameter Integer [size(inisiasi,1),2] node = [1, 2; //isi sesuai data
1, 3;
1, 4;
2, 3;
2, 4;
3, 4];
//jumlah node parameter Integer n = 4; //isi sesuai data //titik node boundary xyz
parameter Integer [:] Boundary_xyz = {1}; //isi sesuai data
//titik node boundary xy
parameter Integer [:] Boundary_xy = {4}; //isi sesuai data
//titik node boundary xz
parameter Integer [:] Boundary_xz = {0}; //isi sesuai data
//titik node boundary yz
parameter Integer [:] Boundary_yz = {0}; //isi sesuai data
//titik node boundary x
parameter Integer [:] Boundary_x = {3}; //isi sesuai data
//titik node boundary y
parameter Integer [:] Boundary_y = {0}; //isi sesuai data
//titik node boundary z
parameter Integer [:] Boundary_z = {0}; //isi sesuai data
//load = [ F1x, F1y, F1z,..., Fnx, Fny, Fnz]
parameter Real [3*n] load = {0, 0, 0, //isi sesuai data
0, -200, 0,
0, 0, 0,
0, 0, 0};
Real [size(inisiasi,1)] L; Real [size(inisiasi,1)] k; Real [size(inisiasi,1),6,6] Ke; Real [size(inisiasi,1),3*n,3*n] Kg; Real [3*n,3*n] KgTot; Real [3*n,3*n] KgB; Real [3*n] U; Real [3*n] R; //check force Real [3] F; equation
L = {(sqrt(inisiasi[i,2]^2 + inisiasi[i,3]^2 + inisiasi[i,4]^2)) for i in 1:size(inisiasi,1)};
k = {(inisiasi[i,5] * inisiasi[i,6] / L[i]) for i in 1:size(inisiasi,1)};
Ke = StiffnessMatrixElement(inisiasi); Kg = StiffnessMatrixGlobal(n, node, Ke); KgTot = SumStiffnessMatrixGlobal(Kg); KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary_xyz, Boundary_xy, Boundary_xz, Boundary_yz, Boundary_x, Boundary_y, Boundary_z); U = GaussJordan(KgB, load); R = ReactionForce(KgTot, U, load); F = CheckForce(load,R); end QuizSoal1; |
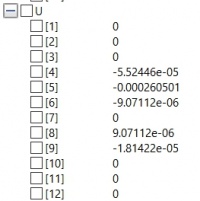
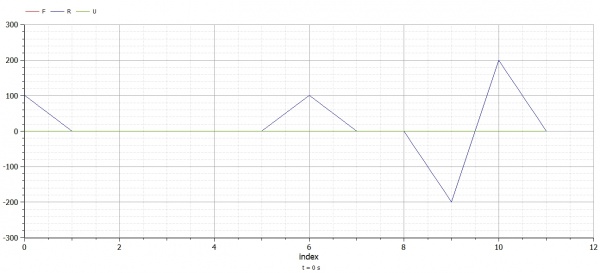
Berikut merupakan hasil dan grafik yang didapat
Pertemuan Ke6 (13 Desember 2020)
Pada pertemuan ini, Pak Dai memperykuat pemahaman tentang ilmu yang kami dapat selama di Mata Kuliah Metode Numerik. Dilanjutkan dengan permintaan dari Pak Dai untuk para peserta melakukan muhasabah terhadap ilmu yang telah didapatkan selama kelas ini berjalan.
Pertemuan Ke7 (21 Desember 2020)
Pada pertemuan hari ini, Pak Dai dan menjelaskan mengenai Tugas Besar yang diberikan kepada kami yaitu Aplikasi Metode Numerik dalam Optimasi Desain Struktur Rangka Sederhana. Optimasi pada tugas ini adalah optimasi terhadap rangka yang dituju dengan tujuan untuk mencari material yang paling tepat untuk menjadi material rangka tersebut. Salah satu praktik optimasi adalah Bracket Optimization Using Golden Ratio Method yang dilanjutkan oleh Bu Candra.
Tugas Besar
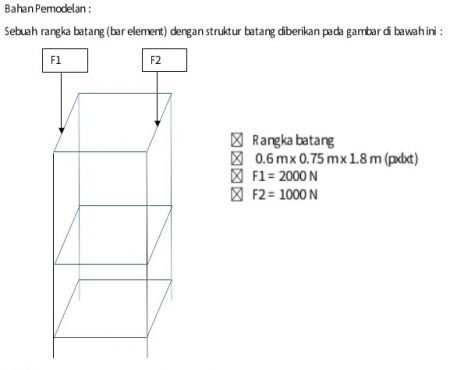
Pada tugas besar ini kami diminta untuk mencari optimasi pemilihan material untuk rangka berikut. Optimasi pemilihan material bergantung kepada 2 hal yaitu optimasi elastisitas dan optimasi luas penampang.
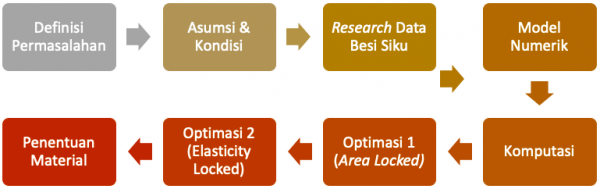
Flow Chart
Untuk mempermudah pengerjaan dari tugas besar ini, dibuatlah sebuah flowchart agar dapat lebih mudah untuk dimengerti.
Definisi Permasalahan
Pada soal yang tertera di atas, kami diminta untuk mencari optimasi pemilihan material atas struktur tsb. Jenis material yang digunakan adalah besi siku (angle bar) yang akan menjadi struktur yang merepresentasikan gambar. Kami harus membandingkan optimasi elastisitas dan optimasi luas penampang dari berbagai material besi siku agar dapat memilih material yang paling efisien dan efektif untuk menjawab tugas ini. Struktur memiliki dimensi (p x l x t) = 0,6m x 0,75m x 1,8m dimana pada baian atas struktur terdapat 2 gaya yang mempengaruhi struktur yaitu F1 = 2000 N dan F2 = 1000 N.
Asumsi dan Kondisi
Penerapan asumsi diberikan kepada tugas ini Karena ada beberapa data yang tidak diketahui untuk menyelesaikan tugas ini. Pada struktur memiliki kendisi dimana beberapa struktur tambahan, yang dianggap sebagai lantai, yaitu berupa struktur penopang dari keseluruhan struktur. Lantai ini tidak diberikan data seperti tinggi dari tanah. Maka dari itu dapat diasumsikan berapa tinggi dari lantai-lantai tersebut. Selain itu node-node juga perlu diasumsikan kepada gambar dan ditentukan agar dapat mempermudah pengerjaan.
Pada penempatan gaya F1 dan F2 yang diberikan kepada struktur hanya akan terdistribusi di point penghubung. Hal ini dikarenakan, struktur pada tugas ini memiliki sıfat truss.
Research Data Besi Siku
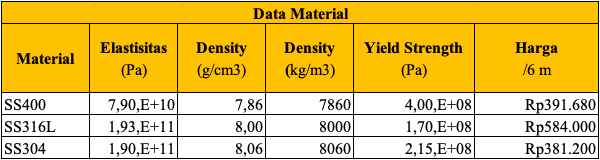
Pada tugas ini, dimensi besi siku saya buat sama pada setiap material, untuk membandingkan dengan persamaan luas penampang dari besi siku. Maka dari itu dimensi besi siku sebagai berikut.
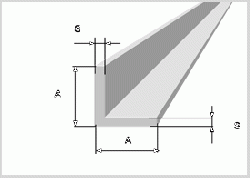
Besi siku memiliki properti-properti yang dibutuhkan untuk membantu pengerjaan tugas ini. Properti material yang dicari merupakan mechanical properties dan harga dari besi siku itu sendiri. Pada pasarnya komoditi besi siku terjual dengan panjang 6 m. Maka dari itu harga jual yang tortera berikut merupakan harga jual per 6 m besi siku. Material yang saya gunakan pada tugas ini adalah SS400, SS316L, dan SS304
Permodelan Numerik
Perhitungan displacement, reaction force, dan stress :
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material
parameter Real Area= (nilai area) ; //Luas Siku
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material
//define connection
parameter Integer C[Trusses,2]=[1,5; //vertical 1st floor
2,6; //vertical 1st floor
3,7; //vertical 1st floor
4,8; //vertical 1st floor
5,6; //horizontal 1st floor
6,7; //horizontal 1st floor
7,8; //horizontal 1st floor
5,8; //horizontal 1st floor
5,9; //vertical 2st floor
6,10; //vertical 2st floor
7,11; //vertical 2st floor
8,12; //vertical 2st floor
9,10; //horizontal 2st floor
10,11; //horizontal 2st floor
11,12; //horizontal 2st floor
9,12; //horizontal 2st floor
9,13; //vertical 3st floor
10,14; //vertical 3st floor
11,15; //vertical 3st floor
12,16; //vertical 3st floor
13,14; //horizontal 3st floor
14,15; //horizontal 3st floor
15,16; //horizontal 3st floor
13,16]; //horizontal 3st floor
//define coordinates (please put orderly)
parameter Real P[Points,3]=[ 0 ,0 ,0,1,1,1; //1
0.75,0 ,0,1,1,1; //2
0.75,0.6,0,1,1,1; //3
0 ,0.6,0,1,1,1; //4
0 ,0 ,0.3,0,0,0; //5
0.75,0 ,0.3,0,0,0; //6
0.75,0.6,0.3,0,0,0; //7
0 ,0.6,0.3,0,0,0; //8
0 ,0 ,1.05,0,0,0; //9
0.75,0 ,1.05,0,0,0; //10
0.75,0.6,1.05,0,0,0; //11
0 ,0.6,1.05,0,0,0; //12
0 ,0 ,1.8,0,0,0; //13
0.75,0 ,1.8,0,0,0; //14
0.75,0.6,1.8,0,0,0; //15
0 ,0.6,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
Kurva Curve Fitting
model Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;