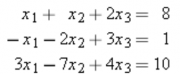Muhammad Helmy Yusuf
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
| Muhammad Helmy Yusuf | |
|---|---|

| |
| Nama Lengkap | Muhammad Helmy Yusuf |
| NPM | 1906301236 |
| Jurusan | Teknik Mesin |
| Alamat Surel | muhammad.helmy@ui.ac.id |
Muhammad Helmy Yusuf (lahir di Kebumen, 13 Juni 2001; umur 19 tahun) adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Selain menjalankan tugas utama menjadi mahasiswa, Helmy dikenal aktif dalam berorganisasi dan aktif melakukan kegiatan sosial yang dapat bermanfaat dan berdampak untuk orang lain.
Contents
[hide]Mukadimah
Helmy lahir di Kebumen, Jawa Tengah. Saat sebelum dilahirkan, orang tuanya mengubah namanya hingga 5 kali. Mereka akhirnya memberi nama Helmy, yang Yusuf diberi oleh ibunya dengan harapan menjadi pribadi penyabar dan tumbuh menjadi laki - laki pemaaf dan setampan Nabi Yusuf AS serta memiliki kepribadian luhur seperti Nabi Muhammad SAW.
Helmy menjalani proses pendidikan dasar hingga SMA di Kota Depok. Semasa pendidikannya, Helmy juga aktif dalam berbagai kegiatan ekstrakulikuler sekolah seperti mengikuti Futsal maupun rohani Islam di sekolahnya dan berhasil menjuarai berbagai macam turnamen olahraga maupun akademis. Sehabis menyelesaikan pendidikan SMA-nya di SMAN 2 Depok, pada tahun 2019 ia mengambil jurusan Teknik Mesin di Universitas Indonesia.
Selama berkuliah, Helmy juga mengikuti beberapa organisasi, kepanitiaan, bahkan kegiatan sosial pun pernah diikuti. Saat ini ia menjabat sebagai Badan Pengurus Penelitian dan Pengembangan (LITBANG) di IMM FTUI dan TIS FTUI. Tak hanya di lingkup kampus, ia juga mengikuti organisasi kepemudaan di Indonesia bernama Young On Top dan pernah menjadi Project Officer dalam acara organisasi tersebut. Di TIS FTUI, ia juga menjadi kesatria pengajar dimana mengajar anak-anak di lapak pemulung daerah karang pola, Pasar Minggu, Jakarta Selatan. Melalui hal-hal yang diikutinya membuat Helmy memiliki skill dalam mengolah data, menganalis, mengevaluasi suatu hal berdasarkan data yang diperoleh, dan skill manajemen personal yang baik. Selain itu juga tumbuh kepedulian terhadap sesama dalam dirinya.
Metode Numerik
Metode numerik merupapakan teknik dalam penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik.
Pada kelas Metode Numerik-02 semester gasal 20120/2021, perkuliahan pekan pertama sampai UTS diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Dimana telah membahas materi seperti:
- Pseudocode
- Sistem Persamaan
- Turunan Numerik
- Metode Newton Rhapson, Secant, dan Bisection
- Regresi Linear
- Interpolasi
Barulah sehabis UTS proses pembelajaran diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Pertemuan Perkuliahan
Pertemuan Pertama (Rabu, 11 November 2020)
Pada pertemuan pertama setelah UTS diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara. Dimana dijelaskan terkait esensi atau tujuan pembelajaran metode numerik, yaitu:
1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti:Persamaan algoritma, aljabar, pencocokan kurva, persamaan diferensial parsial, dan lainnya
2. Mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik
3. Mampu menerapkan metode numerik dalam hal terkait persoalan keteknikan
4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab
Selain empat poin tersebut, kami juga mendapat pelajaran terkait awalan memakai OpenModelica. Dimana kami diperlihatkan praktek sederhana penggunaan OpenModelica ini. Hingga kami tahu bila komputer selain dapat membantu dalam menyelesaikan permasalahan namun juga memiliki batasan atau limit tertentu seperti tidak mampu menentukan nilai 1/0 yang hanya Tuhan yang tahu nilainya. Pelajaran yang dapat dipetik dari kejadian ini ialah kita sebagai manusia haruslah beriman dan jangan pernah melupakan Tuhan yang mengetahui segalanya.
Tugas 1
Pada pertemuan pertama setelah UTS pada tanggal 11 November 2020, kami diminta untuk mempelajari dan memahami penggunaan OpenModelica. Dimana OpenModelica ini merupakan suatu software yang menggunakan bahasa program modelica untuk melakukan simulasi dan perhitungan lainnya. Untuk mempelejarinya saya belajar dari beberapa sumber di YouTube, saya menonton beberapa video dari youtube dalam proses pembelajarannya. Berikut adalah yang telah saya tonton:
Selain itu kami diminta membuat video hasil pembelajaran dan pada video kali ini, saya akan menjelaskan terkait apa yang sudah saya pelajari tentang open modelica dan juga penerapan atau simulasi sederhananya. Berikut rekaman videonya:
pengalaman perdana saya setelah mencobanya, saya merasakan disini menyediakan beberapa fitur yang ramah pengguna untuk membuat, menjelajah, mengedit, dan mensimulasikan model.
Pertemuan Kedua (Rabu, 18 November 2020)
Pada pertemuan kedua ini diawali dengan penjelasan pak Dai tentang orang yang beruntung itu adalah orang yang menjalani hari ini lebih baik dari hari kemarin, dimana memiliki gradien hidup positif. sedangkan apabila masih sama saja berarti gradiennya 0. Bila lebih buruk dari hari kemarin gradiennya negatif. Jadi usahakan untuk lebih baik dari hari sebelumnya dan terus bersikap positif. Kami juga dijelaskan bahwa setiap bahasa ada compilernya, compiler biasa digunakan untuk program komputer yang menerjemahkan program yang ditulis dalam bahasa pemograman tingkat tinggi seperti fortran, pascal, basic, c++ itu diterjemahkan kedalam bahasa mesinnya. Compiler juga berpengaruh ke kecepatan pemrosesannya karena kodingnya akan berbeda beda yang dihasilkan meskipun prinsipnya sama. Compiler biasanya untuk mahasiswa engineering diantaranya fortran dan c karena engineering sangat penting untuk kecepatan perhitungan itu.
Modelica ,singkatnya adalah sebuah bahasa, namun bukan bahasa pemograman/koding. sebenernya koding hanya saja lebih ke bahasa pemodelan. Modelica dibuat dan di desain untuk bahasa pemodelan, dan bukan semata mata untuk bahasa koding seperti python, c, c++ dsb. klo modelica itu bahasa pemodelan. Namun dalam melakukan perhitungannya, sebelom melakukan perhitungan, kode kita yg dituliskan di modelica itu diterjemahkan dulu dalam bahasa c. setelah itu baru dikompilasi ke dalam bahasa mesin baru dapat executable file nya. Kemudian ketika klik simulate lama karena butuh waktu menerjemahkan bahasa modelica ke bahasa c kemudian juga mencompile ke bahasa mesinnya/komputer. sehingga dapat file yg dapat dieksekusi. kalau mau cepat menggunakan parameter-parameter yang dirubah itu dalam bentuk syntaxnya itu parameter, sehingga kita bisa merubah nilainya kemudian tanpa mensimulate ulang.
Di dalam OpenModelica juga memiliki nilai plus. yaitu : *(+) Bukan semata - mata bahasa koding, namun dia bahasa pemodelan. Dimana kita seorang engineering yang memang bukan khusus membuat koding, tapi kita membuat model dan cocok untuk insiyur, juga perhitungannya lumayan cepat juga banyak penggunanya. dan banyak aplikasi2 yg dikembangkan disini *(+) Memudahkan kita untuk cross function atau mempelajari berbagai dasar ilmu dalam 1 software *(+) Open teknologi dan free. beda dengan mathlab dan lainnya yg berbayar
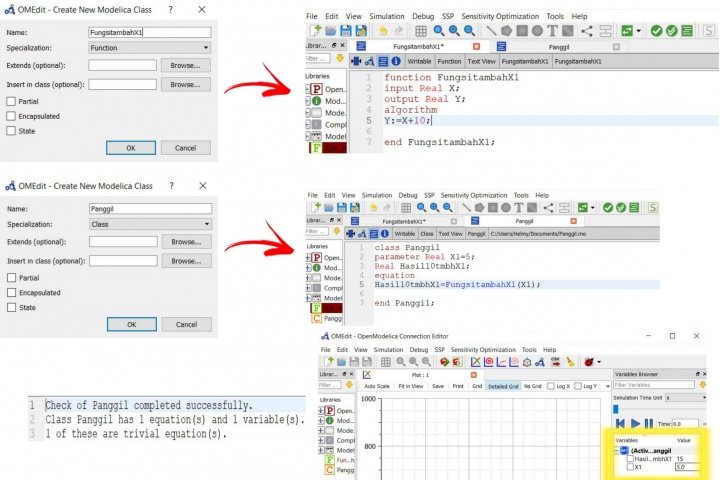
Selanjutnya, Pak Dai juga memerintahkan kami untuk ikut mencoba membuat sebuah function dan class yang nantinya akan dihubungkan. Lewat Share screen yang dipandu oleh Pak Dai, saya mulai mencoba dan mendapatkan hasil yang sama. Ilustrasinya sebagai berikut:
Fungsi yang dibuat yaitu "Fungsi Tambah X1" dengan X sebagai input, Y sebagai output, dan Fungsi yang dibuat adalah Y=10+X. Setelah itu membuat class "Panggil" dimana berfungsi untuk memanggil fungsi tambah X1 yang tadi dibuat. Untuk mendapatkan nilai output Y maka dimasukkanlah nilai input X1. Contohnya saat dibimbing oleh Pak Dai, kami memasukkan X1 sebesar 5. Sehingga didapatkan Hasil yang sesuai yaitu 15. serta dapat diubah-ubah X1 nya dengan re-simulate untuk mendapatkan nilai outputnya.
Tugas 2
Kami diminta untuk mengerjakan aljabar simultan dengan menggunakan variabel array di open modelica. Aljabar simultan adalah metode penyelesaian persoalan matematik yang melibatkan kekompleksan yang sangat rumit sehingga memerlukan cara penyelesaian yang membuatnya simple dengan menggunakan tools yang ada, seperti komputer dengan program visual basic, matlab atau lainnya.
beberapa metode yang terdapat pada aljabar simultan ialah :
1. metode Eliminasi Gauss
2. Metode Cramer
3. Gauss seidel
4. Gauss – jordan.
Sementara itu, variable array adalah variabel yang didalamnya memiliki beberapa data nilai. Contohnya, bila ada data X1, X2, X3 ,dan X4, makadengan menggunakan variabel array cukup dituliskan X[4] saja. Pada tugas 2 ini saya mencoba membuatnya menggunakan 3 persamaan yang sederhana dan memiliki 3 variabel yang harus dicari sebagai berikut :
function
function Gauss_Jordan input Real P[3,3]; input Real Q[3]; output Real X[3]; algorithm X:=Modelica.Math.Matrices.solve(P,Q); end Gauss_Jordan;
class
class SPL
parameter Real P[3,3]=[1,1,2;
-1,-2,3;
3,-7,4];
parameter Real
Q[3]={8,1,10};
Real X[3];
equation
X=Gauss_Jordan(P,Q);
end SPL;
Berikut adalah rekaman Video dari tugas 2:
Pertemuan Ketiga (Rabu, 25 November 2020)
Pada pertemuan ketiga kali ini diawali dengan menanyakan kabar dan juga kami diperintahkan untuk membagi/melakukan share screen terkait progress belajar metode numerik dan pemahaman tentang penggunaan OpenModelica. Kemudian dilakukan juga pembahasan tentang penggunaan OpenModelica pada permasalahan engineering. Pada permasalahan engineering, metode numerik dapat membantu menyelesaikan persoalan agar lebih cepat. Beberapa contoh metode numerik yang dapat membantu menyelesaikan permasalaha engineering diantaranya CFD(Computation fluid dynamics, Metode Stokastik, dan FEA ( FInite Element Analaysis). Tahapan untuk menyelesaikan masalah engineering menggunakan metode numerik:
- 1. Melakukan analisis terhadap masalah engineering
- 2. Melakukan pemodelan matematis dari masalah yang sudah dianalisis
- 3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer
- 4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut
Ketika kelas kami juga mendapat penjabaran menarik mengenai aljabar simultan, variable array, dan metode Gauss. Kemudian ketika sedang membahas hal ini, saudara Christo yang diminta menjelaskan hasil tugasnya pun menjelaskan terkait apa yang sudah ia buat dan kami turut mendengarkan pemaparannya sembari mencatat hal-hal tersebut. Berikut adalah code modelica untuk Gauss Jordan :
function GaussJordan
input Real [:,:] A;//matriks awal
output Real [:,:] B;//matriks tereduksi
protected
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //jumlah baris
Integer n = size(A,2); //jumlah kolom
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Baris terbawah yang mempunyai dengan pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//pindah ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Tugas 3
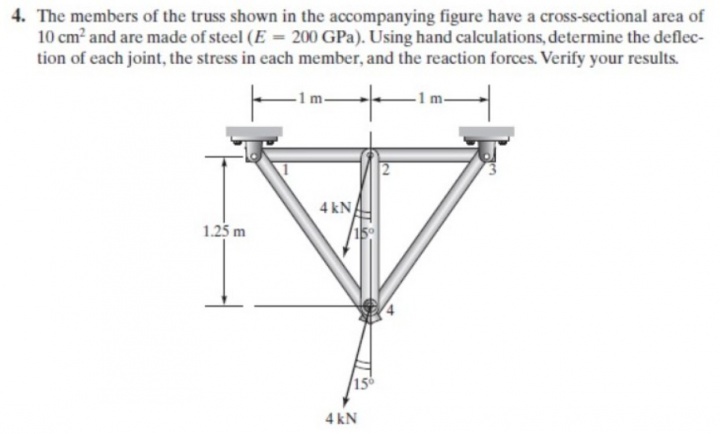
Persamaan
class TrussesTugas
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end TrussesTugas;
Transformasi Matriks
function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;Global Element Matrice
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
Reaction Matrice Equation
function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;
algorithm
X:=A*B-C;
for i in 1:N loop
if abs(X[i,1]) <= float_error then
X[i,1] := 0;
end if;
end for;
for i in 1:N loop
Sol[i]:=X[i,1];
end for;
end Reaction_Trusses;Gauss Jordan
function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;Pertemuan Keempat (Rabu, 02 Desember 2020)
Pada pertemuan keempat pada tanggal 2 Desember diawali dengan mendiskusikan terkait tugas yang diberikan pada pekan sebelumnya. Disaat teman-teman memaparkan tugas yang dibuatnya ternyata terdapat perbedaan dalam penyelesaiannya, sehingga setelah itu dibahas lebih lanjut agar dapat menemukan penyelesaian yang lebih efektif
Kuis Class Diagram dan Flowchart
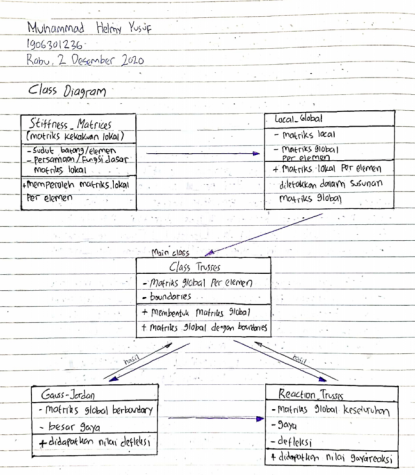
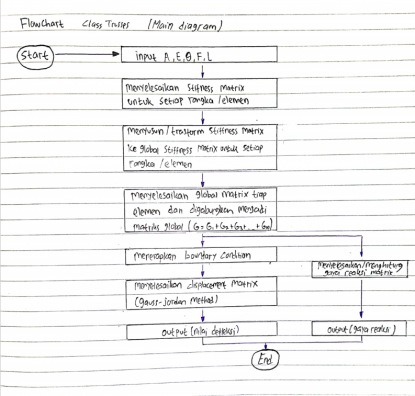
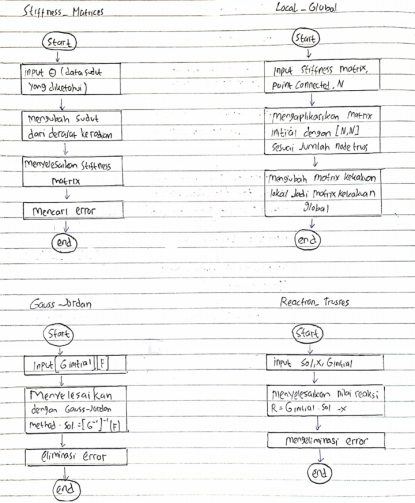
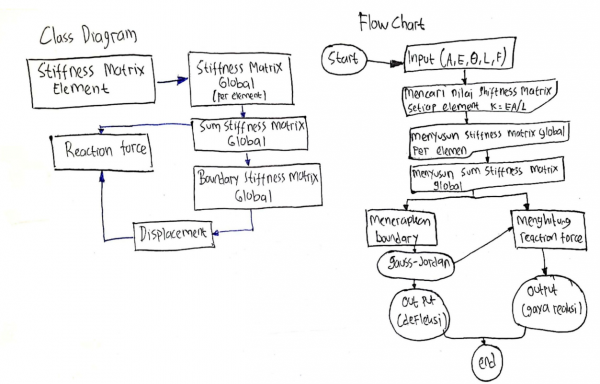
Pada pekan ke 4 kami juga diberikan kuis untuk membuat class diagram dan flowchart. kedua hal tersebut berasal dari coding penyelesaian trusses milik josiah enrico. Disini terdapat 5 coding seperti : class tusses, stiffness matrices, local global, gauss-jordan, dan reaction trusses berdasarkan yang josiah buat.
Terlebih dahulu kami diberi instruksi oleh pak dai untuk mendahulukan membuat class diagram dan dilanjutkan membuat flowchartnya.
Tugas 4
Pada PR keempat, kami diperintahkan untuk membuat class diagram, flowchart, dan coding OpenModelica
Pertama, saya membuat terlebih dahulu class diagram dan Flowchartnya sebagai berikut :
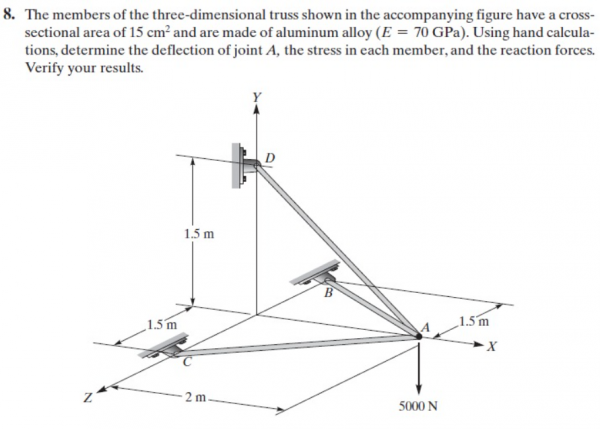
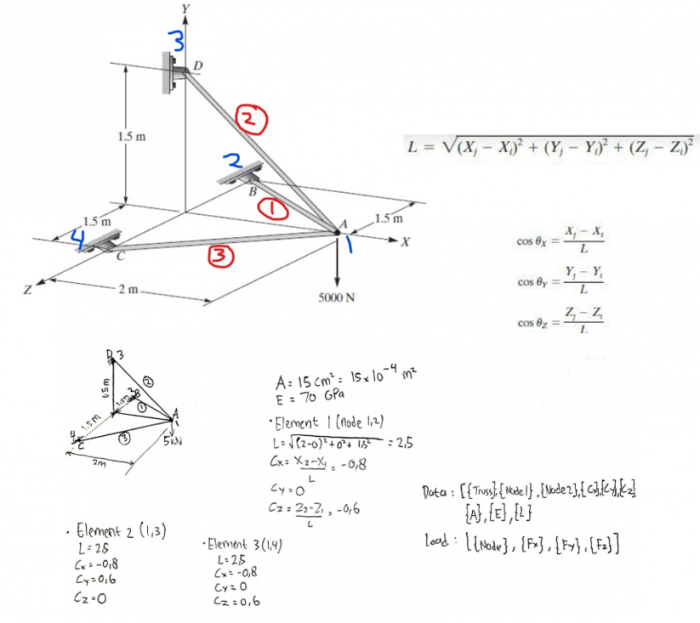
Dalam pengerjaan soal ini, saya membuat FBD terlebih dahulu untuk mencari data-data yang diperlukan, yaitu node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z.
StiffnessMatrixElement
function StiffnessMatrixElement
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
Setelah itu dibuat matriks K global 12x12 dari masing-masing element
StiffnessMatrixGlobal
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
Setelah itu semua matriks global dari masing-masing element akan dijumlahkan
SumStiffnessMatrixGlobal
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
Setelah itu tentukan juga boundaries yang ada
BoundaryStiffnessMatrixGlobal
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
Untuk mencari displacement-nya digunakan gauss jordan untuk menyelesaikan matriks
GaussJordan
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
Dan untuk melihat reaction nya digunakan code sebagai berikut :
ReactionForce.mo function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce;
Terakhir dibuat Class untuk memproses data yang sudah dibuat dan melihat hasil U dan R
Tugas4TrussNomor8
class Tugas4TrussNomor8
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end Tugas4TrussNomor8;
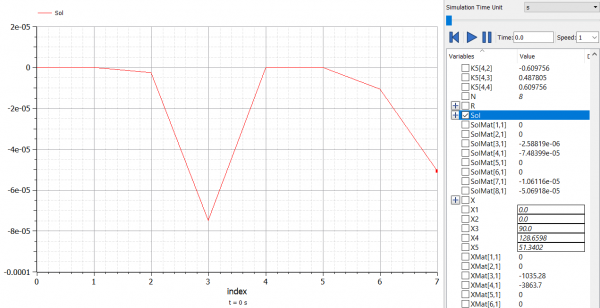
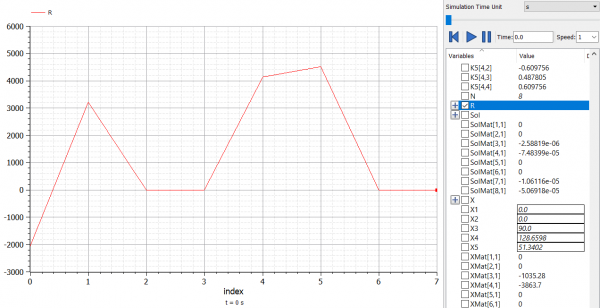
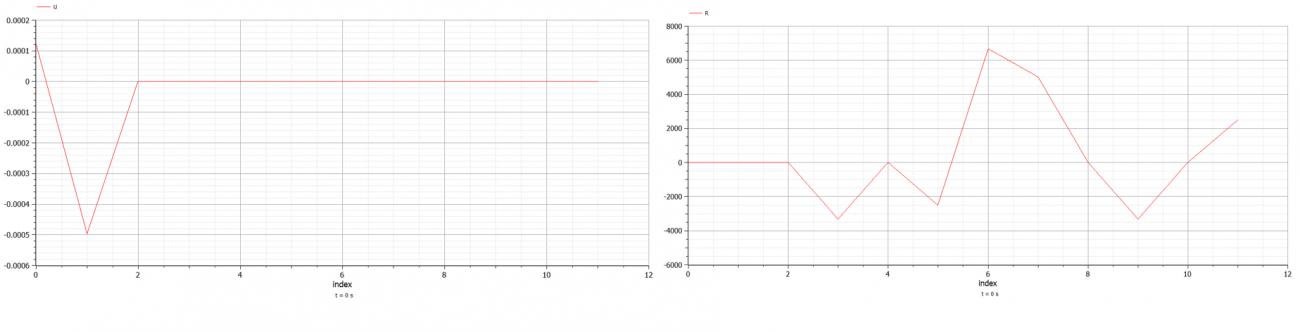
Sehingga dalam persoalan tersebut didapatkan hasil dari displacement (U) dan Reaction force (R) sebagai berikut :
berikut adalah video terkait penyelesaian 3D Truss menggunakan OpenModelica :