Oka Widiantara Suputra

Salam hangat! Selamat datang di laman saya :D

Oka Suputra

Biodata

Perkenalkan, nama saya Oka sebagai mahasiswa Teknik Mesin UI angkatan 2018. Saya bersyukur bisa mendapatkan kesempatan untuk bisa belajar dan berkembang selama 20 tahun kehidupan yang telah saya lalui. Sekilas tentang saya, berinteraksi dengan orang lain merupakan hal yang menyenangkan untuk saya karena setiap orang memiliki kisah yang unik sehingga dapat membuka wawasan ataupun perspektif. Dari situ, kita bisa menggabungkan perspektif yang ada di dunia ini sehingga didapatkan berbagai jenis cara untuk memecahkan permasalahan yang ada dan bahkan menolong orang lain. Saya percaya apabila kita ingin terus belajar, memiliki niat yang baik, berusaha, dan beribadah, pasti akan diberikan jalan yang baik untuk kedepannya.

Pertemuan-1 11/11/2020

Tujuan Pembelajaran Metode Numerik

• Memahami prinsip dasar dan konsep metode numerik sebagai bekal perjalanan kita untuk mencapai tahap selanjutnya sebagai seorang engineer

• Mampu mengerti aplikasi yang ada dalam metode numerik

• Bisa menerapkan konsep di dalam pemodelan numerik dan persoalan teknik(menyelesaikan problem dengan numerik)

• Mendapatkan nilai tambah atau value sebagai manusia yang beradab

Materi Sebelum UTS

• Pseudocode
• Sistem Persamaan
• Turunan Numerik
• Metode Newton Rhapson, Secant, Bisection
• Regresi Linear
• Interpolasi

Tugas 1

Dalam tugas yang pertama ini, saya mempelajari penggunaan Open Modelica melalui beberapa source dari youtube seperti:

• https://www.youtube.com/playlist?list=PLwpmIf9ZQ3Ex9svxIo7WrWjPESFU21oDE
• https://www.youtube.com/playlist?list=PLis_8UnILRXU3HEtRwzfGp9ESG9Hc1XKq

Setelah itu saya membuat video pembelajaran saya sendiri akan Open Modelica dengan mengaplikasikan basic nya ke dalam permasalahan Cantilever Beam

Pertemuan-2 18/11/2020

Mengapa Open Modelica?

Pada pertemuan kedua kali ini, salah satu teman saya, Yogi Gunawan memberikan suatu pertanyaan menarik kepada Pak DAI "Dari sekian program yang ada, mengapa kita memilih Open Modelica?". Kemudian Pak DAI memberikan beberapa key takeaways untuk menjawab perihal tersebut.

• Open Modelica lebih di fokuskan kepada design permodelan yang akan membantu kita, para engineers, untuk bisa menyelesaikan real case baik dari control system, heat transfer, sistem fluida dan sebagainya.
• Memudahkan kita untuk cross function (mempelajari berbagai dasar ilmu) dalam 1 software
• Open Source, berarti dia free untuk digunakan dan dapat melakukan interaksi dengan pengguna lainnya. Bahkan sekarang banyak sekali open source yang memiliki kelebihan lebih banyak dari software yang telah dilegalisasi

Tugas 2

Overview

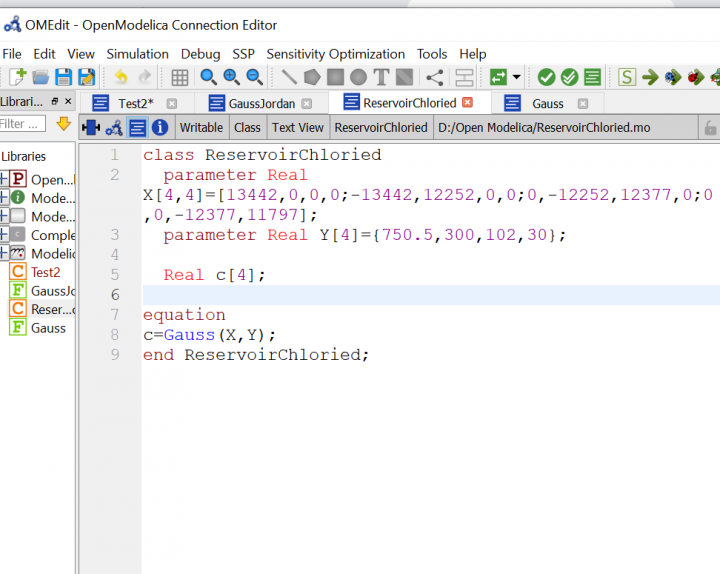
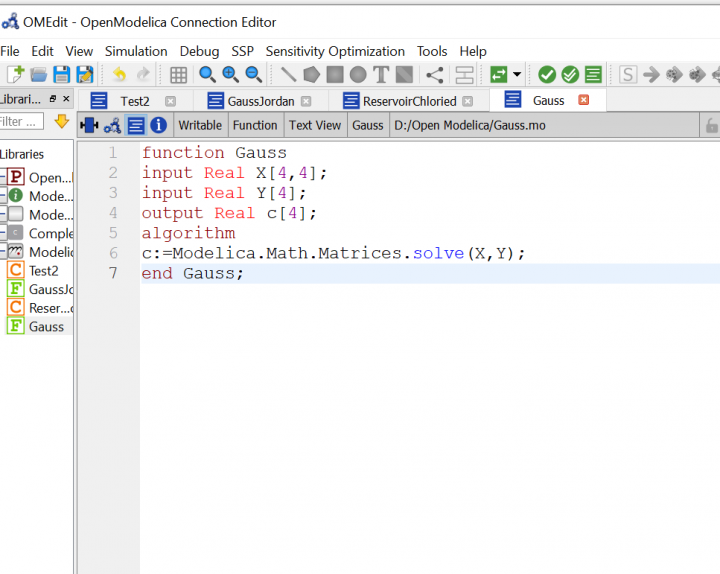
Setelah kami diajarkan oleh Pak DAI beberapa tipe modelica seperti Class dan Function, kami diberikan tugas untuk melatih implementasi tersebut ke dalam persoalan aljabar simultan.

[Aljabar Simultan merupakan metode penyelesaian persamaan matematik yang kompleks dalam satu waktu yang sama. Salah satu metode yang bisa digunakan adalah Gauss Jordan]

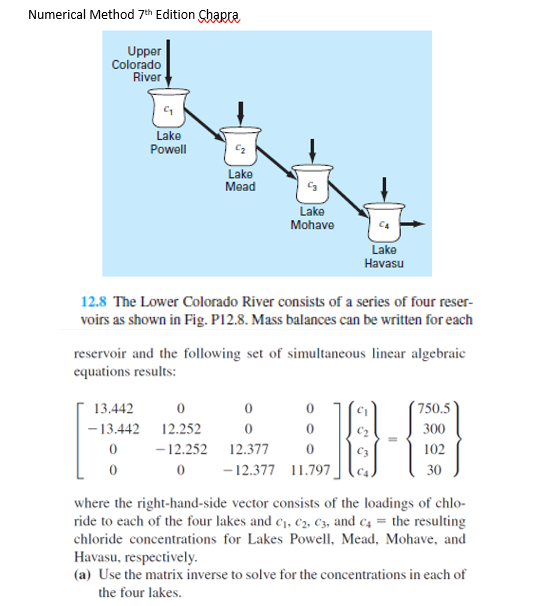
Saya mengambil contoh permasalahan dari Buku Numerical Method 7th Edition oleh Steven C. Chapra pada bab 12 problem 8 untuk dijadikan study case dalam pemrograman Open Modelica.

Pada gambar di atas, perlu diselesaikan transformasi matrix yang ada untuk bisa mendapatkan nilai c1, c2, c3, can c4 sebagai konsentrasi dari chlorida yang dibutuhkan pada masing-masing reservoir/lake. Oleh karena itu kita bisa implementasikan ke dalam Open Modelica bagian class seperti di bawah

Modelica Class

Modelica Function

Setelah disimulasi maka akan didapatkan nilai masing-masing sebagai berikut:

• c1= 0.558325
• c2= 0.857411
• c3= 0.0931163
• c4= 0.100237

Untuk mendapatkan guide secara visual, dapat dilihat di video bawah ini

Video

Pertemuan-3 25/11/2020

Materi

Pada pertemuan ini, kita mempelajari mengenai aplikasi metode numerik terhadap dunia Engineering. Adapun metode yang secara umum digunakan untuk bisa membantu kita yaitu CFD, Stokastik, dan FEA. Adapun step by step alur berpikir dalam mengerjakan sebuah engineering problem

• Masalah Teknik
• Analisis Model
• Model Matematis
• Model Numerik
• Komputer & Solusi

Gauss Jordan

Untuk materi gauss jordan ini sendiri, saya mempelajari dari Christo, teman saya yang melakukan sharing di kelas sehingga didapatkan hasil coding sebagai berikut

function GaussJordan
input Real [:,:] A;//matriks awal
output Real [:,:] B;//matriks tereduksi
protected 
Integer h = 1;    //pivot row
Integer k = 1;    //pivot coloumn
Integer m = size(A,1); //jumlah baris
Integer n = size(A,2); //jumlah kolom
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
B := A;
while h <= m and k <= n loop
 for i in 1 : m loop
   for j in 1 : n loop
    if abs(B[i,j]) <= float_error then
      B[i,j] := 0;
     end if;
   end for;
 end for;
//Finding pivot 
 pivot_column:= {B[i,h] for i in h:m};
   //Baris terbawah yang mempunyai dengan pivot tertinggi
   c:=h-1;
   for element in pivot_column loop
     c:= c+1;
     if abs(element)== max(abs(pivot_column)) then
       max_row :=c;
     end if;
   end for; 
 //Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
 if B[max_row,k] == 0 then
   k:=k+1;
 else 
   // tukar row h - max_row
   temp_array := B;
   temp_array[h] := B[max_row];
   temp_array[max_row] := B[h];
   B:= temp_array;
   //devide pivot row by pivot number
    B[h] := B[h]/B[h,k];
    for i in (h+1) :m loop
      r := B[i,k]/B[h,k];
     B[i,k]:=0;
     for j in (k+1) : n loop
       B[i,j] := B[i,j]-B[h,j] * r;
     end for;
   end for;
   //pindah ke pivot kolom dan row selanjutnya
   h := h+1;
   k := k+1;  
 end if;
 end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
 //dealing with error
 for i in 1:m loop
   for j in 1:n loop
     if abs(B[i,j]) <=float_error then
       B[i,j]:=0;
     end if;
   end for;
 end for; 
//finding pivot 
   pivot_row := {B[h,i] for i in 1:k};
   //Get position index k of pivot 
   c := 0;
   for element in pivot_row loop
     c := c+1;
     if element <> 0 then
       break;
     end if;
   end for;
   k:= c;
 // no pivot in this row, move to next row
 if B[h,k] == 0 then 
   h:= h-1;
 else
   //perform row operatation
   for i in 1:(h-1) loop
     r := B[i,k];
     B[i] := B[i] - B[h] *r;
   end for;
   //move to next pivot row dan column
   h:=h+1;
   k:=k+1;
 end if; 
end while;    
end GaussJordan;

Gauss Elimination

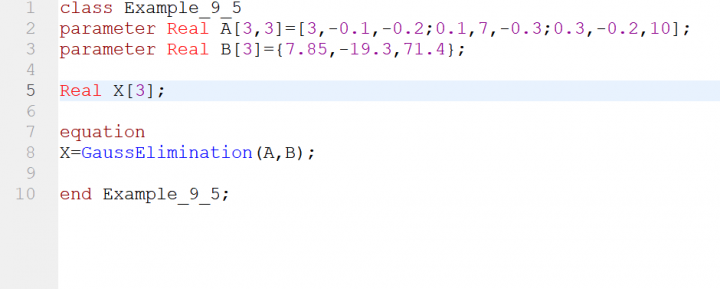
Kami mencoba mengerjakan problem pseudocode pada bagian 9.4 di buku Numerical Method 7th Edition Chapra

 function GaussElimination
 input Real [3,3] A; 
 input Real [3] B;   
 output Real [3] x;  
 protected
   Real [3,3] a;
   Real [3] b;
   Integer m = size(A,1);  // total row
   Integer n = size(A,2);  // total column
   Real k = 1;       
   Real i = 1;       
   Real j = 1;      
   Real factor = 1;   
   Real sum = 1;     

 algorithm
 a := A;
 b := B;
 // Forward Elimination
 for k in 1:(n-1) loop
 for i in (k+1):n loop
   factor := a[i,k] / a[k,k];
     for j in (k+1):n loop
      a[i,j] := a[i,j] - (factor * a[k,j]);
     end for;
     b[i] := b[i] - (factor * b[k]);
   end for;
 end for;
 // Back Substitution
 x[n] := b[n] / a[n,n];
 for i in (n-1):(-1) loop
   sum := b[i];
   for j in (i+1):n loop
     sum := sum - (a[i,j] * x[j]);
   end for;
   x[i] := sum / a[i,i];
 end for;
 end GaussElimination;

Setelah itu coding disimulasikan untuk membuktikan Example 9.5

Setelah check model dan melakukan simulasi, maka hasil dibuktikan sesuai

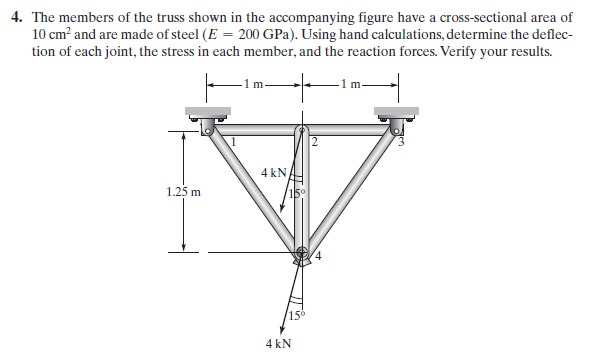
Tugas 3

Class

class TrussNo4
parameter Integer N=8; //Matrix Global dimana 2 node terhubung
parameter Real A=0.001; //Luas Penampang m^2
parameter Real E=200e9; //Modulus Young Pa
Real G[N,N]; //Global
Real Ginitial[N,N]; //Global awal
Real Sol[N]; //Displacement Global
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //Reaksi Gaya Global
Real SolMat[N,1];
Real XMat[N,1];

//boundaries
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N]; 

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

algorithm

//creating global matrice
K1:=Stiffness(X1);
G1:=k1*GlobalMatriks(K1,N,p1a,p1b);

K2:=Stiffness(X2);
G2:=k2*GlobalMatriks(K2,N,p2a,p2b);

K3:=Stiffness(X3); 
G3:=k3*GlobalMatriks(K3,N,p3a,p3b);

K4:=Stiffness(X4);
G4:=k4*GlobalMatriks(K4,N,p4a,p4b);

K5:=Stiffness(X5);
G5:=k5*GlobalMatriks(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end TrussNo4;

Function

function Stiffness
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,- Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness;

function GlobalMatriks
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
 
end GlobalMatriks;

function ReactionForce
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;
end ReactionForce;

Pertemuan-4 2/12/2020

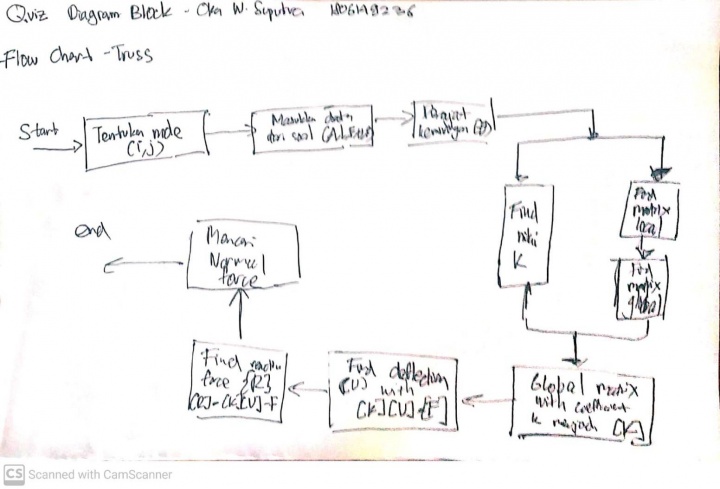
Quiz Block Diagram

Tugas 4

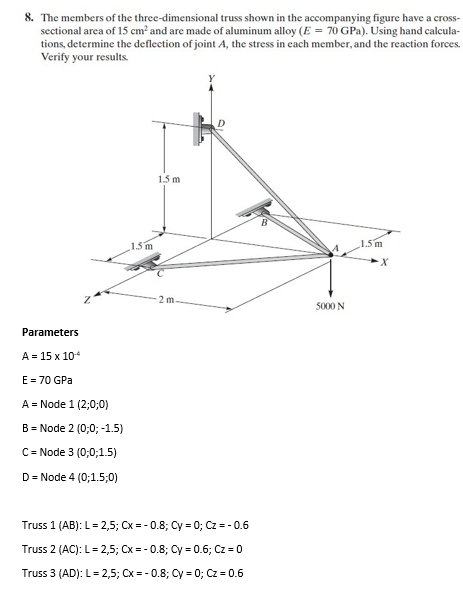
Tugas ke-4 kali ini memecahkan permasalahan Truss 3 Dimensi dengan membuat class diagram, flow chart, serta pengerjaannya di Open Modelica. Di bawah ini merupakan soal no.8 yang akan dipecahkan serta sudah di breakdown beberapa parameter yang ada secara manual

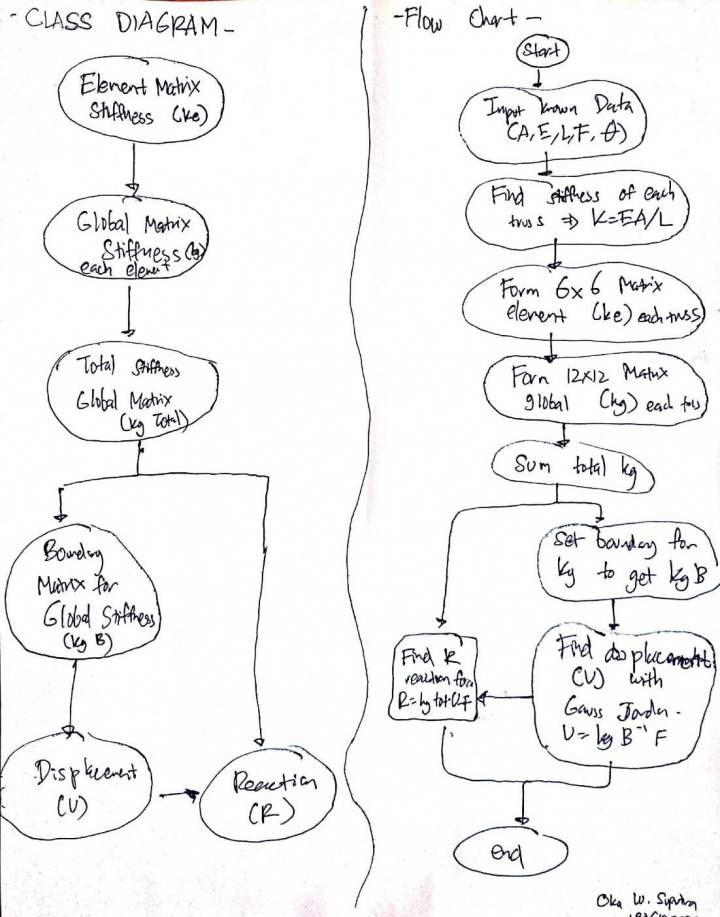
Setelah itu dibuat class diagram dan flow chart di bawah sebagai berikut

Kemudian dengan referensi code dari ananda Mohammad Fahmi

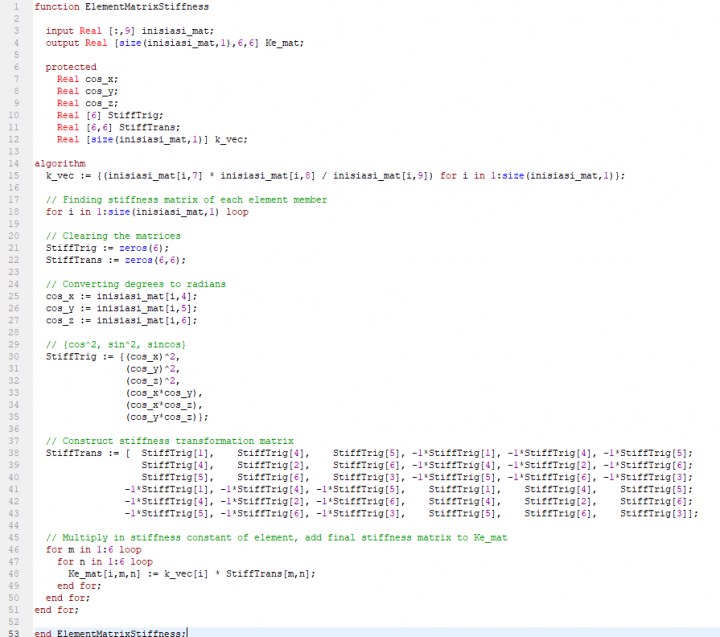
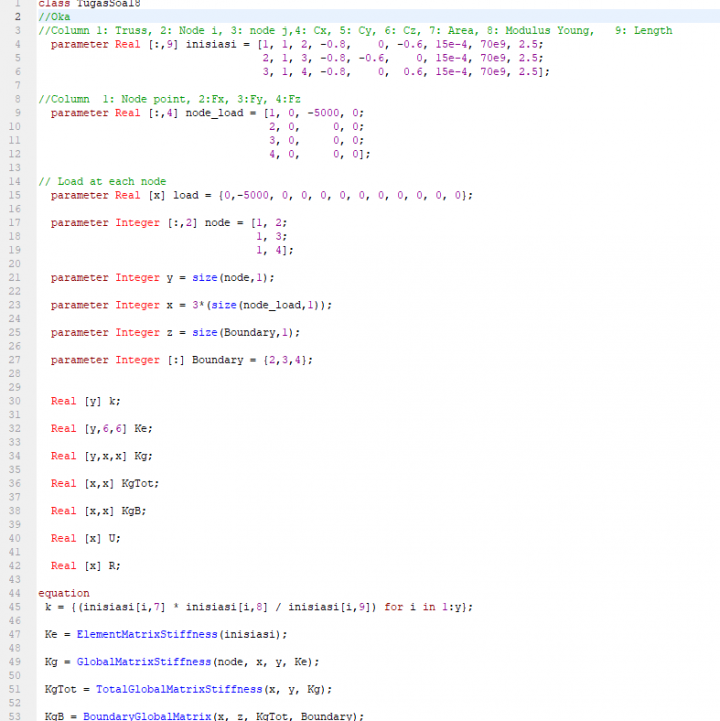
• 1st step yang akan dilakukan yaitu mencari k dengan rumus k=AE/L yang akan digunakan untuk forming matriks stiffness elemental (Ke) pada setiap truss

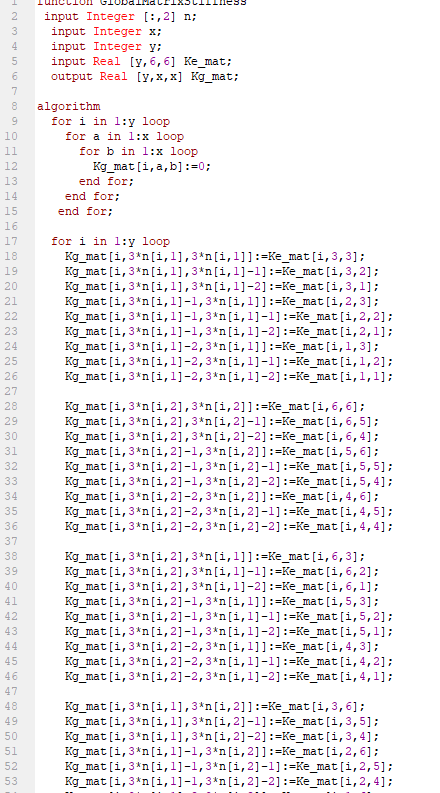
• 2nd step yaitu mentransfer matrix element 6x6 menjadi matrix global 12x12 untuk forming matriks stiffness global (Kg) yang disesuaikan dengan jumlah truss (3) dikali dengan jumlah node (4)

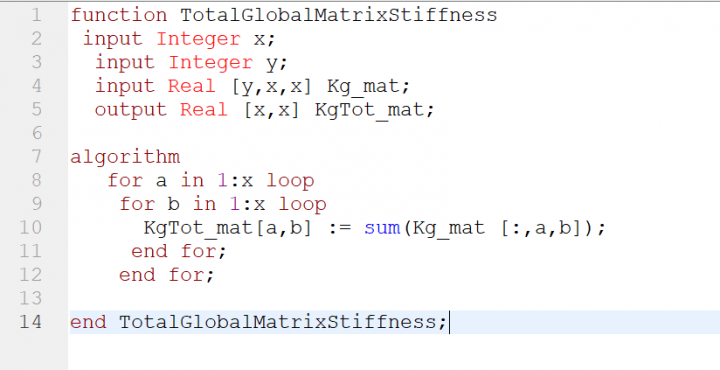
• 3rd step yaitu menjumlahkan semua matriks stiffness global pada setiap truss menjadi sum of matriks stifness global (Kgtot)

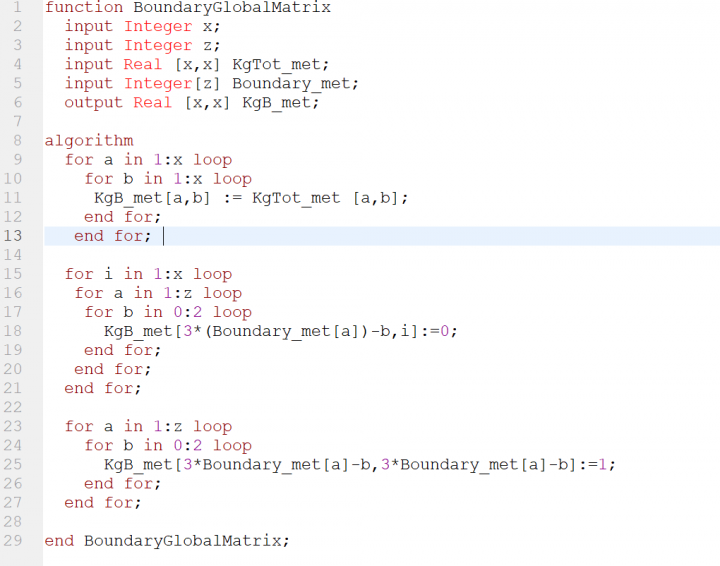
• 4th step yaitu menetapkan boundaries pada sum of matriks stifness global menjadi (KgB), dimana kasusnya setiap node berupa tumpuan pinned

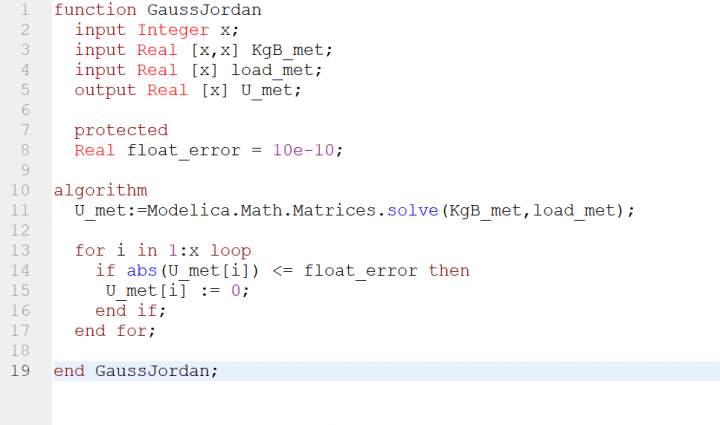
• 5th step yaitu mencari displacement (U) dari masing-masing titik matrix, dengan equation XU=F, dimana X adalah KGB, U merupakan displacement, dan F adalah Gaya Eksternal. Untuk bisa mendapatkan nilai U maka dilakukan fungsi Gauss Jordan

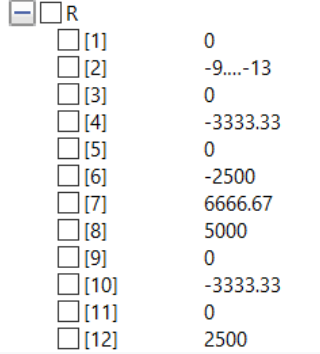
• 6th step yaitu mencari gaya reaksi (R) dengan persamaan R=Kg*U - f yang dimasukan ke dalam function

• 7th step yaitu membuat Class yang diinput data-datanya dari parameter soal kemudian dipanggil semua fungsi yang ada untuk mendapatkan nilai yang dicari

• 8th step yaitu melakukan simulasi sehingga mendapatkan U dan R

Untuk video penjelasan ada di bawah ini:

720px