Muhammad Afif Rachmat

From ccitonlinewiki
Revision as of 15:32, 9 December 2020 by Mafifrachmat (talk | contribs) (→‎Minggu Ke empat (2 Desember 2020))
Jump to: navigation, search
Biodata
Center
Nama Muhammad Afif Rachmat
NPM 1906356185
Email Muhammad.afif92@ui.ac.id
Youtube https://www.youtube.com/watch?v=szu4bZKi0Vw


Muhammad Afif Rachmat

Biodata Nama : Muhammad Afif Rachmat TTL  : Lebak, 08 April 2001 Jurusan : Teknik Mesin Hobi : games, catur, outdoor


HALO! Perkenalkan nama saya Muhammad Afif Rachmat (NPM 1906356185) biasa dipanggil Afif. Saya Adalah mahasiswa Teknik Mesin angkatan 2019 dari Fakultas Teknik Universitas Indonesia. Seaya memiliki ketertarikan kepada bidang mesin karena saya ingin berinovasi dan berkreasi di bidang teknologi seperti Alm. B.J. Habibie. untuk itu saya memasuki jurusan mesin untuk mengejar cita-cits saya.

Materi Sebelum UTS

Sebelum UTS kami diajarkan oleh Bapak Engkos A. Kosasih, dan materi yang diajarkan diantaranya adalah:

  • Deret Mclaurin & Deret Taylor, dengan metode forward, center, dan backward
  • Bracketing Methods dan Open Methods, dimana bracketing methods meliputi graphical methods, bisection methods, dan false-position methods sedangkan open methods meliputi simple fixed-point iteration, newton-raphson methods, secant methods, dan brents methods
  • Mencari nilai interpolasi dan regresi linier menggunakan matriks

Catatan Minggu Pertama (11 November 2020)

Tujuan Pembelajaran

  • Memahami konsep dan prinsip dasar metode numerik
  • Dapat menerapkan pemahaman yang didapatkan dalam mata kuliah Metode Numerik
  • Mampu menerapkan pemahaman metode numerik dalam bidang keteknikan
  • Membentuk kita menjadi orang yang lebih beradab

Manfaat Belajar bagi Diri Saya Sendiri

Menurut saya, pembelajaran adalah suatu proses untuk memahami peristiwa-peristiwa yang terjadi di sekitar kita. Saya merasakan bahwa dengan belajar, saya dapat lebih memahami tentang peristiwa-peristiwa yang terjadi di lingkungan saya, dan membantu saya untuk memecahkan permasalahan baru yang sebelumnya belum pernah saya temukan. Belajar juga dapat meningkatkan kepekaan sosial, kepedulian dan empati dalam diri saya.

Komputer dalam Metode Numerik

Komputer merupakan alat hitung yang sangat cepat, namun pada hakikatnya, komputer bersifat "dummy" dan mempunyai batasan-batasan hitungan yang tidak dapat dilewati. Apa artinya bagi diri saya adalah saya menyadari bahwa komputer merupakan alat hitung yang cepat, namun pada akhirnya semuanya bergantung kepada sang pengguna itu sendiri, sehingga kita harus bisa lebih percaya diri dan menyadari bahwa kemampuan kita bahkan lebih diatas komputer manapun.

Tugas Minggu Pertama

Dalam kesempatan kali ini saya membuat suatu video pembelajaran mengenai penggunaan aplikasi OpenModelica pada perhitungan gaya dalam Katrol Majemuk :

Catatan Minggu Kedua (18 N0vember 2020)

    Pada Minggu kedua ini Mahasiswa harus sudah mengerjakan tugas yang diberikan oleh dosen dan bisa menjelaskannya .Sebelum memasuki materi pembelajaran metode numerik, Mahasiswa diminta mereview fungsi pembelajaran aljabar linear dan hubungannya dengan metode numerik. Kemudian, menceritakan pengalaman mempelajari aplikasi Open Modelica. Dan dari yang saya pelajari, aplikasi ini dibuat dengan tujuan bahasa pemodelan, bukan coding. Namun, ketika melakukan perhitungan, code yang ditulis harus dalam bahsa C++. Salah satu alasan pemilihan penggunaan aplikasi ini adalah karena Open Modelica dibuat open dan free, yang dimana semua orang boleh menggunakannya. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, connector, expanable connector, record, function, dan lain-lain. Aplikasi ini object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya ke dalam satu model, dengan pembelajaran hari dapat disebut sebagai sistem panggil.

Tugas Minggu Kedua

berikut adalah tugas untuk minggu kedua yaitu tentang class dan cara memanggil function.

Catatan Minggu Ketiga (25 November 2020)

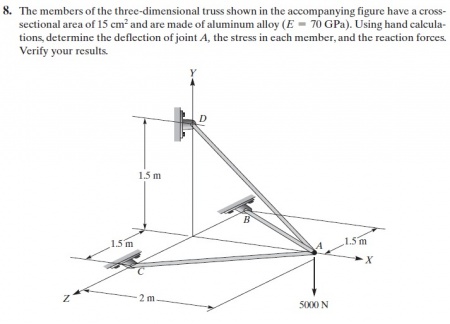
Pada minggu ketiga ini kami diminta untuk membuat pseudocode untuk metode penyelesaian Gauss-Jordan. namun pada kelas, masih banyak mahasiswa termasuk saya yang sudah lupa dan tidak bisa membuat pseudocode untuk Gauss-Jordan. jadi untuk minggu ketiga ini mahasiswa harus melakukan latihan yang ada di buku finite element dan mencoba menyelesaikan persamaan pada 9.5 di OpenModelica.

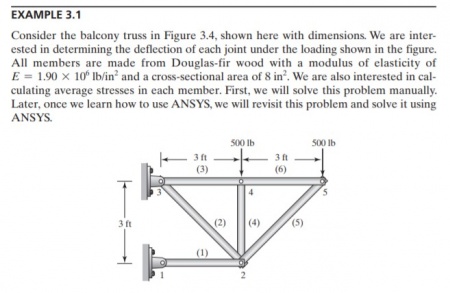
tugas tentang trusses

Soal Trusses 1 fashal.jpg

We can use Finete Element Method to solve this problem. We can make equation with numerical method use Open modelica.

Persamaan 

model Trusses

parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary coundition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];

//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);

G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses;

Stiffness Matricies 

function Stiffness_Matrices

input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
protected
final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
   
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); 

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;


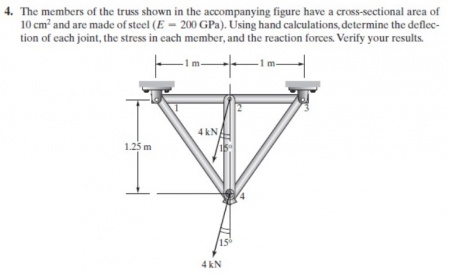
Trusses Problem 2 (Homework)

Soal Trusses 2 fashal.jpg


Discplacement Graphics
Reaction Forces Graphics

Persamaan 

class Trusses_HW

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_HW;

Fungsi Panggil

Matrice Transformation 

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice 

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Gauss_Jordan 

function Gauss_Jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;

algorithm
X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop
  if abs(X[i]) <= float_error then
    X[i] := 0;
  end if;
end for;

end Gauss_Jordan;

Reaction Matrice Equation 

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;


Minggu Ke empat (2 Desember 2020)

Pada pertemuan ke empat ini mahasiswa harus melaporkan hasil pekerjaan rmah yang diberikan selama seminggu terakhir untuk di koreksi. pada pertengahan kelas didapati bahwa model pseudocode yang paling baik adalah yang josiah dan ka Hikaru. kemudian mahasiswa harus mengkaji ulang dan mengevaluasi pekerjaan rumah untuk menjadi seperti josiah atau ka Hikaru. dan di akhir pertemuah, diberikan Quiz untuk membuat diagram kelas dan flowchart dari modelica yang sudah diprogram oleh josiah. ditambah dengan PR 4 untuk membuat flowchart dan diagram kelas pada soal trusses yang diberikan.

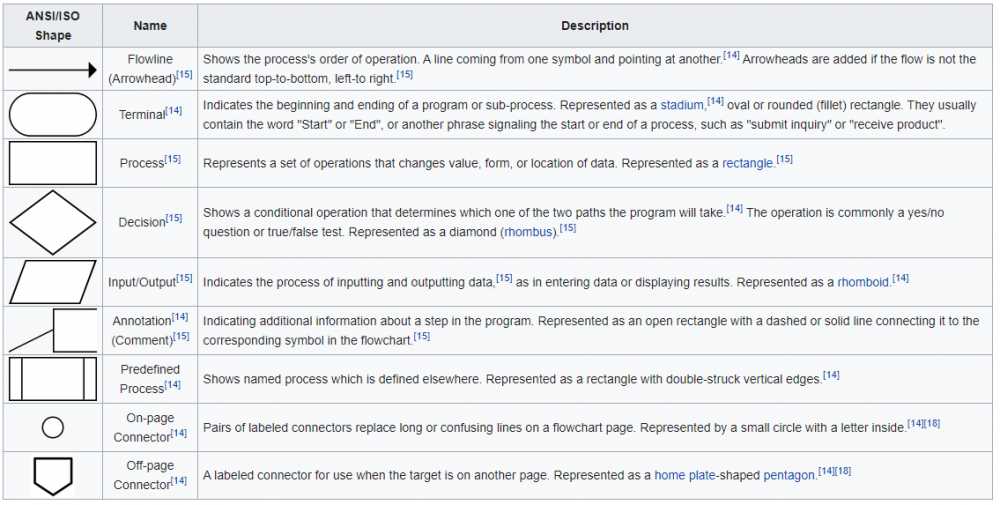
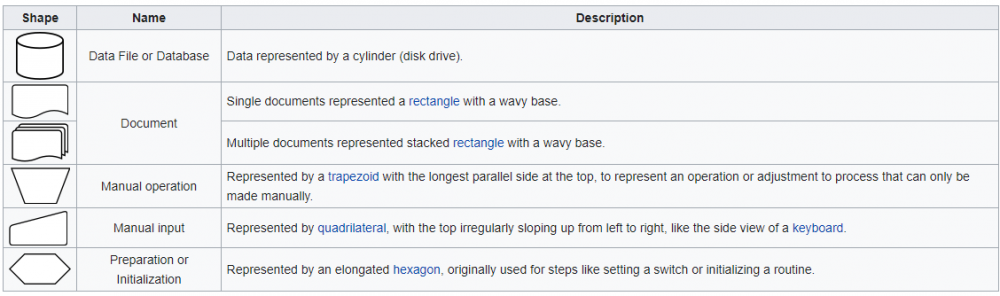
flowchart adalah alur pengerjaan atau sebuah peta konsep untuk mempermudah penjelasan mengenai penyelesaian suatu sistem. Didalam flowchart terdapat diagram kelas untuk melambangkan apa yang harus dilakukan atau yang terjadi kepada sistem tersebut selama berada di bagian itu. berikut adalah jenis-jenis diagram kelas untuk melambangkan suatu kerja.

    • RichardoWeek41.png
    • RichardoWeek42.png


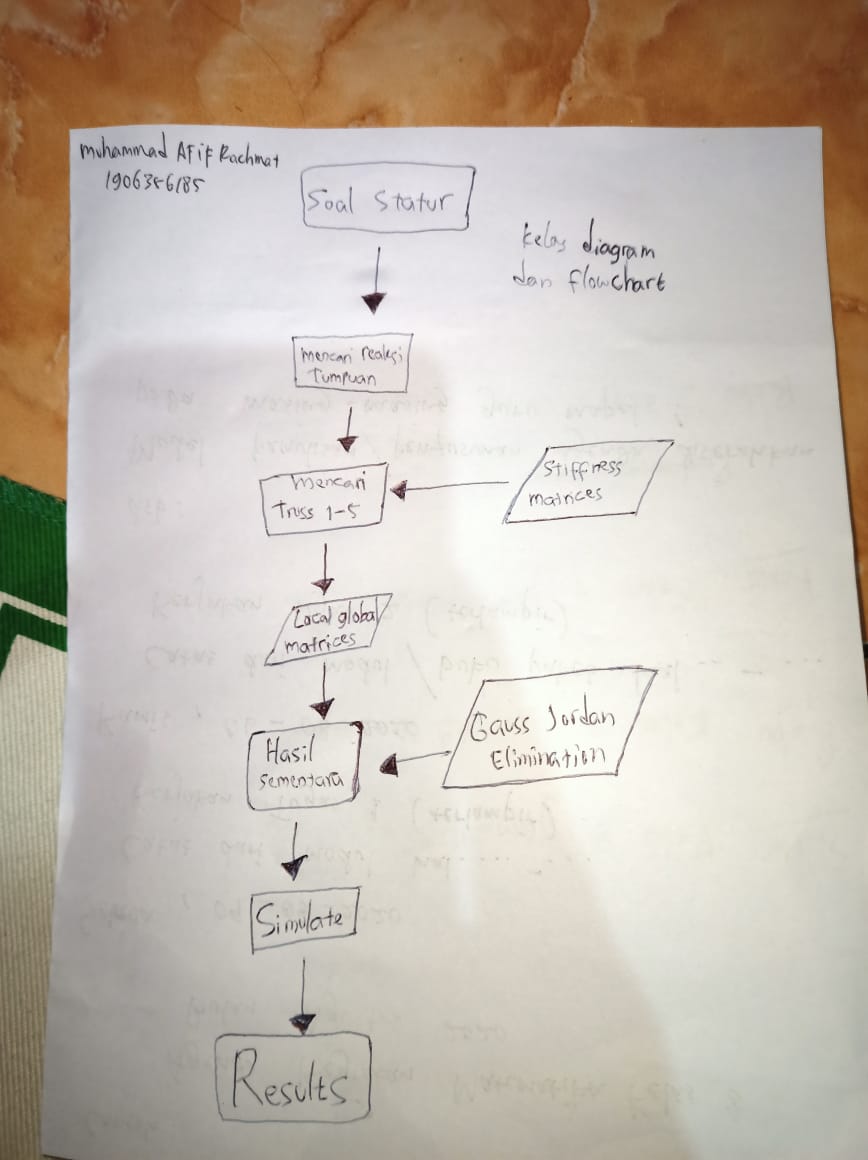
Quiz Flowchart and Diagram Class

Pada Quiz pertama saya mencoba membuat flowchart dan diagram class sendiri untuk menaksir alur pengerjaan modelica josiah, berikut adalah hasil yang saya buat sendiri berdasarkan perkiraan saya:


Qz1.jpeg

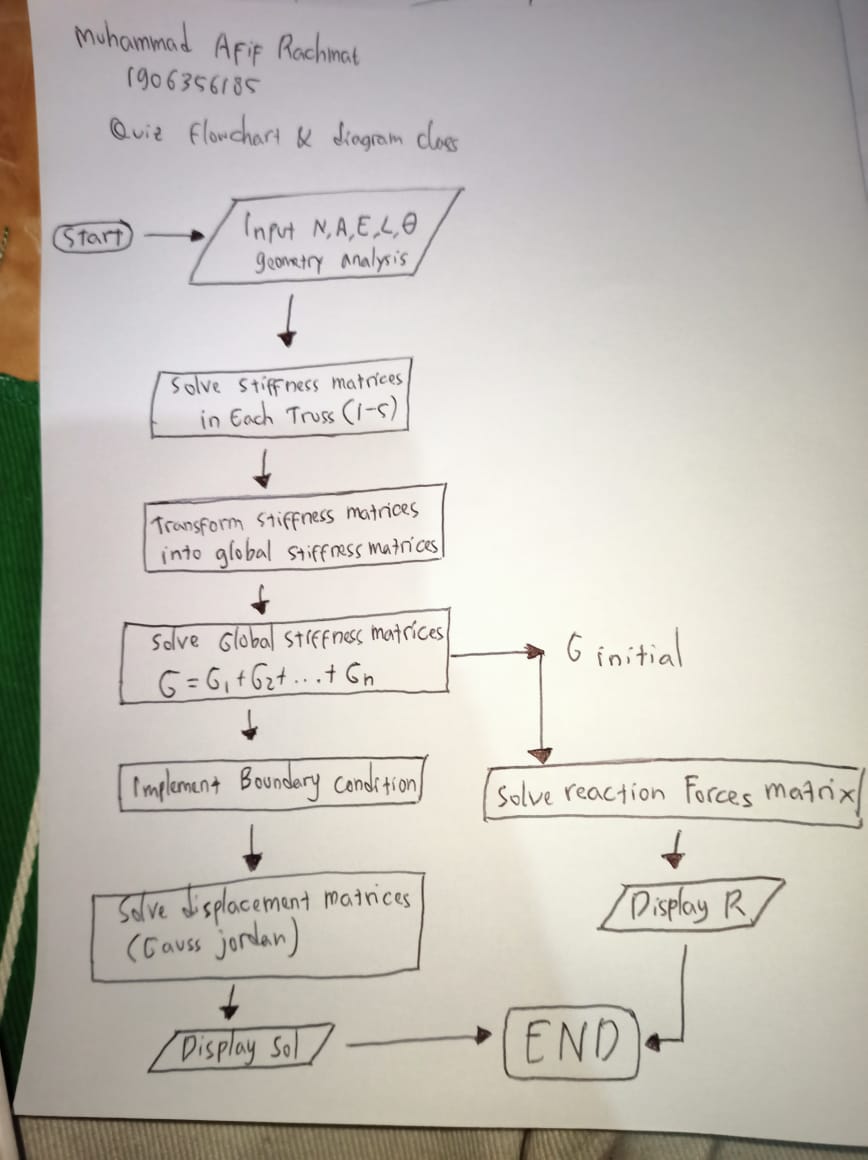
Kemudian Setelah beberapa saat berdiskusi, akhirnya diperlihatkan bahwa flowchart josiah lebih baik dan lebih lengkap. sehingga semua mahasiswa harus merevisi hasil pengerjaannya masing-masing agar menjadi seperti josiah. berikut adalah flowchart hasil revisi saya berdasarkan flowchart josiah.


Qz2.jpeg

Tugas Minggu keempatt

Mebuat flow chart diagram class dan coding open modelica

Tr 1.jpeg


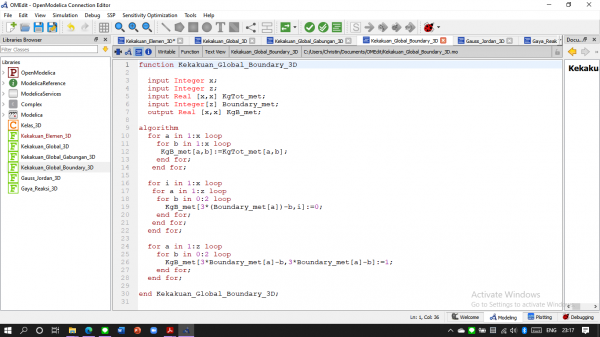
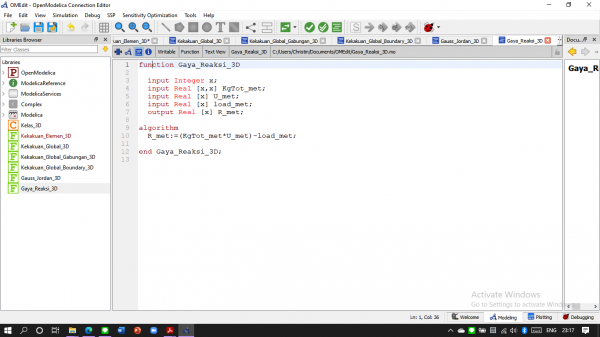
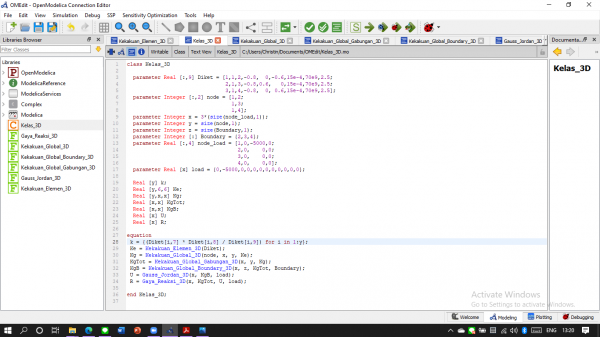
Dibawah ini adalah coding untuk soal 3d trusses berdasarkan dari saudara Ahmad Mohammad Fahmi dari kelas metode numerik 03 :

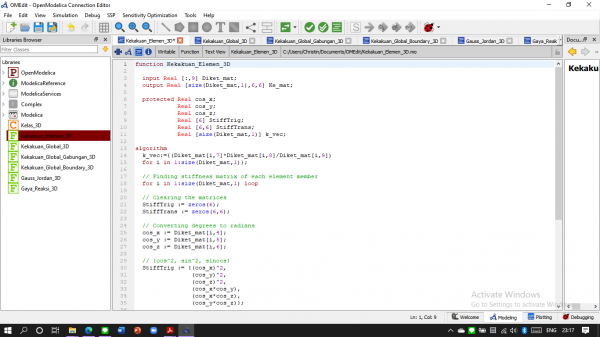
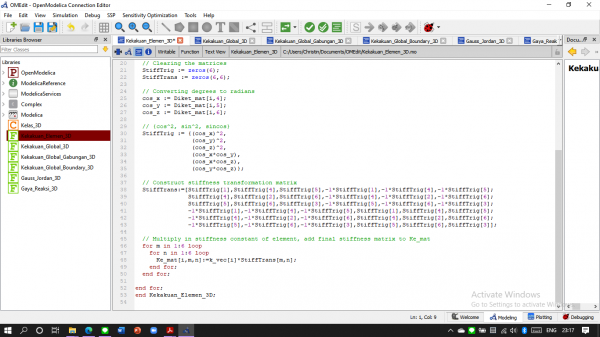
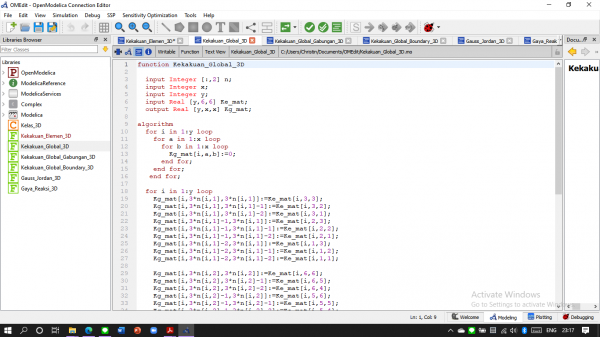
Membuat Kekakuan elemen

KE 3D 1.png
KE 3D 2.png


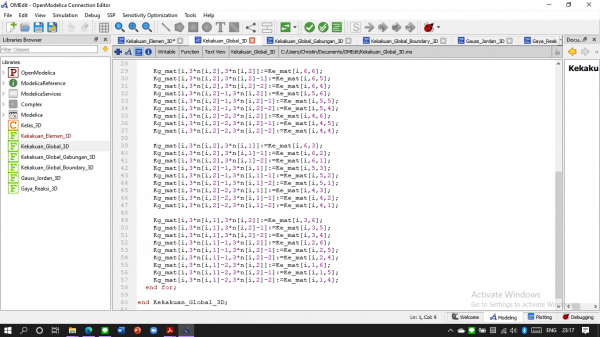
Membuat Kekakuan Global

KG 3D 1.png
KG 3D 2.png


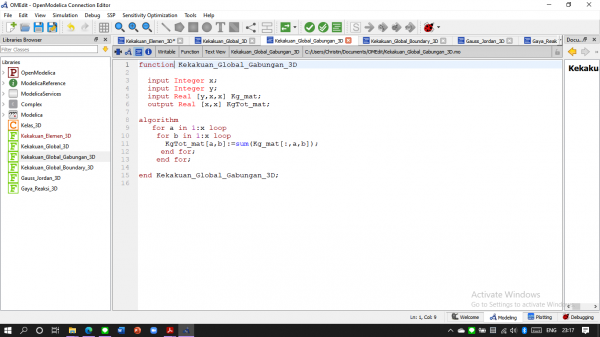
Membuat Kekakuan Global Gabungan (hasil penjumlahan kekakuan global per elemen)

KGG 3D.png
KGB 3D.png


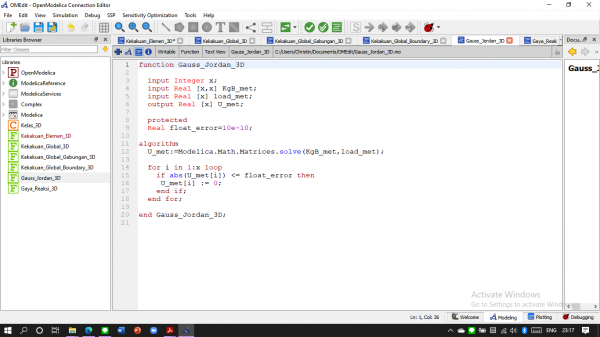
Membuat Gauss Jordan

Gauss Jordan 3D.png


Membuat Gaya Reaksi

Gaya Reaksi 3D.png


Membuat Kelas Pemanggil

Kelas 3D.png

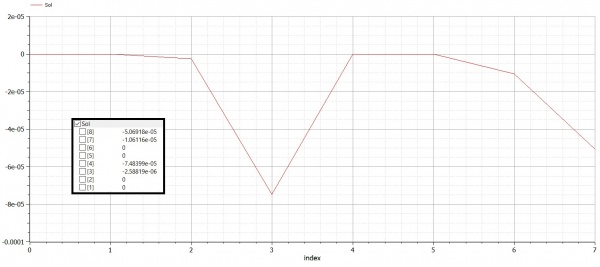
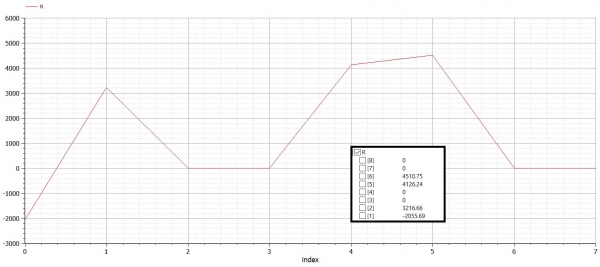
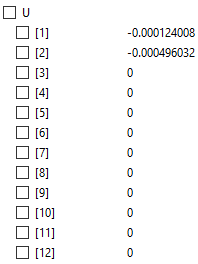
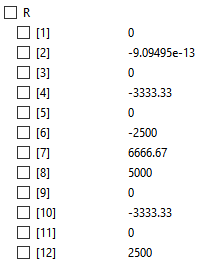
Setelah itu didapatlah hasil untuk U (defleksi) dan R (gaya reaksi)

U 3D.png R 3D.png

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Muhammad_Afif_Rachmat&oldid=47685"