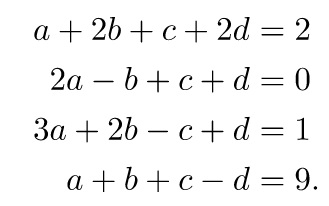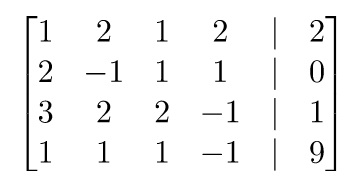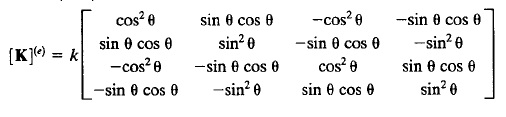Metnum03-Muhammad Rizza Fachri Nugraha
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
segala puji bagi Allah SWT dan sholawat serta salam kepada Nabi Muhammad SAW
Contents
BIODATA
Nama : Muhammad Rizza Fachri Nugraha
NPM : 1906435536
e-mail : mrizzafachri@gmail.com
Pendidikan Terakhir : Diploma
TUGAS 1
Pada tugas kali ini saya ingin menyelesaikan kasus mengenai perhitungan penurunan RPM pada setiap pergantian gigi pada sepeda motor, diketahui rasio gigi setiap gigi dengan asumsi pergantian gigi pada 10.500 rpm.
Dengan data rasio gigi :
1th 33/11
2nd 29/15
3rd 26/18
4th 28/23
5th 23/22
6th 24/26
Rumus-rumus yang saya gunakan :
Rumus presentase RPM drop saat pergantian gigi = (rasio gigi ke(n)-rasio gigi ke(n+1))/(rasio ke(n)) x 100%=a
Rumus penurunan RPM saat pergantian gigi = Presentase drop x RPM saat pergantian gigi=b
Rumus RPM setelah pergantian gigi= RPM saat pergantian gigi-Penurunan RPM saat pergantian gigii=c
berikut link pengerjaan saya : https://www.youtube.com/watch?v=DGQd7fZMoa0
Pertemuan ke-2, 16 November 2020
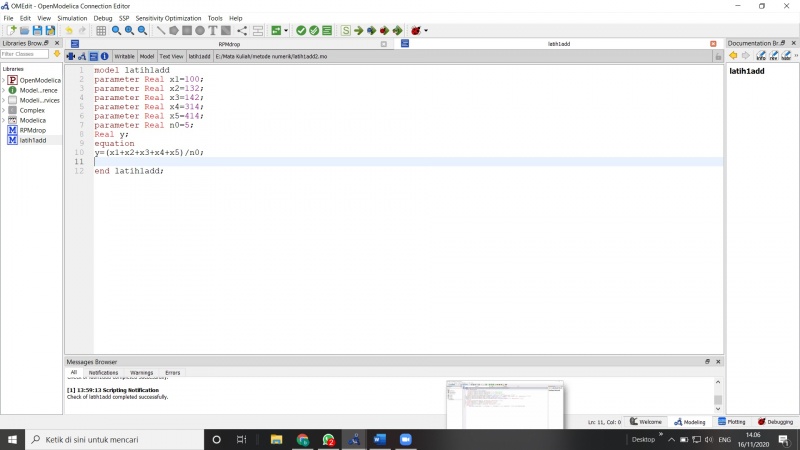
Pada pertemuan kali ini saya mencoba mencari rata-rata dari sejumlah data yaitu 100,132,142,314,414 dengan jumlah data sebanyak 5.
Untuk nilai parameter real yang saya masukan yaitu nilai yang diketahui berupa data-data tersebut seperti 100,132,142,314,414 dengan jumlah data sebanyak 5.
Variable-variable yang diketahui : x1 = 100 x2 = 132 x3 = 142 x4 = 314 x5 = 414 n = 5
Untuk variable real ditujukan untuk mencari hasil dari perhitungan yang telah kita masukan equationnya berupa rumus rata-rata.
RUMUS RATA-RATA = (JUMLAH DATA/BANYAK DATA)
bisa dilihat dibawah coding nya
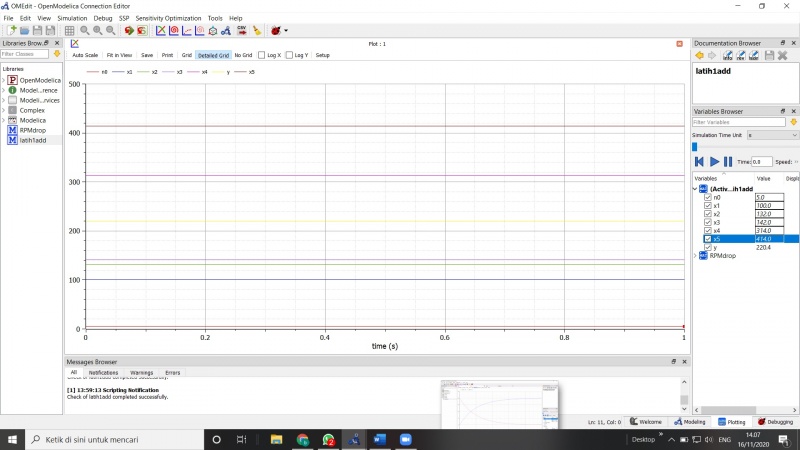
dan hasil ploting nya
Bisa kita lihat padaa Variable browser hasil perhitungan berupa variable "y" dengan nilai 220.40
TUGAS 2
Penyelesaian persoalan Aljabar simultan menggunakan software OpenModelica.
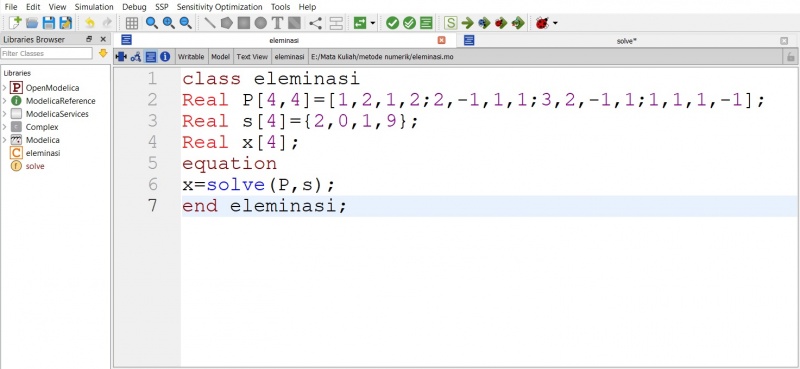
Persoalan yang saya pilih berupa Eleminasi Gauss, dengan soal :
Persamaan diatas dirubah terlebih dahulu menjadi matriks agar parameter-parameternya dapat dimasukkan pada OpenModelica.
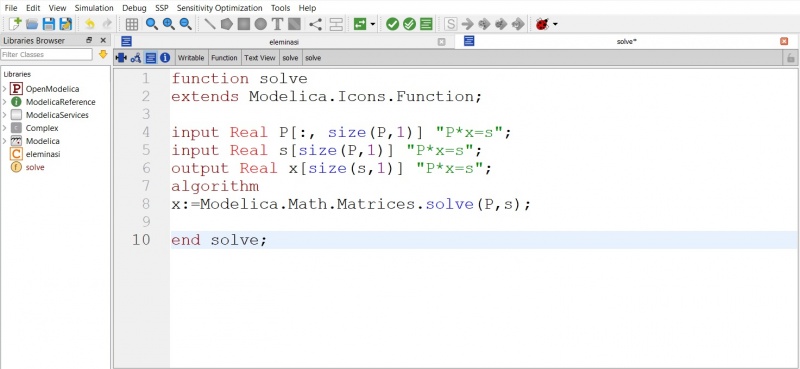
Saya menggunakan Modelica class dengan spelization "function" dan "class"
Saya menggunakan Modelica.Math.Matrices.solve(Matriks,vektor) untuk menyelesaikan persoalan tersebut dengan memanggil fungsi tersebut ke halaman class.
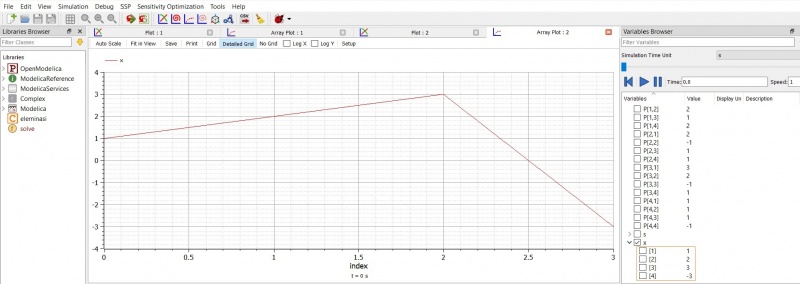
Setelah di check dan benar, dan dilakukan simulasi, didapat hasil sebagai berikut :
Bisa dilihat hasil pada kotak berwarna orange dimana berurut dari atas ke bawah, a = 1 ; b = 2 ; c = 3 ; d = -3 .
Pertemuan ke-3, 16 November 2020
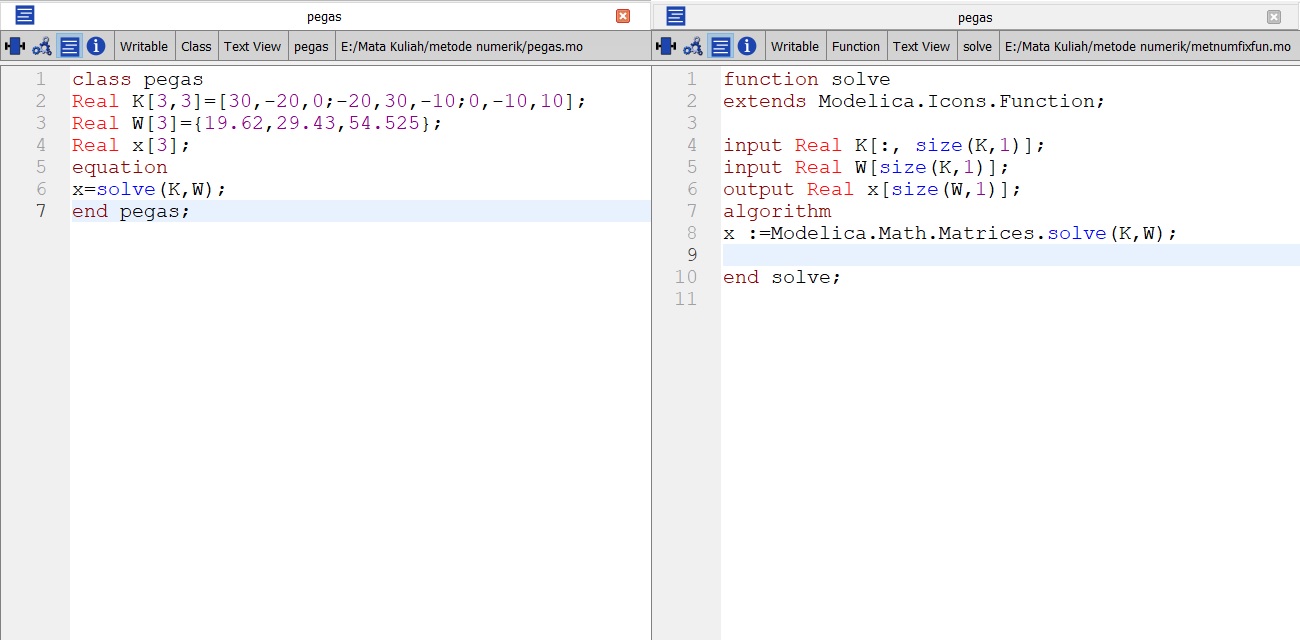
Pada pertemuam ke-3, diberikan latihan dari buku Metode Numerik edisi ke 7 karangan Steven C.Chapra dan Raymond P.Canel pada hal 328 latihan 12.11.
Persamaan yang telah didapat dari kasus
3.K.X1-2.K.X2=m1.g -2.k.X1+3.K.X2-K.X3=m2.g -K.X2+K.X3=m3.g
Penyelesaian menggunakan Open modelica
Hasil Plot
Setelah mencocokan jawaban dengan hasil manual, tidak terdapat perbedaan secara signifikan hanya berbeda pada pembulatan.
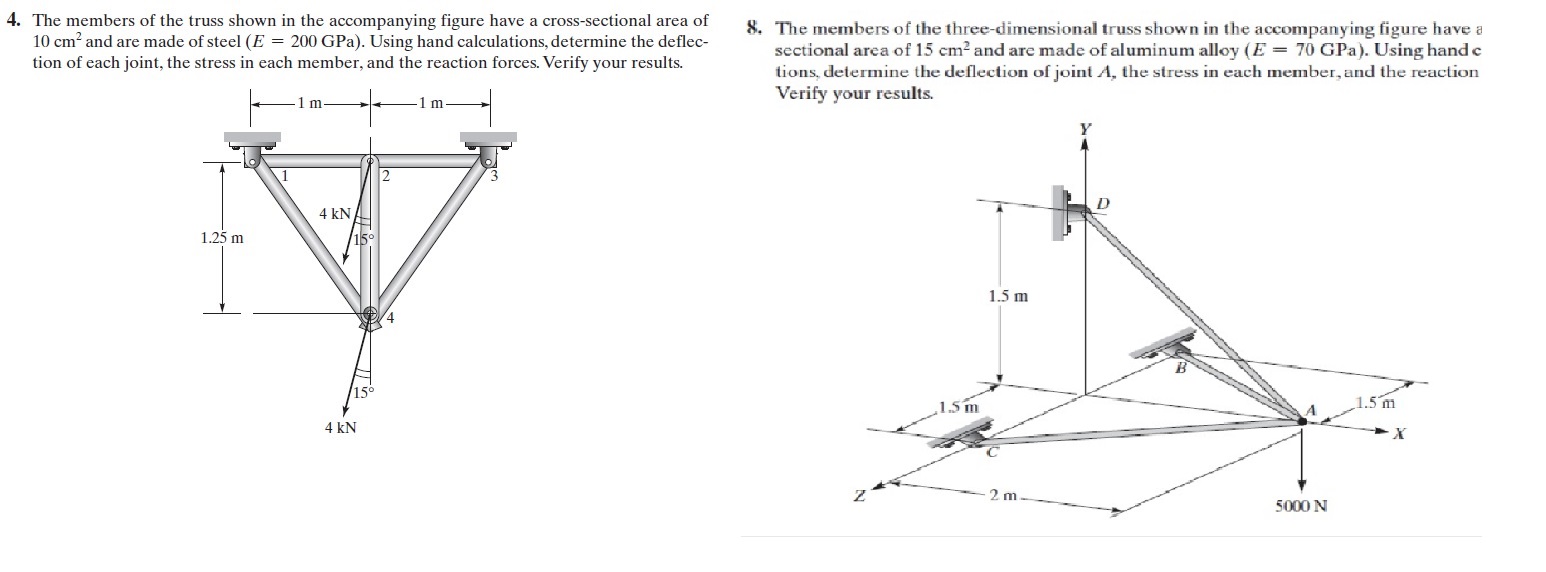
TUGAS 3
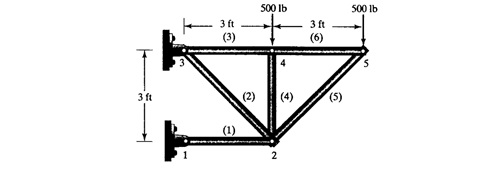
Menghitung defleksi pada setiap batang dan gaya reaksinya.
- Hubungan antara elemen dan nodes.
bisa dilihat pada gambar dimana elemen sebagai batang dan node sebagai tumpuan.
Seperti elemen 1 dengan node 1 dan 2, dst. Penentuan I dan J berdasarkan urutan angka.
- Menentukan nilai konstanta kekakuan constant dari setiap elemen.
Elemen horizontal (1,3,4,6)
k = AE/L = (8 [in^2]).(1.9x106 [lb/in^2]) / 36 in = 4.22x105 [lb/in] Elemen miring (2,4) mempunyai L = 36 [in]/cos(45) = 50.9 in
k = AE/L = (8 [in^2]).(1.9x106 [lb/in^2]) / 50.9 in = 2.98x105 [lb/in]
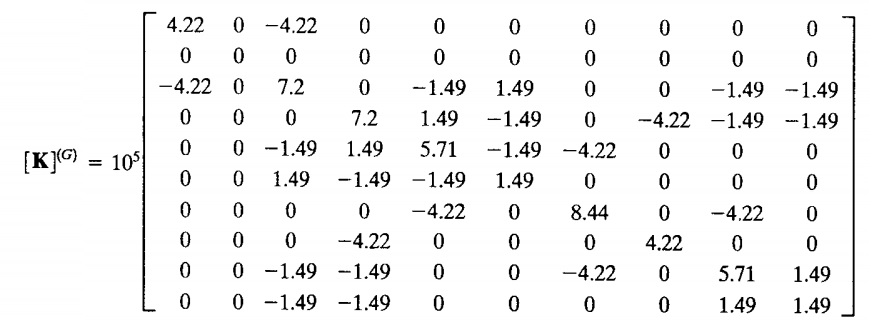
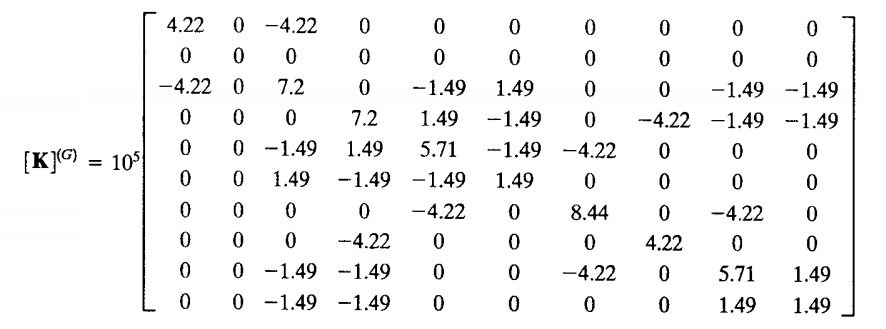
- Matrix Global untuk nilai K.
Dimana untuk mencari K^(G)=K^(1G),K^(2G),K^(3G),K^(4G),K^(5G), dan K^(6G) digunakan matriks sebagai berikut.
maka didapat hasil dari matriks global sebagai
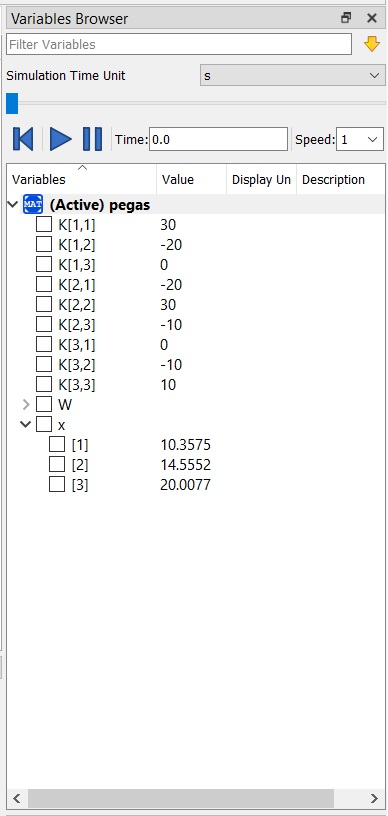
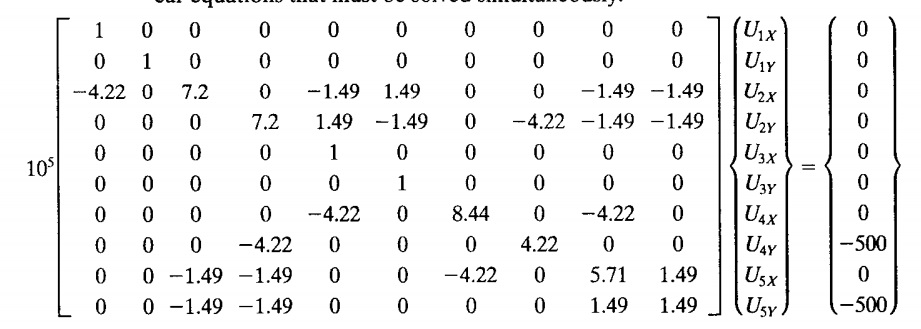
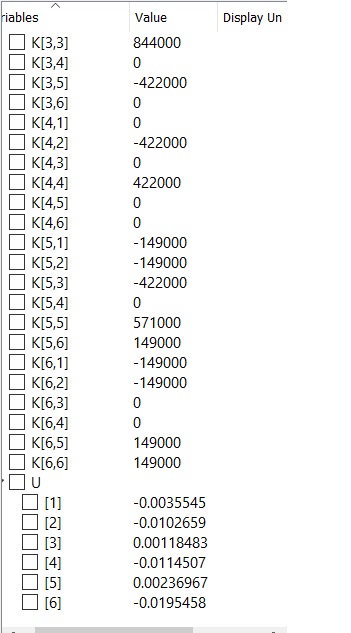
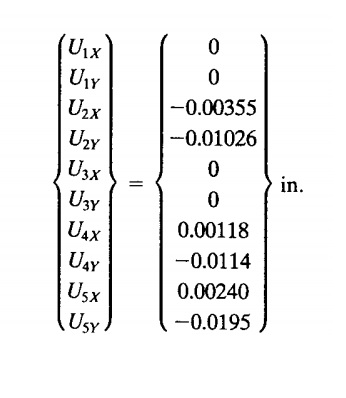
- mencari nilai U
Karena pada node 1 dan node 3 elemen berupa fixed, maka U1x,U1y,U3x,U3y = 0.
disederhanakan menjadi matriks 6x6
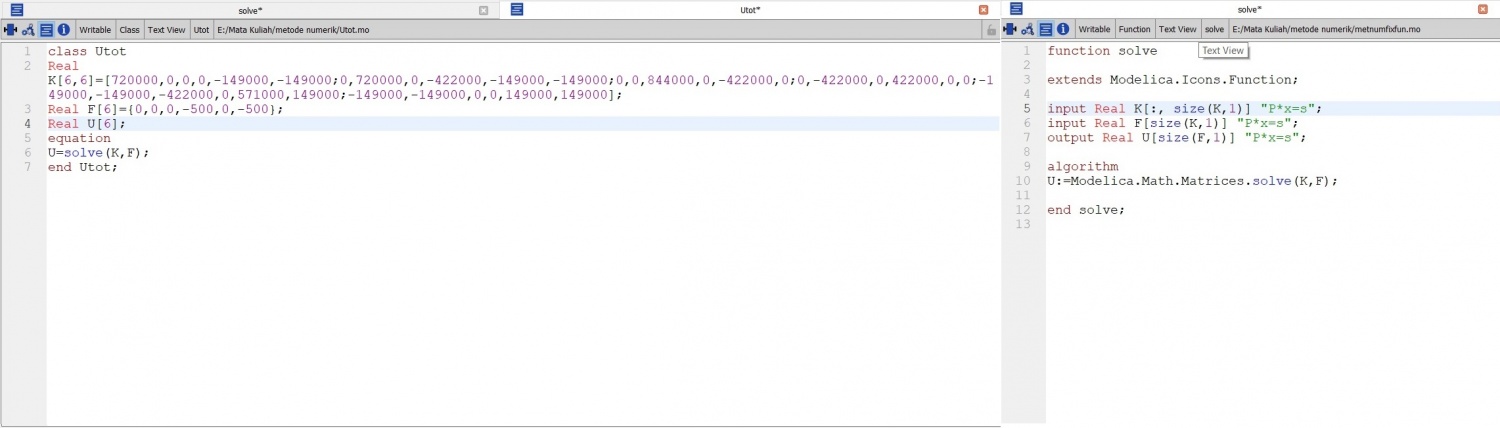
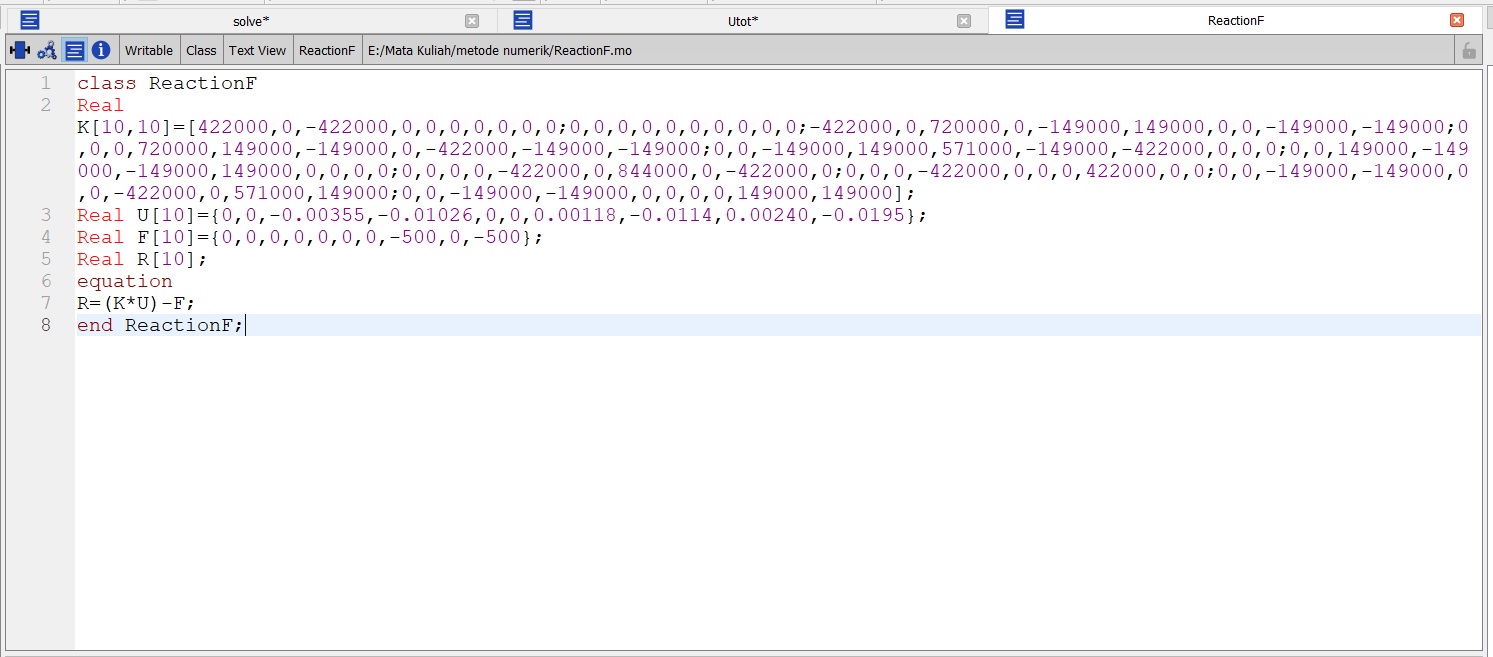
mencari nilai menggunakan fungsi class dan function
sesuai dengan pada pdf
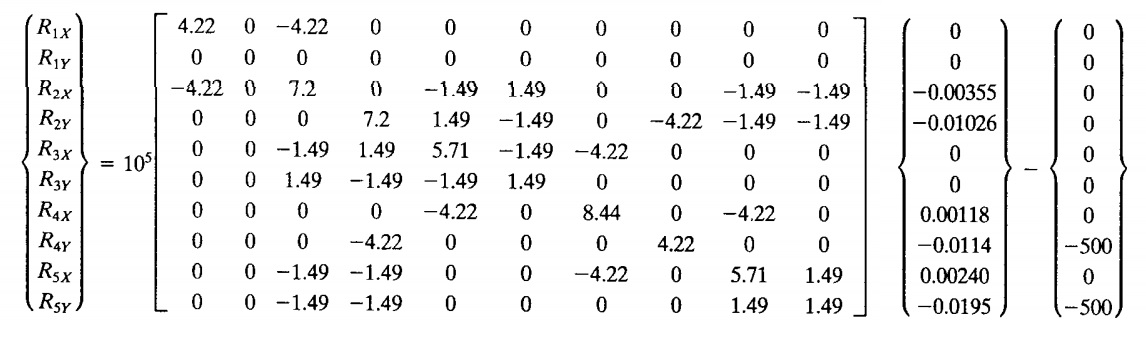
- mencari Reaction Force
R = (K^(G) * U) - F
digunakan fungsi class untuk menyelesaikan matriks tersebut
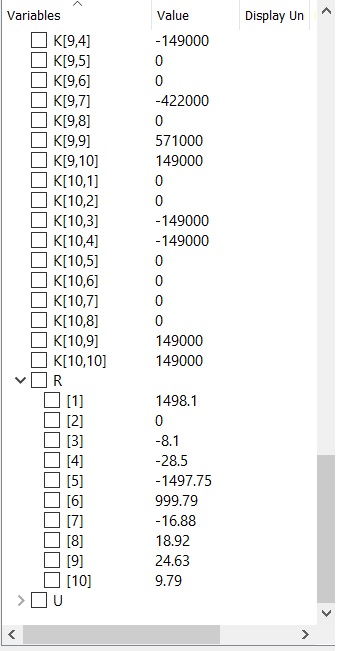
hasil plot
Pertemuan ke-4, 30 November 2020
Analisa Statik, analisis struktural berfokus pada perubahan yang terjadi dalam perilaku struktur fisik yang diamati ketika diberikan dengan gaya atau dalam kasus struktur, beban.
Analisa Dinamik, jika gaya atau beban yang diterapkan memiliki tingkat perubahan kecepatan yang tinggi selama proses maka ia berada di bawah analisis dinamis.
Persoalan
Diberikan permasalahan sebagai berikut :
Step
1. Menentukan elemen dan node pada persoalan, dimana elemen sebagai batang dan node sebagai tumpuan.
2. Menghitung Konstanta Kekakuan pada setiap elemen dengan rumus, K = (A.E)/L.
3. Membuat matriks K-lokal untuk setiap elemen, peletakan nilai-nilai pada matriks mengacu pada node-node yang telah kita tentukan dan memasukan sudut yang telah diketahui.
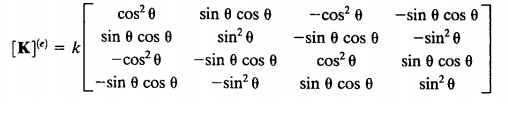
4. Untuk membuat matriks K-Global dibutuhkan penjumlahan dari setip K-lokal, peletakan matriks K-lokal sesuai dari node-node yang telah kita tentukan.
Contoh apabila terdapat 6 elemen dengan 2 tumpuan fix(u=0).
![]()
5.Menghitung defleksi (u) dapat menggunakan F=K.u, dibuat permodelan matriksnya terlebih dahulu.Dan terdapat boundary layer dimana pada setiap elemen yang berhubungan dengan dinding nilai u=0.
6. Menghitung nilai R, dapat menggunakan R = [K]^(G).{u} - F, dimana matriks F dibuat dari data yang diketahui dan peletakannya pada matriks mengacu pada node-node yang telah kita tentukan.
Tugas