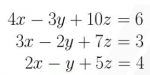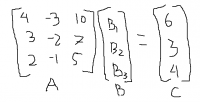Metnum03-Bagus Rangin
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
Assalamualaikum.Wr.Wb. Page di wiki ini menjadi jurnal proses belajar saya pribadi selama belajar di kelas Metoda Numerik 3 setelah UTS. semoga media ini menjadi perantara saya mendapatkan ilmu. aamiin
1.MATERI METODE NUMERIK SEBELUM UTS
Sebelum menjelaskan materi apa saja yang saya pelajari sebelum UTS, alangkah lebih baiknya saya mmenjelaskan penjelasan saya secara garis besar mengenai metode numerik ini. menurut pemahaman saya sejauh ini metode numerik adalah salah satu cara penyelesaian matematika yang memanfaatkan perhitungan berulang dan pendekatan terhadap suatu nilai dalam mencari persamaan,turunan,integral, maupun data. dalam metoda numerik ini seringkali digunakan asumsi terlebih dahulu dan dengan perhitungan yang berulang maka didapatkan nilai yang mendekati eksak. walaupun tidak selalu dalam prakteknya dilakukan perhitungan berulang, namun menurut hemat saya iterasi dalam metode numerik dapat meningkatkan akurasi dari suatu nilai yang dicari.
Sebagai contoh, Interpolasi. Interpolasi adalah proses mencari sebuah data dengan memanfaatkan data sebelum dan sesudahnya. sebenarnya data yang dihasilkan dari proses interpolasi bukanlah data eksak sebenarnya. namun data yang didapatkan dari metoda interpolasi tersebut lah yang paling mendekati dengan melihat pola variabel dan hasil dari data sebelum dan sesudahnya.
Contoh lain dalam Roots of Equation. metode Bracketing Method contohnya. untuk mencari akar dari sebuah persamaan, kita akan diberikan range nilai dari akar tersebut. namun setelah melakukan perhitungan terus menerus maka range tersebut akan semakin kecil sehingga semakin mendekati suatu nilai. hingga akhirnya error atau dx nya semakin kecil hingga error yang diperbolehkan sebelumnya. semakin banyak kita melakukan iterasi maka semakin mendekati sebuah nilai hasilnya.
Sebelum UTS, Kelas Metode Numerik 3 diampu oleh Pak Engkos. dengan bantuan referensi buku Numerical Method For Engineers karya Steven Chapra, kami mempelajari beberapa chapter diantaranya :
1. Part One - Chapter 4 tentang Truncation Error
2. Part TWO (Tentang Roots of Equation) - Bracketing method, Open method, dan Roots of Polynomials
3. Chapter 9 - Gauss Elimination
4. Part five (Curve Fitting) - Least Square dan Interpolation
5. Part Six ( Numerical Differentiation) - Forward, mid, dan backward method
Dari beberapa bagian tersebut akan saya jelaskan lebih lanjut lagi dibawah mengenai apa saja yang telah saya pelajari sampai dengan UTS.
2.Roots of Equation
Pada dasarnya Roots of Equation dalam metode numerik adalah proses mencari akar-akar dari sebuah persamaan. jika dalam metode eksak terkadang sulit untuk mencari akar persamaan, metode numerik ini dapat membantu untuk mencari nilai nya. saat proses belajar kemarin, kami mencoba mencari akar-akar persamaan menggunakan bantuan microsoft excel untuk mencari akar persamaan nya.
Untuk mencari akar sendiri ada dua garis besar yaitu Open Method dan Bracketing method.
Bracketing Method.seperti nama nya, Bracketing method menggunakan kurungan (atau bisa dibilang dua titik yang mengapit nilai) untuk mencari nilai nya. seiring dilakukanya iterasi, maka kurungan tersebut akan semakin kecil dan semakin mendekati nilai sebenarnya. sebagai contoh, suatu akar adalah 5, Bracket akan dibuat pada titik 1 dan 10 dan seiring dilakukanya iterasi berulang maka kurung tersebut akan menjadi 2&9; 3&7; 4&6; 4,5&5,5 dst.. Bracketing method terbagi menjadi 3 yaitu :
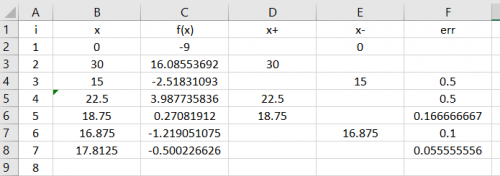
a. Bisection Method : disebut juga metode Bagi-Dua dilakukan dengan terlebih dahulu memilih bagian mana akar berada. dan setelah dilakukan perhitungan dicari bagian mana yang mengandung akar (bagian ini menjadi interval baru). bagian yang tidak mengandung akar dibuang. misal diasumsikan bahwa fungsi f(x) mengandung akar, fungsi kontinyu pada (a,b) dan f(a)f(b)<0 ini berarti f(x) memiliki akar pada interval (a,b). kemudian didefinisikan titik tengah yaitu c= (a+b)/2. lalu dicek pada bagian mana yang mengandung akar, cara mengeceknya adalah dengan mencari apakah f(a).f(c)<0 atau f(b).f(c)< 0. setelah dihitung, maka nilai yang menghasilkan <0 adalah yang mengandung akar (contoh f(a) dan f(c)). sehingga titik a dan c lah yang menjadi interval baru. proses tersebut dilakukan berkali-kali hingga didapatkan error yang sangat kecil atau toleransi yang diinginkan. Pada saat menggunakan teknik ini, kemarin kami menggunakan bantuan microsoft excel.
Berikut adalah salah satu contoh excel dari Bisection Method
b. False Position
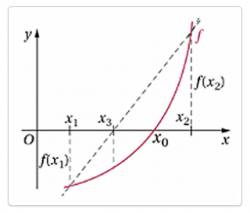
Metode false position atau sering disebut metode titik palsu adalah bentuk modifikasi dari bentuk bagi dua yang dinilai kurang efisien dalam menentukan titik nilai. Metode ini menggunakan pengertian grafis dengan menghubungkan nilai dari kedua titik dengan sebuah garis. Garis tersebut akan memotong di sumbu-x dan akan menjadi taksiran akar yang akan diperbaiki ( semakin mendekati nilai sebenarnya setelah dilakukan perhitungan berulang)
Dengan rumus mencari false position/Xr sebagai berikut:
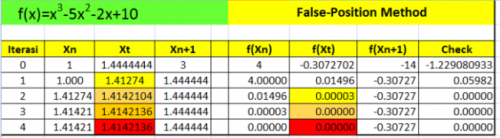
Pada saat kemari, file excel saya untuk formula false position ini hilang namun berikut contoh formula excel yang saya dapatkan diinternet
Open Method berbeda dengan bracketing method, open method hanya memerlukan 1 namun terkadang 2 nilai x perkiraan yang tidak mengurung akar persamaan sebenarnya. saat perhitungan divergen, maka nilai akan menjauhi akar sebenarnya. Namun saat perhitungan konvergen, akar akan ditemukan lebih cepat daripada bracketing method. Open method ini dibagi menjadi 3 metode yaitu : simple fixed point, Newton-Rhapson, dan Secant.
a. Simple Point
b. Newton-Rhapson
c. Secant
Tugas 1, video pembelajaran modelica
Minggu kemarin, Pak Dai memberikan tugas untuk mempelajari modelica dan membuat video tentang pembelajaran nya dan diupload di youtube. berikut hasil video saya dapat dilihat melalui tautan dibawah. Part 1 - https://youtu.be/jqawTQHJBXU Part 2 - https://youtu.be/9pk7_Mm3Yn8
Pertemuan ke-2 Metnum 03(16/11/2020)
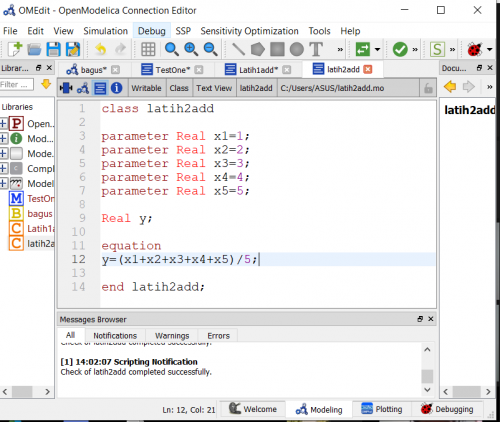
Pada pertemuan kali ini, pertama-tama setiap mahasiswa melaporkan hasil belajarnya mengenai modelica, bagaimana penggunaan dasarnya hingga operasi penggunaan nya.Pak Dai menugaskan di kelas untuk mencoba membuat 2 kelas dengan fungsi class dan class biasa. class function tersebut diisi algoritma untuk y=x+10 yang dimana function tersebut akan dipanggil kembali di class yang satu lagi. pada class yang biasas didefinisikan parameter bahwa x=2 dan y real. pada equation function tadi dipanggil sehingga persamaan equation nya menjadi y= function(x) + 10. sehingga saat di running saya mendapatkan hasil 22. kesalahan dasar saya saat menggunakan modelica adalah lupa nya penggunaan semicolon dan juga lupa mendefinisikan parameter seperti y real.
setelah itu, pak dai menugaskan untuk mencoba membuat model sederhana untuk mencari rata2. gambar-gambar dibawah menunjukan hasil percobaan saya. saya mendefinisikan variabel nya berupa x1, x2, x3, x4, dan x5. dan pada bagian equation terlihat saya menulis y=(x1+x2+x3+x4+x5)/5. dan setelah di running pada gambar bawahnya terlihat hasilnya bahwa y(rata-rata) nya hasilnya 3.
Percobaan sederhana modelica (tugas dari pak dai) untuk membuat program mencari rata rata dari beberapa data. saya menggunakan x1-x5.
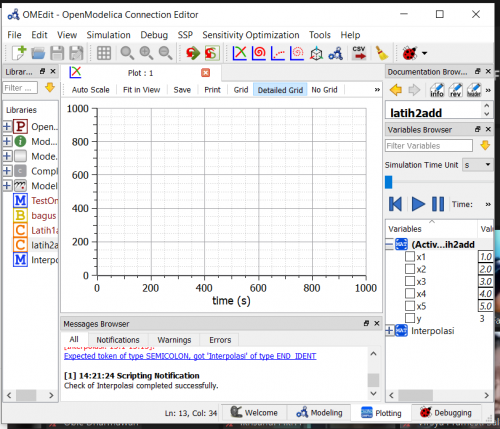
Dan berikut hasilnya setelah dirunning, dapat dilihat rata-rata nya (y) sebesar 3
Lalu untuk selanjutnya pak dai memberikan kita semua tugas untuk membuat model modelica lagi untuk membuat class dengan type function untuk menyelesaikan persamaan-persamaan aljabar simultan ( metoda gauss elimination, gauss seidl, dll...) dan sebuah class function untuk menjalankan fungsi tersebut. tidak lupa juga untuk menggunakan looping dan variable arrays...
Tugas02- Gauss Elimination
Pada pertemuan 2 kemarin, seperti yang telah dijelaskan sebelumnya, pak Dai memberi kami tugas untuk menyelesaikan salah satu persamaan linear simultan dengan open modelica. saya memilih untuk mengerjakan Metode Gauss Elimination sebagai objek percobaan saya didalam penyelesaian modelica. pertama-tama saya mencari soal tentang 3 persamaan linear 3 variable yang nantinya akan diubah menjadi matriks 3x3 dengan persamaan A*B=C. dimana matriks A[3x3], B[3], dan C[3]. soulusi yang dicari adalah pada nilai B1,B2, dan B3.
berikut soal nya...
Setelah itu, persamaan2 tersebut dibuat dalam bentuk matriks sebelum diselesaikan menggunakan gauss, seperti ini...
sesuai dengan perintah pak dai, kita dianjurkan membuat 2 kelas dalam modelica. yang ertama adalah kelas function dimana kita memasukan fungsi algoritma nya. dan kelas yang kedua adalah class dimana nanti function tadi di recall dan dimasukan variable nya lalu solve dilakukan..
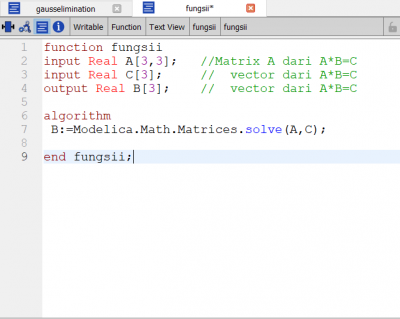
Function Class
function class diisi dengan mendeclare nilai input,outputdan logartima dimana input : A[3,3] dan C[3]
output : B[3]
Logaritma : B:=Modelica.Math.Matrices.solve(A,C)
- logaritma menggunakan fungsi yang sudah ada didalam modelica yaitu fungsi matrices untuk gauss elimination.
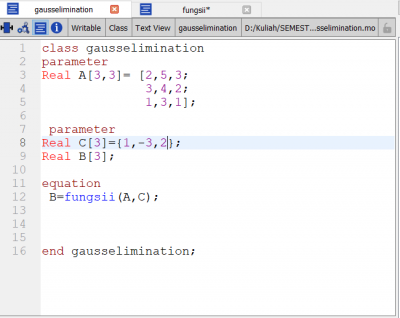
Class gauss elimination
dalam kelas ini, fungsi tadi yang bernama "fungsii" direcall pada kolom equation dengan memasukan A&C sebagai inputnya dan B outputnya. namun sebelum itu terlebih dahulu saya mendeclare nilai2 inputanya tadi seperti digambar atas tersebut.
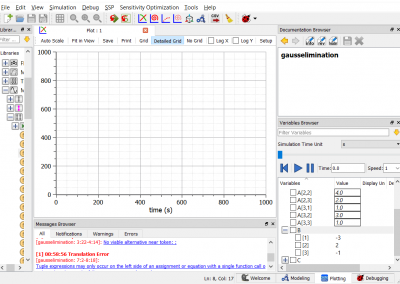
Hasil
setelah itu, kita dapat melakukan plotting dan mendapatkan hasilnya. dari gambar tersebut kita dapat mengetahui nilai dari B adalah = -3, 2, -1.
Note: arahan dari pak dai untuk menggunakan looping dan arrays masih belum dapat saya lakukan karena masih saya pelajari dan belum betuk-betul saya pahami. sumber yang saya pelajari tidak secara langsung mencontohkan aplikasinya pada eliminasi gauss. mungkin kedepanya saya akan dapat melakukan itu.
Pertemuan 3 : 23/11/2020