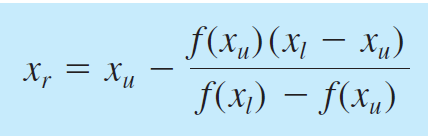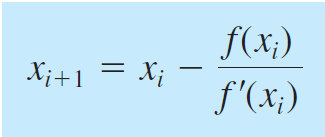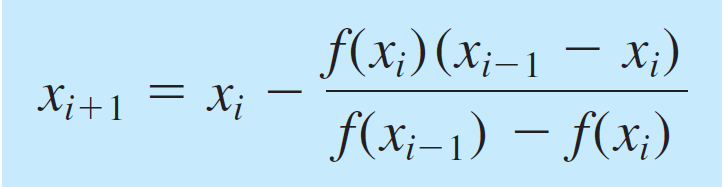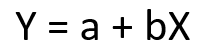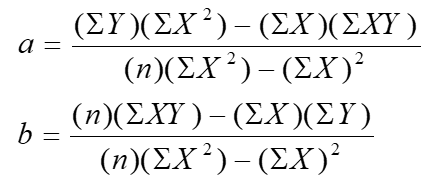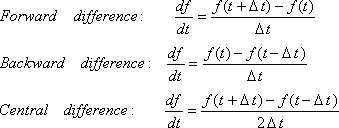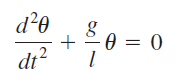Metnum03 Edward Joshua Patrianus Mendrofa

Pertemuan Metode Numerik 03

Pertemuan 1

Metode Numerik adalah salah satu mata kuliah yang sangat banyak penerapannya dalam dunia keteknikan. Mata kuliah ini salah satu mata kuliah yang cukup menarik karena penerapannya sangat luas dan bermanfaat. Sejauh ini yang telah saya pelajari sebelum UTS mencakup 3 materi besar yaitu mencari akar-akar, regresi linier, dan turunan numerik.

1. Mencari Akar-Akar

Pada materi ini, saya mempelajari metode-metode untuk mencari akar secara numerik. Beberapa metode yang saya pelajari adalah metode pencarian akar menggunakan Closed methods (Bracketing Method) dan Open Methods.

Metode Closed Methods merupakan metode pencarian akar-akar dengan menggunakan batas atas dan batas bawah untuk mencari akar dan mengukur persentasi error yang didapat untuk mendapat tingkat akurasi dari iterasi. Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods.

- Graphical Methods

Sebuah metode sederhana yang menggunakan grafik untuk memperkirakan akar-akar suatu fungsi. Metode ini dilakukan dengan melakukan plotting dari suatu fungsi ke dalam bentuk grafik.

- Bisection Methods

Metode ini merupakan salah satu jenis metode incremental search method yang menggunakan batas atas dan batas bawah untuk mempersempit area pencarian akar-akar.

- False-Position Methods

Metode ini sangat mirip dengan metode Bisection. Hal yang membedakan metode False-Position dengan Bisection adalah penentuan titik tengah dari batas-batas yang ditentukan. Penentuan titik tengah dari False-Position Method menggunakan persamaan berikut.

Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method

- Fixed-Point Iteration

Metode ini disebut juga metode iterasi sederhana, adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x)

- Newton-Raphson

Metode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut:

- Secant Method

Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut

2. Regresi Linier

regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.

Persamaan umum Regresi Linier adalah sebagai berikut:

dimana:

3. Turunan Numerik

Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik:

OpenModelica

Untuk mempelajari OpenModelica, saya menggunakan referensi/tutorial dari YouTube dengan tautan berikut:

https://www.youtube.com/watch?v=SW5Eclf1tRs

https://www.youtube.com/watch?v=m0Ahs8fEN28&t=519s&ab_channel=NSTUFACE

Dari video-video tersebut saya diperkenalkan mengenai interface OpenModelica untuk pemula. Saya juga mempelajari bahwa OpenModelica menggunakan bahasa program Modelica untuk penggunaannya. Bahasa ini mirip dengan bahasa pemograman lain seperti python. Kelebihan yang saya lihat dari OpenModelica ini adalah program ini memiliki tools yang membantu mempermudah kita untuk membuat sistem dalam bentuk grafis atau skema. Model-model ini dapat kita aplikasikan dalam kehidupan nyata seperti membuat sistem elektrikal, magnetik, fluida, perpindahan panas, dsb.

Dalam konteks Metode Numerik, saya mempelajari bahwa OpenModelica dapat membantu kita dalam menyelesaikan permasalahan-permasalahan dalam mata kuliah Metode Numerik dan memvisualisasikan penyelesaian tersebut dalam bentuk grafik, salah satunya adalah penyelesaian Persamaan Diferensial Biasa atau ODE.

Contoh penyelesaian permasalahan ODE menggunakan OpenModelica adalah persamaan pendulum, yang didefinisikan sebagai berikut:

Dengan menggunakan referensi dari tautan kedua, saya membuat bahasa pemograman untuk menyelesaikan persamaan pendulum tersebut.

model pendulum

Real y "variable state";

Real x;

parameter Real L=1 "pendulum length";

constant Real g=9.80665;

initial equation

y=9 "initial value";

equation

x=der(y);

der(x)+(g/L)*(y)=0 "differential equation";

annotation(experiment(StartTime = 0, StopTime = 100));

end pendulum;

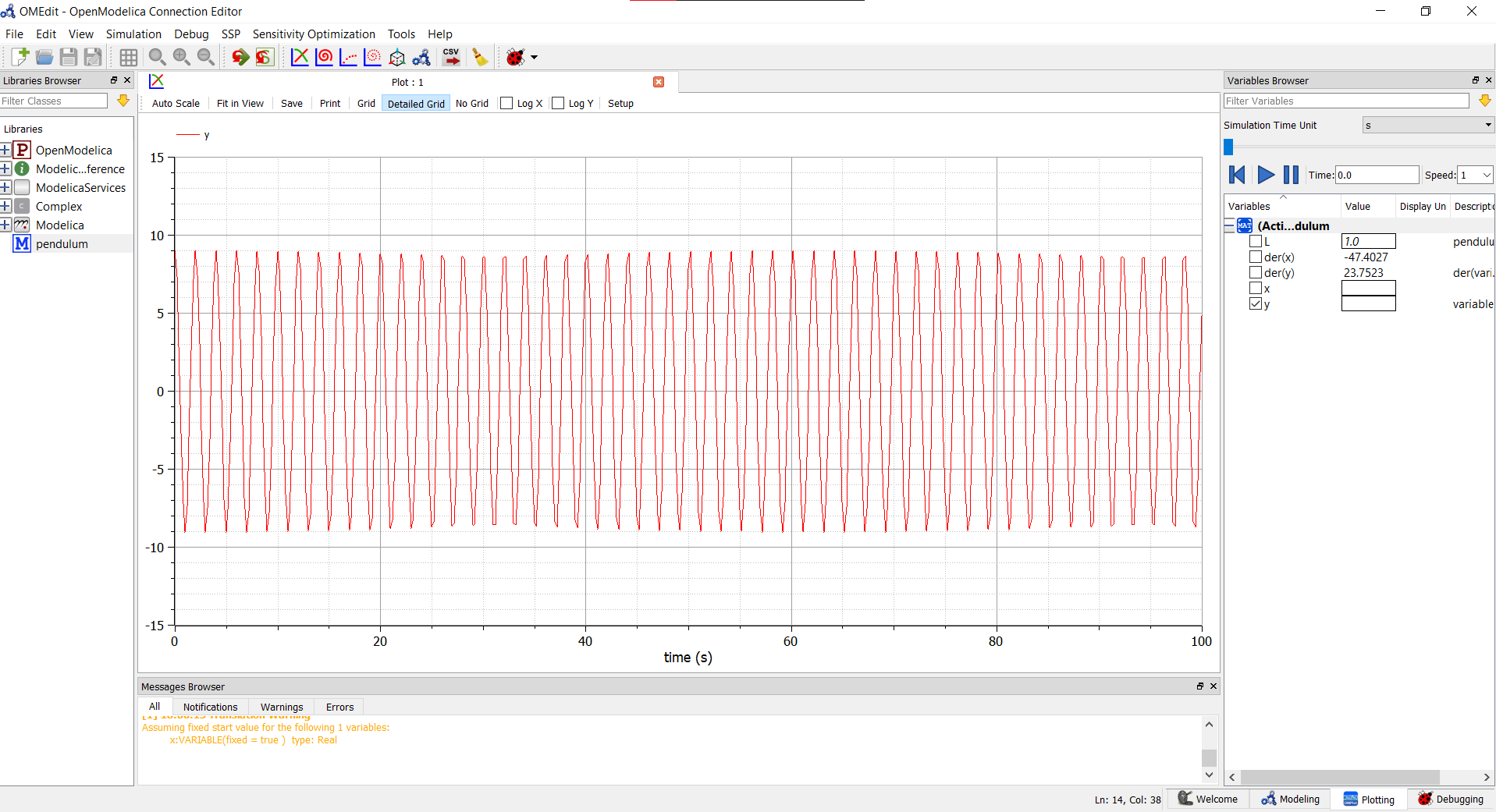
Penyelesaian dari persamaan tersebut digambarkan dalam bentuk grafik sebagai berikut

Dari grafik tersebut dapat dilihat bahwa seiring berjalannya waktu, pendulum melakukan osilasi. Namun dapat dilihat bahwa pendulum tersebut tidak kembali ketitik semula seiring berjalannya waktu.

Dari pembelajaran ini, saya mempelajari bahwa OpenModelica merupakan tools yang berguna dalam pelajaran Metode Numerik.