Turbulent Parallel Plate Flow - CFD Simulation Case study
Contents
Studi kasus dan Terjemahannya
Terjemahan
8.5. AliranTurbulen dalam Pipa (Yunus_A._Çengel,_John_M._Cimbala]_Fluid_Mechanic )
Aliran turbulen dikarateristikan oleh adanya perubahan yang sangat cepat (fluktuasi) dan tak berulang (acak) di dalam region aliran berputar (swirling flow) yang dinamakan eddies (olakan aliran) di seluruh aliran. Perubahan sangat cepat ini memberikan sebuah mekanisme tambahan untuk transfer energi dan momentum. Perputaran olakan aliran dalam aliran turbulen mentransport massa, momentum, dan energi lebih cepat dari difusi molecular dalam aliran laminar, sehingga meningkatkan lebih baik dalam transfer massa, momentum dan panas. Bahkan saat aliran rerata dalam kondisi tunak, gerak olakan mengakibatkan secara signifikan fluktuasi kecepatan temperature, tekanan, bakan densitas (dalam aliran kompresibel). Besarnya nilai sesaat parameter tersebut dinyatakan dengan jumlah komponen rerata (average) dan komponen perubahan (fluktuasi). Sehingga untuk kecepatan sesaat (instantaneous velocity) u = u(bar) + u' sebagaimana ditunjukkan dalam gambar berikut.
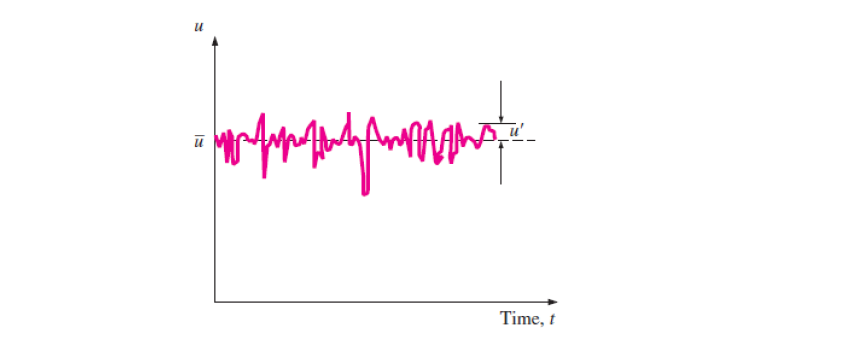Gambar 1. Komponen fluktuasi kecepatan u pada lokasi spesifik dalam medan aliran turbulen.
Nilai rerata sebuah property pada beberapa lokasi ditentukan dengan merata-ratakannya pada suatu selang waktu yang cukup besar sehingga tingkat pererataan waktu konstan. Dengan demikian, pererataan waktu dari komponen fluktuasi kecepatan adalah nol yaitu . Besar beberapa persen dari , frekuensi olakan yang tinggi (orde ribuan per detik) membuatnya sangat efektif dalam perpindahan momentum, energi termal, dan massa. Dalam aliran turbulen stasioner rerata waktu, nilai rerata property tidak bergantung waktu. Fluktuasi tak menentu (chaotic) partikel fluida berperan dominan dalam jatuh tekanan, dan gerakan-gerakan tak berulang ini harus menjadi pertimbangan analisis bersama kecepatan rerata.
Sebagai pemikiran awal yaitu menentukan tegangan geser dengan cara analogi dalam aliran laminar dari , di mana adalah profile kecepatan rerata untuk aliran turbulen. Dan dalam ekperiumental yang menjadi hal pokok adalah tegangan geser yang lebih besar akibat fluktuasi turbulen. Sehingga menjadi hal pemikiran penting bahwa tegangan geser turbulen terbagi menjadi 2 hal yaitu komponen laminar, yang menghitung gesekan antar lapisan-lapisan dalam arah aliran (diekspresikan ) dan komponen turbulen, menghitung gesekan antar fluktuasi partikel fluida dan ‘body’ aliran (ditunjukan dengan τ_turb dan berkaitan dengan komponen fluktuasi dari kecepatan). Kemudian tegangan geser total dalam aliran turbulen dapat diekspresikan sebagai :
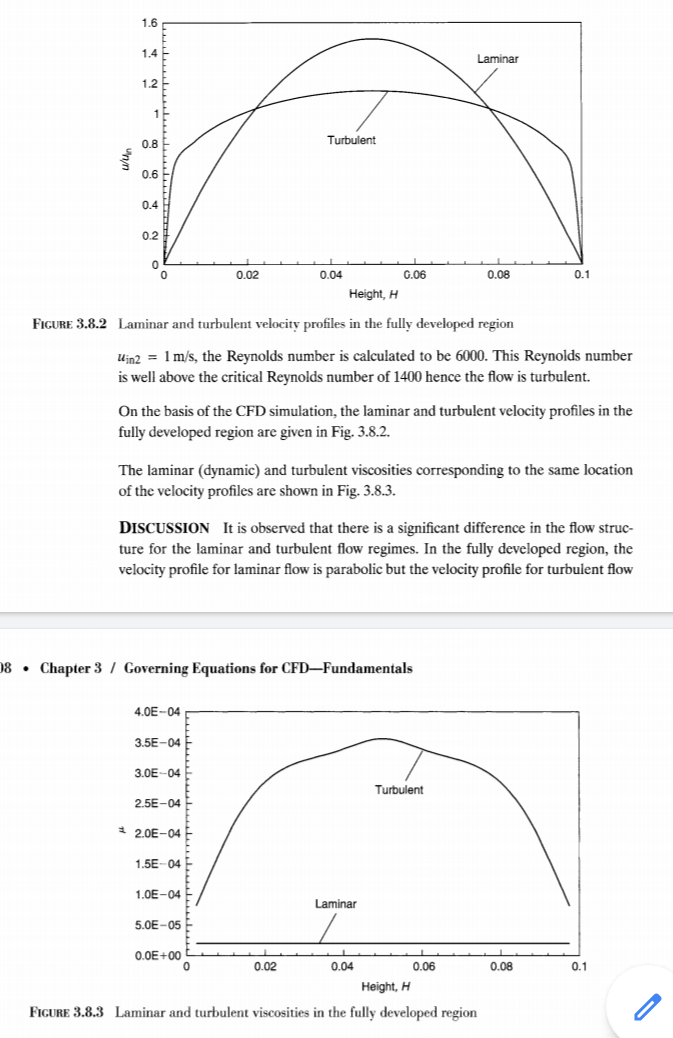
Walaupun profil kecepatan diaproksimasikan parabolik dalam aliran laminar, namun menjadi lebih rata atau lebih penuh dalam aliran turbulen, terutama ketika angka Reynolds meningkat dan kecepatan menjadi hampir seragam sebagaimana aproksimasi profil kecepatan seragam yang umum digunakan untuk aliran pipa berkembang penuh (fully developed). Dan laju aliran pada dinding pipa stasioner selalu nol (non-slip condition).
Gambar 2. Profil kecepatan dan variasi tegangan geser dengan jarak radial
untuk aliran turbulen dalam pipa
Tegangan Geser Turbulen
Sebuah aliran turbulen dalam suatu pipa mendatar, gerak olakan ke atas partikel fluida dalam sebuah lapisan kecepatan lebih rendah ke lapisan berdampingan berkecepatan lebih tinggi melalui sebuah luasan diferensial sebagai hasil fluktuasi kecepatan . Kenaikan laju massa aliran melalui luasan dA tersebut sebesar ρv'dA memberikan akibat pada penurunan kecepatan rerata aliran pada lapisan di atasnya, karena adanya perpindahan momentum dari partikel fluida dengan kecepatan rerata yang lebih rendah. Kemudian transfer momentum ini juga menyebabkan kecepatan mendatar partikel fluida meningkat oleh dengan pertambahan momentum pada laju (ρv^' dA)u', yang sama dengan penurunan momentum lapisan fluida lebih atas. Gaya yang bekerja pada arah perindahan partikel fluida di atas luasan dA adalah δF=(ρv^' dA).(-u^' )= =-(ρv^' dA) u^'. Dan besarnya tegangan geser sesaat (instantaneous shear stress) pada luasan area dA akibat gerak olakan yaitu δF/dA==-ρu'v'. Kemudian besarnya tegangan geser turbulen dapat diekspresikan menjadi
τ_turb=-ρ(u'v') ̅ (2)
Rerata waktu perkalian dot (u'v') ̅≠0, meskipun (u^' ) ̅=0 dan (v^' ) ̅=0, hasil eksperimental menunjukkan bahwa (u'v') ̅ biasanya sebuah kuantitas negatif. Suku -ρ(u'v') ̅ atau 〖-ρ(u') ̅〗^2 dinamakan tegangan Reynolds atau tegangan turbulen. Gerak olakan tak berulang dari kelompok partikel menyerupai gerak tak berulang molekul-molekul gas nertumbukan satu sama lain sesuah berpindah pada suatu jarak dan bertukaran momentum dalam proses. Dapat dikatakan bahwa transport momentum oleh olakan-olakan analog dengan ifusi momentum molecular. Dalam model turbulen yang lebih sederhana, analogi oleh Joseph Boussinisque diekspresikan dengan
τ_turb=-ρ(u^' v^' ) ̅= μ_t (∂u ̅)/∂y (3)
Dengan μ_t adalah viskositas olakan (eddy viscosity) atau viskositas turbulen (turbulent viscosity) yang menghitung transport momentum oleh olakan-olakan turbulen. Tegangan geser total dinyatakan oleh
τ_total=(〖μ+μ〗_t ) (∂u ̅)/∂y= ρ(〖ϑ+ϑ〗_t)(∂u ̅)/∂y (4)
Di mana ϑ_t=μ_t/ρ merupakan viskositas olakan turbulen atau viskositas turbulen kinematic (juga dinamakan difusivitas olakan momentum).
Viskositas olakan dimodelkkan sebagai suatu fungsi variabel-variabel aliran rerata yang disebut dengan ‘closure’ viskositas olakan. Prandtl memperkenal konsep ‘mixing length’ yang berkaitan dengan ukuran rerata olakan-olakan yang terlibat dalam pencampuran, dengan ekspresi tegangan geser berikut :
〖τ_total=μ_t (∂u ̅)/∂y= ρ〖l_m〗^2 ((∂u ̅)/∂y)〗^2 (5)
Namun konsep ini terbatas penggunaan karena lm adalah tidak konstan (area sekitar dinding, lm proporsional terhadap jarak dari dinding) dan merupakan fungsi dari variabel aliran rerata, jarak dari dinding, dan sebagainya.
