Tugas 2 pondasi by rohmat
Pemodelan dan Analisis Stuktur Pondasi Rumah Panggung dengan EES Definisi Masalah
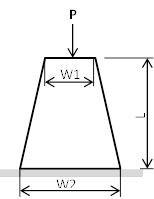
Terdapat sebuah pondasi rumah pangung diberikan beban P (seperti gambar di samping). Dimana ukuran panjang penampang atas disebut W1 dan penampang bawah W2, tinggi dari pondasi adalah L, dan ketebalan pondasi disebut T. Sedangkan berat pondasi diabaikan, cobalah analisa dengan metode numerik menggunakan aplikasi EES.
Tinjauan Teori [1]
1. Tegangan tarik
Tegangan tarik adalah besar gaya tarik dibagi dengan luas penampang suatu benda. Tegangan tarik termasuk gaya persatuan luas.
Rumus :
σt = F/A
σt = Tegangan tarik (kg/cm²)
F = Gaya yang bekerja/beban (kg)
A = Luas penampang (cm²)
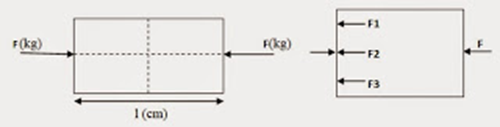
2. Tegangan tekan
Tegangan tekan adalah tegangan yang terjadi di dalam suatu batang apabila gaya-gaya luar yang bekerja padanya adalah gaya-gaya tekan.
Bila F adalah gaya luar yang bekerja dan A adalah penampang lintang dari batang, maka rumus tegangan tekan dapat ditulis :
σd = F/A
σd = Tegangan tekan (kg/cm²)
F = Gaya yang bekerja/beban (kg)
A = Luas penampang (cm²)
3. Pengaruh Pembebanan Terhadap Bahan
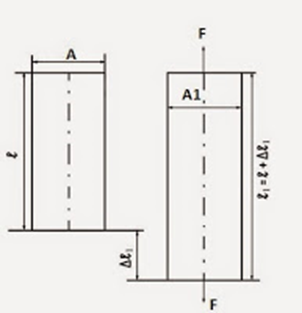
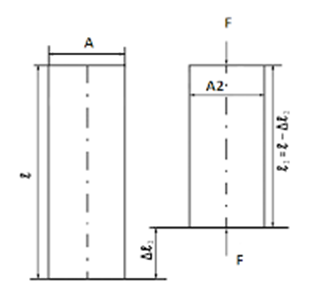
Pada suatu bahan yang menerima beban tarik akan timbul gaya tarik dan adanya tegangan tarik ini akan mengakibatkan bahan bertambah panjang. Demikian juga pada pembebanan tekan, pada bahan yang bersangkutan akan terjadi perpendekan. Selain itu juga terjadi perubahan pada penampang lintangnya, pada beban tarik penampang akan menjadi lebih kecil dan pada beban tekan penampang akan menjadi lebih besar.
Hukum eksperimental Hook menyatakan “Dalam batas-batas tertentu, perpanjangan atau pemendekan suatu bahan adalah berbanding langsung dengan bebannya terhadap panjang mula-mula, namun berbanding terbalik terhadap penampang bahannya.”
Gambar tegangan tarik dan tekan
Pertambahan panjang atau perpendekan juga dipengaruhi oleh sifat-sifat dari bahan, sehingga rumusnya adalah :
∆l = C x F x l/A
∆l = pertambahan panjang atau perpendekan (cm)
C = koefisien perpanjangan
F = besar pembebanan (kg)
l = panjang bahan sebelum dibebani (cm)
A= penampang bahan (〖cm〗^2)
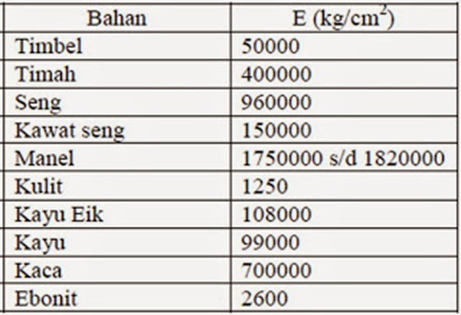
Namun harga C untuk bahan-bahan logam sangat kecil, maka untuk mempermudah perhitungan dipakai harga kebalikannya yang disebut modulus kenyal (E = 1/C). Sehingga rumusnya menjadi :
∆l = (F x l) / (E x A)
∆l/l adalah perubahan panjang untuk setiap satuan panjang bahan yang disebut perpanjangan spesifik disingkat ε. Dan F/A adalah tegangan pada bahan, sehingga rumusnya menjadi :
ε=( F×l)/(A×ΔL)
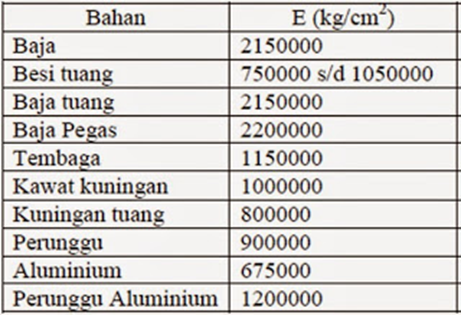
Tabel Modulus Kenyal Beberapa Bahan:
4. Displacement (Lendutan)
Lendutan adalah peralihan dalam arah y dari sembarang titik di sumbu balok. Bila sebuah balok dibebani maka sumbu longitudinal yang semula lurus akan berubah menjadi kurva yang disebut kurva lendutan dari balok. Dalam perencanaan bangunan, dimana biasanya ada batas maksimum untuk lendutan, karena lendutan yang besar akan mengakibatkan penampilan yang jelek dan struktur yang terlalu lemas.
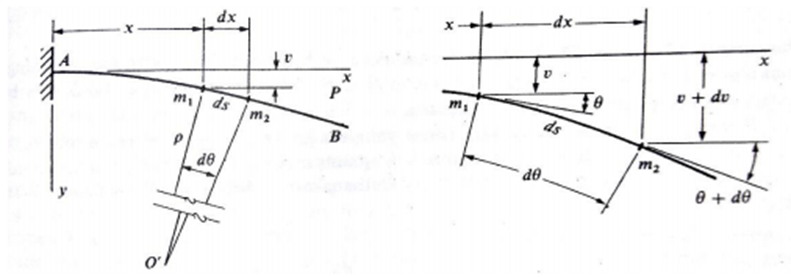
Kurva lendutan pada balok
Lendutan balok υ dari titik m1 yang berjarak x dari pusat adalah translasi (pergeseran) titik tersebut pada arah y, yang diukur dari sumbu x ke kurva lendutan. Lendutan ke atas maka berniali positif dan jika ke bawah maka bernilai negatif. Balok yang dirancang dengan baik tidak hanya mampu memikul beban yang akan diterimanya tetapi juga harus mampu mengatasi terjadinya defleksi sampai batas tertentu.
Persamaan diferensial dasar untuk kuva lendutan suatu balok:
(d^2 y)/〖dx〗^2 =M/EI
Keterangan:
y = defleksi balok
M = momen tekuk pada jarak x dari salah satu ujung balok
E = modulus elastisitas balok
I = momen inersia penampang melintang terhadap sumbu netral
5. Penyelesaian Menggunakan EES
Dengan tinjauan teori yang sudah ada di atas, maka langkah selanjutnya adalah mengasumsikan parameter-parameter yang dibutuhkan. Parameter-parameter tersebut adalah sebagai berikut: (bahan baja)
P = 1000 kg
W1 = 500 mm
W2 = 1000 mm
L = 1000 mm
t = 500 mm
E = 215x104 Kg/cm2
Dari beberapa parameter yang sudah disebutkan di atas, langkah selanjutnya adalah meninjau tegangan, regangan dan displacement dari 5 titik. Berikut algoritma yang sudah dimasukkan ke EES:
Maka setelah kita solve, hasil komputasinya adalah sebagai berikut: