Alwi faris
السلام عليكم
بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم
Nama saya Alwi Faris Syahab,NPM:1806202550, biasa di panggil ais, saya lahir di jakarta, tanggal 14 agustus 2000. saya berasal dari jakarta, tetapi saya keturunan arab.
Pengetahuan saya tentang pemograman saya pernah memiliki blogspot, tetapi sudah lama sehingga membuat saya lumayan terlatih tentang bahasa-bahasa komputer saya juga dapat menggunakan excel dengan cukup baik dan saya mahir dalam menggunakan komputer
Contents
- 1 Biodata
- 2 TUGAS 1 METODE NUMERIK
- 3 Pertemuan Ke-2 (Jumat, 14 Februari 2020)
- 4 Tugas 2 Alwi Faris
- 5 Progres Belajar Metode Numerik - Alwi Faris
- 6 Pertemuan ke 3 (Metode Runge Kutta)
- 7 Laporan Asistensi (25 FEBRUARI 2020)
- 8 Laporan Asistensi (3 Maret 2020)
- 9 IVP dan BVP
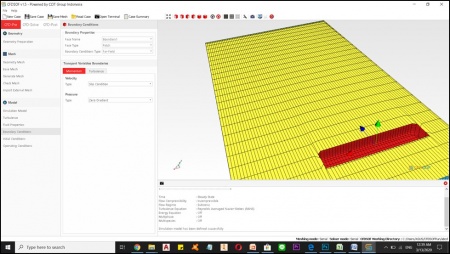
- 10 Pertemuan Ke- 6(Tugas Optimasi)
Biodata
Nama: Alwi Faris
Tempat Lahir: Jakarta
Usia: 19 tahun
Alamat: Jl. Siaga 2C No. 37, Pejaten Barat, Jakarta Selatan
Jenis kelamin: Laki-laki
Agama: Islam
Kewarganegaraan: Indonesia
email: Faris.syahab@gmail.com
TUGAS 1 METODE NUMERIK
pada tugas 1 Metode Numerik ini mahasiswa di minta untuk menyelsaikan persamaan f(x) = (x^2-1)/(x-1) dan x = 1dengan cara manual dan menggunakan aplikasi
Link Tugas Tugas 1 Alwi Faris Tugas 2 Alwi Faris
Perhitungan Manual
Ketika x di masukan kedalam fungsi maka di dapat hasil 0/0 sehingga untuk menyelesaikan persamaan tersebut digunakan metode limit agar mendapatkan peyelesaian dari fungsi tersebut.
Perhitungan Menggunakan Aplikasi(Phyton 3.8)
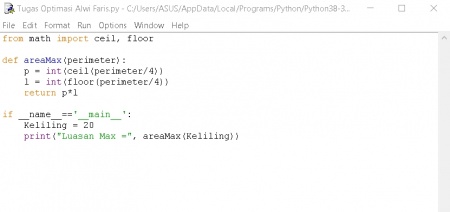
hal yang harus pertama di lakukan adalah membuat algoritma,
dapat di lihat seperti gambar di bawah ini algoritma untuk menyelesaikan persamaan
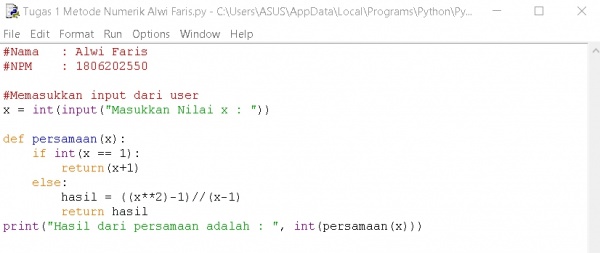
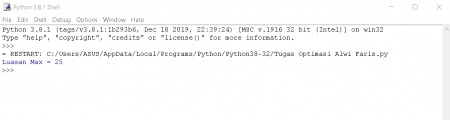
setelah itu, save dan langsung bisa di berikan input dan persamaan langsung dapat terselesaikan
seperti gambar berikut
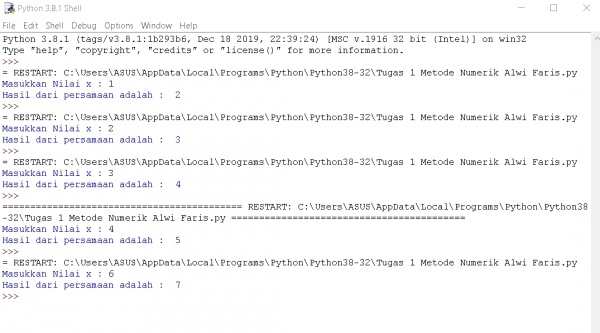
Komentar
Dengan menggunakan aplikasi persamaan dapat terselesaikan dengan sangat mudah dan sangat cepat, tetapi untuk persamaan di ini perhitungan manual menurut saya lebih mudah karena persamaan tidak terlalu kompleks dan sulit, penggunaan aplikasi sangat berguna ketika kita menemukan persamaan-persamaan yang sulit dan memakan waktu ketika kita menyelesaikannya dengan cara manual
Pertemuan Ke-2 (Jumat, 14 Februari 2020)
pertemuan kali ini pak DAI memberikan kesempatan untuk melihat soal sola yang ada di E-book yang di berikan (Numerical Methods in Engineering with Phyton3)
berikut adalah soal-soal yang menarik perhatian saya
Soal di bawah ini berada pada BAB 9 (Symmetric Matrix Eigenvalue Problems)
Referensi: Kiusalaas, Jaan. 2013. Numerical Methods in Engineering with PYTHON 3. NEW YORK:Cambridge University (Press halaman : 346-347)
Saya tertarik dengan soal ini karena menyelesaikan matrix eigen dengan cara lain dan saya ingin mengetahuinya karena menurut saya ketika saya belajar pada mata kuliah Aljabar Linier dan mencari nilai eigen dengan cara manual cukup memakan waktu
Tugas 2 Alwi Faris
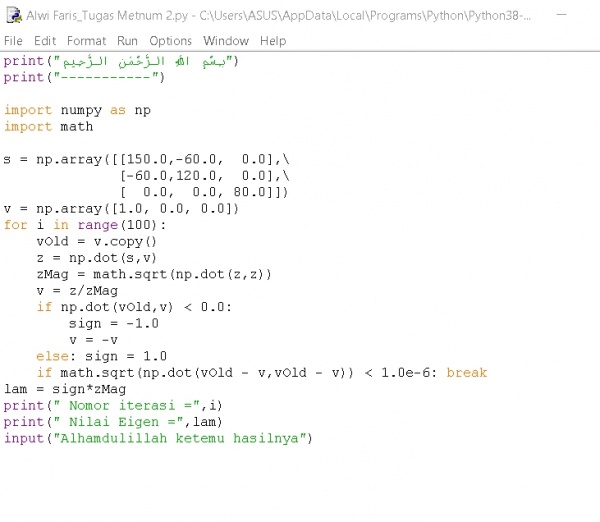
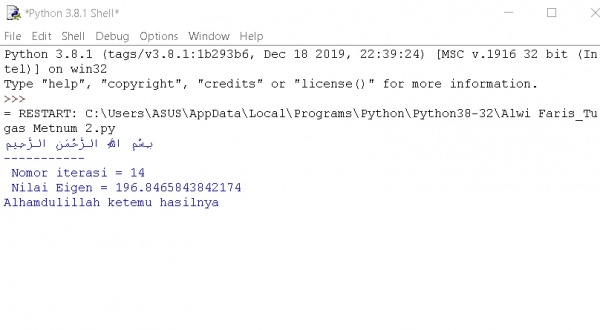
Menyelesaikan Soal pada BAB 9 (Symmetric Matrix Eigenvalue Problems) saya mengerjakan soal no 4 dengan menggunakan phyton mendapatkan nilai eigen sangat cepat
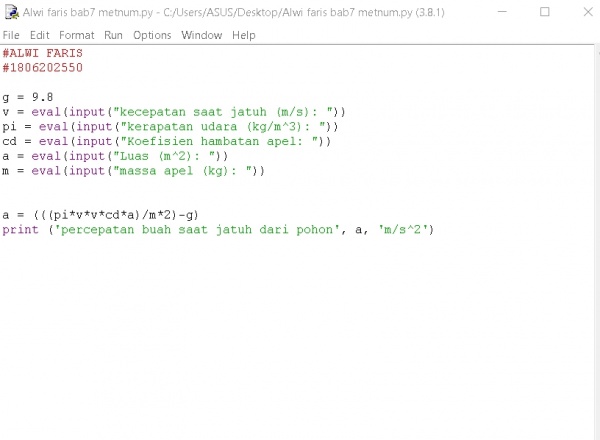
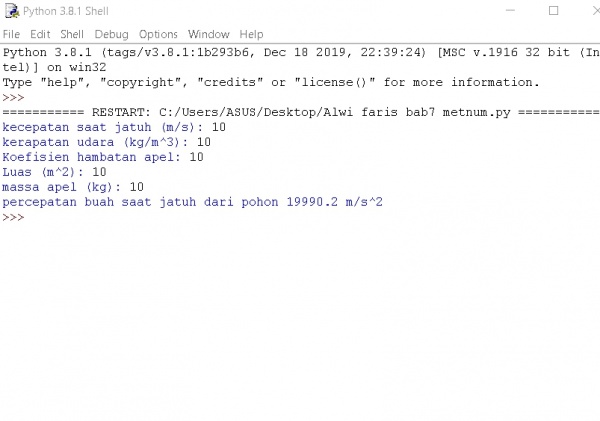
Buah Jatuh dari Pohon
dengan menggunakan phyton dibuat sistem sehingga kita tinggal menginput data-data dan langsung mendapatkan hasilnya
Progres Belajar Metode Numerik - Alwi Faris
LinkProgres Belajar Metode Numerik - Alwi Faris
Alhamdulillah Setelah 2 minggu belajar metode numerik saya mendapatkan ilmu-ilmu baru dan saya akan mengambil hikmah dari ilmu yang bermanfaat
Pertemuan ke 3 (Metode Runge Kutta)
# x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment dengan nilai h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Masukkan Nilai t(+)")
Laporan Asistensi (25 FEBRUARI 2020)
Laporan Asistensi (3 Maret 2020)
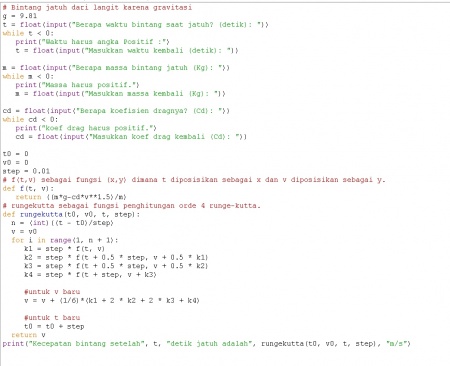
IVP dan BVP
Ivp(menghitung kecepatan bintang jatuh
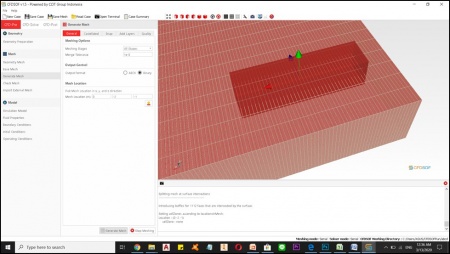
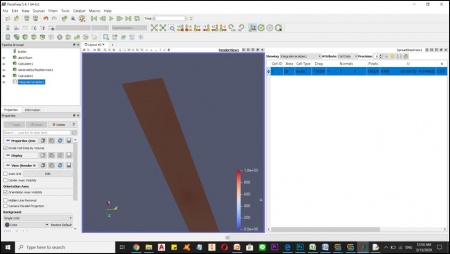
Bvp (menghitunh disttibusi berat pada balok)