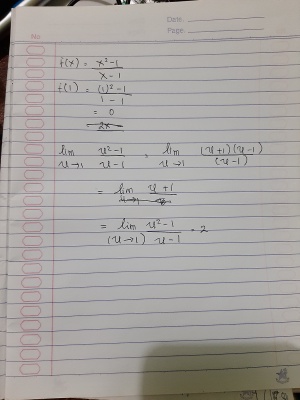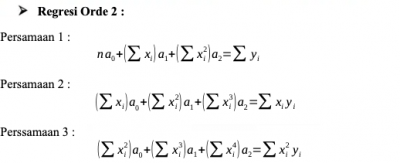Vita Puspita
Contents
Vita Puspita
Lahir di Jakarta, 13 Mei 2000, menyukai menonton film dan tidur. Berkuliah FTUI
Mengenal Programming
Saya belajar programming, dari seorang mahasiswa fasilkom UI menegnai pembuatan website. Di Bidang Perkapalan, penggunaan Programming berlaku dari perancangan hingga mencari kegagalan dalam material beserta optimasi penggunaan energi di kapal.
Tugas 1
Cara Manual
Menggunakan perhitungan manual, dengan menyelesaikan masalah dengan penggunaan limit. Hasil yang didapatkan saat diawal adalah 0, yang dimana tidak terdefinisi. Ketika dengan penggunaan limit, mendapatkan hasil f(x)=2
Cara Phython
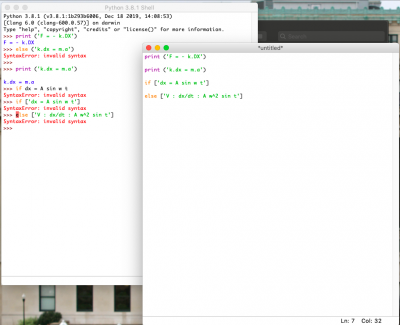
Saya baru mencoba phython pertama kali, dengan menggunakan perhitunga komputasi. Perhitungan yang biasa dilakukan jauh lebih singkat dan cepat. Tahapan 1: membuat file baru, kemudian mulai mencoba membuat command Tahapan 2: membuka phython shell, agar command yang sudah kita rancag dari awal akan terkomputasi secara otomatis dengan hasil yang sesuai
Tugas 2.1
Apa saja yang dipelajari di Metode Numerik?
Banyak hal yang sudah dipelajari di Metode Numerik. Metode Numerik merupakan sebuah mata kuliah yang mengenalkan dasar programming until bidding keteknikan.
Tugas 3
Konservasi Momentum Pegas
Hari Selasa kemarin saya mempelajari tentang Konservasi momentum pegas dengan cara python
Runge-kutta sebagai alternatif perhitungan
Pemodelan Pegas dengan Menggunakan Metode Runga Kutta
X0 dan y merupakan increment dengan nilai h = 0,01
X0= 0 Y= 0 H= 0,01 X= float (input(“Masukan nilai t:”)) if 0<= X <2:
- dydx menyatakan persamaan awal dalam soal. Persamaan diintegralkan untuk mendapatkan kecepatan.
- Didapatkan hasil 2x^2-30*x*y , karena menggunakan massa = 2,5 kg dan konstatnta pegas k = 75N/m
- P(t) dinyatakan dalam x.
Def dydx(x,y):
- P(t) dinyatakan dalam x,def dydx (x,y):
Return (2*x**2-30*x*y)
Merupakan implementasi perhitungan Range-kutta , def Rungekutta(x0, y0, x, h):
n = (int) ((x-x0)/(h) y = y0
k1 = h*dydx(x0,y) k2 = h * dydx (x0 + 0,5 * h,y +0,5*1) k3 = h* dydx (x0 + 0,5 *h, y + 0,5*k2) k4 = h* dydx (x0+h, y +k3)
y= y+(1,0/6,0)*(k1 + 2 * k2 +2 *k3)
Mengikuti persamaan dengan memasukan nilai positif.
Laporan 2
Tugas 4
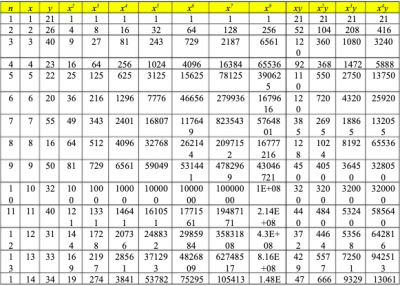
Regresi Linear dengan menggunakan metode manual yang dimana terdapat beberapa data,dengan menggunakan orde yang cocok (orde 2, orde3, orde 4)
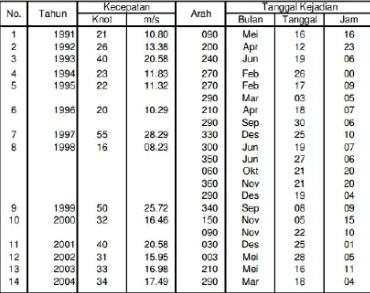
Pada data tersebut nanti akan diproses dengan perhitungan kalkulus
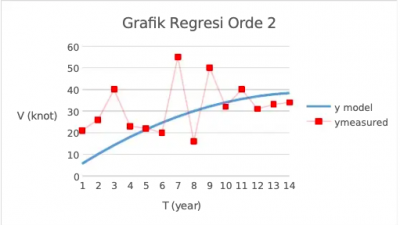
Dengan meneumakan y dan nilai error yang dibutuhkan, kemudian plot data untuk diubah ke dalam grafik
Tugas 5
Boundary Value Problem dan Initial Value
Boundary Value Problem merupakan sistem persamaan diferensial dengan penyelesaian dan nilai penurunan yang spesifik lebih dari satu fokus, Biasanya, penyelesaian dan penurunan ditunjukan hanya untuk dua titik (the boundaries) yang menjelaskan sebuah two-point value problems (Ian Gladwell, scholarpedia.org)
Initial Problem ditunjukan untuk penyelesaian pada initial condition y(t0)=A, Penyelesaian mengharapkan bahwa F(t,y) akan terus lanjut pada bagian yang melibatkan A dan turunan sebagian ∂Fi/∂yj yang terikat, dengan asumsi dimana initial value problem memilki penyelesaian
Boundary Value Problem menujukan penyelesaian, dengan memperlihatkan kondisi lebih dari satu titik, Blasius Problem merupakan persamaan diferensial y‴=−yy″/2 dengan adanya boundary condition y(0)=0,y′(0)=0,y′(∞)=1
Kasus
1. (Boundary Value Problem) Software test, dengan menggunakan boundary value problem yang dimana menggunakan nilai maksimun dan nilai minimun untuk mendapatkan nilai valid. 2. (Initial Value) Untuk menghitung panjang lintasan bisbol yang dilempar dari bidang tengah lapangan bisbol ke outfielder dengan kecepatan dan sudut horizontal yang ditentukan