Kanwaljot Kaur
Nama: Kanwaljot Kaur
NPM : 1706036305
Mahasiswa Teknik Mesin 2017
Contents
[hide]- 1 Pertemuan Pertama
- 2 Pertemuan Kedua
- 3 Pertemuan Ketiga
- 4 Pertemuan Keempat
- 5 Pertemuan Kelima
- 6 Pertemuan Keenam
- 7 KUIS
- 8 UTS
- 9 PERBAIKAN UTS
- 10 Pertemuan kesembilan: Pemodelan Runge Kutta
- 11 Tugas: CFD (mobil)
- 12 TUGAS ANALISIS GAYA LIFT FORCE DAN DRAG FORCE PADA AIRFOIL (CFDSOF-NG)
- 13 Penjelasan tentang ANN
Pertemuan Pertama
Hari, Tanggal : Rabu, 4 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan pertama mata kuliah metode numerik, Pak Dr. Ahmad Indra, atau yang biasa disapa Pak Dai, memberikan pendahuluan yang intinya adalah setiap mata kuliah yang kita ambil jangan hanya asal lewat saja, tetapi kita harus menyerap 'ilmu-ilumnya'. Untuk contohnya, Pak Dai memberikan sebuah pertanyaan, yaitu 'Kenapa sebagai mahasiswa teknik mesin kita harus mempelajari kalkulus?' Kemudian setelah beberapa teman mencoba menjawab, akhirnya beliau memberikan alasan mengapa kita harus mempelajari kalkulus, yaitu kita dapat mengambil ilmunya seperti menurunkan rumus dan juga logika matematika yang nantinya dapat digunakan di mata kuliah mesin seperti matematika teknik, termodinamika, dan mata kuliah lainnya.
Metode Numerik adalah teknik yang digunakan untuk menyelesaikan persoalan matematika sehingga dapat diselesaikan dengan operasi perhitungan biasa, yaitu tambah, kurang, kali, dan bagi.
Pada metode numerik ini, bahasa pemograman yang digunakan adalah Python. Meskipun metode numerik digunakan sebagai penyelesai masalah atau solver, ide untuk menyelesaikan persoalannya tetap berasal dari manusia. Untuk menyelesaikan persoalan matematika itu dibutuhkan langkah-langkah yang merupakan instruksi yang dibutuhkan komputer. Maka, dibutuhkan bahasa penulisan dari yang kita (manusia) mengerti menjadi bahasa mesin yang disebut bahasa pemograman. Untuk mempermudah kita dalam membuat bahasa pemograman ini, digunakan flow chart, yang merupakan instruksi yang terdiri dari bagan dan simbol tertentu.
Pak Dr. Eng. Radon Dhelika, atau yang kerap disapa Pak Radon, menambahkan bahwa di industri 4.0 ini tingkat kebutuhan skill pemograman dibutuhkan. Maka kita harus fokus, menyerap, dan mendalami mata kuliah metode numerik ini.
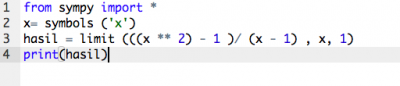
Diakhir pertemuan pertama berakhir, diberikan tugas sebagai berikut: 1. Mempelajari Python masing-masing 2. Membuat penyelesaian untuk persoalan T(x)= (x^2-1)/(x-1) dalam bentuk algoritma / flowchart
Setelah saya membaca dan menyari dari berbagai sumber, saya menetukan algoritma dari persoalan yang diberikan dengan menggunakan sympy
from sympy import *
x = symbols ('x')
hasil = limit (((x ** 2) - 1 ) / (x - 1) , x, 1)
print (hasil)
Hasil yang didapatkan adalah 2
Pertemuan Kedua
Hari, Tanggal : Rabu, 11 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan kedua kelas metode numerik ini membicarakan banyak hal, salah satunya adalah Artificial Intelligence (AI). AI atau rekayasa kecerdasan ini berguna untuk membantu manusia dan memang dibuat menyerupai manusia. Namun, perbedaan dari manusai dengan robot yang menyerupai manusia adalah manusia memiliki hati, meskipun manusia memiliki keterbatasan yang tidak dimiliki robot.
Dengan mempelajari mata kuliah metode numerik ini, membuat kita berhubungan dengan komputer. Istilahnya komputer adalah 'partner' kita. Maka dari itu, kita harus mengenal 'partner' kita ini, mulai dari istilah-istilah yang ada. Salah satu istilah yang paling sering didengar adalah 32 bit dan 64 bit.
Perbedaan 32 bit dan 64 bit adalah sistem operasi 32 bit hanya dapat menggunakan RAM dengan kapasitas maksimal 4 GB, selain itu sistem operas 32 bit hanya mampu memproses data sebesar 64 nilai komputasi. Sedangkan sistem operasi 64 bit dapat membaca RAM dengan batas maksimal 192 GB dan dapat memproses data hingga 256 nilai komputasi dalam sekali pemrosesan. Seperti hal nya otak manusia yang dapat menyimpan data dalam binary digit, maka komputer dengan sistem operasi 64 bit memiliki kemampuan yang lebih akurat dan juga cepat.
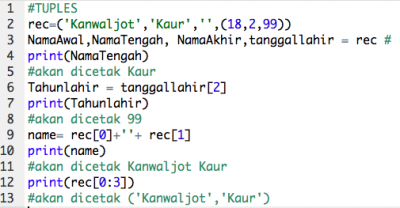
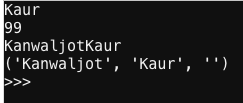
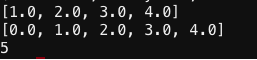
Pada pertemuan kali ini, kita diminta untuk berlatih dalam penggunaan tuples dan juga lists di Python. Berikut hasil latihan saya:
tuples:
lists:
Pertemuan Ketiga
Hari, Tanggal : Rabu, 18 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
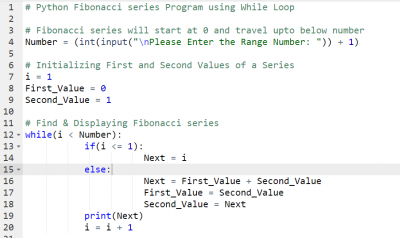
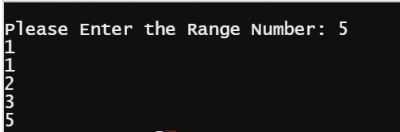
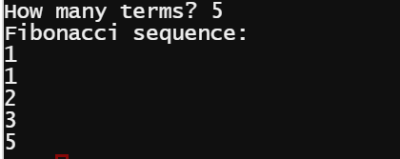
Pada pertemuan ketiga mata kuliah metode numerik, tanggal 18 September 2019, diadakan kuis mengenai bahasa dasar pada python. Kuis yang diberikan aadalah deret Fibonaci. Berikut cara mendapatkan deret Fibonaci sesuai dengan n yang kita inginkan (n adalah suku ke-n pada deret Fibonaci):
Metode Loop While Condition
Metode Function
Pertemuan Keempat
Hari, Tanggal : Rabu, 25 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Topik pembahasan pada pertemuan keempat metode numerik ini adalah pemodelan komputer. Pak DAI mengatakan untuk mengerti sebuah konsep lebih baik, ada baiknya kita memahami apa isi konsep tersebut terlebih dahulu. Numerical computing atau pemodelan komputer ini terdiri dari modelling dan computation.
Kita harus menghitung karena kita ingin dan harus memastikan hal yang kita design harus berfungsi dengan baik dan reliable dengan fungsi yang optimal. Namun manusia memiliki keterbatasan, maka kita menghitung menggunakan pendekatan.
Apa itu model?
Model adalah sebuah representasi yang mensimplifikasi suatu sistem atau objek yang merepresentasikan hal yang rumit menjadi sederhana dengan segala asumsi-asumsinya.
3 poin penting dalam model yaitu asumsi, representasi, dan simplifikasi.
Contoh dari model ini adalah sebuah pondasi. Pondasi ini dimodelkan dalam bentuk 3D dan modulus elastisitas diasumsikan sama di semua titik, setelah itu di sederhanakan(simplifikasi) dengan menggunakan model 2D.
Modelyang kita buat ini membutuhkan ilmu untuk membangun persamaan aljabar dan memodelkan persamaan dalam komputasi. Maka kita harus berlatih sejak dini untuk menggunakan komputasi. Terdapat aplikasi dari komputasi yaitu diskritisasi, yaitu membuat sesuatu yang kontinu menjadi beberapa titik-titik yang berhingga.
Pertemuan Kelima
Hari, Tanggal : Rabu, 2 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan metode numerik kali ini, topik pembelajarannya adalah aplikasi aljabar yang akan dimodelkan pada sistem pegas. Pak Dai mengatakan bahwa semua masalah dapat dimodelkan, tidak ada permasalahan yang tidak dapat dimodelkan. Model ini kemudian dapat mempermudah kita dalam menyelesaikan masalah tersebut. Salah satu contohnya yaitu menggunakan bahasa pemograman python untuk menyelesaikan masalah. Mengapa menggunakan bahasa python? Karena python merupakan bahasa gratis dan sedang digunakan di dalam industry 4.0 sekarang ini.
Pada pertemuan metode numerik kali ini, asisten dosen menjelaskan mengeian penggunaan pemodelan pada sistem tunggal menjadi sebuah persamaan linear dengan menerjemahkan rumus yang biasa digunakan pada materi pegas menjadi sebuah matriks sehingga mempermudah kemudian untuk mengolahnya. Selain itu, diberikan juga materi mengenai cara pembuatan matriks pegas yang bukan tunggal, yaitu dengan cara menerapkan superposisi matriks. Selanjutnya diberikan penjelasan dan cara penggunaan modul yang dapat digunakan pada python yang mempermudah perhitungan sistem persamaan linear, yaitu numpydan sympy.
Tugas yang diberikan untuk minggu depan adalah membaca buku mengenai motode Runge-Kutta.
Pertemuan Keenam
Hari, Tanggal : Rabu, 9 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan metode nureik kali ini, materi yang diberikan adalah mempelajari cara untuk memecahkan satu set persamaan aljabar. Teknik-teknik menyelesaikan persamaan aljabar adalah:
- metode eliminasi : mengurangi variabel dari persamaan berikutnya, sehingga persamaan akhirnya hanya 1 variable lalu nanti disubstitusi.
- Gauss
- Trial and Error dll
Menurut Pak Dai yang perlu diketahui adalah peran komputer dalam pemodelan. Beliau mngatakan bahwa dalam pemodelan ini logika tetap berasal dari manusia namun komputer membantu mempercepat perhitungan. Maka dari itu kemarin kita mendiskusikan mengenai sebuah pemodelan dari suatu permasalahan menjadi persamaan aljabar.
Kontinu Assumption : contoh dalam satu ruangan dipenuhi oleh oksigen, maka tidak ada ruang hampa dalam ruangan. Seluruh ruangan dipenuhi oleh oksigen dan kita dapat mengukur temperatur dititik manapun dalam ruangan. Formasi dan udara mungkin tidak terlihat tetapi kita harus membayangkannya, karena imajinasi lebih powerful dari pengetahuan.
Model matematis ini nantinya akan berupa persamaan diferensial. Persamaan diferensial muncul akibat permasalahan yang kita hadapi terjadi secara kontinu. Kontinu Assumption jika diberikan gaya maka setiap titik akan merasakan beban sehingga tiap titik akan berdislokasi atau berpindah tempat. Selisih perpindahan tempatnya disebut dengan displacement (u). Perubahan displacement disebut (du) artinya limit ketika delta u menuju 0 tetapi tidak 0. Jadi diferensial itu sangat kecil namun tidak 0.
KUIS
Hari, Tanggal : Rabu, 16 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan kali ini, diberikan kuis yaitu dengan materi solusi persamaan aljabar simultan dan solusi numerik persamaan diferensial (Initial Value Problem). Kemudian kita diperintahkan untuk menuliskan algoritma dan juga hasil dari running program python untuk dua soal, yaitu:
Problem set 2.1 no 6 hal 55
Problem set 7.1 no 2 hal 263
Program python untuk soal di atas adalah sebagai berikut:
Problem set 2.1 no 6 hal 55
from numpy import linalg
import numpy as np
b1 = [0,0,2,1,2]
b2 = [0,1,0,2,-1]
b3 = [1,2,0,-2,1]
b4 = [0,0,0,-1,1]
b5 = [0,1,-1,1,-1]
nmat = np.array ([b1,b2,b3,b4,b5])
print ("Matriks A adalah :")
print (nmat)
cons = np.array ([1,1,-4,-2,-1])
print ("Matriks b adalah :")
print (cons)
jawab = linalg.solve (nmat,cons)
x1val = int(jawab[0])
x2val = int(jawab[1])
x3val = int(jawab[2])
x4val = int(jawab[3])
x5val = int(jawab[4])
print ("Hasil X untuk matkris AX=b adalah :")
print ("x1= ",x1val)
print ("x2= ",x2val)
print ("x3= ",x3val)
print ("x4= ",x4val)
print ("x5= ",x5val)
Problem set 7.1 no 6 hal 263
def dydx(x, y):
return ((x**2 - 4*y))
# Finds value of y for a given x using step size h
# and initial value y0 at x0.
def rungeKutta(x0, y0, x, h):
# Count number of iterations using step size or
# step height h
n = (int)((x - x0)/h)
# Iterate for number of iterations
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of x
x0 = x0 + h
return y
#misalkan :
x0 = 0
y = 1
x = 0.03
h = 0.01
print ('Nilai y untuk x tersebut adalah:', rungeKutta(x0, y, x, h))
UTS
Hari, Tanggal : Rabu, 23 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Untuk kasus A
from math import *
g= 9.81
m1 = eval(input("massa 1:"))
m2 = eval(input("massa 2:"))
m3 = eval(input("massa 3:"))
w1 = eval(input("koef gesek 1:"))
w2 = eval(input("koef gesek 2:"))
w3 = eval(input("koef gesek 3:"))
alpha= eval(input("sudut kemiringan bidang: "))
a = eval(input("besarnya percepatan: "))
b = sin(alpha)
c = cos(alpha)
t1 = m1*g*(b-w1*c) - m1*a
t2 = m2*g*(b-w2*c) + t1 - m2*a
t3 = m3*g*(b-w3*c) + t2 - m3*a
print ("tegang tali 1 adalah: ",t1)
print ("tegang tali 2 adalah: ",t2)
print ("tegang tali 3 adalah: ",t3)
Link video: Penyelesaian Soal UTS 1A
Data yang diinput:
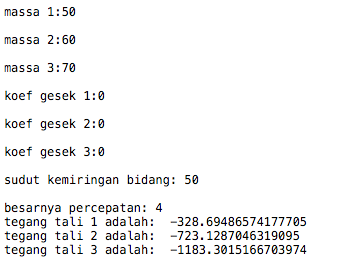
Untuk kasus B
from math import *
from sympy import *
g = 9.81
rho = 1.2 #massa jenis dari udara
dc = eval(input("drag coefficient:"))
area = eval(input("luas(m^2):"))
v1 = eval(input("kecepatan akhir (m/s):"))
M = eval(input("massa mobil (kg):"))
w = eval(input("koefisien gesek:"))
a = eval(input("percepatan (m/s^2):"))
Fg = g*w
f1 = a
for v0 in range (0,v1):
Fdrag = (dc*v0**3/2)/M
atot = f1-(Fdrag+Fg)
t = -(v1)/atot
print ("Percepatan Total (m/s^2):",atot)
print ("Waktu yang diperlukan oleh V1(s):",t)
Link video: Penyelesaian Soal UTS 1B
Data yang diinput:
Video muhasabah diri : Muhasabah Diri
PERBAIKAN UTS
Hari, Tanggal : Jumat, 25 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
BAGIAN A dengan metode runge kutta
import math
import numpy as np
#matrix c & d
C = np.array([[1., 0., 0.],
[-1., 1., 0.],
[0., -1., 1.]], float)
D = np.array([21.37, 14.24, 7.12], float)
n = len(C) #panjang baris C
print('Matriks C :')
print(C,'\n')
print('Matriks C mempunyai ', n , ' baris','\n')
print('Matriks D :')
print(D,'\n')
for k in range(0,n-1): #Metode gauss
for i in range(k+1,n):
if C[i,k]!=0 :
lam = C[i,k]/C[k,k]
C[i,k:n] = C[i,k:n]-(C[k,k:n]*lam)
D[i] = D[i]-(D[k]*lam)
print('matrix C:', '\n', C, '\n')
print('Tegangan Tali adalah:')
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(D[m]-np.dot(C[m,m+1:n],x[m+1:n]))/C[m,m]
print('T',m+1,'=', x[m])
BAGIAN B dengan metode runge kutta
g = 9.81
w = eval(input("koefisien gesek : "))
a = eval(input("percepatan mobil : "))
dc = eval(input("koefisien drag : "))
m = eval(input("massa mobil : "))
t0 = 0
v0 = 0
dt = 1
error = 100
sigmaf = a - g*w #dibagi massa
fs = dc/m #dibagi massa
lst = []
def dvdt(t0, v0):
return sigmaf-(fs*(v0)**(1.5))
while error > 0.005:
k1 = dvdt(t0, v0)
k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1)
k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2)
k4 = dvdt(t0 + dt, v0 + dt * k3)
v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + dt
error = ((v1 - v0) / v1)*100
v0 = v1
lst.append(v1)
waktu = len(lst)
print ("kecepatan maksimal adalah: ", v1, "m/s")
print ("waktu untuk mencapai kecepatan maksimal adalah: ", waktu+1, "s")
Pertemuan kesembilan: Pemodelan Runge Kutta
Hari, Tanggal : Rabu, 6 November 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
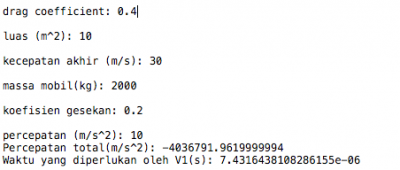
Pemograman dengan metode runge kutta:
g = 9.81
t = float(input("Waktu roket jatuh (s): "))
while t < 0:
print("Waktu (t>0) :")
t = float(input("Waktu roket kembali (s): "))
m = float(input("Massa roket (kg): "))
while m < 0:
print("massa>0.")
m = float(input("Massa roket kembali (kg): "))
dc = float(input("Koefisien drag: "))
while dc < 0:
print("koef drag (>0).")
m = float(input("Koefisien drag kembali: "))
t0 = 0
v0 = 0
step = 0.01
#f(t,v) adalah fungsi (x,y) dimana t diposisikan sebagai x dan v diposisikan sebagai y.
def f(t, v):
return ((m*g-dc*v**1.5)/m)
#rungekutta orde4
def rungekutta(t0, v0, t, step):
n = (int)((t - t0)/step)
v = v0
for i in range(1, n + 1):
k1 = step * f(t, v)
k2 = step * f(t + 0.5 * step, v + 0.5 * k1)
k3 = step * f(t + 0.5 * step, v + 0.5 * k2)
k4 = step * f(t + step, v + k3)
#untuk v baru
v = v + (1/6)*(k1 + 2 * k2 + 2 * k3 + k4)
#untuk t baru
t0 = t0 + step
return v
print("Setelah", t, "s jatuh, kecepatan roket adalah", rungekutta(t0, v0, t, step), "m/s")
Tugas: CFD (mobil)
Hari, Tanggal : Rabu, 20 November 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Landasan Teori
Drag force merupakan gaya kebelakang yang mendorong mundur serta menekan kebawah dan drag force ini disebabkan karena gangguan aliran udara pada bodi kendaraan dan parallel dengan arah angin. Drag force adalah jumlah semua gaya eksternal dalam aliran fluida yang melawan arah gerak objek dan disebabkan oleh aliran turbulen di sekitar benda yang melawan gerak maju objek melalui fluida (gas atau cairan).
Drag force dapat dimanfaatkan menjadi salah satu cara yang efisien untuk meningkatkan kecepatan kendaraan serta menghemat penggunaan bahan bakar. Hal ini dapat terjadi karena jika koefisien drag semakin kecil, maka hambatan udara terhadap mobil semakin kecil, sehingga mobil dapat melaju dengan tenaga dari mesin yang lebih sedikit dan pada akhirnya akan mengurangi pemakaian atau konsumsi bahan bakar mesin mobil.
Secara teori, jika koefisien drag semakin berkurang, maka kecepatan akan semakin meningkat, sesuai dengan persamaan gaya drag yang di mana koefisien drag berbanding terbalik dengan kecepatan. Oleh karena itu, pengaruh tahanan udara yang paling besar terjadi ketika laju kendaraan pada kecepatan yang paling rendah.
Faktor yang sangat penting dalam menentukan kualitas simulasi CFD salah satunya adalah meshing atau griding. Meshing merupakan proses dikritisasi domain fluida yang kontinu yang menjadi domain komputasi yang diskrit sehingga dapat diselesaikan persamaan-persamaan didalamnya dan menghasilkan solusi.
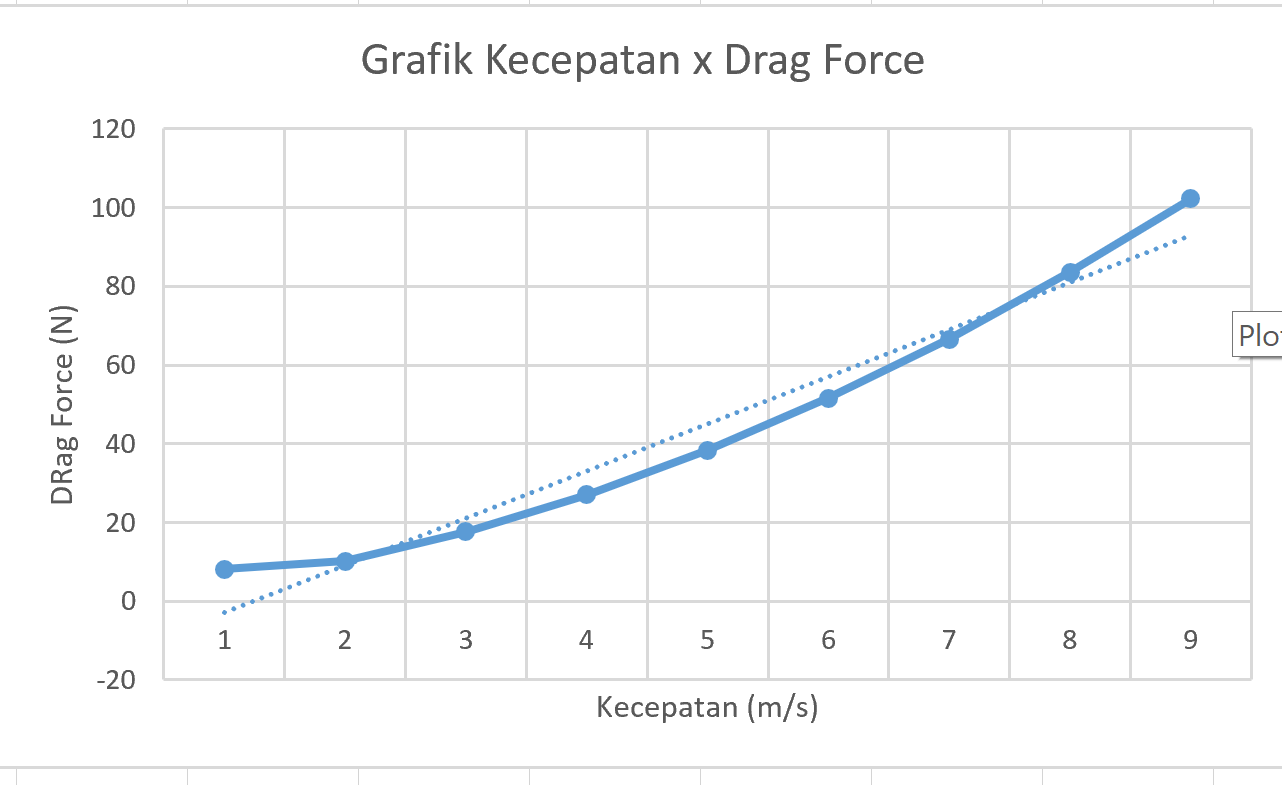
Setelah mengerti penggunaan CFDSOF-NG kami menghitung besarnya drag force dari mobil yang modelnya diberikan, dengan menggunakan aplikasi CFD. Kami mengikuti semua parameter yang telah di berikan mulai dari mesh yang ada sampai jenis aliran udara. Setelah dijalankan, berikut 10 data yang di dapatkan:
kecepatan drag force 10 8.11646 15 10.1848 20 17.6275 25 27.0084 30 38.3158 35 51.53 40 66.6329 45 83.5765 50 102.321
dengan grafik sebagai berikut:
TUGAS ANALISIS GAYA LIFT FORCE DAN DRAG FORCE PADA AIRFOIL (CFDSOF-NG)
Hari, Tanggal : Rabu, 27 November 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada tugas kali ini, kita ditugaskan untuk menganalisis gaya yang terjadi pada sebuah airfoil (sayap pesawat). gaya yang telah dianalisis di hubungkan dengan percobaan sudut yang dibentuk airfoil dengan sumbu normal. Percobaan ini bertujuan untuk menentukan sudut maksimum untuk mendapatkan rasio gaya yang paling baik. Beriukut langkah langkah yang kami lakukan :
1. Mencari referensi airfoil lalu mendesign airfoil tersebut di inventor. 2. Setelah itu kita masukan kedalam CFDSOF-NG untuk di analisis. 3. Akan di dapat sebuah data yang nanti akan di plotting menjadi sebuah grafik. 4. mencari sebuah persamaan yang terbentuk. 5. melakukan optimasi mengunakan pemograman phyton. 6. menarik kesimpulan yang ada.
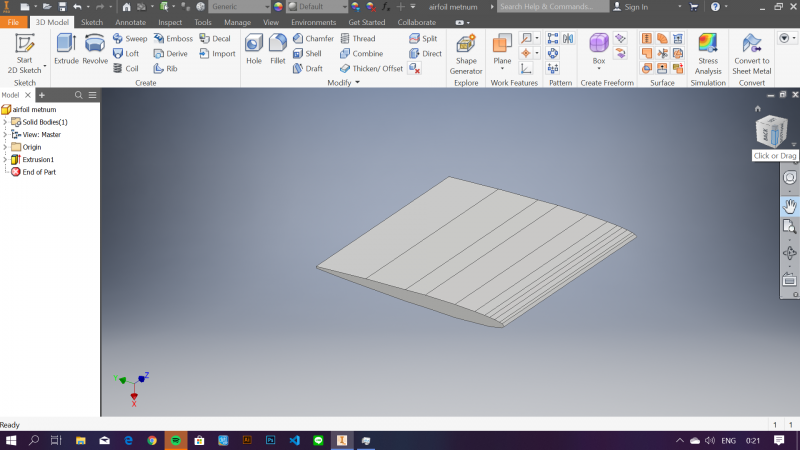
PEMBUATAN AIRFOIL
Berikut airfoil yang kelompok kami buat yang mendapatkan referensi dari NACA 0006.
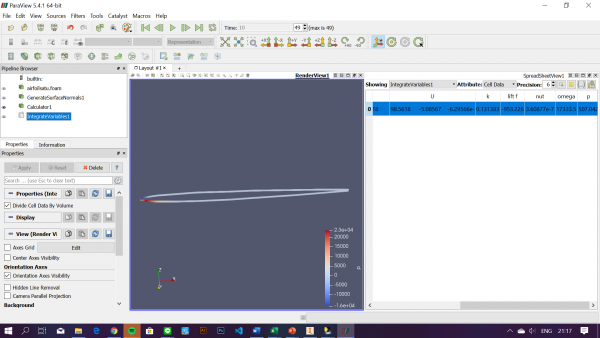
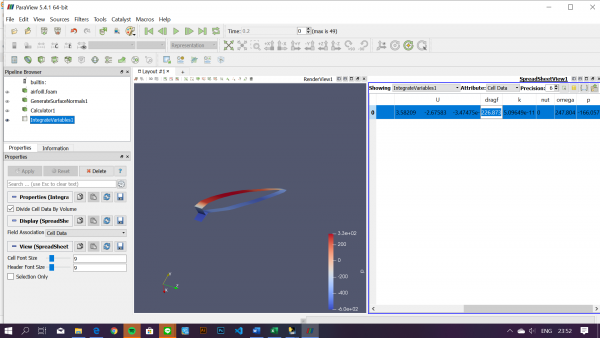
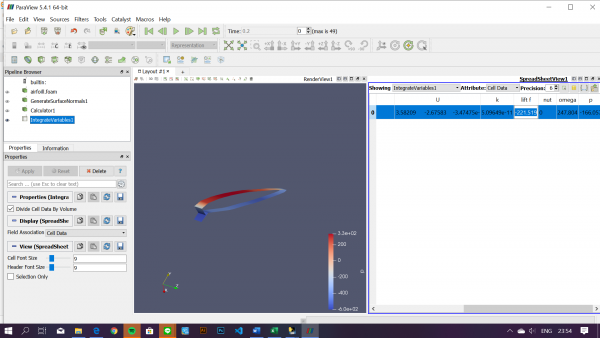
ANALISIS MENGGUNAKAN CFDSOF-NG
MENGOLAH DATA
Setelah melakukan analisis pada CFDSOF-NG, didapatkan data ytang berupa drag forve dan lift foce, berikut data yang telah kami dapatkan :
PEMBUATAN GRAFIK
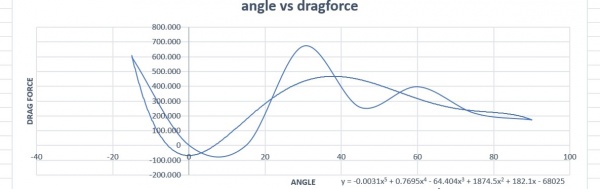
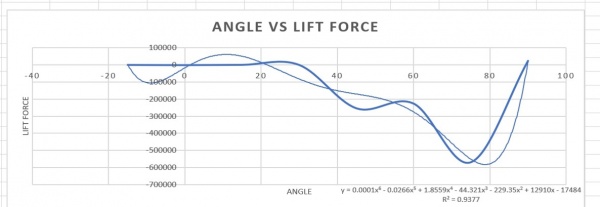
Setelah medapatkan data yang diinginkan, kita dapat memasukan data tersebut kedalam microsoft excel yang dimana nanti akan dibuat sebuah grafik yang menggunakan trend line guna mendapatkan persamaannya. berikut hasil grafik drag dan lift force terhadap sudut yang telah kami buat :
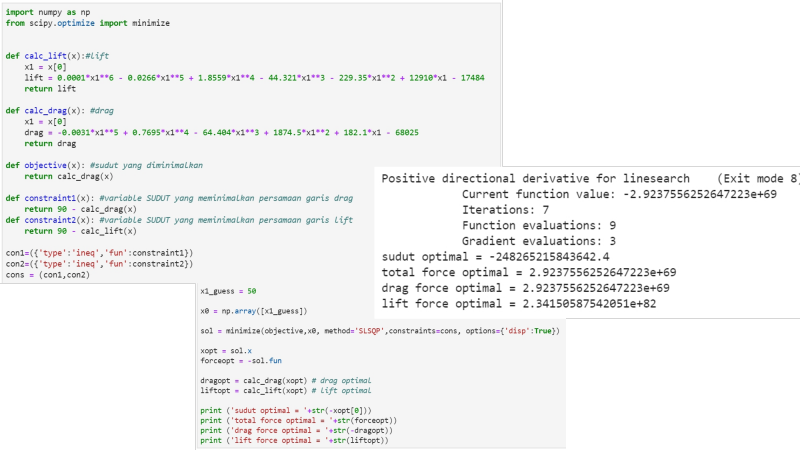
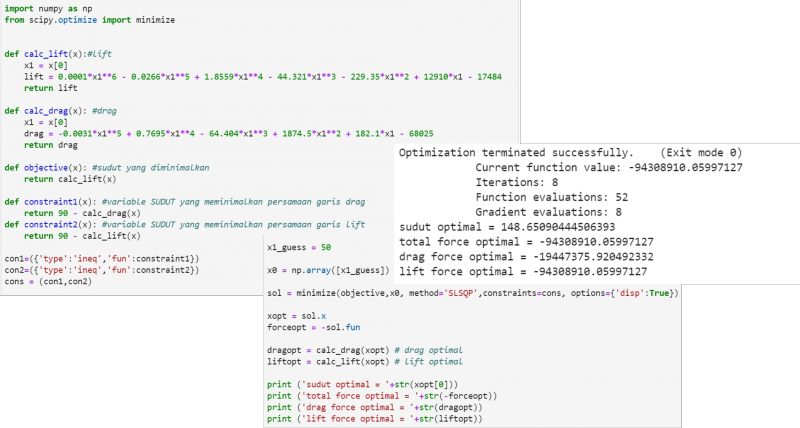
PEMOGRAMAN MENGGUNAKAN PHYTON
Setelah mendapatkan persamaan yang ada pada grafik, kita dapat membuat pemograman untuk melakukan optimasi, berikut optimasinya :
Penjelasan tentang ANN
Hari, Tanggal : Rabu, 11 Desember 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
ANN Adalah sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan.
Backpropagation adalah algoritma pembelajaran untuk memperkecil tingkat error dengan cara menyesuaikan bobotnya berdasarkan perbedaan output dan target yang diinginkan. Backpropagation juga merupakan sebuah metode sistematik untuk pelatihan multilayer.
Arsitektur algoritma backpropagation terdiri dari tiga layer, yaitu input layer, hidden layer dan output layer. Pada input layer tidak terjadi proses komputasi, namun pada input layer terjadi pengiriman sinyal input X ke hidden layer. Pada hidden dan output layer terjadi proses komputasi terhadap bobot dan bias dan dihitung pula besarnya output dari hidden dan output layer tersebut berdasarkan fungsi aktivasi tertentu. Dalam algoritma backpropagation ini digunakan fungsi aktivasi sigmoid biner, karena output yang diharapkan bernilai antara 0 sampai 1.
Algoritma backpropagation adalah sebuah algoritma untuk memperkecil tingkat error dengan menyesuaikan bobot berdasarkan perbedaan output dan target yang diinginkan. Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu : Pengambilan input Penelusuran error Penyesuaian bobot
Steps untuk membuat ANN : Data Preprocessing Add input layer Random w init Add Hidden Layers Select Optimizer, Loss, and Performance Metrics Compile the model use model.fit to train the model Evaluate the model Adjust optimization parameters or model if needed
Terima Kasih telah membaca Wiki saya!
Apabila ada yang ingin disampaikan dapat mengisi kolom komentar dibawah ini!




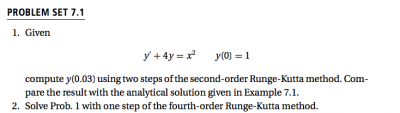

Enable comment auto-refresher