Andika Ridwan Pratama
Contents
Profil
- Nama : Andika Ridwan Pratama
- NPM : 1706986302
- Program Studi : Teknik Mesin
Ringkasan Hasil Pertemuan 1
- Tanggal : 3 September 2019
- Pengajar : Dr. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih M.T.
Materi yang didapatkan pada pertemuan pertama tentu saja diawali dengan penjelasan singkat tentang apa itu Metode Numerik. Dijelaskan bahwa Metode Numerik merupakan metode perhitungan menggunakan kaidah konvergenitas untuk menentukan nilai dari suatu fungsi. perhitungan ini dilakukan berulang-ulang sehingga membutuhkan bantuan alat komputasi agar hasil yang didapat akurat. Pada kelas Metode Numerik ini proses komputasi dilakukan dengan bantuan aplikasi Microsoft Excel.
Kelas Metode Numerik merupakan kelas lanjutan dari Kalkulus, Aljabar Linear, dan Matematika Teknik. Disini kita diajarkan untuk memasukkan ilmu yang didapatkan dari mata kuliah sebelumnya kedalam aplikasi Microsoft Excel agar penghitungan dapat dilakukan secara otomatis. Pada Pertemuan kali ini kita diajarkan untuk mencari nilai dari fungsi Sin(x), Cos(x), dan e^x menggunakan deret Taylor yang telah dipelajari sebelumnya.
Ringkasan Hasil Pertemuan 2
- Tanggal : 10 September 2019
- Pengajar : Dr. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih M.T.
Materi yang didapatkan pada pertemuan kedua ini adalah tentang tingkatan bahasa mesin, dan pseudocode. Dijelaskan bahwa tingkatan bahasa mesin untuk yang paling rendah adalah bahasa Binary atau Biner. bahasa ini hanya berisi angka 1 dan 0 dan kombinasi dari keduanya. bahasa ini sangat sulit untuk dipahami oleh manusia karena memiliki kombinasi yang amat banyak. oleh karena itu dibuatlah bahasa pemrograman yang disebut dengan compiler. compiler disini berfungsi untuk menterjemahkan bahasa manusia ke dalam bahasa biner yang dimengerti oleh mesin, agar kita lebih mudah untuk menuliskan suatu program. Pseudo Code adalah adalah perintah yang dituliskan untuk menjalankan suatu fungsi.
Berikut merupakan contoh Pseudo Code untuk mencari nilai sin
I = r ; err = 1
suku = x
sin = suku
while err > 1e-7
{ ratio = -x^2/((2*I)*(2*I+1))
suku = suku*ratio
err = abs(suku/sin)
sin = sin + suku
I = I+1 }
Ringkasan Hasil pertemuan 3
- Tanggal : 29 Oktober 2019
- Pengajar : Dr. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih M.T.
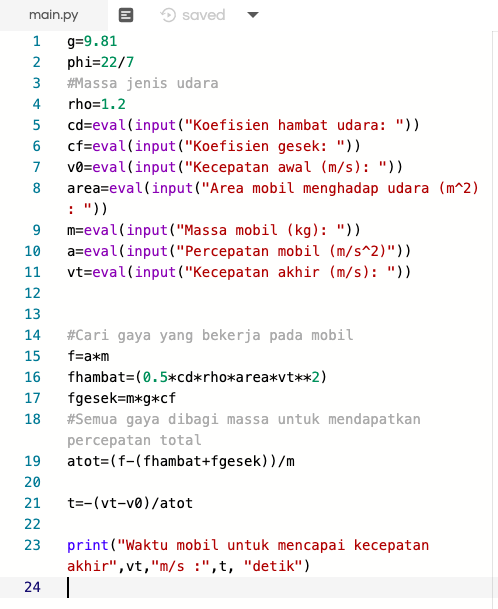
diberikan tugas untuk membuat persamaan kecepatan maksimal pada mobil, dan waktu untuk mencapai kecepatan tersebut. diasumsikan kendaraan memiliki 3 gaya-gaya yang mempengaruhi perhitungan
F = m*a F gesek = m*g*cf F hambat = 0.5*cd*rho*area*vt^2 Dengan membagi ketiga gaya tersebut dengan massa didapatkan percepatan total
v'(t)= (F - (F gesek + F hambat))/m
Kemudian apabila disubsitusikan ke turunan dari kecepatan terhadap waktu
v'(t)= v(t)/t
dapat dicari waktu dengan cara membagi kecepatan dengan percepatan total, dimana percepatan total adalah turunan dari kecepatan terhadap waktu
t= v(t) / ((F - (F gesek + F hambat))/m)
Pseudo
Untuk variable yang digunakan untuk simulasi berupa:
Power= 500 KW
Massa= 1500 kg
Percepatan gravitasi= 9.81 m/s^2
Koefisien gesek= 0.7
Massa jenis= 1.2 kg/m^2
Area= 10 m^2
Koefisien drag= 0.2
Ringkasan Hasil Pertemuan 12 November 2019
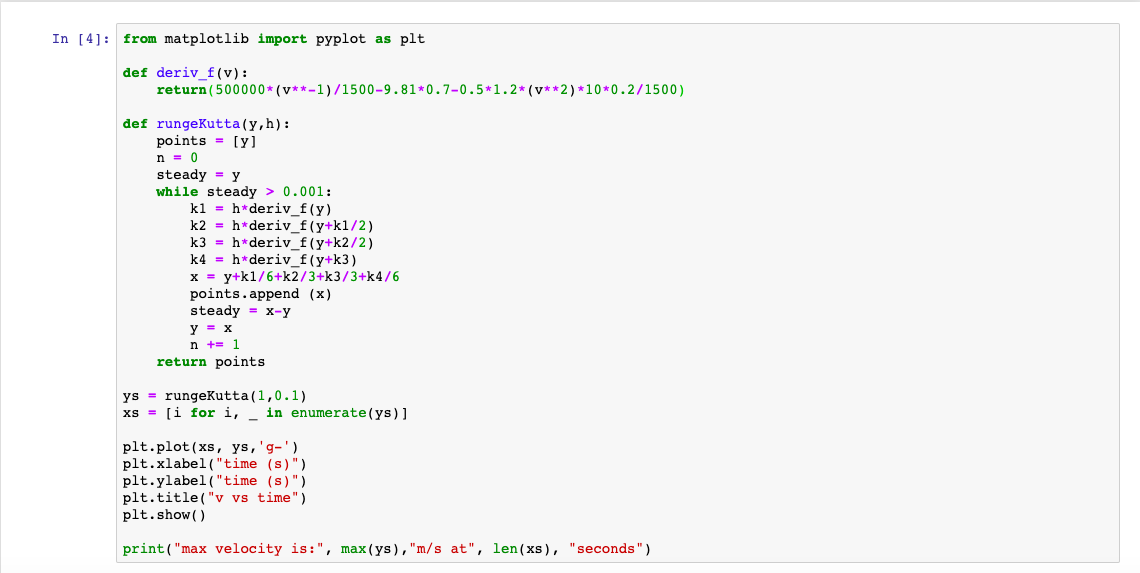
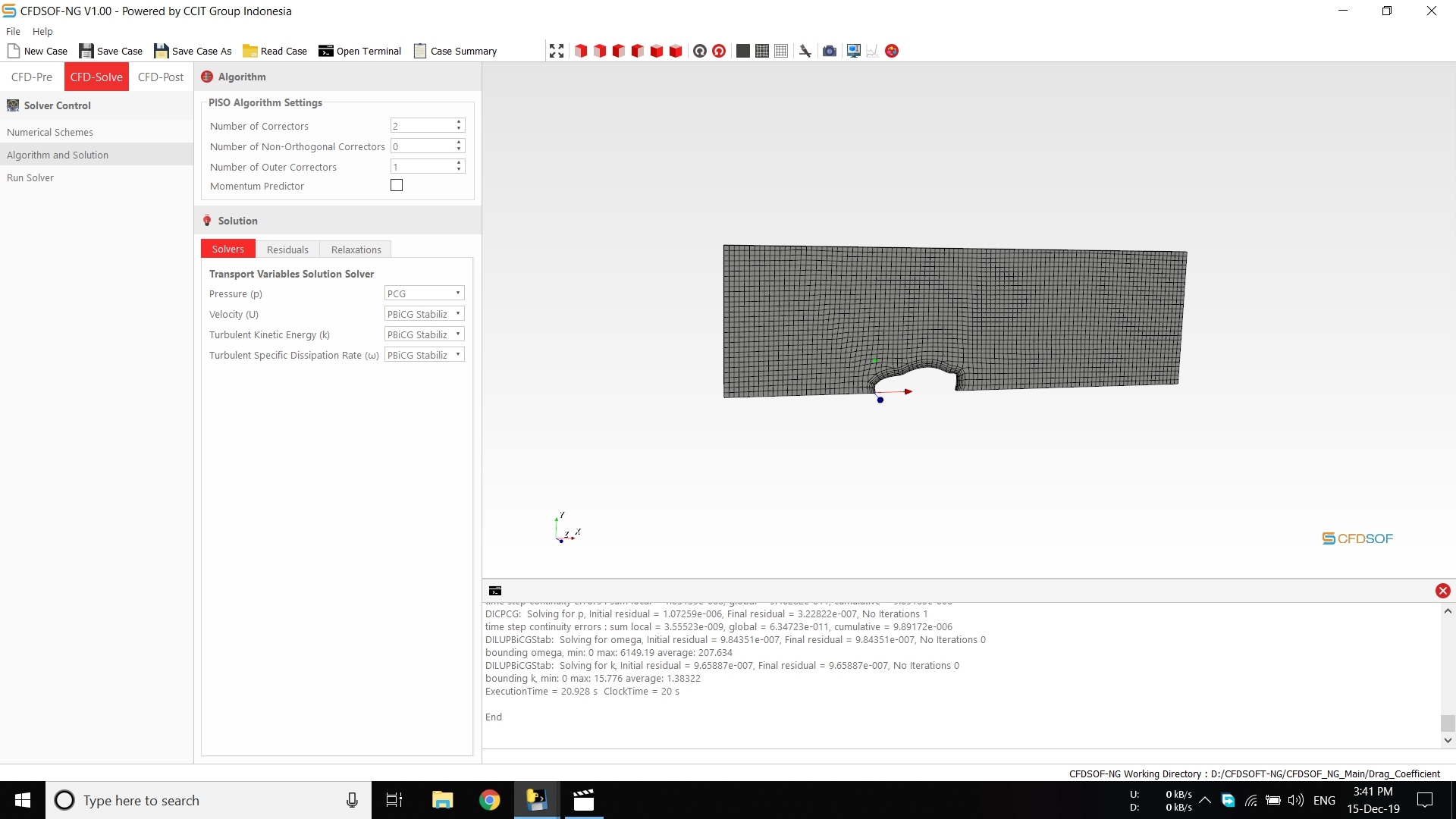
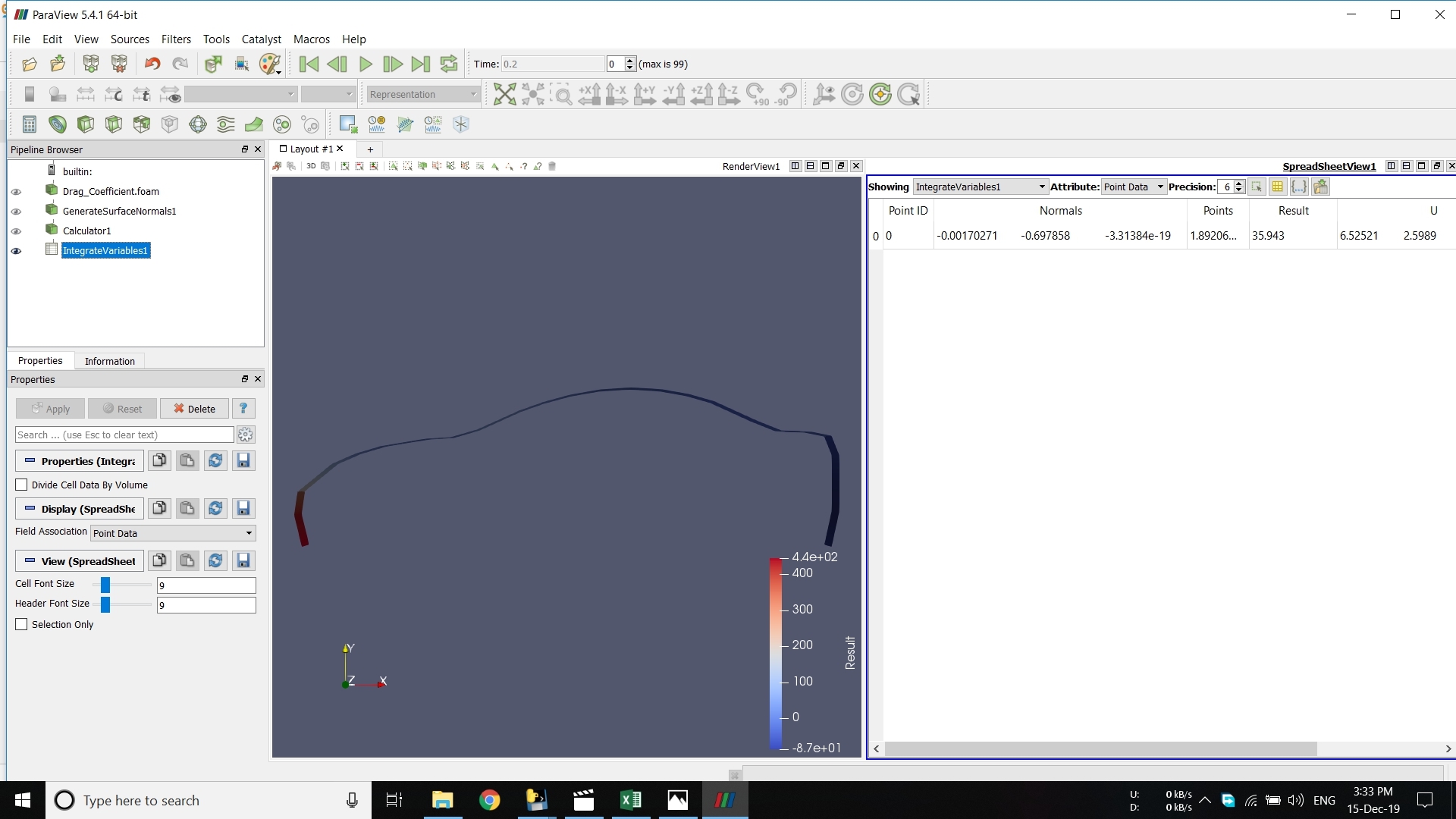
Pada pertemuan ini kami diajarkan cara menggunakan CFDSOF khususnya cara menganalisis suatu fluida yang berjalan pada suatu mobil. Hasil dari simulasi ini kemudian dijadikan tugas kelompok dimana mencari rumus persamaan gaya hambat dari kecepatan.
Pada tugas kali ini kami ditugaskan untuk mencari rumus dari gaya hambat menggunakan simulasi CFDSOF. Gaya hambat adalah gaya yang melawan benda saat melewati fluida seperti cairan atau gas. Pada kali ini kami menganalisis gaya hambat sebuah mobil saat melewati udara.
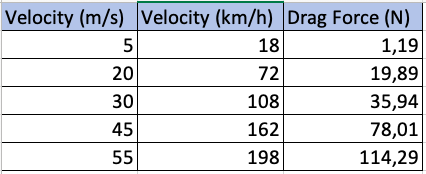
Simulasi CFDSOF Untuk mendapatkan gaya hambat untuk setiap kecepatan kami melakukan simulasi di CFDSOF. Untuk variabel kecepatannya ditentukan 5 variabel yaitu:
5 m/s atau 18 km/h untuk rata-rata kecepatan rush hour dalam kota
20 m/s atau 72 km/h untuk rata-rata kecepatan non-rush hour dalam kota
30 m/s atau 108 km/h untuk rata-rata kecepatan pada tol
45 m/s atau 162 km/h untuk kecepatan maksimal mobil biasa
55 m/s atau 198 km/h untuk kecepatan maksimal mobil sport
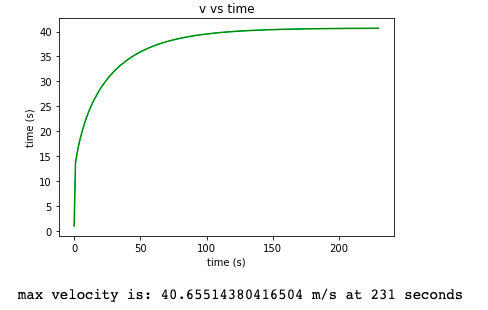
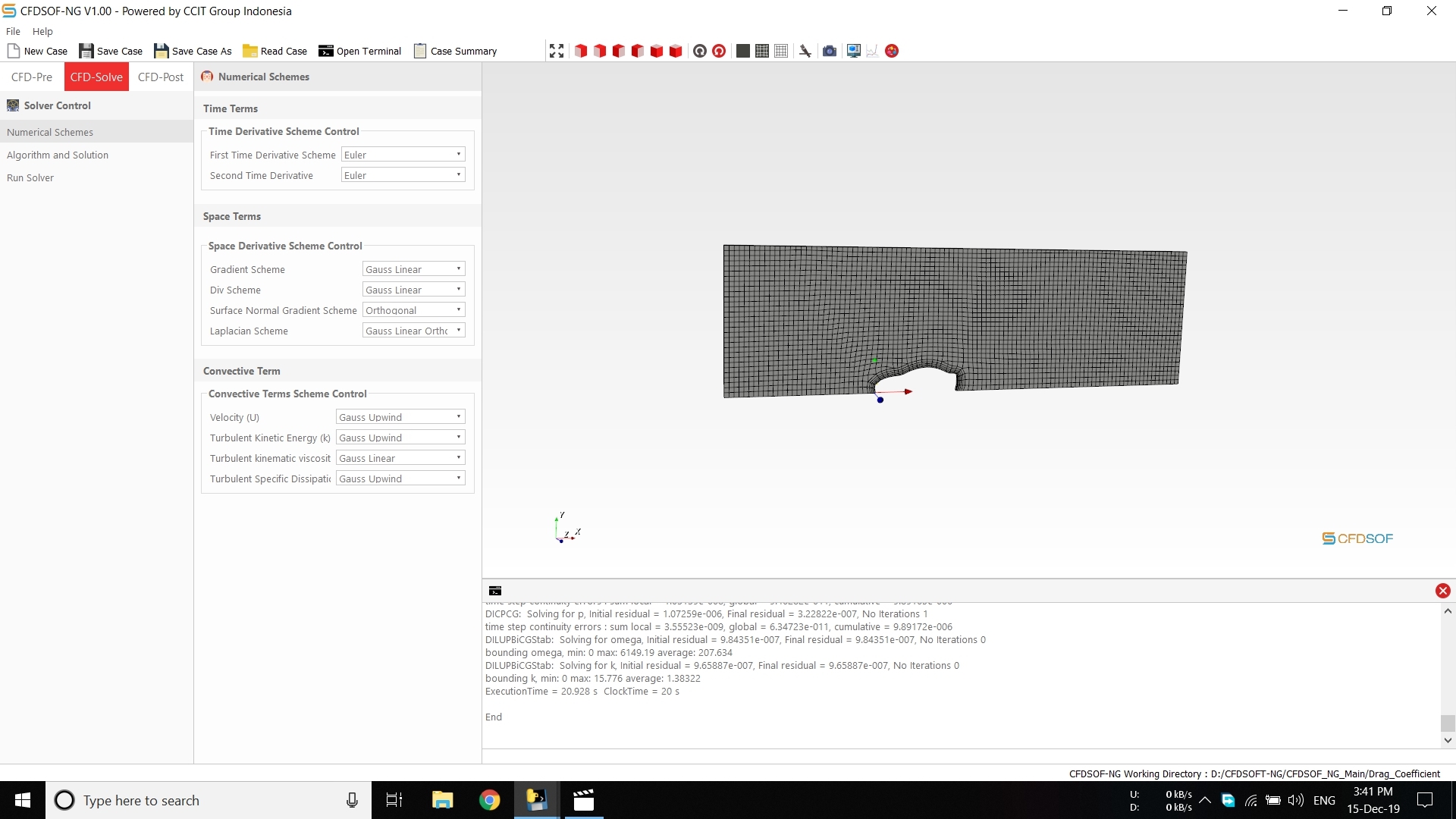
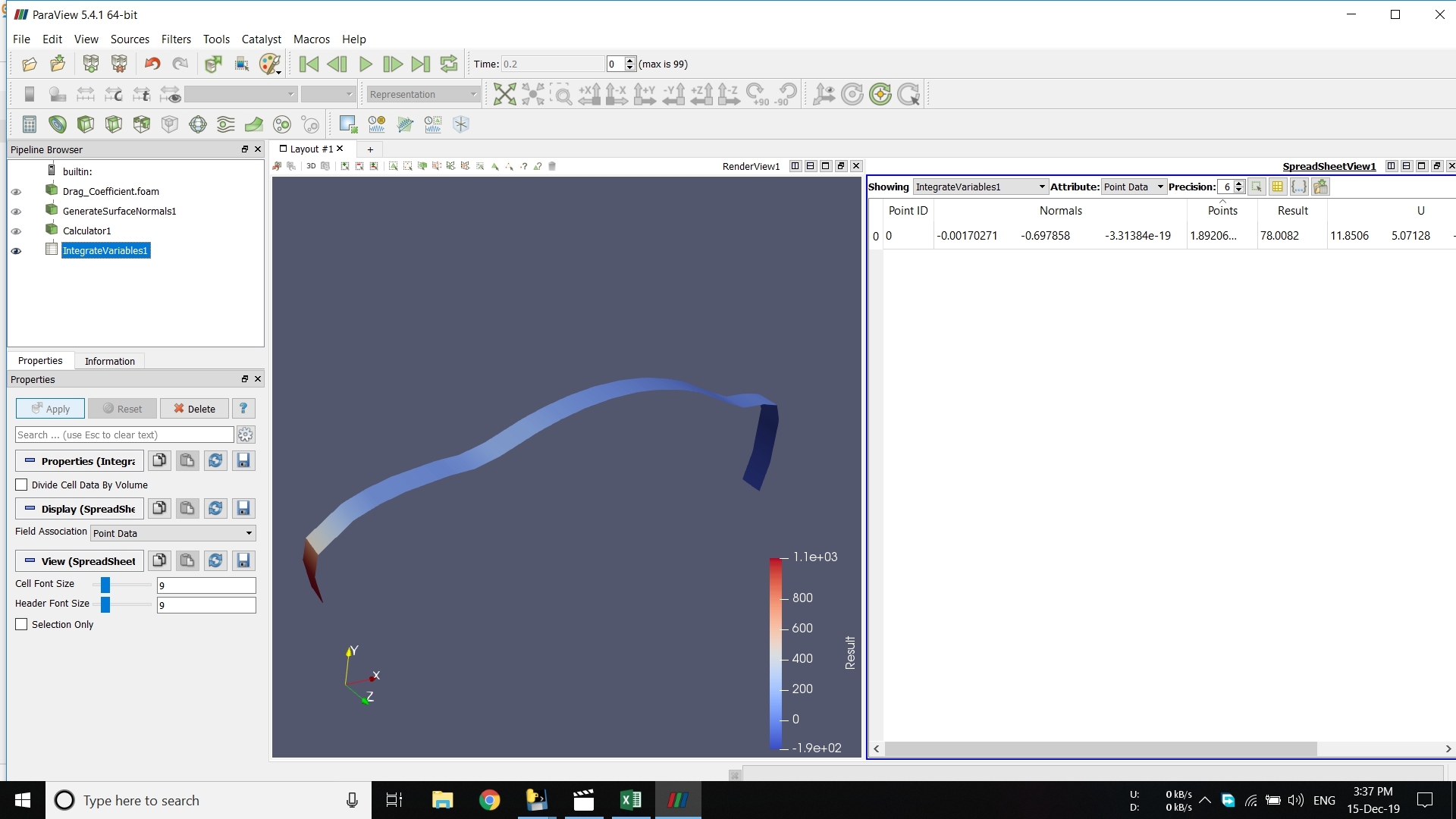
Berikut adalah proses simulasi yang kami lakukan dengan aplikasi CFDSOF
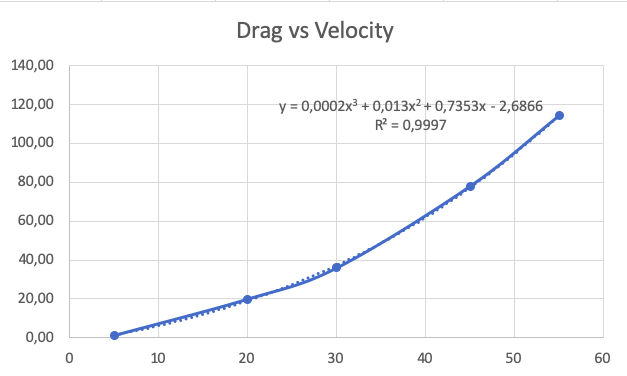
Dari kurva diatas, didapatkan bahwa rumus untuk gaya drag adalah y = 0,0002x3 + 0,013x2 + 0,7353x - 2,6866
Dengan y adalah gaya drag dan x adalah kecepetan, sehingga didapatkan rumus akhir Fd = 0,0002v3 + 0,013v2 + 0,7353v - 2,6866
Ringkasan Hasil Pertemuan 26 November 2019
Airfoil memiliki karakteristik aerodinamis dan merupakan benda yang sering digunakan contohnya pada pesawat. Thrust pada pesawat berpengaruh pada effisiensi aerodinamis, maka dari itu dibutuhkan Cl/Cd yang kecil. Cl dan Cd tergantung pada angle of attack dari airfoil. Kali ini kita menggunakan airfoil NACA 0012 sebagai objek simulasi. Diasumsikan fluida udara yang melewat air foil steady flow dan incompressible dan simulasi CFD dalam kondisi adiabatic agar simulasi dapat dilakukan dengan lebih mudah.
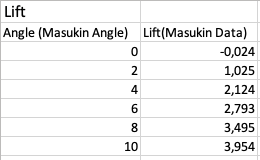
Kemudian Airfoil yang digunakan dilakukan variasi pada 6 angle of attack yang berbeda berupa:
0
2
4
6
8
10
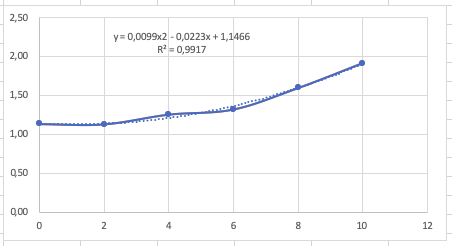
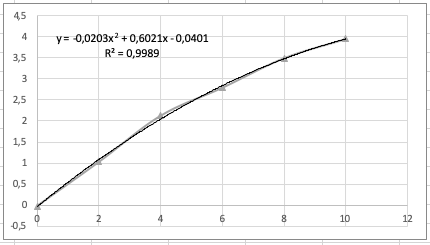
Simulasi CFD SOF Dilakukan simulasi airfoil pada 6 sudut tersebut pada aplikas CFD-SOF kemudian didapatkan hasil data sebagai berikut:
Dengan mencari rumus kurva pada excel, didapatkan rumus drag berupa y = 0,0099x2 - 0,0223x + 1,1466 dan rumus lift berupa y = -0,0203x2 + 0,6021x - 0,0401.
Optimasi Dari kedua rumus diatas kemudian dimasukkan dalam program python dibawah ini:
import numpy as np
from scipy.optimize import minimize
def calc_drag(x):#drag
x1 = x[0]
drag = 0.0099*x1**2-0.0223*x1**1+1.1466
return drag
def calc_lift(x): #lift
x1 = x[0]
lift = -0.0203*x1**2+0.6021*x1**1-0.0401
return lift
def objective(x): #volume yang diminimalkan
return calc_drag(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x
forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal
liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(-xopt[0]))
print ('total force optimal = '+str(forceopt))
print ('drag force optimal = '+str(-dragopt))
print ('lift force optimal = '+str(liftopt))
# In[10]:
import numpy as np
from scipy.optimize import minimize
def calc_drag(x):#drag
x1 = x[0]
drag = 0.0099*x1**2-0.0223*x1**1+1.1466
return drag
def calc_lift(x): #lift
x1 = x[0]
lift = -0.0203*x1**2+0.6021*x1**1-0.0401
return lift
def objective(x): #volume yang diminimalkan
return calc_lift(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x
forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal
liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(-forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))
Kemudian setelah program dijalan didapatkan hasil sebagai berikut:
Optimization terminated successfully. (Exit mode 0)
Current function value: 1.1340421717179265
Iterations: 5
Function evaluations: 15
Gradient evaluations: 5
sudut optimal = -1.1262713580043062
total force optimal = -1.1340421717179265
drag force optimal = -1.1340421717179265
lift force optimal = 0.6122776950656171
Optimization terminated successfully. (Exit mode 0)
Current function value: -128.89494468045336
Iterations: 7
Function evaluations: 24
Gradient evaluations: 7
sudut optimal = 95.86991386912578
total force optimal = -128.89494468045336
drag force optimal = 90.00000073492711
lift force optimal = -128.89494468045336
Ringkasan Hasil Pertemuan 3 Desember 2019
Pada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan. Kemudian dijelaskan mengenai neural network yaitu sebuah jaringan neuron yang berfungsi seperti otak manusia, dimana setelah dilatih dapat memprediksi hal-hal.