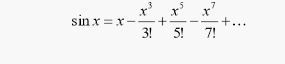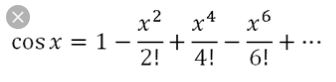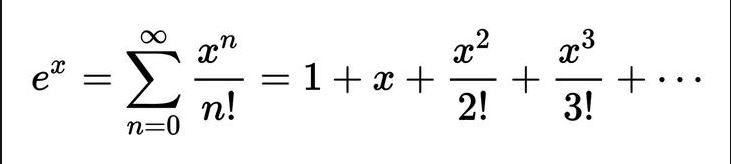Gede Titanandana Andrayuga Pratama

---

Profil

Nama : Gede Titanandana Andrayuga Pratama NPM : 1706036495

Pertemuan 1 (3 September 2019)

Metode Numerik adalah operasi memformulasikan persamaan matematika. Karena batasan kemampuan penghitungan manusia dan kalkulator sederhana maka penghitungan numerik menggunakan komputasi. Salah satu komputasi paling sederhana menggunakan Microsoft Excel. Dengan komputasi dapat melakukan penghitungan dengan efisien dan akurat. Pada materi kelas ini formulasi yang digunakan yaitu menghitung deret taylor dari sin (phi/7). Deret Taylor ini untuk mengakpromisasikan nilai fungsi dengan jumlah dari turunan yang tak berhingga, dalam kasus ini dicari nilai sin (phi/7). Dalam menghitung fungsi ini terdapat beberapa konstanta yaitu :

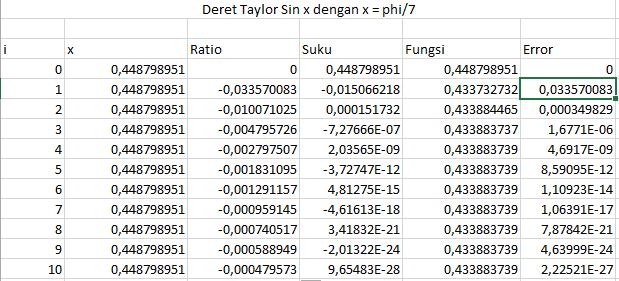
i = turunan ke-i

x = phi/7

Ratio = suku n / suku n-1 yang dimasukan dengan rumus =-1*(Nilai X)^2/((2*Nilai i)*(2*Nilai i + 1))

Suku = Dimasukan dengan rumus = Suku ke n*Rasio pada nilai i

Fungsi = Dimasukan dengan rumus =Fungsi ke n-1 + Suku ke n

Error = Dimasukan dengan rumus =ABS(suku ke n/fumgsi ke n-1

Rumus Taylor Series

Rumus Taylor Series Sin (x)

Berdasarkan hasil komutasi di tabel maka nilai sin(phi/7) = 0,43388

Tugas 1

1) Akpromisasikan nilai cos(phi/7)

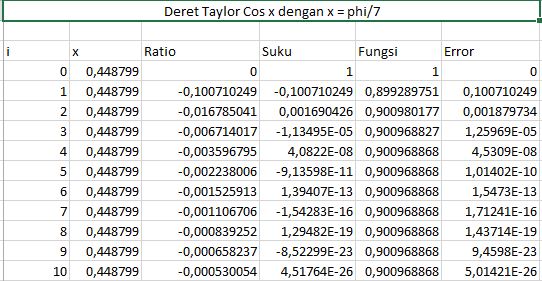
Melihat dari deret taylor cox (x) maka rationya =-1*(Nilai X)^2/((2*Nilai i)*(2*Nilai i - 1))

Berdasarkan tabel maka nilai cos (phi/7) = 0,90097

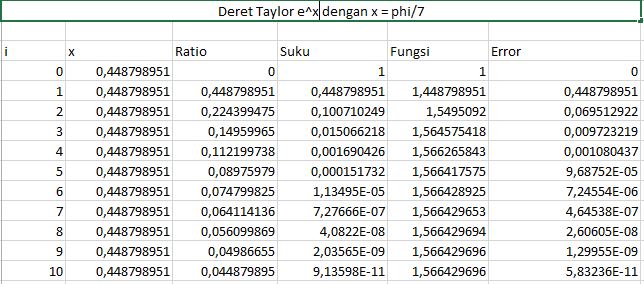
2) Akpromisasikan e^(phi/7)

Melihat dari deret taylor e^x maka rationya = Nilai x / Nilai i

Berdasarkan tabel maka nilai e^(phi/7) = 1,5664

Pertemuan 2 (10 September 2019)

Bahasa pemograman adalah media instruksi komputer untuk menjalankan perintah yang diberikan. Bahasa pemograman paling rendah yaitu binary yang hanya terdiri dari 0 dan 1. Namun untuk menerjemahkan bahasa manusia ke bahasa binary dibutuhkan mesin penerjemah yang disebut complier. Pseudocode sendiri berarti kode imitasi karena tidak dapat diterjemahkan complier namun pseudocode ini menggunakan bahasa manusia sehingga dapat dimengerti langsung. Pseudocode memberikan garis besar instruksi dan dimana dapat menjadi acuan untuk membuat bahasa pemogramannya

Contoh pseudocode , pseudocode sin x

I = r ; error = 1

suku = x

sin = suku

while error > 1e^-7

{

ratio = -x^2/((2^I)*(2+1*I))

suku = suku*ratio

err = abs(suku/sin)

sin = sin + suku

I = I+1

}

Pertemuan 3 (17 September 2019)

Pertemuan kelas hari ini membahas turunan numerik. Turunan numerik digunakan dengan komputasi untuk persamaan kompleks. Hampiran turunan fungsi f(x) dalam bentuk tabel. Terdapat tiga jenis turunan numerik yaitu maju, mundur dan center. Turunan Center digunakan apabila nilai h sama, untuk turunan maju dan turunan mundur digunakan jika tingkat keakuratan yang sama

Turunan Maju

Turunan Mundur

Turunan Center

Pertemuan 4 (24 September 2019)

Pertemuan kali ini membahas rood finding algorithm atau algoritma pembuat nol fungsi. Root finding algorithm dibagi menjadi secant method, bisect method dan newton rhapsodian method

Secant Method : menggunakan garis secan untuk mengaproksimasi nilai sebuah fungsi

Bisect Method : metode pencarian akar-akar untuk fungis yang kontinu

Newton Rhapsodian Method : pendekatan satu titik untuk mencari akar dari suatu fungsi f(x)

Pertemuan 5 (1 Oktober 2019)

Pertemuan sekarang membahas error dan persamaan banyak. Error dibagi menjadi round error, truncation error, dan range error

Round error : Pembulatan angka menjadi dasar kesalahan

Truncation error : Pemotongan suku rumus approksimasi menjadi pemicu kesalahan

Range error : Kesalahan akibat nilai hasil komputasi melampaui batas oleh komputer

Pertemuan 6 (29 Oktober 2019)

Materi hari ini yaitu governing equation. governing equation yaitu persamaan matematis untuk penyelesaian matematis. Pada governing equation kita membuat parameter - parameter dan bagimana kaitan antar parameternya. Tujuan memahami governing equation dari permasalahan sebelum memasukan ke komputasi karena untuk melakukan komputasi dilakukan pengubahan persamaan menjadi bashasa pemograman namun kaitan antar parametrernya sama. Contoh kasus yang diberikan di kelas yaitu menganalisis gaya - gaya pada mobil dengan governing equation sebagai berikut :

Sigma F = m.a

F propulsi - F gaya gesek ban - F gesekan aerodinamik =- m.a

Torsi : jari jari ban - Koefisien gesek ban x Gaya normal - 0.5 x Luas frontal area x koefisien gesek x kecepatan mobil^2 = m.a