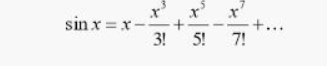Hario Gibran
Contents
Profil
- Nama : Hario Gibran
- NPM : 1706036362
Pertemuan ke-1, 3 September 2019
Oleh : Dr. Ahmad Indra Siswantara dan Dr. Engkos Achmad Kosasih
Pada pertemuan pertama mata kuliah metode numerik, kami dijelaskan bahwa banyak penyelesaian matematik dapat diselesaikan dengan menggunakan teknik metode numerik. Karena tidak semua permasalahan matematik dapat diselesaikan menggunakan kalkulator yang sederhana, maka digunakan metode numerik.
Untuk mendapat nilai log x, ln(x+2), atau ln(x) perlu proses yang panjang dan rumit jika dilakukan secara manual. Untuk mempermudah hal tersebut, ilmu yang dipelajari dalam metode numerik yaitu Deret Taylor atau Deret MacLaurin.
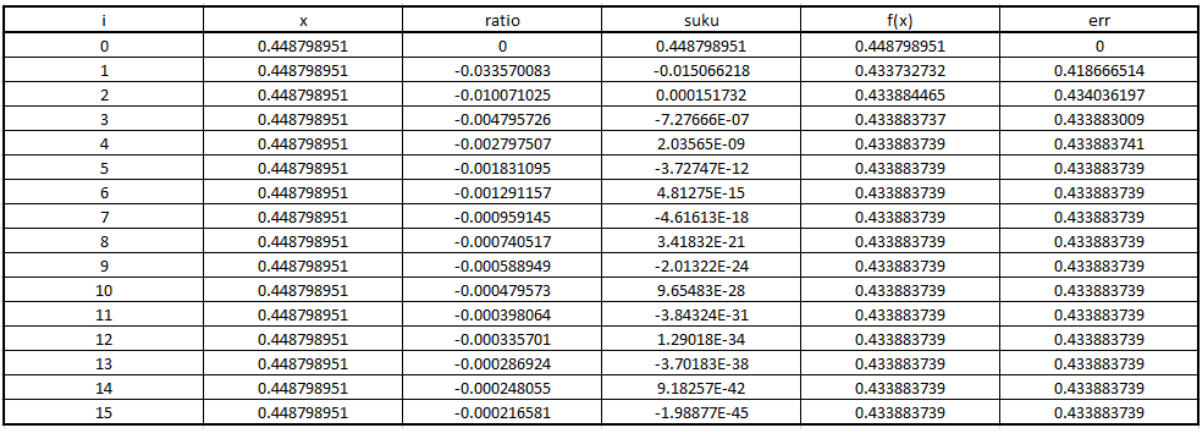
Pada pertemuan kali ini, kami mahasiswa ditugaskan untuk mencari nilai dari sin(pi/7). Berikut penyelesaiannya :
Pertemuan ke-2, 10 September 2019
Pada pertemuan kali ini, mahasiswa diberi penjelasan tentang pseudocode. Pada dasarnya, pseudocode merupakan suatu bahasa yang memungkinkan programmer untuk berpikir terhadap permasalahan yang harus dipecahkan tanpa harus memikirkan syntax dari bahasa pemrograman yang tertentu. Tidak ada aturan penulisan syntax di dalam pseudocode. Jadi pseudocode digunakan untuk menggambarkan logika urut-urutan dari program tanpa memandang bagaimana bahasa pemrogramannya.
Lalu pada pertemuan ini kami diminta membuat pseudocode untuk menemukan nilai dari sin(x), cos(x), dan e^x.
Pertemuan ke-3, 17 September 2019
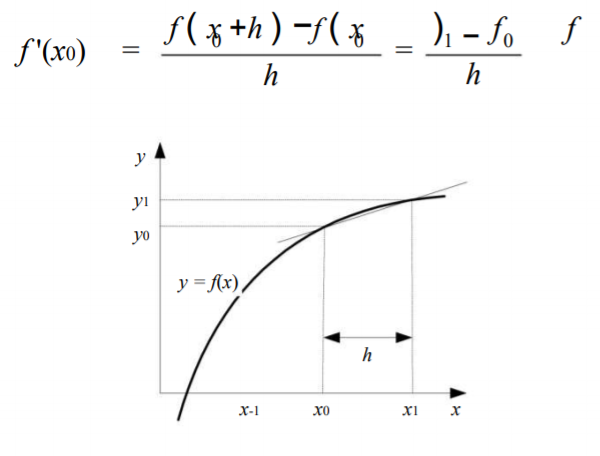
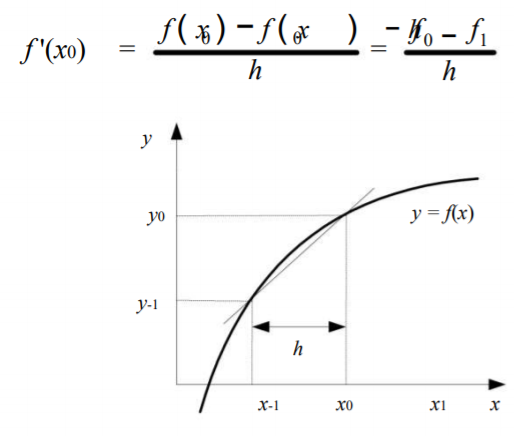
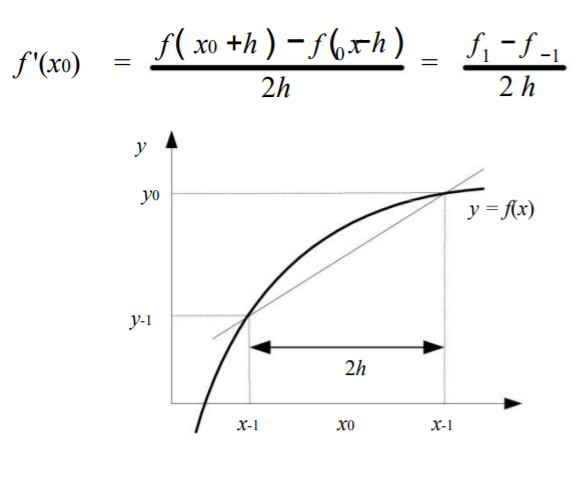
Pada pertemuan kali ini diberi penjelasan mengenai turunan numerik. Persoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Dijelaskan juga bahwa ada 3 pendekatan dalam menghitung turunan numerik, diantaranya:
Pertemuan ke-4, 24 September 2019
Pada pertemuan kali ini kami dijelaskan mengenai root-finding algorithm. Root-finding algorithm ada 3, yaitu:
1. Secant Method yaitu metode mencari persamaan yang ekivalen dengan rumus turunan fungsi,
2. Bisection Method yaitu algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x)=0 dengan f(x) merupakan fungsi kontinyu.
3. Newton-Raphson Method adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x mempunyai turunan.
Pertemuan ke-5, 1 Oktober 2019
Pertemuan kali ini mahasiswa dijelaskan mengenai persamaan banyak dan error. Ada 3 macam error yang dijelaskan di kelas, diantaranya:
1. Round off error yaitu kesalahan pada pembulatan. Dimana aturan pembulatan yang sering diterapkan adalah sebagai berikut: Bila digit yang akan dibulatkan kurang dari 5, maka digit ini dihapus saja Bila digit yang akan dibulatkan lebih atau sama dengan 5 maka digit didepannya ditambah satu kemudian digit ini dibuang. Contoh : 5.34423, 5.34334 keduanya dibulatkan ke 5.34
6.34546 dibulatkan ke 6.35
2. Truncation error yang merupakan kesalahan pemotongan terjadi ketika suatu rumus komputasi disederhanakan dengan cara membuang suku yang berderajat tinggi.
3. Range error, setiap komputer memiliki keterbatasan dalam jangkauan representasi angka, misalnya angka presisi-tunggal (single precision) sekitar 10^+37 dan presisi-ganda (double precision) sekitar 10^+308.