Fadhlan Prabancana

Profil

Nama: Fadhlan Prabancana

NPM: 1706036274

Jurusan: Teknik Mesin

MEETING 1

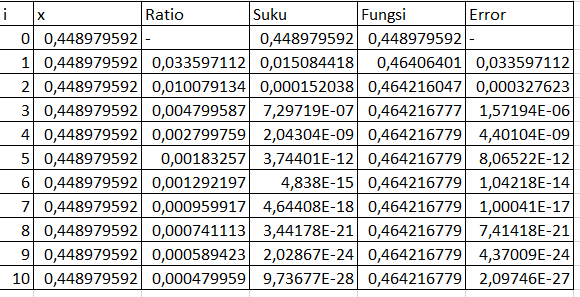
Dalam pertemuan pertama kami mendapatkan gambaran mengenai pentingnya metode numerik. kamipun juga diingatkan kembali mengenai peraturan angka penting, presisi, tes rasio serta deret Taylor dan Maclaurin. Lalu kami melakukan praktik menggunakan excel.

MEETING 2

Pseudocode adalah deskripsi dari algoritma pemrograman komputer yang menggunakan konvensi struktural dari suatu bahasa pemrograman, dan ditujukan agar dapat dibaca oleh manusia dan bukan oleh mesin.

contoh yang dipelajari di kelas

soal:

F(x)=sinx =x-1/6x^3+1/120x^5 i=r; error=1

suku=x

sin= suku

while error>1e^-7

Ratio= -x^2/(2*1)/(2*i+1)

suku=suku *ratio

error= abs(suku/sin)

sin=sin + suku

i=i+1

MEETING 3

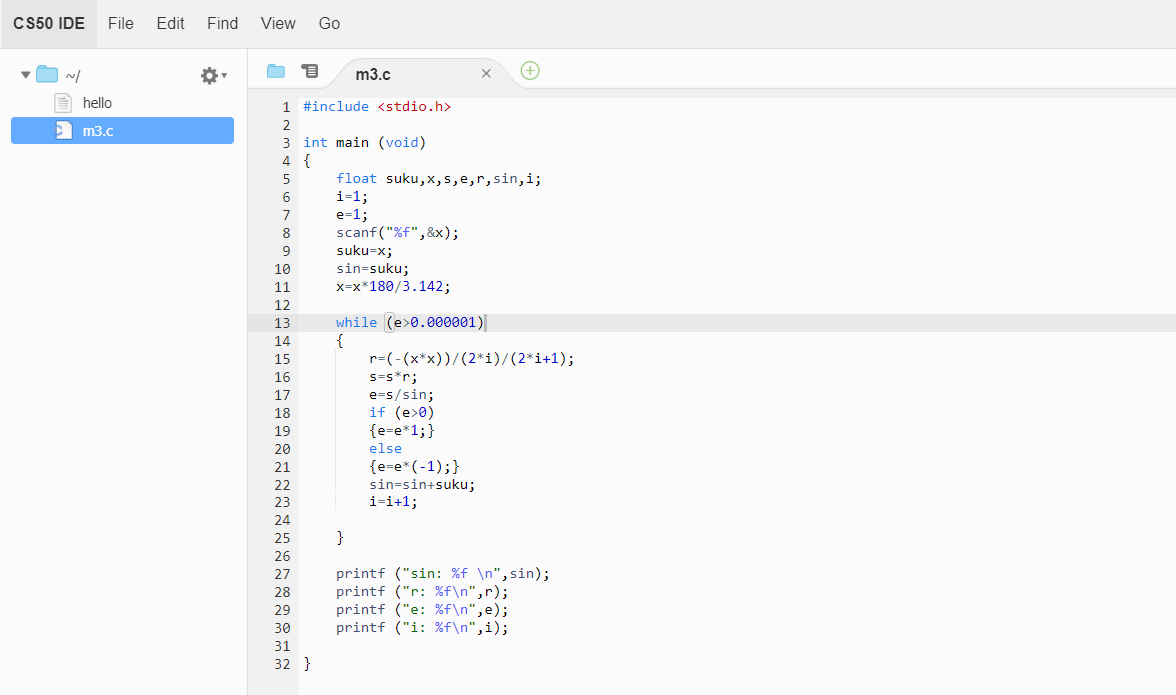
Pada pertemuan ini kami belajar menjadikan pseudocode di meeting 2 ke dalam C++

MEETING 1 After Mid

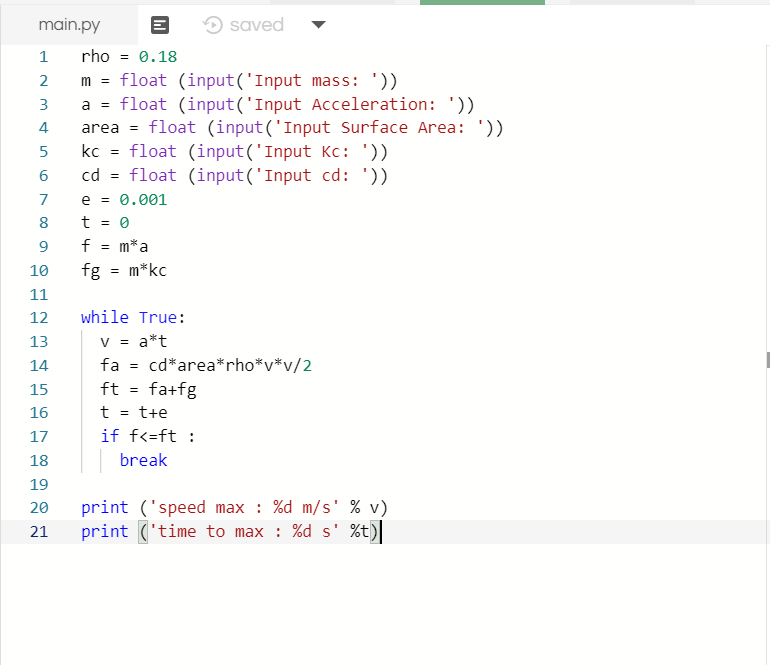
Python adalah bahasa pemrograman interpretatif multiguna dengan filosofi perancangan yang berfokus pada tingkat keterbacaan kode.

Tugas: Menghitung V maks dan T saat V maks mobil

Tugas 1

Optimasi

Airfoil Airfoil adalah bentuk dari suatu sayap pesawat yang dapat menghasilkan gaya angkat (lift) atau efek aerodinamika ketika melewati suatu aliran udara.

Cara Kerja Sayap Udara yang mengalir diatas sayap lebih cepat dari udara yang mengalir dibawah sayap, sehingga tekanan udara diatas pesawat lebih rendah. 

Thrust yang dibutuhkan untuk menerbangkan suatu pesawat sebanding dengan efisiensi aerodinamisnya, Cl/Cd (Anderson, 2012). Semakin sedikit thrust yang dibutuhkan, semakin hemat pengeluaran energinya, sehingga nilai Cl/Cd menjadi penting dalam desain suatu pesawat.

Konstanta drag total merupakan jumlah dari 2 komponen, yaitu profile drag(akibat gesekan dan perbedaan tekanan), dan induced drag. Induced drag ini perbanding kuadrat dengan konstanta lift. Dengan Cd yang berbanding lurus dengan Cl^2, maka pada suatu titik, Cl/Cd akan mencapai titik maksimal, kemudian turun. Sudut optimal didefinisikan sebagai sudut dengan Cl/Cd maksimum untuk free stream velocity tertentu.

Metode Optimasi Golden Section Golden section method merupakan modifikasi dari bisection method untuk mencari nilai optimum dari suatu kurva dalam range tertentu. Cara kerja Golden Section Method adalah dengan membatasi range kita dengan nilai minimum dan maksimum, a dan b. Kemudian kita mendefinisikan d

Kemudian define x1 = a + d dan x2 = b-d untuk mencari minima : File:If1.jpg File:If2.jpg utuk maxima berkebalikan