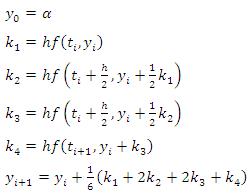Kelompok 4
TUGAS KELOMPOK 4
Bismillahirrahmanirrahim.
Contents
- 1 PERKENALAN
- 2 TUGAS 1: Gauss Jordan dalam Penyelesaian Persamaan Aljabar Linear
- 3 TUGAS 2: Gauss Jordan dalam Penyelesaian Statika Struktur
- 4 TUGAS 3: Runge Kutta
- 5 TUGAS 4: Computational Fluid Dynamic Drag Analysis of a Car
- 6 TUGAS 5: Computational Fluid Dynamic Drag and Lift Analysis of an Airfoil
PERKENALAN
Perkenalkan kami dari kelompok 4 yang beranggotakan:
1. Satria Nur Muhammad
2. Stefanus Nandiwardhana
3. Rafiq Ali Abdillah
TUGAS 1: Gauss Jordan dalam Penyelesaian Persamaan Aljabar Linear
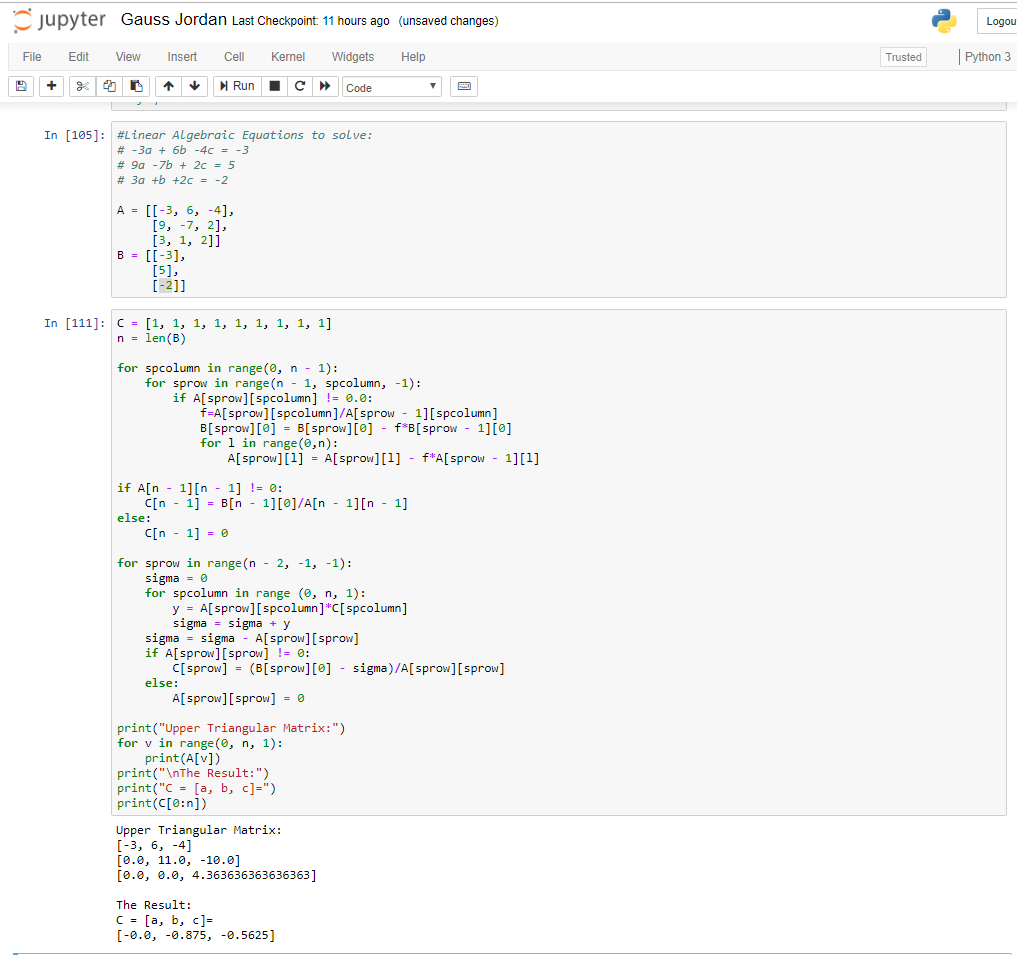
Pada tugas ini kami menyelesaikan suatu persamaan Aljabar Linear dengan metode Gauss Jordan menggunakan python.
TUGAS 2: Gauss Jordan dalam Penyelesaian Statika Struktur
Pada tugas ini kami menyelesaikan suatu persamaan Statika Struktur dengan metode Gauss Jordan menggunakan python.
Kami mengambil contoh soal sebagai berikut:
Sebuah batang panjang 12 m diberi beban 1500N ditengah batang. Lalu kami menghitung support reaction yang terjadi pada dua ujung batang.
#menghitung manual Fx+Fy=1500N 8Fx-12Fy=0 Fx=600N Fy=900N
#menghitung support reaction pada phyton
import numpy as np
a=np.array ([[1,1],
[8,-4]])
b=np.array ([[1500],
[0]])
c=[1,1,1,1,1,1,1,1]
n=len(b)
for k in range(0,n-1):
for i in range(n-1,k,-1):
if a[i][k]!=0.0:
op=a[i][k]/a[i-1][k]
b[i][0]=b[i][0]-op*b[i-1][0]
for f in range (0,n):
a[i][f]=a[i][f]-op*a[i-1][f]
if a[n-1][n-1]!=0:
c[n-1]=b[n-1][0]/a[n-1][n-1]
else:
c[n-1]=0
for i in range(n-2,-1,-1):
sigma=0
for k in range(0,n,1):
y=a[i][k]*c[k]
sigma=sigma+y
sigma=sigma-a[i][i]
if a[i][i]!=0:
c[i]=(b[i][0]-sigma)/a[i][i]
else:
a[i][i]=0
for v in range(0,n,1):
print(a[v])
print(c[0:n])
TUGAS 3: Runge Kutta
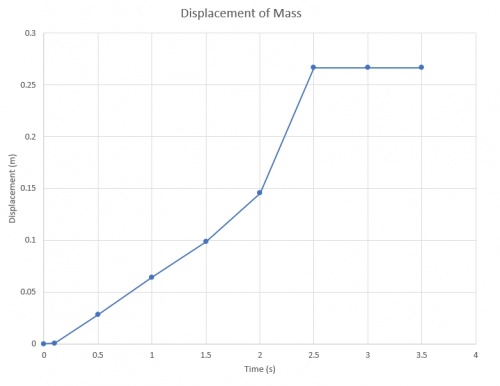
Menyelesaikan sebuah soal dengan methode runge kutta, diberikan sebuah soal pegas dimana prinsip pegas ini biasa digunakan pada kegiatan sehari hari seperti shock breaker dan lain lain. Pada sebuah pegas pasti memiliki titik kelenturan maksimal pada peernya.
2. Algoritma penyelesaian soal
a. dari soal diketahui jika nilai k=75 N/m dan dengan massa 2,5kg
b. jika massa ditarik dengan waktu kurang dari 2 detik maka gaya nya 10t, jika ditarik dalam 2 detik atau lebih maka gayanya 20 N
c. massa tersebut ditarik dengan fungsi P(t)
d. untuk mencari renggangan maka
y=P(t)/m-ky/m
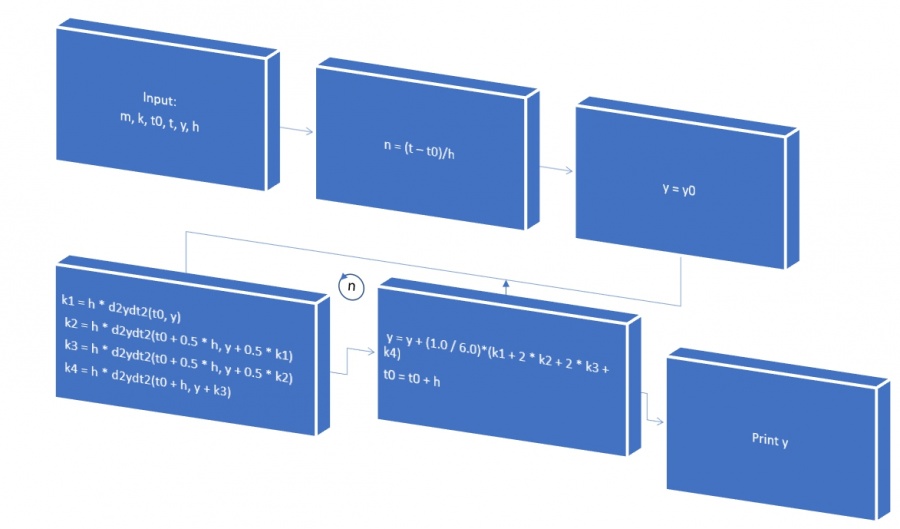
Metode Runge Kutta
Fenomena Fisika
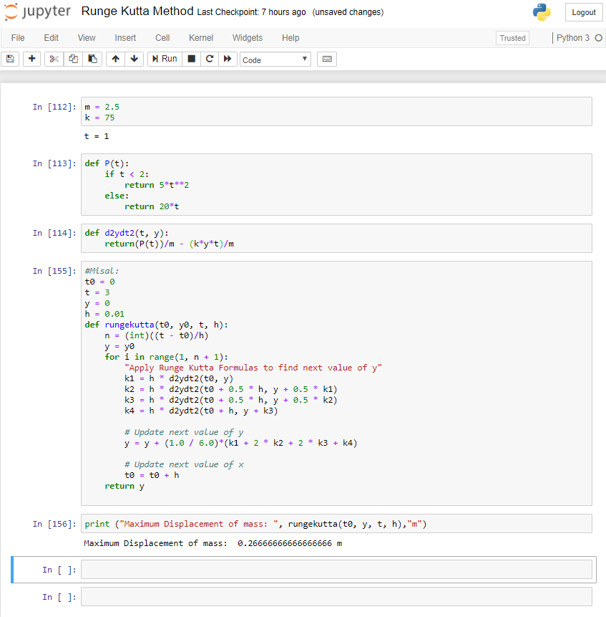
Sebuah benda dengan massa 2.5kg di atas lantai (tanpa gesekan) dikaitkan kepada pegas dengan koefisien pegas 75N/m. Benda tersebut kemudian ditarik dengan arah yang berlawanan dari gaya tarik pegas dengan gaya sebesar 10t N saat t < 2s dan gaya yang sebesar 20N saat t ≥2 s. Gaya tersebut harus melawan gaya tarik pegas. Benda akhirnya mengalami perpindahan dengan percepatan gaya tarik dibagi massanya, dikurangi gaya pegas dikali perpindahan dibagi massa benda.
Program untuk menyelesaikannya
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Mohon masukkan nilai t positif.")
TUGAS 4: Computational Fluid Dynamic Drag Analysis of a Car
Tahap-Tahap Analsis Drag Mobil Analisis Drag Force dimulai dengan menggunakan program CFDSOF. Pada program CFDSOF, dilakukan impor gambar 3D dari mobil yang akan dianalisis, pembuatan mesh, beserta input data dan boundary condition yang diinginkan. Setelah semua data telah diinput, dilakukan penjalanan solver.Analisis dilanjutkan dengan menggunakan program ParaView.
Pada program ParaView, dilakukan penghilangan internalMesh dan dimunculkan car_body.
Setelah itu, dilanjutkan dengan membuat filter "Generate Surface Normal" dengan "Compute cell normal"
Setelah itu, dilakukan perhitungan menggunakan kalkulator yang ada di program dengan menggunakan Attribute Mode Cell Data, mengganti Result Array Name menjadi Drag Force, dan melakukan perhitungan p*Normal_X
Terakhir, tambahkan filter Integrate Variables dan dapatkan nilai Drag Force
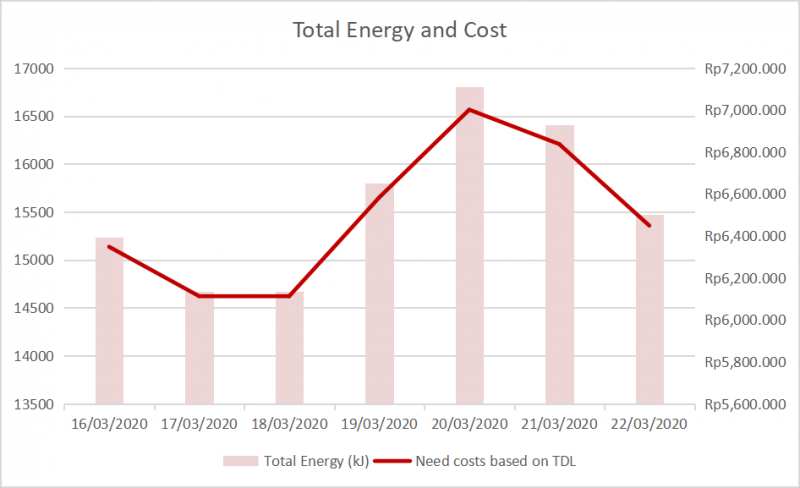
Berikut Hasil yang kami dapatkan:
TUGAS 5: Computational Fluid Dynamic Drag and Lift Analysis of an Airfoil
Langkah-langkah yang digunakan hampir sama seperti tugas drag force mobil, hanya saja ditambah optimasi.
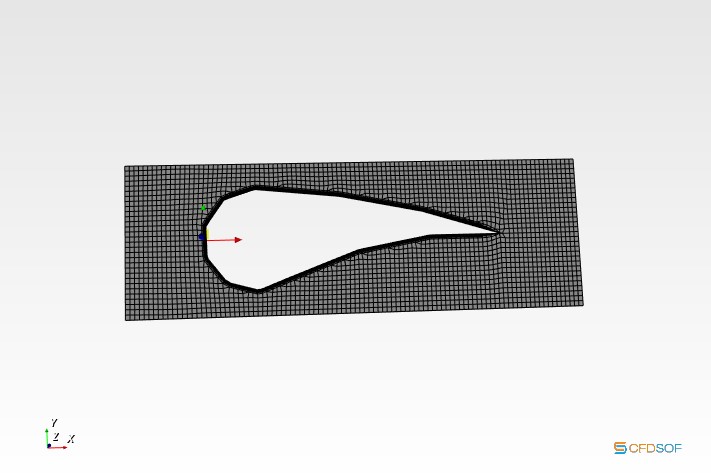
Yang pertama adalah tahap desain airfoil
Yang kedua adalah tahap mesh menggunakan CFDSOF
Yang ketiga adalah tahap simulasi dan kalkulasi menggunakan paraview
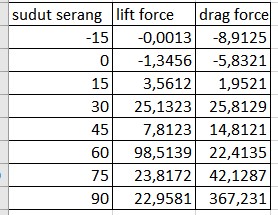
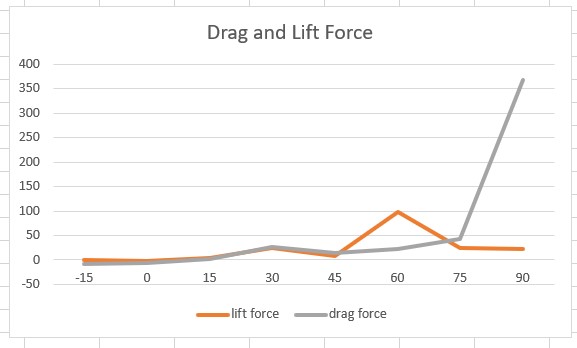
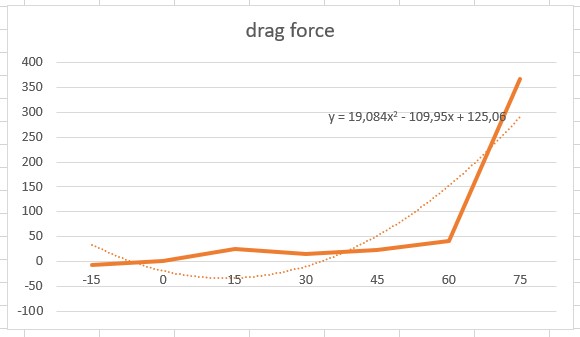
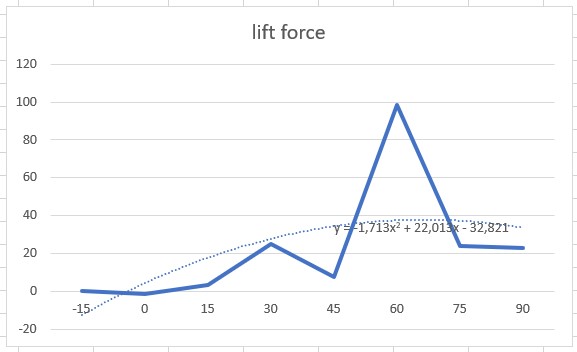
Yang selanjutnya adalah memvariasikan nya terhadap sudut serang -15,15,30,45,60,75,90 derajat.
Hasilnya
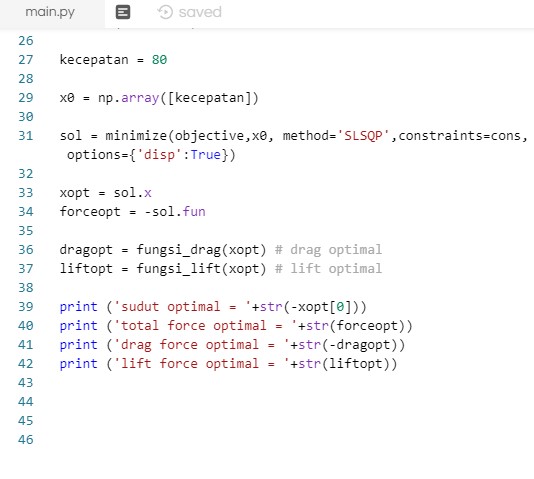
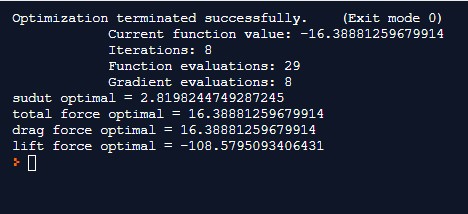
Yang keempat optimasi
Hasilnya adalah sudut serang optimalnya sebesar 2.9 derajat