Kelompok 10
Perkenalkan anggota kelompok 10:
1. Kanwaljot Kaur 1706036305
2. Farhan Tiarrafi Pratama 1806201075
3. Aldy Cahya Ramadhan 1806149040
Eliminasi Gauss
Hari ini kita akan membuat sebuah program tentang gauss elimination yang bertujuan menyelesaikan tugas yang telah diberikan.
Petunjuk Pengerjaan Menggunakan Phyton
Dalam pengerjaan Eliminasi Gauss dengan menggunakan phyton setidaknya ada 3 langkah yang harus diselesaikan terlebih dahulu, tambahan 1 langkah tersebut jika dibandingkan dengan pengerjaan menggunakan matematis adalah pendefinisian matriks. Sehingga secara umum langkah pengerjaan Eliminasi Gauss dengan menggunakan phyton adalah sebagai berikut:
1. Pendefinisian Matriks
Pendefinisian tersebut dibantu dengan menggunakan fungsi array dari numpy dengan cara import numpy.
2. Eliminasi Gauss
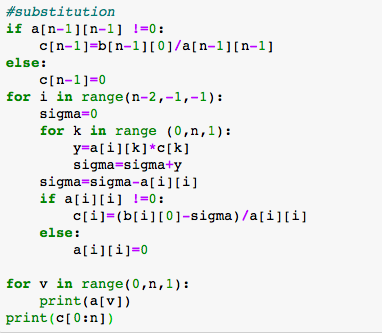
3. Back Substitution
Berikut program python:
Setelah dijalankan, didapatkan hasil sebagai berikut:
Pengaplikasian Eliminasi Gauss: Statika Struktur
Pengaplikasian penghitungan gauss elimination dapat di aplikasikan dalam sebuah perhitungan kasus statika struktur.
Berikut program python:
Setelah dijalankan, didapatkan hasil sebagai berikut:
Tugas: Runge Kutta Method
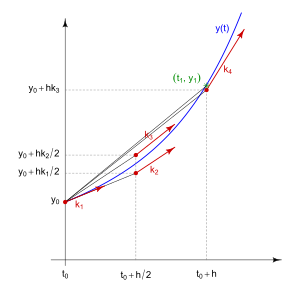
Runge Kutta merupakan metode untuk pendekatan suatu nilai persamaan yaitu dengan melakukan segmentasi-segmentasi dengan suatu garis-garis lurus dari suatu titik ke titik berikutnya mengikuti segmentasi yang dibuat. Runge Kutta terdiri dari beberapa orde, diantanya adalah orde 2, orde 3, dan orde 4. Perbedaan dari beberapa orde tersebut adalah: Runge Kutta Orde 4 lebih akurat dari Orde 3, sedangkan Runge Kutta Orde 3 lebih akurat dari Orde 2.
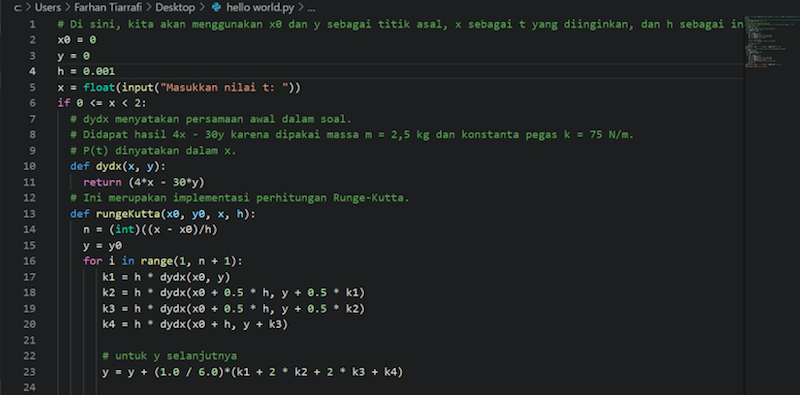
Dalam tugas kali ini kami akan membuat Runge Kutta Orde 4 untuk menyelesaikan suatu permasalahan pegas. Secara umum persamaan Runge Kutta Orde 4 adalah sebagai berikut:
𝑦_(𝑖+1)=𝑦_𝑖+1/6 (𝑘_1+2𝑘_2+2𝑘_3+𝑘_4 )ℎ
Dengan :
𝑘_1=𝑓(𝑥_𝑖,𝑦_𝑖 )
𝑘_2=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_1 ℎ)
𝑘_3=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_2 ℎ)
𝑘_4=𝑓(𝑥_𝑖+1/2 ℎ,𝑦_𝑖+1/2 𝑘_3 ℎ)
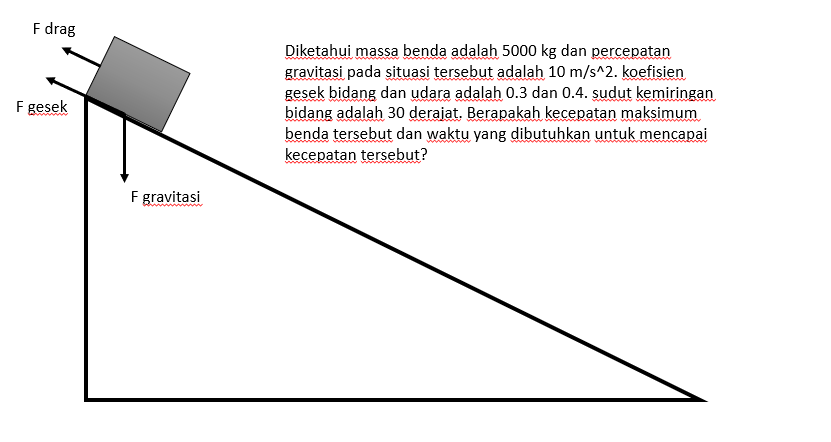
sekarang kita ingin mencoba menyelesaikan sebuah permasalahan dengan metode Runge Kutta :
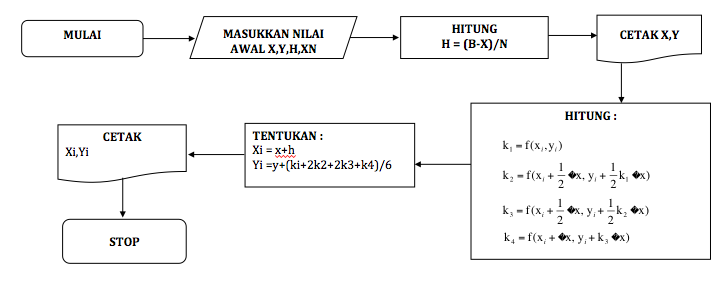
Berikut flowchart untuk menyelesaikan soal tsb:
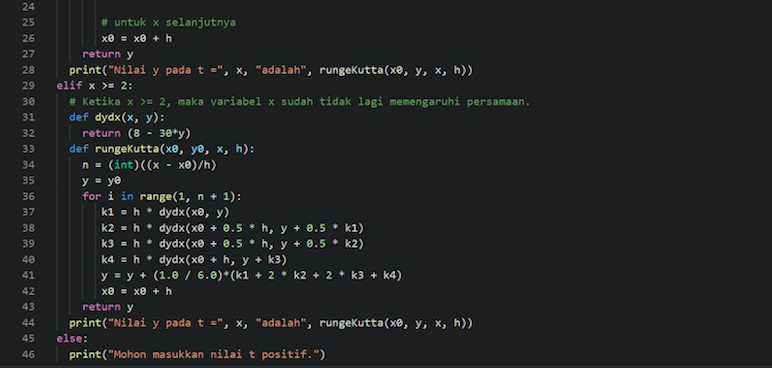
Program untuk python:
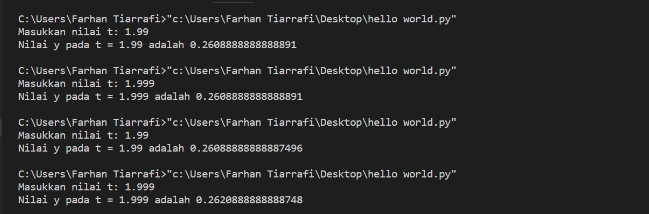
Ketika di jalankan, hasil programnya sebagai berikut: