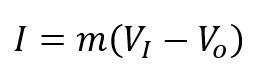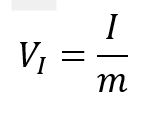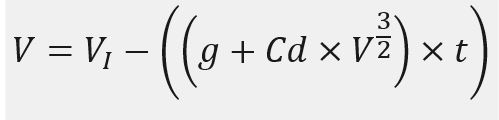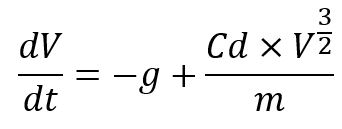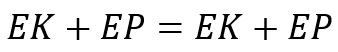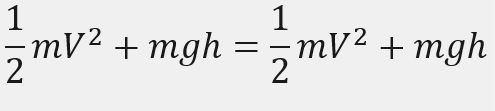Pemodelan Persamaan Gerakan Lemparan Vertikal
Studi Kasus
Persamaan yang ditulis dengan inisial RAU merupakan suatu persamaan mengenai gerakan melempar vertikal keatas, contoh aplikasi yang ada di dunia nyata adalah lemparan genteng keatas dari tukang bangunan.
Video contoh melempar genteng[1]
Model Matematika
Impuls yang diberikan Tukang Bangunan
Perlambatan Kecepatan oleh Gravitasi dan Gaya Drag Udara
Kondisi genteng telah menyentuh tanah kembali
Algoritma
Persamaan ini dapat diselesaikan dengan metode runge kutta, dalam kasus ini saya ingin mencoba mencari waktu untuk mencapai kondisi tertinggi genteng yang dilemparkan keatas tersebut. Cara-cara yang akan saya lakukan adalah sebagai berikut:
1. Menyusun input yang akan digunakan yaitu terdiri dari gaya dorong, nilai gravitasi, koefisien drag,masa genteng, dan area genteng.
2. Membuat pendefinisian dari nilai persamaan sesuai dengan persamaan matematis yang sudah dibuat, pendefinisian berupa suatu persamaan diferensial
3. Untuk mendapatkan nilai waktu maka runge kutta harus dibuat suatu sistem iterasi yaitu dengan menggunakan while, sehingga terjadi iterasi sampai kecepatan 0 dan diperoleh waktunya.
4.
Flowchart
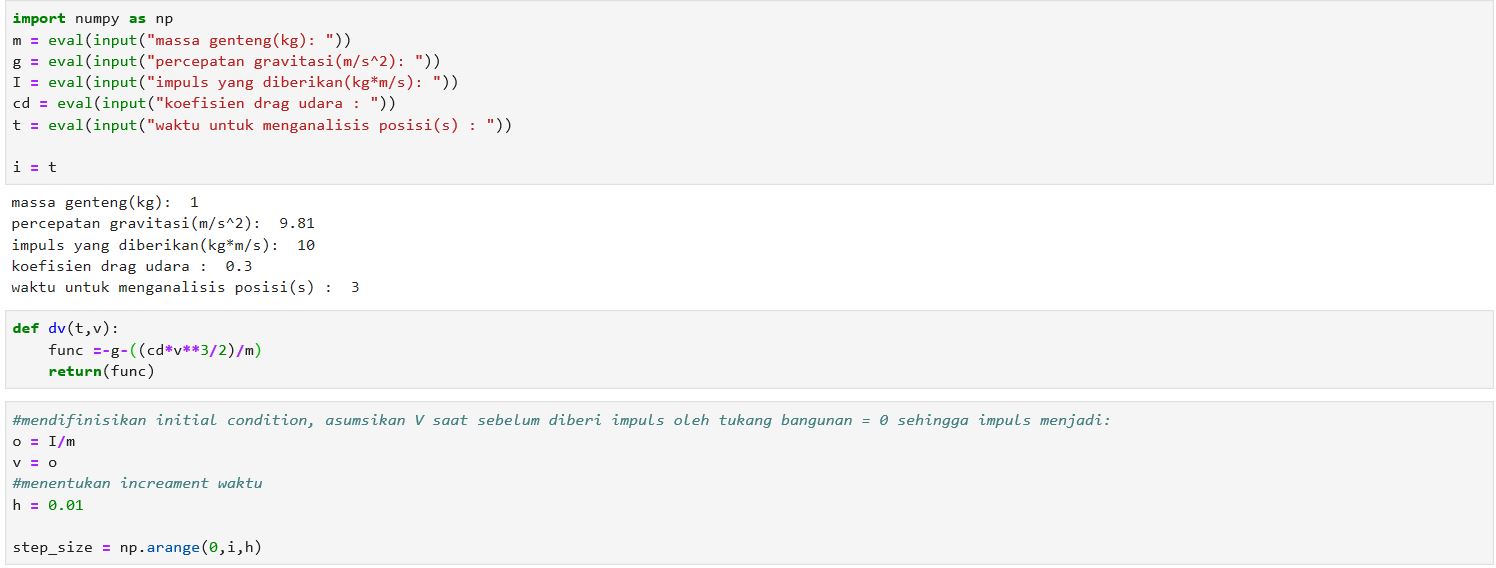
Coding
import numpy as np
m = eval(input("massa genteng(kg): "))
g = eval(input("percepatan gravitasi(m/s^2): "))
I = eval(input("impuls yang diberikan(kg*m/s): "))
cd = eval(input("koefisien drag udara : "))
t = eval(input("waktu untuk menganalisis posisi(s) : "))
i = t
def dv(t,v):
func =-g-((cd*v**3/2)/m)
return(func)
#mendifinisikan initial condition, asumsikan V saat sebelum diberi impuls oleh tukang bangunan = 0 sehingga impuls menjadi: o = I/m v = o #menentukan increament waktu h = 0.01
step_size = np.arange(0,i,h)
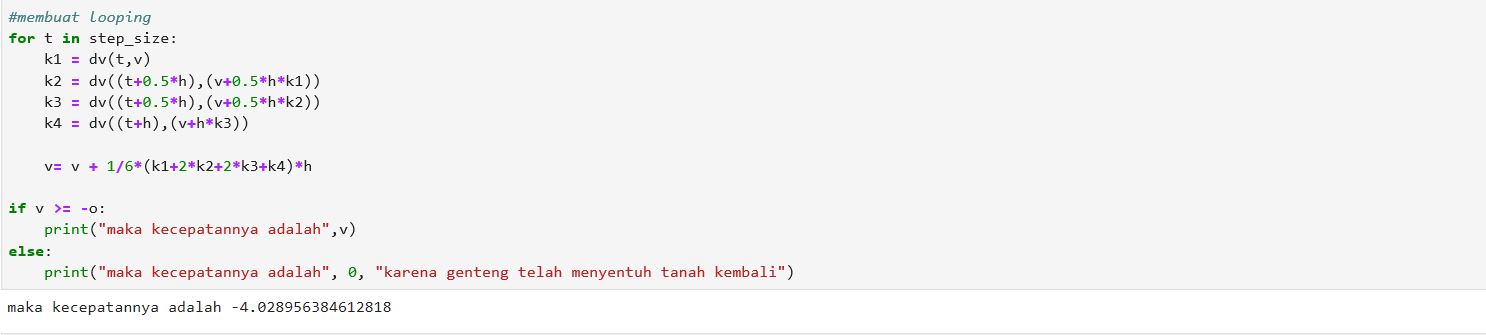
#membuat looping
for t in step_size:
k1 = dv(t,v)
k2 = dv((t+0.5*h),(v+0.5*h*k1))
k3 = dv((t+0.5*h),(v+0.5*h*k2))
k4 = dv((t+h),(v+h*k3))
v= v + 1/6*(k1+2*k2+2*k3+k4)*h
#pendefinisian if dan else berikut ini berdasarkan pada konservasi energi kinetik dan potensial bahwa jumlah energi kinetik dan potensialnya selalu konstan
if v >= -o:
print("maka kecepatannya adalah",v)
else:
print("maka kecepatannya adalah", 0, "karena genteng telah menyentuh tanah kembali")