Skandha M Rajasingam

Profil

Nama: Skandha M Rajasingam

NPM: 1706036532

Jurusan: Teknik Mesin

MEETING 1

METODE NUMERIK Metode Numerik merupakan teknik untuk memformulasikan sebuah rumus matematika agar dapat dipecahkan menggunakan operasi perhitungan biasa. Metode numerik krusial untuk pemecahan permasalahan yang tidak dapat diselesaikan melalu metode exact. Metode numerik dalam bidang computer menjadi fokus dalam bidang pelajaran semester ini. salah satu metode numerik yang dipakai pada pertemuan ini adalah Taylor's Method.

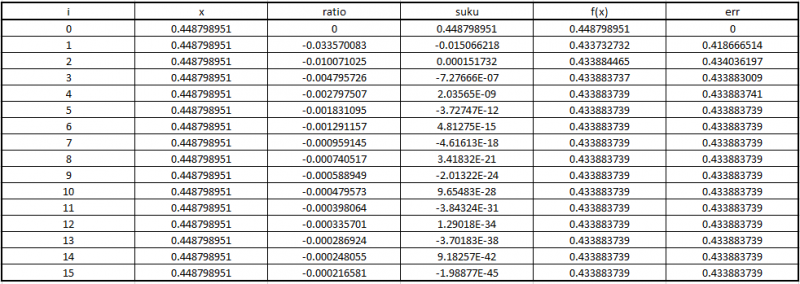
Taylor's Method Taylor's Method merupakan representasi sebuah fungsi sebagai jumlahan tak hingga dari suku suku yang nilainya dihitung dari turunan fungsi tersebut fungsi Utama dari Taylor's Method dalam pembelajaran ini adalah untuk meng aproksimasikan nilai dari sebuah fungsi. dalam kasus ini mengaproksimasikan nilai dari Sin(pi/7).

MEETING 2

BAHASA PEMROGRAMAN Dalam dunia engineering, pemrograman bukanlah sesuatu yang asing. di segala sudut dan bidang engineering kita sudah bisa melihat implementasi dari program computer. Oleh karena itu, pengetahuan tentang berbagai macam Bahasa pemrograman serta aplikasinya dalam dunia kerja adalah sesuatu yang sangat penting di dunia yang modern ini. Pada kesempatan ini, bahasa pemrograman yang kami pelajari adalah C++. alasan kami memilih bahasa pemrograman C++ adalah fleksibilitas bahasa tersebut. Bahasa tersebut kompatibel dengan banyak sistem dan perangkat dari berbagai bidang.

PSEUDO CODE Sebelum kami mulai mempelajari pemrograman C++, kami diberi tugas untuk menulis pseudo-code sebuah program sederhana. Dalam kasus ini program tersebut adalah program Maclaurin Series. Program ini mampu menghitung nilai dari sin(x), cos(x), serta derajat akurasi yang dibutuhkan. pseudo-code dimulai dengan menulis variabel-variabel yang dibutuhkan dalam program tersebut. Langkah kedua adalah dengan menulis parameter yang dibutuhkan,dalam kasus ini parameter yang dibutuhkan ialah error= 1e-7. langkah ke 3 adalah untuk menetapkan rasio yang akan dipakai untuk mencapai nilai yang dibutuhkan. langkah ke 4 adalah untuk menetapkan pertambahan gradual dari suku pertama ke suku selanjutnya. Setelah pseudo-code selesai, kertas dikumpulkan ke dosen kelas.

TUGAS 1: GOVERNING EQUATION

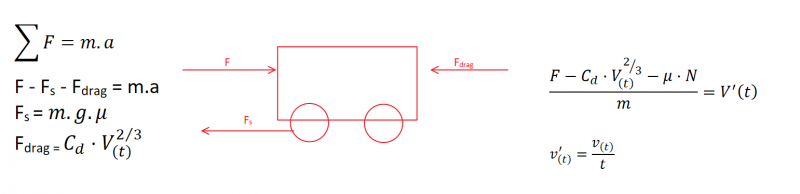
Berikut merupakan governing equation untuk mobil yang sedang bergerak serta gaya yang berlaku pada mobil tersebut.

dari Analisa gaya tersebut program yang kami formulasikan dalam python seperti berikut: import math import cmath

m = float(input("massa mobil: ")) Cd = float(input("Koefisien Drag Udara: ")) Myu = float(input("koefisien gesek dinamis: ")) a = float(input("percepatan mobil: ")) g = float(9.18) #gravitational_acceleration N = float(m*g) #Normal_Force V0 = float(0) #inital_speed_value2 t0 = float(0) #initial time_value H = 1 #step_size Error = float(100) print ("data data runge kutta: ")

def Va(t0, V0):

   return ((m*a)-(Cd*V0**(2/3)-Myu*N)/m)

while(Error>0.0005):

   k1 = Va(t0, V0)
   k2 = Va(t0 + 0.5, V0 + k1*0.5)
   k3 = Va(t0 + 0.5, V0 + k2*0.5)
   k4 = Va(t0 + 1, V0 + k3)
   V1 = V0 + (1/6)*(k1 + 2*k2 + 3*k3 + k4)
   Error = ((V1 - V0) / V1)
   V0 = V1
   t1 = t0 + H
   t0 = t1

   print (V1)

print ("") print ("kecepatan max mobil merupakan: ", V1) print ("waktu ke top speed: ", t0)